алгебра логики. Алгебра логики. Httpinfolike narod rulogic html Алгебра логики

• Название: Httpinfolike narod rulogic html Алгебра логики
• Анкор: алгебра логики
• Дата: 19.07.2022
• Размер: 315.96 Kb.
• Имя файла: Алгебра логики.docx
• Тип: Закон; #633563

http://infolike.narod.ru/logic.html

Алгебра логики

     Логика очень древняя наука. Ещё в античные времена была известна формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения. Например, уже в древности был известен закон исключения третьего. Его содержательная трактовка была такова: «Во время своих странствований Платон был в Египте ИЛИ не был Платон в Египте». В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте - третьего не дано.
    Другой закон логики - закон непротиворечивости. Если сказать: «Во время своих странствий Платон был в Египте И не был Платон в Египте», то очевидно, любое высказывание, имеющее такую форму, всегда будет ложно. Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
    Ещё один закон, известный в древности - закон отрицания: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте».
    Формальная логика основана на “высказываниях”. “Высказывание” - это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит.
    Например: Листва на деревьях опадает осенью. Земля прямоугольная.
    Первое высказывание содержит истинную информацию, а второе - ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.
    Пример предложений, не являющихся высказываниями: Не пейте сырую воду! Кто не хочет быть счастливым?
    Высказывания могут быть и такими: 2>1, Н2О+SO3=H2SO4. Здесь используются языки математических символов и химических формул.
    Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки - это слова, которые подразумевают определённые логические связи между высказываниями. Основные логические связки издавна употребляются не только в научном языке, но и в обыденном, - это “и”, “или”, “не”, “если ... то”, “либо ... либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если ... то” для связи простых высказываний в сложные.
    Высказывания бывают общими, частными и единичными. Общее высказывание начинается со слов: всё, все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.
    Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке.



    В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики.
    Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Но совпадение это только внешнее, так как смысл они имеют совсем иной.
    Логическая 1 означает, что какое-то событие истинно, в противоположность этому логический 0 означает, что высказывание не соответствует истине, т.е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
    В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ.
    1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения аргументов функции, т.е. входные величины, а в правой указывается соответствующее им значение логической функции. Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:



    Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+».
    Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через А простое высказывание «Летом я поеду в деревню», а через В - простое высказывание «Летом я поеду в туристическую поездку». Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
    2. Логическая операция И. Таблица истинности для этой функции имеет вид: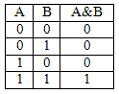



    Из таблицы истинности следует, что операция И - это логическое умножение, которое ничем не отличается от традиционно известного умножения в обычной алгебре. Операцию И можно обозначить знаком по-разному:





    В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
    3. Логическая операция НЕ. Эта операция является специфичной для алгебры логики и не имеет аналога в обычной алгебре. Она обозначается чертой над значением переменной, либо знаком приставки перед значением переменной:



    Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид: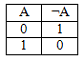



    В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ - дизъюнкцией, операцию И - конъюнкцией. Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
    Логическая операция “строгая дизъюнкция”. Этой логической операции соответствует логическая связка “либо ... либо”. Таблица истинности для этой функции имеет вид:



    Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул:



и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
    Логическая операция “импликация”. Выражение, начинающееся со слов если, когда, коль скоро и продолжающееся словами то, тогда, называется условным высказыванием или операцией «импликация». Таблица истинности для этой функции имеет вид: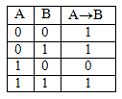



    Операцию “импликация” можно обозначить по-разному:



    Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы





    Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид: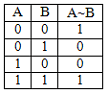



    Операция “эквивалентность” обозначается по-разному. Выражения



обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы



    С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство.



    В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома идемпотентности (отсутствие степеней и коэффициэнтов) и др., в записях которых используются логические переменные, принимающие только два значения - логический ноль и логическая единица. Применение этих законов позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму. Основные аксиомы и законы алгебры логики приведены в таблице:



    Примеры использования основных аксиом и законов: 

Логические элементы

     Современный этап промышленного развития характеризуется тем, что разработчики систем автоматики и вычислительной техники стремятся использовать функциональные модули, выполняющие определённые схемные задачи: логические преобразования, хранение информации и т.д. Конкретный вид электрической схемы, использованной для реализации заданной логической функции, как правило, не имеет существенного значения. Техническое устройство, реализующее логическую функцию, может рассматриваться просто как логический элемент, внутренняя структура которого не конкретизируется.
    На принципиальных и функциональных схемах логический элемент ИЛИ изображается прямоугольником с единицей в левом верхнем углу.



    Логический элемент ИЛИ предназначен для “вычисления” значения логического сложения. Работа этого логического элемента эквивалентна проверке составного условия со служебным словом “или”. Алгоритм работы логического элемента “или” записывается следующим образом: “Если А=1 или В=1, то f(А,В)=1, иначе f(А,В)=0”.
    Логический элемент И предназначен для “вычисления” значения логического умножения. Работа этого логического элемента эквивалентна проверке составного условия со служебным словом “и”. Алгоритм работы логического элемента “и” записывается следующим образом: “Если А=1 и В=1, то f(А,В)=1, иначе f(А,В)=0”.
    Изображение логических элементов И на функциональных и принципиальных схемах выглядит так: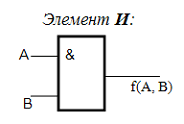



    Логические элементы НЕ изображаются с кружком, который называется индикатором уровня сигнала.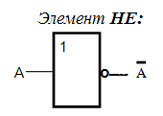





    Итак, нам известны три основных логических элемента И, ИЛИ, НЕ. Сигналы, вырабатываемые одним логическим элементом, можно подавать на вход другого элемента - это даёт возможность образовывать цепочки из отдельных логических элементов.
    Например: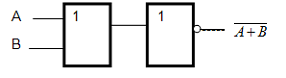



    Каждую такую цепочку называют логическим устройством, а соответствующую схему - функциональной схемой. Функциональную схему, которую полностью можно описать таблицей истинности, называют комбинационной схемой.
     Комбинационная схема - это схема, в которой значения входных переменных в текущий момент времени полностью определяют значения выходных переменных.
    Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, и более сложных элементов И-НЕ, ИЛИ-НЕ и др., соединяя их так, как это следует из логической функции. Рассмотрим элементы И-НЕ и ИЛИ-НЕ: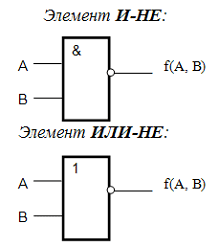



    Логическая функция И-НЕ, которая представляет собой отрицание логического умножения, называется операцией Шеффера и кратко может быть записана в следующем виде:



    Логическая функция ИЛИ-НЕ, т.е. отрицание логического сложения, носит название «стрелка Пирса» и обозначается так:



    Связь операций И-НЕ и ИЛИ-НЕ с основными операциями алгебры логики устанавливается законами, открытыми английским математиком Августусом де Морганом (1806-1871) и поэтому носящими его имя. Первый из них устанавливает, что отрицание логического умножения равносильно сумме отрицаний сомножителей:



    Второй закон показывает, что отрицание логического сложения равносильно произведению отрицаний слагаемых:



    Законы де Моргана сведены в таблицу законов алгебры логики.

Построение комбинационных схем

    Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др., нами не рассмотренных. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.
    Двигаясь от начала схемы, на входе каждого элемента записывается буквенное выражение входного сигнала. Входы подаются на условное обозначение логических элементов, на выходе которых записывается логическая формула начала обработки входных сигналов, а затем их выходы соединяются так, как указано в заданной логической функции, и на выходе всей комбинационной схемы записывается выражение выполненной логической функции.
    Пример: Пусть дана логическая функция



    Требуется составить комбинационную схему.
    Прежде чем перейдём к рисованию схемы, полезно выяснить следующие вопросы:
    

 Какие операции используются в логической функции?
    

 Как заданные операции условно обозначаются?
    

 Каков порядок выполнения операций?

    Ответив на все эти вопросы, не составит большого труда нарисовать комбинационную схему: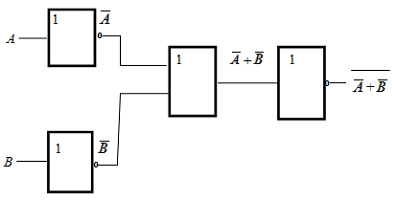



    Другой класс логических схем составляют схемы с внутренней памятью. Такие схемы называют последовательностными. Только анализируя логические схемы можно понять, как работает то или иное логическое устройство

Арифметико-логическое устройство

    Арифметико-логическое устройство (АЛУ) является узлом ЭВМ, который выполняет арифметические и логические операции над данными, обрабатываемыми ЭВМ. Основной элемент, используемый в АЛУ, называется полусумматором. Функция полусумматора заключается в сложении двух двоичных цифр, в результате чего образуется сумма (S) и перенос в старший разряд (Р) в соответствии с правилами двоичного сложения. Вспомните таблицу сложения двоичных чисел:

0+0=0 0+1=1 1+0=1 1+1=10
    Таблица результата работы полусумматора:



    Условно полусумматор на логических схемах изображается следующим образом:



    Очевидно, что полусумматор имеет два входа А и В и два выхода S и Р. Первый столбец результата этой таблицы аналогичен логической операции И, он даёт перенос из данного разряда в следующий. Столбец S даёт значение младшего разряда суммы двух чисел и представляет собой логическую операцию “сложение по модулю 2”. Эта операция эквивалентна арифметическому сложению двух бинарных чисел.
    Таблице истинности результата работы полусумматора в аналитической форме соответствуют следующие записи логических функций: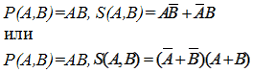



    Практическая реализация такого устройства не составит особого труда, так как построение комбинационных схем по логическим функциям уже рассматривалось ранее. Каждая из схем полученных пар записей логических функций будет иметь по 6 логических элементов: 5 для получения значения S и ещё один для формирования сигнала переноса Р. Однако во второй паре функций выражение для значения S можно преобразовать, воспользовавшись вторым законом де Моргана:





    Отсюда видно, что для реализации полусумматора будет достаточно четырёх логических элементов: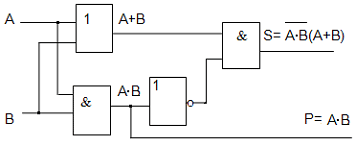



    На данном примере изображена комбинационная схема простейшего «полусумматора», устройства для сложения двух бинарных чисел А и В, где S - результат сложения, а Р - перенос в старший разряд. Рассматриваемому устройству дано название “полусумматор” потому, что оно хотя и даёт значение суммы двух величин и переноса в следующий разряд, однако не учитывает сигнал переноса, получаемый в предыдущем (младшем) разряде. Для получения полного двоичного одноразрядного сумматора необходимы два полусумматора. Следовательно, двоичный одноразрядный сумматор должен иметь три входа и два выхода. На логических схемах он условно изображается так: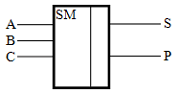



    На входы А и В подаются соответственно цифры первого и второго слагаемого, а на вход С - цифра переноса из предыдущего разряда. Выходы S и Р так же, как в полусумматоре, соответственно выводят значения суммы и переноса в следующий разряд.
    Комбинируя полусумматоры и двоичные одноразрядные сумматоры можно составить сумматор для сложения n-разрядных двоичных чисел. Приведём в качестве примера условную схему так называемого двоичного четырёхразрядного сумматора: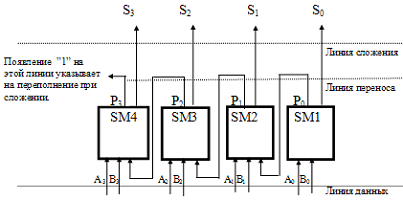



    Двоичные n-разрядные сумматоры имеют существенный недостаток - малое быстродействие из-за значительного времени распространения переноса: чем больше разрядность складываемых чисел, тем больше время задержки работы устройства. Инженеры схемным путём добиваются увеличения быстродействия работы сумматора, сокращая время распространения переноса, тем самым увеличивая скорость работы АЛУ.

Моделирование памяти. Триггер

    Все рассмотренные ранее логические устройства только преобразовывали информацию, представленную в виде нулей и единиц. Однако, можно научить логическое устройство запоминать информацию, хранить и вспоминать её при необходимости. Такому устройству дали название триггер. Существует много разновидностей триггеров в зависимости от комбинации сигналов, управляющих их переключением. Мы рассмотрим лишь три из них: Т-триггер, RS-триггер и D-триггер.
    Рассмотрим диаграмму работы Т-триггера: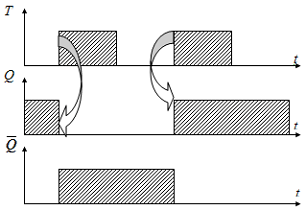





    Состояние выхода Т-триггера меняется на противоположное при поступлении на его вход счётного сигнала Т=1 и сохраняется неизменным при Т=0. Следовательно, Т-триггер имеет два устойчивых режима выходных сигналов:



    Эти два режима для всех видов триггеров называются состояниями. Режим, когда истинный выходной сигнал равен 1, называется состоянием установки, а второе (когда он равен 0) - состоянием сброса. Говорят, что триггер установлен, если он приведён в состояние установки, и сброшен, если он приведён в состояние сброса. Состояние Т-триггера меняется, если на его единственный вход подаётся “1”.
    RS-триггер имеет два управляющих входа R и S, на которые подаются сигналы установки S и сброса R:



    Таким образом, триггер оказывается в состоянии установки, если S=1 и R=0, и в состоянии сброса, если S=0 и R=1. При S=0 и R=0 триггер работает в режиме хранения, т.е. сохраняет ранее установленное состояние. Комбинация входных переменных S=1 и R=1 (установка и сброс одновременно) является запрещённой, так как может привести к неопределённому (непредсказуемому) состоянию выхода. Во избежание возникновения сбоев эту комбинацию исключают, поэтому она является нереализуемой.
    Логическая схема RS-триггера выглядит так: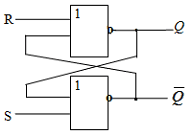




    D-триггер моделирует память точнее всего. Он имеет только один входной сигнал, и его состояние определяется этим сигналом.



    D-триггер переводится в состояние сброса, если на его входе логический 0, и в состояние установки, если на его входе логическая 1.
    Итак, теперь вполне ясно, как в ЭВМ можно записать, сохранить и сбросить бит информации. То, что информацию компьютер хранит в байтах, а 1 байт составляют 8 бит, вы уже знаете. Следовательно, объединяя триггеры в группы (регистры), можно записывать, хранить и сбрасывать и большие объёмы информации.
    Рассмотрим регистр, состоящий из трёх Т-триггеров. Он предназначен для запоминания и демонстрации трёх бит информации. Назовём его простейшим запоминающим устройством (ЗУ):



    Пусть все три триггера установлены в “0” (Х1=Х2=Х3=0). Это значит, что ЗУ помнит и демонстрирует на выходах информацию вида “000”. Подадим на вход первого триггера “1” (Т1=1), тогда выходная информация изменит своё значение - “100”. Следовательно, можно одну информацию заменить другой и хранить её необходимое время, как бы уничтожив предыдущие значения из памяти.
    Оперативная память часто конструируется в виде большого набора регистров, где, как правило, один регистр образует одну ячейку памяти, и каждая ячейка имеет свой номер.
    Таким образом, компьютер - это комплекс различных технических устройств, предназначенных для решения информационно-логических и вычислительных задач, хранения и выдачи больших объёмов информации, а схемное проектирование их является одной из стадий изготовления этой неотъемлемой теперь части нашей жизни.

Вопросы и упражнения

1. В чём различия между формальной логикой и алгеброй логики?
2. Назовите основные операции алгебры логики и их свойства.
3. Какие законы математики используются в алгебре логики?
4. Определите предложения, являющиеся высказываниями:

5. Определите, какие из высказываний являются частными, общими или единичными:
а) Все рыбы умеют плавать.
б) Буква Б – согласная.
в) Некоторые медведи – бурые.

6. Из двух простых высказываний постройте сложное высказывание, используя логические связки «и», «или»:
а) В кабинете есть парты. В кабинете есть стулья.
б) Одна половина класса изучает английский язык. Вторая половина изучает французский язык.
в) Антон старше Лили. Сережа старше Лили.

7. Вычислите значение логического выражения при следующих значениях логических величин А, В и С: А=Истина, В=Ложь, С=Ложь:
а)А или В; б)А и В; в)В или С.

8. Вычислите значение логического выражения при следующих значениях логических величин X, Y и Z: X=Истина, Y=Истина, Z=Ложь:
а)не X и Y; б)X или не Y; в)X или Y и Z.

9. Вычислите значение логического выражения при следующих значениях логических величин А, В и С: А=Истина, В=Ложь, С=Ложь:
а) А или не (А и В) или С; б) не А или А и (В или С); в) (А или В и не С) и С.

10. Определите тип высказывания и вид логической операции с соответствующей логической связкой:
a) Всякий прямоугольник имеет прямые углы и параллельные противоположные стороны;
б) Треугольники с равными сторонами не являются равнобедренными;
в) На следующем уроке будет либо история, либо химия;
г) Завтра я пойду в школу и библиотеку;
д) Либо он заболел, либо забыл о нашей договорённости;
е) Утром мы обычно ходим на лыжах или катаемся на коньках.



11. Используя логические операции, запишите высказывания в виде логических выражений: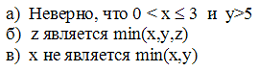

12. Как будет выглядеть логическое выражение, которое опишет интервал



13. Запишите в виде логической формулы высказывания:
а) Число является простым, если оно делится только на единицу и само на себя.
б) Спортсмен подлежит дисквалификации, если он некорректно ведёт себя по отношению к сопернику или судье или принимал «допинг».

14. Укажите ошибку в записи одного из трёх тождеств, приведите правильную запись тождества:



15. В нарушении правил обмена валюты подозреваются четыре работника банка А, В, С и D. Известно, что:
а) если А нарушил, то и В нарушил;
б) если В нарушил, то и С нарушил или А не нарушал;
в) если D не нарушил, то А нарушил, а С не нарушал;
г) если D нарушил, то А нарушил

16. В каких магазинах организована распродажа, если истинны два высказывания: «Неверно, что если магазин А организует распродажу, то и С тоже» и «Из двух магазинов В и С организует распродажу только один».

17. Какие фирмы организуют выставки, если истинны два высказывания: «Фирма А организует выставку, а фирма С не организует» и «Если фирма В организует, то фирма С тоже организует».

18. Упростите логические функции: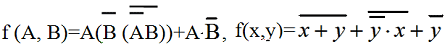



19. Какое устройство описывается функциональной схемой?
20. Дайте определения логического элемента и логического устройства.
21. Назовите основные логические элементы и их свойства.
22. Перечислите классы логических схем.
23. Нарисуйте комбинационные схемы для логических функций



24. Дайте определение арифметико-логическому устройству.
25. Расскажите принцип работы полусумматора.
26. Расскажите принцип работы двоичного одноразрядного сумматора.
27. Как называется устройство, предназначенное для хранения 1 бита информации?
28. Расскажите процесс работы RS-триггера по логической схеме при S=1 и R=0, и S=0 и R=1. Какие состояния принимает RS-триггер в этих случаях?
29. Сколько триггеров понадобится для хранения в памяти слова “информатика”?
30. Сколько триггеров необходимо для реализации 1 ячейки памяти?