Статистический анализ данных. Статистический анализ данных о качестве общеобразовательной подг. Информационный ресурс Статистический анализ данных о качестве общеобразовательной подготовки обучающихся
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Информационный ресурс Статистический анализ данных о качестве общеобразовательной подготовки обучающихся Приводятся алгоритмы статистической обработки матриц результатов тестирования. Показано применение методов описательной статистики с помощью табличного редактора EXCEL. Подробно описаны последовательности действий для вычисления статистических показателей качества подготовки обучающихся, построения таблиц и диаграмм в EXCEL. Полученная в результате статистической обработки информация может быть использована в аналитических отчетах, справках и записках по итогам контроля. Допустим, что число испытуемых равно n. Номер испытуемого обозначается символом i. Число выполняемых испытуемыми заданий N. Номер задания обозначается символом j. Результаты тестирования представляются в виде электронной таблицы (матрицы), в строках которых показаны результаты выполнения заданий каждым испытуемым. Последовательность единиц и нулей в строке называется профилем испытуемого. В столбцах матрицы результатов показаны результаты выполнения каждого задания всеми испытуемыми. Последовательность единиц и нулей в столбце называется профилем задания. В ячейках на пересечении строки (i) и столбца (j) размещается результат выполнения i-м испытуемым j-го задания (xij). В «классической» теории тестировании xij может принимать одно из двух значений: 1, если задание было выполнено; 0, если ответ тестируемого не совпал с эталонным или совпал частично.Для примера рассмотрим модельную таблицу, в которой показаны результаты выполнения 10 испытуемыми (всего n испытуемых) 10 заданий (всего N заданий) (см. таблицу 1). В практике число испытуемых и число заданий, как правило, больше. Следует отметить, что такой объем выборки (10 человек) недостаточен для получения оценок с достаточной точностью и, следовательно, достоверностью; при этом действует известная статистическая закономерность: чем больше объем выборки, тем меньше погрешность оценки. Поэтому представленную таблицу следует рассматривать лишь как модельную, на которой будут демонстрироваться методы и алгоритмы описательной статистики.Таблица 1Матрица результатов тестирования
Обработка результатов, представленных в матрице тестирования, осуществляется по двум «направлениям» – по строкам для оценки успешности выполнения теста каждым испытуемым; по столбцам – для оценки характеристики заданий и теста в целом. Индивидуальные результаты тестирования Анализ «профиля» испытуемого Анализируя последовательность единиц и нулей в профиле испытуемого, можно выделить задания, с которыми он справился, и, следовательно, сделать вывод о сформированности проверяемого знания или умения, а также выделить те задания, с которыми испытуемый не справился, и найти причину невыполнения задания. Расчет сырого тестового балла Суммирование единиц в строке матрицы дает сырой тестовый балл испытуемого xi. Он рассчитывается по формуле 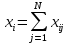 (1) (1)Для вычисления сырого тестового балла в EXCEL необходимо выполнить следующие действия. Навести курсор на ячейку, в которой разместится сумма единиц по строке (рис. 1) 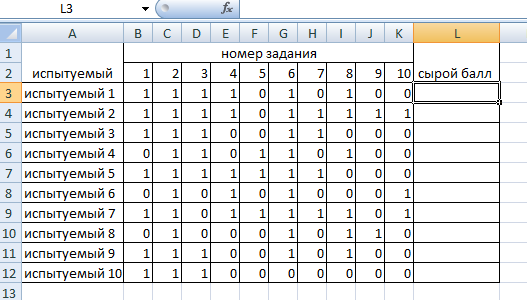 Рис. 1. Выбор ячейки для подсчета суммы баллов по строке Нажать кнопку «автосумма» Ʃ (рис. 2.) 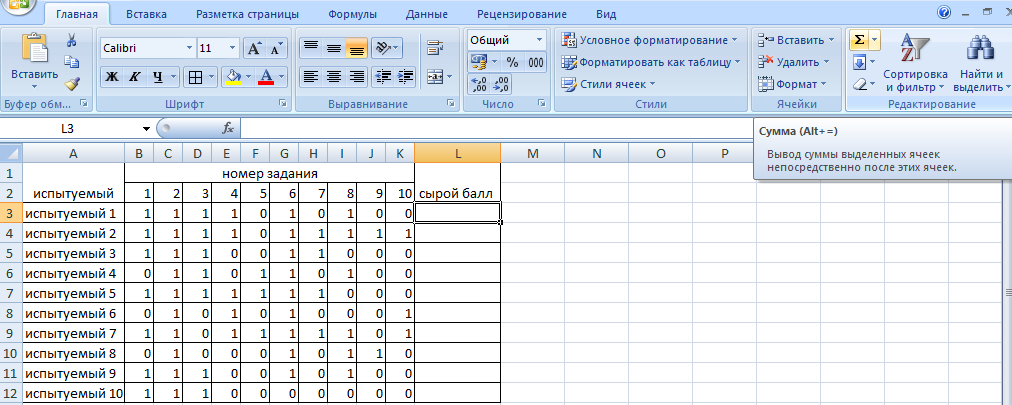 Рис. 2. Выбор автосуммы Выполнить действие (рис. 3). 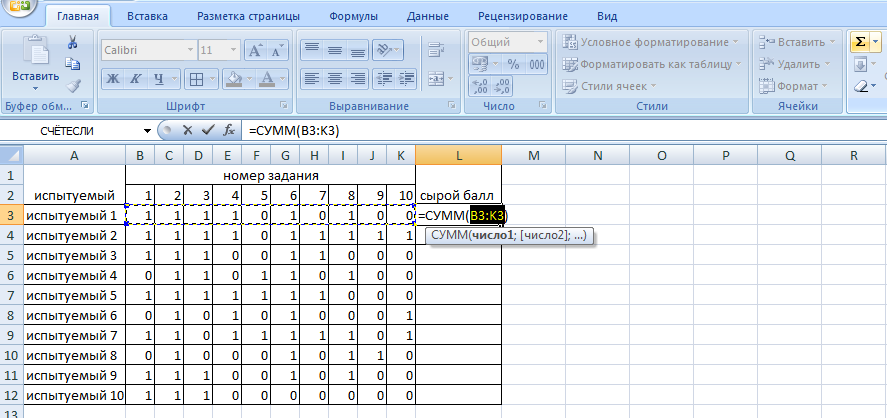 Рис. 3. Подсчет суммы Скопировать содержимое ячейки с полученной суммой на другие ячейки вниз. Так будет рассчитан сырой тестовый балл для каждого испытуемого (рис. 4). 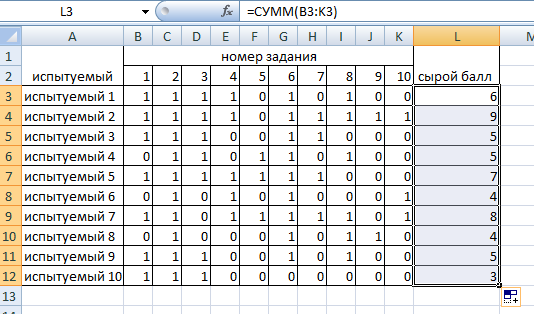 Рис. 4. Копирование содержимого ячейки на весь диапазон Расчет относительного тестового балла Результаты тестирования приходится сравнивать между собой. Но поскольку различные тесты, отображающие содержание и структуру даже одного и того же учебного материала, могут содержать разное число заданий, то простое сопоставление первичных баллов оказывается бессмысленным. В этом случае от абсолютных показателей (сырой тестовый балл) переходят к относительным показателям. Для расчета относительного тестового балла используется формула: 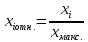 , (2) , (2)где xмакс. – максимально возможный балл за выполнение всех заданий теста. В приведенном примере максимально возможный балл равен числу заданий (10). При использовании политомической шкалы для оценивания результатов выполнения заданий максимально возможный балл рассчитывается с учетом максимального балла за каждое задание. Например, если в тесте 10 заданий на «1» балл и 4 задания на «2» балла, то максимально возможный балл за тест составит 10+4*2=18. Для вычисления относительного тестового балла в EXCEL необходимо выполнить следующие действия. Активировать ячейку рядом с сырым тестовым баллом для испытуемого 1, внести в ячейку формулу и нажать ENTER (рис. 5). 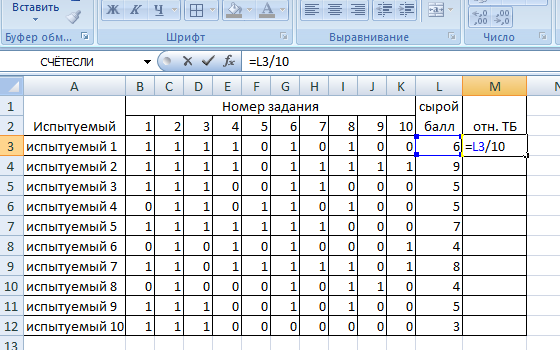 Рис. 5. Запись формулы для подсчета доли Полученное значение скопировать на ячейки вниз (для всех испытуемых) (рис. 6). 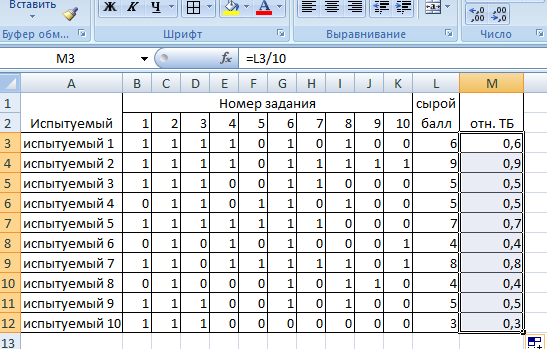 Рис. 6. Копирование содержимого ячейки на весь диапазон При необходимости можно изменить формат ячеек на процентный (рис. 7). 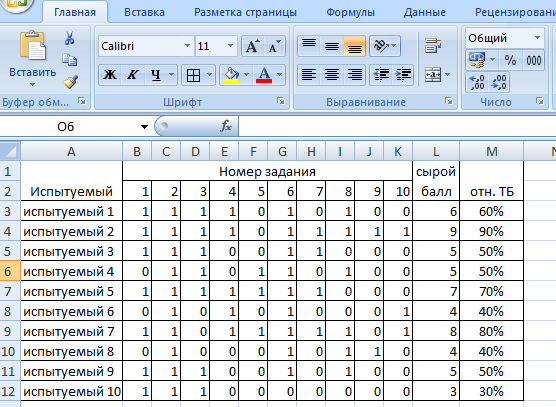 Рис. 7. Изменение формата ячеек на процентный Итоги тестирования, полученные в виде сырых и относительных баллов также могут быть наглядно представлены на гистограмме (один из простых статистических методов контроля и управления качеством). Для построения простой гистограммы с представлением результатов по каждому испытуемому необходимо выполнить следующие действия в EXCEL. Удерживая кнопку Ctrl, выделить столбец с испытуемыми и относительными тестовыми баллами (рис. 8). 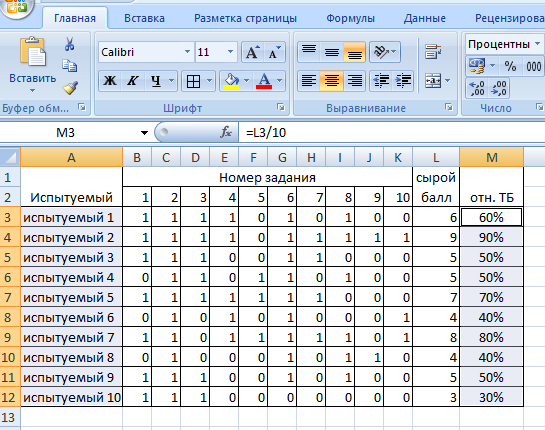 Рис. 8. Выбор диапазона данных для построения гистограммы Нажать кнопку ВСТАВКА, выбрать гистограмму с группировкой. Нажать ENTER (рис. 9). 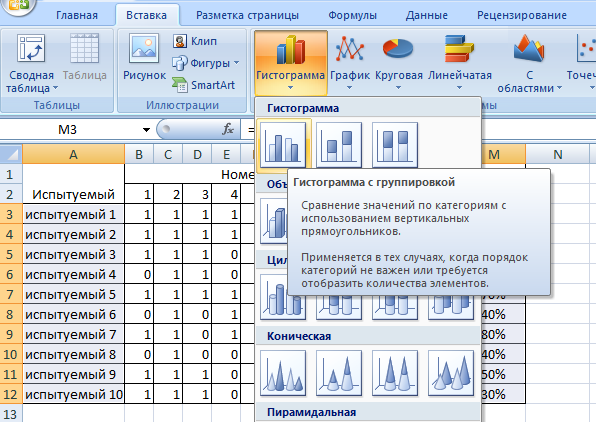 Рис. 9. Выбор типа гистограммы Используя мастер диаграмм, привести гистограмму к необходимому виду (рис. 61). 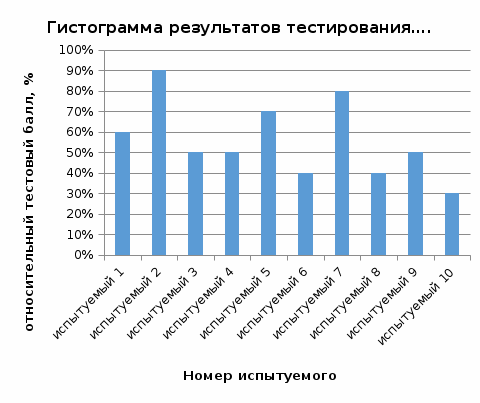 Рис. 10. Гистограмма распределения индивидуальных результатов Анализ групповых результатов тестирования Построение рядов распределения тестовых баллов Несгруппированный частотный ряд распределения На основе ряда индивидуальных сырых тестовых баллов может быть построено частотное распределение результатов тестирования по группе (классу, школе). Для этого необходимо подсчитать, как часто встречается в ряду сырых баллов тот или иной сырой тестовый балл. Неповторяющиеся значения ряда называют вариантами ряда. Для построения частотного ряда распределения сырых баллов выполняются следующие действия. Выписать варианты ряда в столбец. Воспользоваться функцией СЧЁТЕСЛИ. В данном случае можно использовать абсолютную ссылку на анализируемый ряд сырых баллов (рис. 11, 12). 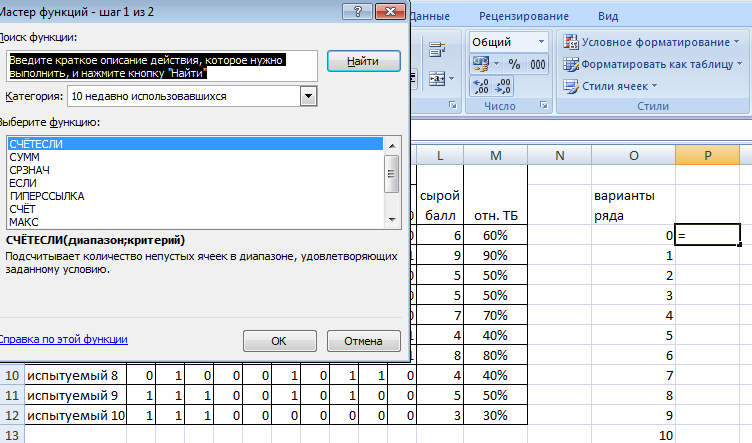 Рис. 11. Запись вариант ряда (неповторяющихся значений) 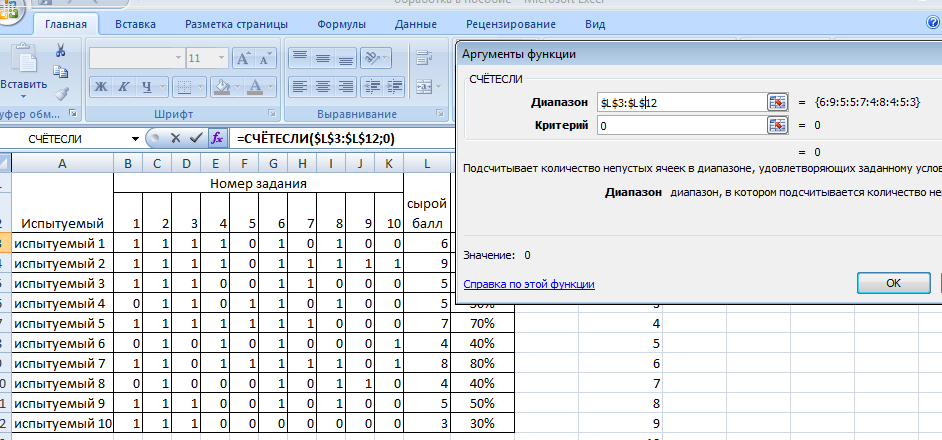 Рис. 12. Абсолютная ссылка на диапазон показана ниже. Скопировать ячейку с полученным значением частоты на другие варианты ряда и заменить критерии (рис. 13). 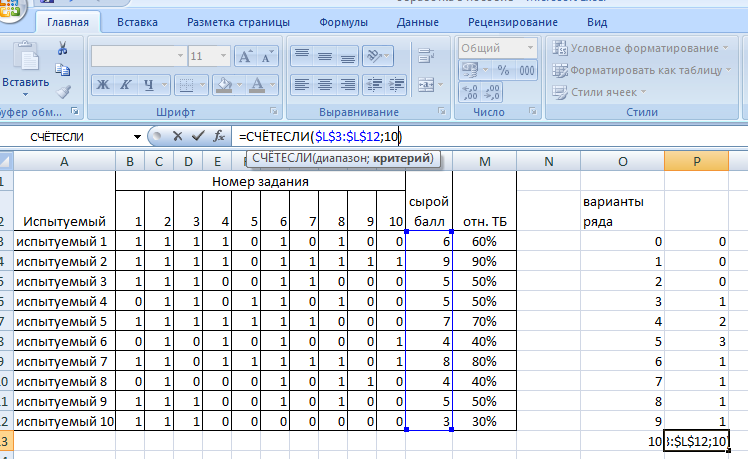 Рис. 13. Функция «счетесли». Копирование ячейки с формулой на весь диапазон В результате получится следующий несгруппированный частотный ряд. Если полученные частоты поделить на число испытуемых, получим частости (или %). Таблица 2 Нгегруппированный частотный ряд
Несгруппированный частотный ряд распределения для наглядности представляют с помощью гистограммы. Для этого нужно воспользоваться мастером диаграмм (рис. 14). 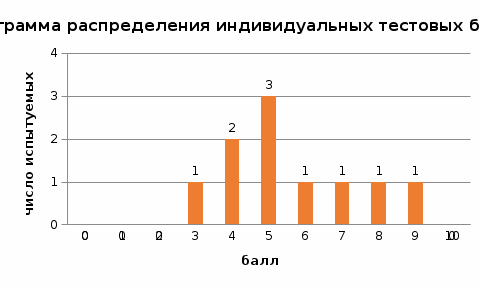 Рис. 14. Вид несгруппированного частотного ряда распределения Гистограмма распределения индивидуальных баллов может быть построена по долям или процентам разных значений в ряду (рис. 66). 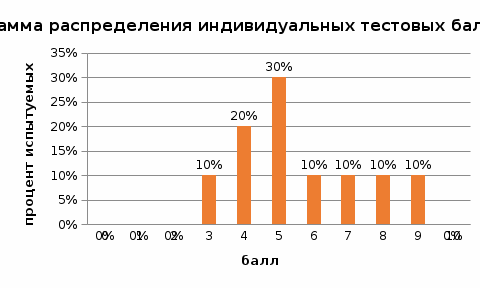 Рис. 15. Вид несгруппированного частотного ряда с долями (процентами) Сгруппированный частотный ряд распределения Если количество вариант ряда (неповторяющихся значений) большое, то может быть построен сгруппированный ряд распределения. Для построения сгруппированного ряда необходимо определить число интервалов (групп) и шаг разбиения. Для расчета числа интервалов используют формулу Стерджеса 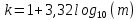 (3) (3)Где m – число вариант ряда. В приведенном примере m=11. Тогда число групп, на которое может быть разбит ряд распределения, равно 5. Для определения шага разбиения нужно размах (разность между максимальным и минимальным значениями в ряду) поделить на число групп. В приведенном примере шаг равен 2 (см. таблицу 3). Таблица 3 Данные для построения гистограммы
Сгруппированный ряд распределения показан на гистограмме ниже (рис. 16). 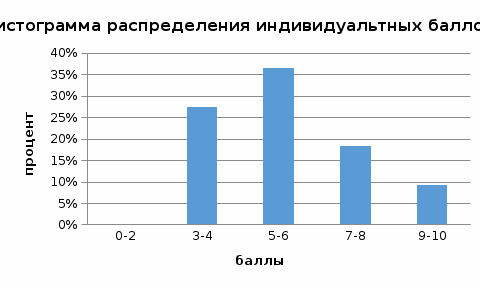 Рис. 16. Вид сгруппированного ряда распределения на гистограмме По виду гистограмм распределения индивидуальных тестовых баллов можно сделать вывод о том, был ли тест легким для данной группы испытуемых, или трудным. Для «легкого» теста характерно смещение распределения вправо (чаще встречаются более высокие баллы). Для «трудного» теста распределение смещено влево, так как чаще встречаются низкие значения индивидуальных тестовых баллов. Смещение распределения может быть связано с завышением оценок при проверке результатов выполнения теста (смещение вправо), или с занижением оценок (смещение влево). Перевод относительного тестового балла в другие шкалы Относительный тестовый балл может быть использован для перевода результативного показателя в другие шкалы. Для этого может быть использована универсальная вербально-числовая шкала качества Харрингтона. Шкала отражает степень выраженности измеряемого и оцениваемого показателя. В случае с результатами выполнения теста степень выраженности качества подготовки обучающегося может быть косвенно оценена долей выполненных заданий в тесте или относительным тестовым баллом. Шкала школьных отметок является порядковой (качественная неметрическая) – для нее определен порядок следования градаций, но не определена разница (интервал) между градациями. Для перевода значений относительных тестовых баллов в пятибалльную шкалу школьных отметок можно воспользоваться следующей таблицей с градациями шкалы Харрингтона. Соответствие шкал тестовых баллов и шкалы школьных отметок
В практике тестирования универсальным является преобразование через установленное (преподавателем, тестовой документацией) соответствие баллов или долей правильных ответов выполнения теста и отметок (баллов). Важно, чтобы оно было единым для всех испытуемых в пределах данного теста (но, очевидно, может отличаться для других тестов). Примером этому могут быть рекомендации по переводу сырого тестового балла в шкалу школьных отметок в контрольно-измерительных материалах для проведения ЕГЭ, ОГЭ, Всероссийских проверочных работ. Следуя указаниям выше, по переведенным в школьные отметки баллам также можно построить частотный ряд распределения и гистограмму с группировкой. Таблица 7со значениями ряда, частотой и частостью, а также гистограмма (рис. 17) показаны ниже. Таблица 4 Распределение испытуемых по отметкам в пятибалльной шкале.
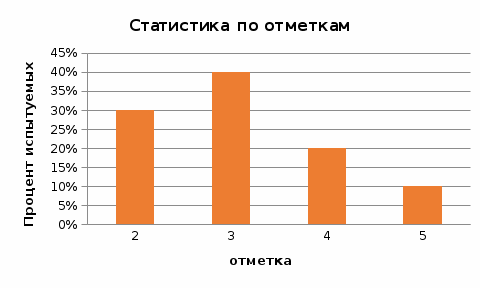 Рис. 17. Статистика по отметкам. Статистические характеристики распределения (на примере ряда индивидуальных тестовых баллов) Для характеристики распределения индивидуальных тестовых баллов (результатов тестирования по группе (класс, школа и т.д.)) используется ряд статистических характеристик – средняя арифметическая, дисперсия, среднеквадратическое отклонение, асимметрия и эксцесс. Также часто используются структурные средние (персентили) распределения. Эти характеристики вариационного ряда могут быть вычислены с помощью функций EXCEL. Средний балл по группе Среднее арифметическое индивидуальных тестовых баллов вычисляется по формуле: 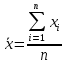 (4) (4)Для вычисления среднего арифметического значения индивидуальных тестовых баллов в EXCEL необходимо выполнить следующие действия. Навести курсор на ячейку, в которую будет записано значение среднего арифметического по группе, нажать ВСТАВКА ФУНКЦИИ, в окне выбрать категорию СТАТИСТИЧЕСКИЕ, в открывшемся окне выбрать СРЗНАЧ и нажать ОК (рис. 18). 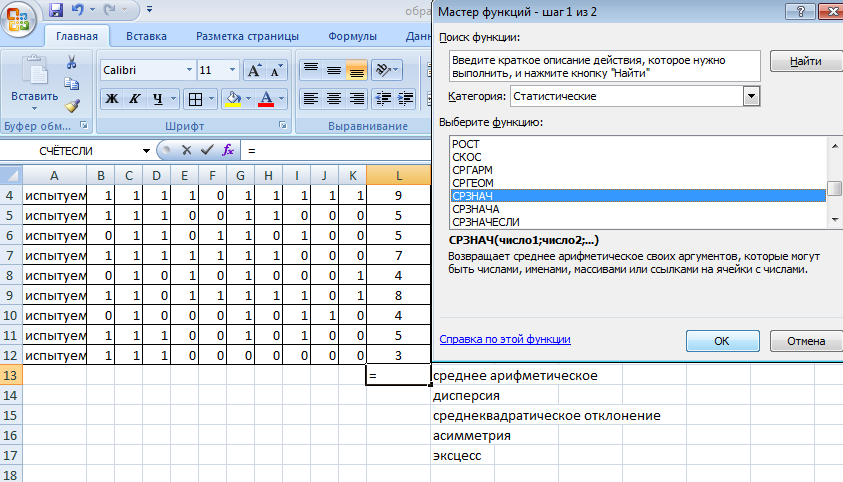 Рис. 18. Вычисление среднего арифметического. В открывшемся окне в первом поле указать диапазон значений, для которого вычисляется среднее арифметическое и нажать ОК (рис. 19). 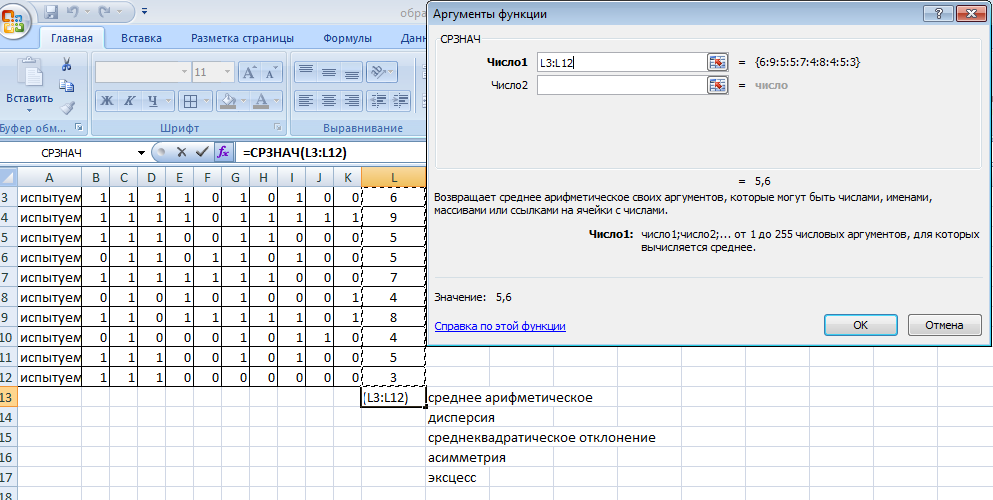 Рис. 19. Вычисление среднего арифметического. Вкладка «Аргументы функции» Вычисленное значение будет записано в указанную ячейку (рис. 20). 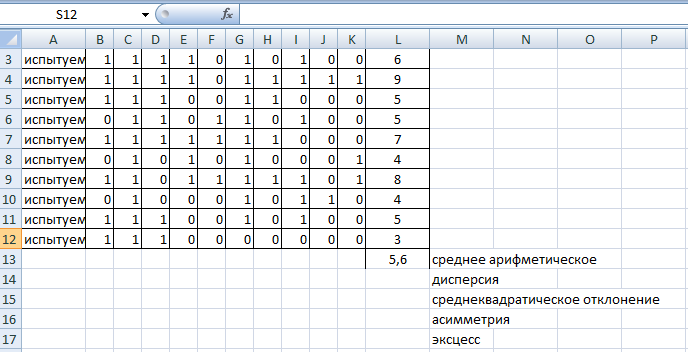 Рис. 20. Вычисление среднего значения Аналогично вычисляются остальные статистические характеристики ряда распределения. Дисперсия вычисляется по формуле: 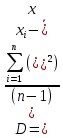 . (5) . (5)Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. Среднеквадратическое отклонение s (в табличном редакторе – стандартное отклонение) вычисляется по формуле: s= 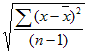 (6) (6)Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений. По величине и знаку асимметрии распределения можно охарактеризовать результат тестирования: какие значения индивидуальных баллов встречаются чаще - высокие (положительная асимметрия) или низкие (отрицательная асимметрия). Для нормального распределения асимметрия равна нулю. Асимметрия вычисляется по формуле: Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Для нормального распределения эксцесс равен нулю. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение. Если распределение остроконечное, то это свидетельствует о достаточно высокой степени однородности группы испытуемых. Их индивидуальные баллы близки. Пологое (сглаженное) распределение характерно для группы испытуемых с большим разбросом индивидуальных тестовых баллов. Эксцесс вычисляется по формуле: 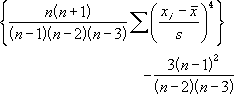 (8) (8) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
