эконометрика. Вариант 6. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице

• Название: Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице
• Анкор: эконометрика
• Дата: 11.11.2022
• Размер: 208.19 Kb.
• Имя файла: Вариант 6.docx
• Тип: Информация; #782328

Ситуационная (практическая) задача №1

Для изготовления продукции двух видов А и В фирма расходует ресурсы, а от реализации этой продукции получает доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице:

Наименование ресурсов	Нормы затрат ресурсов		Объем ресурсов
	А	В
Сырье (кг)	4	1	606
Оборудование (ст.-час.)	1	4	376
Трудовые ресурсы (чел.-час.)	8	1	652
Цена изделия (руб.)	536	191

Задача фирмы заключается в том, чтобы найти план выпуска, обеспечивающий получение максимальной выручки от реализации готовой продукции.

Требуется:

1. 
   Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программирования.
   
2. 
   Используя графический метод решения, найти отптимальный план выпуска продукции.
   
3. 
   Составив двойственную задачу к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения.
   

Решение:

Составим математическую модель задачи.

Введем переменные:

Пусть –объем выпуска изделий вида А;

– объем выпуска изделий вида В.

Используя данные таблицы, определим затраты каждого вида ресурса для выпуска производственной программы :

Расход сырья:

Загрузка оборудования:

Трудовые ресурсы:

Задача состоит в нахождении такой допустимой производственной программы , которая обеспечивает получение наибольшей выручки от реализации:



Построенная математическая модель задачи представляет собой задачу линейного программирования, так как ограничения заданы в виде линейных неравенств, а оптимизируемый показатель (выручка) выражается с помощью линейной функции.

Таким образом, математическая модель данной задачи выглядит следующим образом: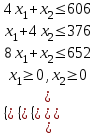



Целевая функция прибыли:

Первым шагом в графическом методе решения является построение множества допустимых решений (МДР), для его построения необходимо построить граничные прямые, уравнения которых получаются из неравенств при замене знака «» на «=».

Граничные прямые можно построить по двум известным точкам:

(1)				(2)					(3)
	110	151,5				0	176				60	81,5
	166	0				94	50				172	0

На рис. 1 показано МДР. МДР представляет собой четырехугольник OABC. Для нахождения точки максимума целевой функции нужно построить градиент функции Z, он равен: . Из начала координат в направлении к точке проводим вектор – по направлению он совпадает с градиентом и показывает направление возрастания функции. Перпендикулярно градиенту проводим некоторую прямую, которая будет являться линией уровня линейной функции Z. Двигая линию уровня параллельной самой себе, можно найти точку максимума, ей будет являться точка Х^* - самая последняя точка МДР, с которой пересечется линия уровня. В нашей задаче точкой максимума является точка В, которая лежит на пересечении линий (2) и (3). Её координаты можно найти, решив систему уравнений:



Тогда максимальный доход от реализации изделий А и В составит:

(руб.)



Рис. 1. Графический метод решения

Оптимальная производственная программа состоит в выпуске 72 изделий вида А и 76 изделий вида В.

Сформируем задачу, двойственную к задаче расчета оптимальной производственной программы и составим обе группы условий «дополняющей нежесткости».

Каждому ресурсному ограничению исходной задачи сопоставляется двойственная переменная (оценка). Так как в нашей задаче рассматриваются три ресурса, то введем для них три оценки, которые обозначим через :



Тогда двойственная задача будет иметь вид:



Найдем предельную эффективность имеющихся у предприятия объемов ресурсов. Допустимые решения прямой и двойственной задачи оптимальны тогда и только тогда, когда выполняются условия «дополняющей нежесткости»:



Для рассматриваемой задачи имеем:



Таким образом, получаем:



В соответствии с вышесказанным найденное оптимальное решение двойственной задачи интерпретируется следующим образом:

руб. - величина ожидаемого роста найденного максимума выручки 53108 руб. от дополнительного вовлечения в производство 1 кг сырья к имеющимся 606 кг. Т.е. ни увеличение, ни уменьшение количества используемого сырья не приведет к изменению величины максимальной выручки.

руб. - величина ожидаемого роста найденного максимума выручки 53108 руб. от дополнительного вовлечения в производство 1 ст.-час. к имеющимся 376 ст.-час.

руб. - величина ожидаемого роста найденного максимума выручки 53108 руб. от дополнительного вовлечения в производство 1 чел.-час. труда к имеющимся 652 чел.-час.

Выполним проверку оптимальных решений прямой и двойственной задачи подстановкой их в ограничения и целевые функции.

Значение целевой функции двойственной задачи составит: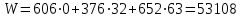

(руб.)

Таким образом, значения целевых функций исходной и двойственной задач совпадают.

В итоге получили следующие результаты расчета модели:



Ситуационная (практическая) задача №2

Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в таблицах:

Имя работы	Опирается на работу	Нормальный срок (дни)	Ускоренный срок (дни)	Нормальная стоимость (млн. руб.)	Срочная стоимость (млн. руб.)
A	E	10	4	13,2	33
B	G, Q	10	4	34,4	86
C		20	8	31,2	78
D	C, F, B	5	2	18,4	46
E	V	10	4	14	35
F	E	5	2	7,6	19
G		13	4	40,4	131,3
H	G, Q	15	6	62,4	156
Q	V	9	2	21,4	96,3
V		5	2	22	55

Требуется:

1. 
   С учетом технологической последовательности работ построить сетевой график выполнения этих работ.
   
2. 
   Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ. Найти критический путь и его продолжительность, указать все возможные критические пути, определить стоимость всего комплекса работ.
   
3. 
   Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 2 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?
   

Решение:

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1, из начального события выпускаются стрелки, соответствующие работам, которым не предшествуют другие работы, в данной задаче начальными работами являются: С, G и V. Все остальные работы в сетевом графике располагаются в зависимости от того, на какие работы они опираются. На рис. 1 приведен сетевой график выполнения работ.



Рис. 1

Рассчитаем временные характеристики сетевого графика:

Раннее время наступления i-го события ( ) – это момент времени, раньше которого событие i не может наступить:



Таким образом, ранее время наступления конечного события сетевого графика составляет 29 дней, т.е. раньше, чем за 29 дней, торговый павильон не может быть построен. Следовательно, критическое время составляет: .

Определим критические пути:

Критическое время было найдено по формуле: 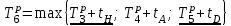, следовательно, работы D и H, на которых достигается максимум, и на которые опирается последнее событие, входит в критический путь.

Работа D, в свою очередь, опираются на работу В, критическое время найдено по формуле: , максимум достигается на работе Q, следовательно, она также входит в критический путь. Работа Н также опирается на работу Q. Работа Q опирается на единственную работу V, следовательно, работа V также входит в критический путь. Таким образом, имеем два критических пути: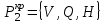





с критическим временем дней.

Временные характеристики и критические пути указаны на рис. 2.



Рис. 2

Стоимость выполнения всего комплекса работ при нормальном режиме их выполнения:

млн. руб.

Необходимо сократить период строительства на 2 дня, т.е. вместо 29 дней построить павильон за 27 дня. Дополнительные затраты  на один день ускорения рассчитываются по формуле: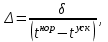



где  - плата за ускорение работы;

- ее длительности при нормальном и ускоренном режиме выполнения;

Результаты расчетов приведены в таблице:

Работа	A	B	C	D	E	F	G	H	Q	V
Максимальное сокращение времени выполнения, дни	6	6	12	3	6	3	9	9	7	3
Удельные затраты на ускорение, тыс. руб./день	3,3	8,6	3,9	9,2	3,5	3,8	10,1	10,4	10,7	11

Сокращение срока строительства будем осуществлять путем ускорения работ, входящих в критические пути. При этом необходимо отслеживать вновь появляющиеся критические пути.

В данном случае наиболее выгодным вариантом будет ускорение работ B и H, входящих в оба критических пути. Ускорим их на 2 дня. В этом случае также остаются два критических пути и 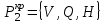с критическим временем дней. Ускоренный график выполнения комплекса работ приведен на рис. 3.



Рис. 3

Стоимость выполнения работ при ускоренном режиме составит:

млн. руб.

Результаты:

Нормальный срок строительства:

Критическое время: дней;

Критические пути: и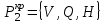

Стоимость выполнения работ: 265 млн. руб.
Ускоренный срок строительства:

Критическое время: дня;

Критические пути: и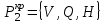

Стоимость выполнения работ: 303 млн. руб.

Тестовые задания

Вопрос	Ответ
	a)
	b)
	c)
	b)
	a)
	c)
	c)
	a)
	c)
	a)