1.Основные понятия ТВ
Опыт- испытание
Событие-результат испытания
Достоверное событие-событие, которое обязательно произойдет при испытании.
Невозможное событие- событие, которое заведомо не произойдет при испытании.
Случайное событие- событие, которое в результате эксперимента может либо произойти, либо не произойти
Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.
Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
Каждое равновозможное событие, которое может произойти в данном опыте называется элементарным исходом.
Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
2.Понятие частоты
Относительной частотой события А, называется отношение числа испытаний, в котором появилось событие А, к общему числу произведенных испытаний.
где mA - число экспериментов, в которых появилось событие А;
n - общее число экспериментов.
|
3. Понятие вероятности события.
Вероятность Р(А) события А равна отношению числа благоприятствующих исходов к общему числу возможных исходов.
С в о й с т в о 1. Вероятность достоверного события равна единице.
Р (A) = m / n = n / n = 1.
С в о й с т в о 2. Вероятность невозможного события равна нулю.
Р (А) = m / n = 0 / n = 0.
С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
0 < Р (А) < 1
Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области W равноправны в отношении попадания точки T. Тогда за вероятность попадания точки T в область A принимается отношение
![[image]](23962_html_2dab188.jpg)
где S(A) и S(W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно.
|
4. Действия над событиями
1. Сумма (объединение) событий (рис. 4.2) представляет собой сложное событие, состоящее в появлении хотя бы одного из событий А и В. Объединение событий обозначается как , или .
2. Произведением (пересечением) событий А и В называется их совместное появление (рис. 4.3). Обозначается произведение событий как , или .
3. Достоверным событием называется событие, которое обязательно происходит в результате данного испытания (рис. 4.4). Оно обозначается обычно как Е.
4. Невозможное событие – событие, которое не может произойти в результате данного испытания. Принятое обозначение – .
5. Несовместными называются события, которые в результате данного испытания не могут произойти вместе (рис. 4.5). Примеры несовместных событий: попадание и промах при выстреле, выпадение двух и трех очков при бросании игральной кости. Рис. 4.5 наглядно показывает, что для несовместных событий .
6. Противоположным к А событием называется событие, состоящее в непоявлении события А (рис. 4.6). Обозначается противоположное событие символом . Примеры противоположных событий: промах и попадание при выстреле, выпадение герба или цифры при одном подбрасывании монеты.
|
5. Элементы комбинаторики
Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
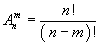
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
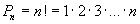
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
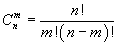
|
6. Правило суммы.
Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B - может быть n способами, то выбрать либо A , либо B можно m+n способами.
Правило произведения. Если некоторый объект A может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект B может быть выбран n способами, то пара объектов (A,B) в указанном порядке может быть выбрана m*n способами.
7.Cумма событий
Суммой событий А и В называется событие А+В состоящее в наступлении хотя бы одного из них.
Теорема: Вероятность суммы несовместных событий А и В равны сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В)
8. Независимые и зависимые события
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А зависит от того, произошло событие В или нет.
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
9. Теорема умножения вероятностей для зависимых и независимых событий
"Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*P(B), т.е. вероятность появления двух независимых событий равна произведению вероятностей этих событий.
"Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*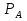 (B) (B)
10. Теория сложения вер-ей для совместн.событий
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
11. Произведение двух и более событий
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
|
12. Формула полной вер-ти и ф.Байеса
Пусть — полная группа событий. Тогда вероятность любого события может быть вычислена по формуле:
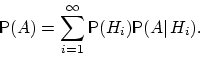
Пусть событие происходит одновременно с одним из несовместных событий 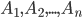 . Требуется найти вероятность события , если известно, что событие произошло. . Требуется найти вероятность события , если известно, что событие произошло.
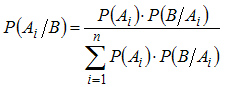
13. Повторные независ. испытания-
многократные испытания, в которых вероятность появления события А в каждом испытании не изменяется в зависимости от исходов других испытаний
Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают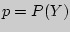 , а непоявления (неудачи) его , а непоявления (неудачи) его 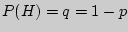 . Бернулли установил, что вероятность ровно успехов в серии из повторных независимых испытаний вычисляется по следующей формуле: . Бернулли установил, что вероятность ровно успехов в серии из повторных независимых испытаний вычисляется по следующей формуле: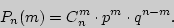
|
14. Локальная теорема Лапласа.
Локальная теорема Муавра-Лапласа.Если вероятность появления события А в каждом из n![[image]](23962_html_m4dfffd60.jpg) независимых испытаний равна одной и той же постоянной р=const (0<р<1), то вероятность независимых испытаний равна одной и той же постоянной р=const (0<р<1), то вероятность ![[image]](23962_html_m5baf8d7b.jpg) того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой: того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой:
![[image]](23962_html_m187ca881.jpg) , где: , где: ![[image]](23962_html_389832fb.jpg) , , ![[image]](23962_html_m10e96da6.jpg) - кривая Гаусса. - кривая Гаусса.
15. Интегральная теорема Муавра-Лапласа.
Пусть вероятность появления события А в каждом из n(n→∞)независимых испытаний равна одной и той же постоянной р (0<р<1), то вероятность ![[image]](23962_html_m5baf8d7b.jpg) того, что во всех этих испытаниях событие А появится не менее k1 и не более k2 раз, приближенно вычисляется формулой: того, что во всех этих испытаниях событие А появится не менее k1 и не более k2 раз, приближенно вычисляется формулой:
![[image]](23962_html_m5a5e954e.jpg) , где , где![[image]](23962_html_4268d765.jpg) - функция Лапласа, - функция Лапласа,
![[image]](23962_html_14fb55ed.jpg) , , ![[image]](23962_html_4faee69d.jpg)
|
16. Теорема Пуассона
При большом числе испытаний постоянной малой вероятности наступления события А в каждом испытании р 0 и при выполнении условия
0,1 ≤np≤10, вероятность того что в n независимых испытаниях событие А наступит ровно m раз, определяется в соответствии с теоремой Пуассона:
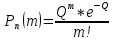 ; ƛ=np ; ƛ=np
n- число испытаний Бернулли
m- число испытаний, в котором наступило событие А
17. Наивероятнейшее число наступления события.
Наивероятнейшее число появления события при независимых испытаниях:
,
- вероятность появления события при одном испытании.
18. Вероятность появления А в n независимых испытаниях хотя бы один раз.
Вероятность появления хотя бы одного из 2 совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
Р(А+В)=Р(А)+Р(В)-Р(АВ)
19. Случайные величины.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
| |
 Скачать 377.97 Kb.
Скачать 377.97 Kb.