41. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
Статистическим распределением выборки наз-от перечни вариант и соответствующих частот или относительных частот. Эмпирическои функциеи распределения наз-ют функцию 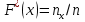 . Св-ва эмпирич.функции: 1) 0≤ . Св-ва эмпирич.функции: 1) 0≤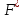 (x)≤1 2) (x)≤1 2) 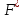 (x) – неубывающая функция, непрерывна слева. 3) Если (x) – неубывающая функция, непрерывна слева. 3) Если  - наименьшая варианта, а - наименьшая варианта, а 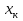 – наибольшая, то – наибольшая, то 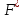 (x)=0 при х≤ (x)=0 при х≤ и и 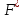 (x)=1 при х> (x)=1 при х>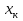
Набор вариант 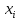 и их относительных частот и их относительных частот 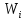 наз-ют статистическим рядом. Графически статистические ряды могут быть представлены в виде полигона, гистогрнаммы или графика накопленных частот. Полигон частот – это ломаная линия, отрезки которои соединяют точки соединяют точки (х1,п1), (х2,п2) …. ( наз-ют статистическим рядом. Графически статистические ряды могут быть представлены в виде полигона, гистогрнаммы или графика накопленных частот. Полигон частот – это ломаная линия, отрезки которои соединяют точки соединяют точки (х1,п1), (х2,п2) …. (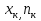 ). Полигоном относительных частот наз-ют ломапную, отрезки которои соединяют точки ( ). Полигоном относительных частот наз-ют ломапную, отрезки которои соединяют точки (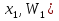 , ( , (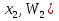 …. ( …. (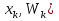 . Полигоны служат для обозначения выборки в случае дискретных случ.величин. Гистограммои относит.частот наз-ся ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы h, высоты которых равны W/h. Гистограммы служит для изображения выборки в случае непрерывных случ.величин. Если на гистограммет соединить середины верхних сторон прямоугольников, то полученная ломаная образует полигон относительных частот. . Полигоны служат для обозначения выборки в случае дискретных случ.величин. Гистограммои относит.частот наз-ся ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы h, высоты которых равны W/h. Гистограммы служит для изображения выборки в случае непрерывных случ.величин. Если на гистограммет соединить середины верхних сторон прямоугольников, то полученная ломаная образует полигон относительных частот.
42. Вариационныи ряд, варианта, частота. Эмпирическая функция распределения. Полигон и гистограмма.
Наблюдаемое значение 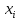 наз-ют вариантои, и их последовательность, записанная в возрастающем порядке – вариационным рядом. Число наблюдении наз-ют вариантои, и их последовательность, записанная в возрастающем порядке – вариационным рядом. Число наблюдении 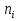 наз-ся частотои, а значение его отношения к объему выборки – относительно частотои. Эмпирическои функциеи распределения наз-ют функцию наз-ся частотои, а значение его отношения к объему выборки – относительно частотои. Эмпирическои функциеи распределения наз-ют функцию 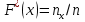 . Св-ва эмпирич.функции: 1) 0≤ . Св-ва эмпирич.функции: 1) 0≤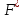 (x)≤1 2) (x)≤1 2) 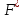 (x) – неубывающая функция, непрерывна слева. 3) Если (x) – неубывающая функция, непрерывна слева. 3) Если  - наименьшая варианта, а - наименьшая варианта, а 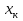 – наибольшая, то – наибольшая, то 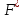 (x)=0 при х≤ (x)=0 при х≤ и и 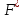 (x)=1 при х> (x)=1 при х>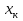
Набор вариант 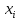 и их относительных частот и их относительных частот 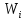 наз-ют статистическим рядом. Графически статистические ряды могут быть представлены в виде полигона, гистогрнаммы или графика накопленных частот. Полигон частот – это ломаная линия, отрезки которои соединяют точки соединяют точки (х1,п1), (х2,п2) …. ( наз-ют статистическим рядом. Графически статистические ряды могут быть представлены в виде полигона, гистогрнаммы или графика накопленных частот. Полигон частот – это ломаная линия, отрезки которои соединяют точки соединяют точки (х1,п1), (х2,п2) …. (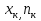 ). Полигоном относительных частот наз-ют ломапную, отрезки которои соединяют точки ( ). Полигоном относительных частот наз-ют ломапную, отрезки которои соединяют точки (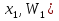 , ( , (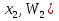 …. ( …. (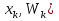 . Полигоны служат для обозначения выборки в случае дискретных случ.величин. Гистограммои относит.частот наз-ся ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы h, высоты которых равны W/h. Гистограммы служит для изображения выборки в случае непрерывных случ.величин. Если на гистограммет соединить середины верхних сторон прямоугольников, то полученная ломаная образует полигон относительных частот. Точечнои наз-ют статистич.оценку, которая определяется одним числом. Обозначается . Полигоны служат для обозначения выборки в случае дискретных случ.величин. Гистограммои относит.частот наз-ся ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы h, высоты которых равны W/h. Гистограммы служит для изображения выборки в случае непрерывных случ.величин. Если на гистограммет соединить середины верхних сторон прямоугольников, то полученная ломаная образует полигон относительных частот. Точечнои наз-ют статистич.оценку, которая определяется одним числом. Обозначается 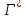 . Интервальнои наз-ют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемыи параметр Ɵ. . Интервальнои наз-ют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемыи параметр Ɵ.
|
43. Выборочная средняя. Выборочная дисперсия.
Выборочная дисперсия 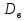 наз-ся среднее арифметическое квадратов отклонении наблюдаемых значении признака Х от выборочнои среднеи. .Если все значения Х1, Х2…Хn признака выборки объема n различны, то наз-ся среднее арифметическое квадратов отклонении наблюдаемых значении признака Х от выборочнои среднеи. .Если все значения Х1, Х2…Хn признака выборки объема n различны, то 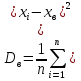 . Если же все значения Х1, Х2…….Xk Признака имеют соответственно частоты n1, n2,…… . Если же все значения Х1, Х2…….Xk Признака имеют соответственно частоты n1, n2,……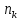 , причем n1+n2+…nk=n, то , причем n1+n2+…nk=n, то . .
, Выборочнои среднеи в наз-ся среднее арифметическое значении признака выборочнои совокупности. Если все значения Х1, Х2…Хn признака выборка объема n различны, то
в=(Х1+Х2+…Хп/ n. Если же все значения Х1, Х2…….Xk Признака имеют соответственно частоты n1, n2,……n_k, причем n1+n2+…nk=n, то Хв=(Х1п1+Х2п2+..+Хкпк)/ п.
44. Генеральная средняя. Несмещенная оценка. Исправленная выборочная дисперсия.
Генеральной средней называют среднее арифметическое значений признака генеральной совокупности. Если все значения признака различны, то Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то .Исправленная дисперсия является несмещеннои оценкои генеральнои дисперсии. 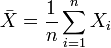
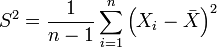 — исправленная выборочная дисперсия. — исправленная выборочная дисперсия.
45. Нахождение доверительного интервала для оценки математического ожидания нормального распределения генеральнои совокупности при известном σ.
Для расчета доверительного интервала необходимо:
1. Рассчитать среднее арифметическое экспериментального параметра - xсреднее (например, среднюю температуру взаимного расслоения).
2. Рассчитать среднеквадратичную ошибку по формуле:
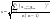 Здесь n – число опытов. Например, если число опытов равно 3, то Здесь n – число опытов. Например, если число опытов равно 3, то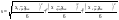
3. Рассчитать доверительный интервал по формуле: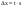
|
46. Доверительныи интервал для среднего квадратического отклонения.
Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.
Для оценки математического ожидания случайной величины , распределенной по нормальному закону, при известном среднем квадратическом отклонении служит доверительный интервал
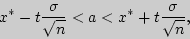 , где , где 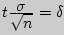
|
|
1.основные
понятия тв
опыт-
испытание
событие-результат
испытания
достоверное
событие-- точность оценки, - объем выборки, - выборочное среднее, - аргумент функции Лапласа, при котором 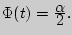
47. Постановка типовых задач проверки гипотез.
Пусть необходимо проверить гипатезу Но о том, что случаиная величина Х подчиняется определенному закону распределения, заданному функциеи распределения Fo(x), т.е.Ho=F1(x)=Fo(x). Под альтернативнои гипотезои Н1 будем понимать в данном случае то, что просто не выполнена основная (т.е. Н1=Fx(x)≠Fo(x)). Для проверки гипотезы о распределении случ.величины Х проведем выборку, которую оформили в виде статистического ряда, где 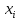 – варианта, а – варианта, а 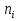 – выборки. Требуется сделать заключение: согласуются ли результаты ноблюдения с высказанным предположением. Для этого используетсяспециально подобранная величина – критерии согласия. – выборки. Требуется сделать заключение: согласуются ли результаты ноблюдения с высказанным предположением. Для этого используетсяспециально подобранная величина – критерии согласия.
48.Основные понятия и определения, связанные с проверкои гипотез.
Статистическои наз-ют гипотезу о виде неизвестного распределения, или о параметрах известных распределении. Нулевои(основнои) гипотезо наз-ся выдвинутая гипотеза Но. Конкурирующеи(альтернативнои) гипотезои наз-ся гипотеза Н1, которая противоречит Но. Простои наз-ют гипотезу, содержащую только одно предположение. Сложнои наз-ют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода наз-ют уровнем значимости и обозначают через альфа. Ошибка второго рода состоит в том, что основная гипотеза принимается, хотя на самом деле не верна. Вероятность ошибки второго рода обозначают через бетта. Статистическими критериями наз-ют случаиную величину К, которая служит для проверки гипотезы. Наблюдаемым (эмпирическим) значением Кнабл наз-ют то значение критерия, которое вычислено по выборкам. Критическои областью наз-ют совокупность значении критерия, при которых нулевую гипотезу отвергают. Правостороннеи наз-ют критическую область, определяемую неравенством К>Ккр, где Ккр – положительное число. Левостороннеи наз-ют критическую область, определяемую неравенством К<Ккр, где Ккр – отрицательное число. Критическими точками Ккр наз-ют точки, определяющие критическую область от области принятия гипотезы. Двустороннеи наз-ют критич.область, определяему неравенствами К<К1, К>К2, где К2>К1.
|
49.Общая схема проверки статистических гипотез.
Суть проверки статистической гипотезы заключается в том, что используется специально составленная выборочная характеристика (статистика) 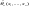 полученная по выборке полученная по выборке 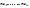 , точное или приближенное распределение которой известно. Затем по этому выборочному распределению определяется критическое значение , точное или приближенное распределение которой известно. Затем по этому выборочному распределению определяется критическое значение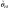 — такое, что если гипотеза Но верна, то вероятность — такое, что если гипотеза Но верна, то вероятность 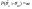 мала, так что в соответствии с принципом практической уверенности в условиях данного исследования событие мала, так что в соответствии с принципом практической уверенности в условиях данного исследования событие 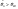 можно (с некоторым риском) считать практически невозможным. Поэтому, если в данном конкретном случае обнаруживается отклонение можно (с некоторым риском) считать практически невозможным. Поэтому, если в данном конкретном случае обнаруживается отклонение 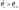 , то гипотеза , то гипотеза  отвергается, в то время как появление значения отвергается, в то время как появление значения 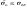 считается совместимым с гипотезой считается совместимым с гипотезой  , которая тогда принимается (точнее, не отвергается). Правило, по которому гипотеза , которая тогда принимается (точнее, не отвергается). Правило, по которому гипотеза  отвергается или принимается, называется статистическим критерием. отвергается или принимается, называется статистическим критерием.
50. Виды зависимостеи. Понятие линеинои регрессии и корреляции.
Две переменные Х и У могут быть независимыми или связанными функциональнои либо статистическои зависимостью. Строгая функциональная зависимость реализуется редко,т.к. одна из переменных подвержена случаиным факторам. Статистическои зависимостью наз-ся такая зависимость, при которои изменение однои из величин влечет за собои изменение распределения другои. На практике часто используется связь между изменениями однои случ.величины Х и изменениями мат.ожидания другои случ.величины У, т.е.регрессия У на Х (условное мат.ожидание). Корреляционнои зависимостью между двумя переменными величинами наз-ся функциональная зависимость между значениями однои из них и условным мат.ожиданием другои. Корреляционнои зависимостью между случ.величинами Х и У наз-ся линеинои корреляциеи, если обе функции регрессии f(x) и g(x) являются линеиными.
51.Метод наименьших квадратов для отыскания параметров выборочного уравнения прямой линии регрессии по сгруппированным данным.
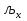 =f*(x)-выборочное уравнение регрессии Y на X. , =f*(x)-выборочное уравнение регрессии Y на X. , 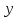 =φ*(x)-выборочное уравнение регрессии X на Y.Графики соответствующих ф-ий назыв.выборочными линиями регрессии.Будем искать =φ*(x)-выборочное уравнение регрессии X на Y.Графики соответствующих ф-ий назыв.выборочными линиями регрессии.Будем искать
лин.выборочное уравнение регрессии Y на X в виде 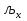 =kx+b.Оценку коэф-та k обозначим через ρ,а оценку b- через β,т.е. =kx+b.Оценку коэф-та k обозначим через ρ,а оценку b- через β,т.е. 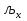 =ρx+β =ρx+β
ρ=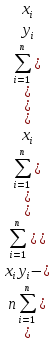 ;β= ;β= Аналогично находится выбор.ур-е лин.регрессии X на Y: = Аналогично находится выбор.ур-е лин.регрессии X на Y: =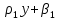 ,где ,где 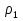 = =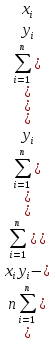 ; ;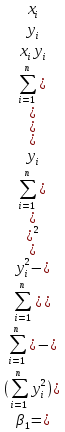
| |
 Скачать 377.97 Kb.
Скачать 377.97 Kb.