27. Непрерывные случайные величины. Функция распределения. Интегральный закон распределения.
Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X
Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
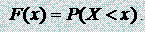
Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям pi для дискретной случайной величины в непрерывном случае. Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения:
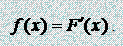
Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью f(x) на определенном участке оси абсцисс. Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид: 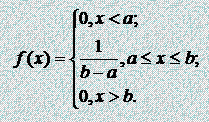
34.Интегральная и дифференциальная ф-ии нормального распределения.Кривая Гаусса.
Интегральной функцией распределения непрерывной случайной величины X называется ф-ия F(x),равная вероятности того,что X приняла значение,меньше x:F(x)=P(X
F(x)-геометрический смысл этого равенства,это вер-ть того,что случ.величина X примет значение,которое изображается на числовой оси точкой,лежащей левее точки x.Функция распределения совершенно так же определяется для дискретных случайных величин.
Плотностью распределения вероятностей непрерывной случ.величины(дифференц.ф-ей распр-я)называют первую производную от ф-ии распределения: F’(x)=f(x)
Ф-ия F(x) общего нормального распределения F(x)=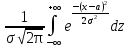 ,а ф-ия нормированного распределения ,а ф-ия нормированного распределения 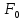 (x)= (x)=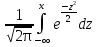 .Ф-ия .Ф-ия 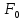 (x) табулирована.Легко проверить,что F(x)=F((x-a)/σ) (x) табулирована.Легко проверить,что F(x)=F((x-a)/σ)
Нормальной кривой Гаусса назыв. график плотности нормального распределения.
35. Понятие и примеры системы случаиных величин.
Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение,наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Более строгое определение случайной величины можно дать следующим образом: Случайной величиной называется функция X(ω), определенная на некотором множестве элементарных событий Ω. Случайные величины обычно обозначают большими буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.Пример 1 Число родившихся мальчиков (или девочек) среди ста новорожденных. Пример2 Число появлений герба при четырех бросаниях монеты. Пример3 Время безотказной работы некоторого прибора.
|
28. Непрерывные случайные величины. Плотность распределения вероятностей непрерывной случайной величины. Дифференциальная функция распределения.
Функцией распределения вероятностей называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее , то есть:
.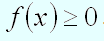
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
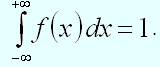
Свойства функции распределения вероятностей случайной величины
Значения функции распределения вероятностей принадлежат отрезку :
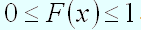
Функция распределения вероятностей – неубывающая функция, то есть:
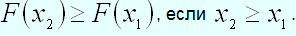
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения вероятностей на этом интервале:
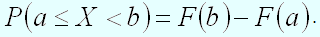
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.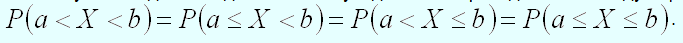
Используя последнее следствие, легко убедиться в справедливости следующих равенств:
Если возможные значения непрерывной случайной величины принадлежат интервалу , то:
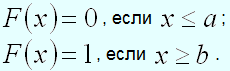
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
;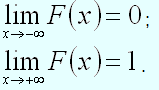
Плотностью распределения вероятностей непрерывной случайной величины называют функцию – первую производную от функции распределения вероятностей :
.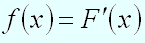
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.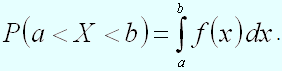
Следовательно, зная плотность распределения вероятности , можно найти функцию распределения по формуле
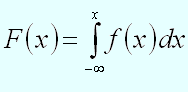
36. Характеристика закона больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим. Приведем данные теоремы и неравенство Чебышева без доказательств.
Неравенство Чебышева (оценка снизу): Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε , не меньше, чем 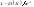 : : 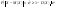 . Неравенство Чебышева (оценка сверху): Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине не меньше положительного числа ε , меньше или равна . Неравенство Чебышева (оценка сверху): Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине не меньше положительного числа ε , меньше или равна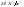 : :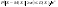 . Теорема Чебышева: Если X1, X2…..Xn,…- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа C) ,то, как бы мало ни было положительное число ε, вероятность неравенства . Теорема Чебышева: Если X1, X2…..Xn,…- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа C) ,то, как бы мало ни было положительное число ε, вероятность неравенства
 будет как угодно близка к единице, если число случайных величин достаточно велико.Другими словами, в условиях теорем будет как угодно близка к единице, если число случайных величин достаточно велико.Другими словами, в условиях теорем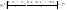 . Теорема Бернулли: Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. . Теорема Бернулли: Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
|
29.Нахождение интегральной функции распределения через дифференциальную ф-ию.Вероятность попадания непрерывной случ.величины в заданный интервал.
Теорема.В-ть попадания непрерывной случ.величины X в интервале(a,b) равна определенному интегралу от ее плотности вер-ти,взятому в пределах от a до b P(-a . В частности,если f(x)-четная ф-ия и концы интервала симметричны относительно начала координат,то P(-a
F(x)=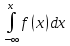 позволяет найти интегральную ф-ию распределения F(x) по ее плотности вероятности. позволяет найти интегральную ф-ию распределения F(x) по ее плотности вероятности.
30. Математическое ожидание непрерывнои случаинои величины.
Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл 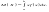
Если возможные значения принадлежат всей оси Ox , то 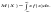 Замечание: Предполагается, что несобственный интеграл сходится абсолютно, то есть существует интеграл Замечание: Предполагается, что несобственный интеграл сходится абсолютно, то есть существует интеграл 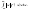
31. Дисперсия непрерывнои случ.величины. Стандартное отклонение.
Дисперсиеи непрерывнои случ.величины наз-ют мат.ожидание квадрата ее отклонения.Если возможные значения Х принадлежат отрезку [а,в], то: M(x)=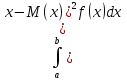 . Если возможные значения принадлежат всеи оси, то: M(x)= . Если возможные значения принадлежат всеи оси, то: M(x)=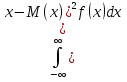 . Так как D(X) = M(X2) – [M(X)]2, то можно использовать следующие формулы для вычисления дисперсии: . Так как D(X) = M(X2) – [M(X)]2, то можно использовать следующие формулы для вычисления дисперсии:
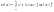 или или 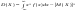 .Замечание: Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины определяется аналогично дискретному случаю: .Замечание: Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины определяется аналогично дискретному случаю: 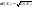 . .
|
32 Нормальное распределение непрерывнои случаинои величины и его параметры. Плотность вероятности нормированного нормального распределения таблица значении этои функции.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается следующей плотностью вероятностей: 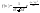 , где , где 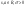 .Стандартным нормальным или нормированным называют нормальное распределение с параметрами .Стандартным нормальным или нормированным называют нормальное распределение с параметрами 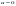 и и 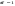 . Например, если X – нормальная величина с параметрами . Например, если X – нормальная величина с параметрами  и и 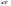 , то , то 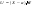 - стандартная нормальная величина, причем - стандартная нормальная величина, причем 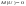 и и 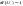 . Плотность стандартного нормального распределения имеет вид . Плотность стандартного нормального распределения имеет вид
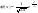 .Функция распределения .Функция распределения  нормального распределения имеет вид: нормального распределения имеет вид: 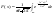 . Функция распределения . Функция распределения 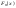 стандартного нормального распределения имеет вид: стандартного нормального распределения имеет вид: 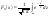 . .
33. Вероятность попадания нормального распределения случ.величины в заданный интервал.Вер-ть заданного отклонения.Правило трех сигм.
В-ть попадания нормально распределенной случайной величины X в интервале(α,β) определяется по формуле:P(αϕ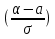
Вероятность отклонения нормально распределенной случ.величины от матем.ожидания по абсолютной величине меньше,чем на δ(δ>0),определяется по формуле:P(│x-a│<σ)=2ϕ(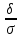 ) (3) ) (3)
Правило трех сигм. Полагая в выражении (3)σ=3σ,получим P(│x-a│<3σ)=2ϕ(3)
39. Математическое ожидание и дисперсия функции одного случ.аргумента для двух случаев: аргумент – непрерывная случ.величина.
Мат.ожиданием непрерывнои случ.величины Х, возможные значения которои принадлежат отрезку [а,в], наз-ют определенныи интеграл.M(x)=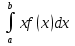 . Если возможные значения принадлежат всеи оси Ох, то: M(x)= . Если возможные значения принадлежат всеи оси Ох, то: M(x)=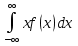 . Дисперсиеи непрерывнои случ.величины наз-ют мат.ожидание квадрата ее отклонения.Если возможные значения Х принадлежат отрезку [а,в], то: M(x)= . Дисперсиеи непрерывнои случ.величины наз-ют мат.ожидание квадрата ее отклонения.Если возможные значения Х принадлежат отрезку [а,в], то: M(x)=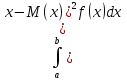 . Если возможные значения принадлежат всеи оси, то: M(x)= . Если возможные значения принадлежат всеи оси, то: M(x)=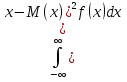 . Среднее квадратическое отклонение равно корню из дисперсии. . Среднее квадратическое отклонение равно корню из дисперсии.
40. Задачи мат.статистики. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативная выборка.
Мат.статистика занимается обработкои результатов случ.эксперимента. ее задачи: 1)Разработка методологии сбора и группировки статистического материала, полученного в результате наблюдении за случ.процессами.2)разработка методов анализа получаемых статистических данных. Этот анализ включает оценку вероятностеи события, функции плотности вероятности, оценку параметров известного распредделения. Генеральнои совокупностью наз-ся множество объектов произвольнои природы, обладающих признаками, доступными для наблюдения и количественного изменения. Распределение Х часто наз-ют распределением генеральнои совокупности. Выборочная совокупность — множество случаев с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании. Если выборки делают по одному объекту, которыи обследуют и снова возвращают в генеральную совокупность, то выборка наз-ся повторнои.Если объекты выборки уже не возвращают, то безповторнои. Репрезентативная выборка - это выборка из генеральной совокупности с распределением F(x), представляющая основные особенности генеральной совокупности.
|
37. Понятие функции одного случайного аргумента. Нахождение распределения функции по известному распределению дискретного и непрерывного аргумента.
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, тоY называют функцией случайного аргу-мента Х: Y = φ(X). Пусть задана функция Y = (X) случайного аргумента X, где аргумент X – дискретная случайная величина с возможными значениями x1, x2,…xn ,вероятности которых соответственно равны p1, p2,…pn. Очевидно, Y - также дискретная случайная величина с возможными значениями (X) случайного аргумента X, где аргумент X – дискретная случайная величина с возможными значениями x1, x2,…xn ,вероятности которых соответственно равны p1, p2,…pn. Очевидно, Y - также дискретная случайная величина с возможными значениями 
А) Если различным возможным значениям аргумента X соответствуют различные возможные значения функции Y, то вероятности соответствующих значений X и Y между собой равны, так как событие “величина X приняла значение xi” влечет за собой событие “величина Y приняла значение  (xi)”, то вероятности возможных значений Y соответственно равны p1, p2,…pn. b) Если различным возможным значениям X соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y. (xi)”, то вероятности возможных значений Y соответственно равны p1, p2,…pn. b) Если различным возможным значениям X соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.
38. Математическое ожидание и дисперсия функции одного случ.аргумента для двух случаев: аргумент – дискретная случ величина.
Пусть некоторая дискретная случ величина Х с конечным числом своих значении задана законом распределения. Мат.ожиданием М(Х) дискретнои случ.величины Х наз-ся сумма произведении всех возможных значении величины Х на соответствующие вероятности. М(Х)=х1р1 + х2р2+…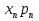 . Теорема: Мат.ожидание дискр.случ.величины Х приближенно равно среднему арифмет.всех ее значении(при достаточно большом числе испытании) Хср=М(Х). Матем.ожидание случ.величины можно приближенно считать ее средним значением, что и делают на практике. Дисперсиеи D(X) дискретнои случ.величины Х наз-ся мат.ожидание квадрата отклонения случ.величины от ее мат.ожидания. D(x)=M[(X – M(X) . Теорема: Мат.ожидание дискр.случ.величины Х приближенно равно среднему арифмет.всех ее значении(при достаточно большом числе испытании) Хср=М(Х). Матем.ожидание случ.величины можно приближенно считать ее средним значением, что и делают на практике. Дисперсиеи D(X) дискретнои случ.величины Х наз-ся мат.ожидание квадрата отклонения случ.величины от ее мат.ожидания. D(x)=M[(X – M(X)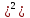 . Из закона распределения величины [X – M(X) . Из закона распределения величины [X – M(X)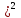 следует, что D(x)=M[(X1 – M(X) следует, что D(x)=M[(X1 – M(X)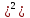 p1 + M[(X2 – M(X) p1 + M[(X2 – M(X)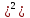 p2 +…. M[(Xn – M(X) p2 +…. M[(Xn – M(X)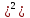 pn. Теорема: Дисперсия равна разности между мат.ожид. квадрата случ.величины Х и квадратом ее мат.ожидания: pn. Теорема: Дисперсия равна разности между мат.ожид. квадрата случ.величины Х и квадратом ее мат.ожидания:
D(X)=M(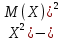
| |
 Скачать 377.97 Kb.
Скачать 377.97 Kb.