52.Выборочный коэффициент корреляции и его свойства.
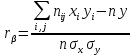 -выборочныи коэффициент корреляции -выборочныи коэффициент корреляции
Св-ва:1).при r±1 коррел. связь представляет лин.функциональную зависимость.При этом линии регрессии Y по X и X по Y совпадают.Значения, наблюдаемые, располагаются на общеи прямои.
2).при r=0 лин.коррел.связь отсутствует
53. Проверка статистических гипотез.
Суть проверки статистической гипотезы заключается в том, что используется специально составленная выборочная характеристика (статистика) 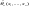 полученная по выборке полученная по выборке  , точное или приближенное распределение которой известно. Затем по этому выборочному распределению определяется критическое значение , точное или приближенное распределение которой известно. Затем по этому выборочному распределению определяется критическое значение — такое, что если гипотеза Но верна, то вероятность — такое, что если гипотеза Но верна, то вероятность 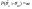 мала, так что в соответствии с принципом практической уверенности в условиях данного исследования событие мала, так что в соответствии с принципом практической уверенности в условиях данного исследования событие 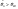 можно (с некоторым риском) считать практически невозможным. Поэтому, если в данном конкретном случае обнаруживается отклонение можно (с некоторым риском) считать практически невозможным. Поэтому, если в данном конкретном случае обнаруживается отклонение 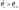 , то гипотеза , то гипотеза  отвергается, в то время как появление значения отвергается, в то время как появление значения 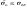 считается совместимым с гипотезой считается совместимым с гипотезой  , которая тогда принимается (точнее, не отвергается). Правило, по которому гипотеза , которая тогда принимается (точнее, не отвергается). Правило, по которому гипотеза  отвергается или принимается, называется статистическим критерием. отвергается или принимается, называется статистическим критерием.
54. Понятие статистическои гипотезы. Нулевая и конкурирующая, простая и сложная гипотезы.
Статистическои наз-ют гипотезу о виде неизвестного распределения, или о параметрах известных распределении. Нулевои(основнои) гипотезо наз-ся выдвинутая гипотеза Но. Конкурирующеи(альтернативнои) гипотезои наз-ся гипотеза Н1, которая противоречит Но. Простои наз-ют гипотезу, содержащую только одно предположение. Сложнои наз-ют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
55. Ошибки первого и второго рода. Критическая область.
Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода наз-ют уровнем значимости и обозначают через альфа. Ошибка второго рода состоит в том, что основная гипотеза принимается, хотя на самом деле не верна. Вероятность ошибки второго рода обозначают через бетта. Обычно ошибка первого рода влечет за собои ошибку второго рода. В целях проверки нулевои гипотезы в рассмотрение вводят специально подобранную случ. величину, распределение которои известно. Критическои областью наз-ют совокупность значении критерия, при которых нулевую гипотезу отвергают.
|
56.Отыскание левостороннеи,правостороннеи и двустроннеи критических областеи.Мощность критерия.
Для отыскания критическо области задаются уровнем значимости и ищут критические точки,исходя из след.соотношении: а)для правост.критич.области P(K>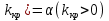 б)для левостор.крит.области P(K< б)для левостор.крит.области P(K<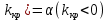 в)для двусторон.симметричнои области P(K> в)для двусторон.симметричнои области P(K>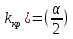 ( (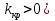 , P(K< , P(K<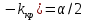 . Мощностью критерия называется вер-ть попадания критерия в критич.область при условии,что справедлива конкурирующая гипотеза.Мощность критерия есть вер-ть того,что нулевая гипотеза будет отвергнута,если верна конкурирующая гипотеза. . Мощностью критерия называется вер-ть попадания критерия в критич.область при условии,что справедлива конкурирующая гипотеза.Мощность критерия есть вер-ть того,что нулевая гипотеза будет отвергнута,если верна конкурирующая гипотеза.
57.Проверка гипотезы о нормальном распределении генеральнои совокупности критерия 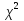 . .
Критерии проверки гипотезы о предполагаемом виде закона распределения случ.величины назыв. критериями согласия.
Для проверки гипотезы 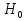 поступают след.образом: Разбивают всю область значении случ.величин X на m интервалов поступают след.образом: Разбивают всю область значении случ.величин X на m интервалов 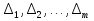 Подсчитывают вер-ти Подсчитывают вер-ти 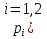 ,…,m)попадания случ.величин X(т.е.наблюдение в интервал ∆;ипользуя формулу P(α≤X≤β)= ,…,m)попадания случ.величин X(т.е.наблюдение в интервал ∆;ипользуя формулу P(α≤X≤β)=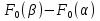 .Тогда теоретич.число значении случ.величин X,попавших в интервал .Тогда теоретич.число значении случ.величин X,попавших в интервал 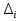 ,можно рассчитать по формуле n ,можно рассчитать по формуле n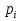
Критерии Пирсона: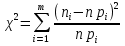 = =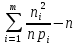 (1) Правило применения критерия (1) Правило применения критерия 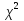 сводится к следующему: 1).По формуле(1) вычисляют сводится к следующему: 1).По формуле(1) вычисляют 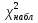 -выбороч.значение статистики критерия.2)Выбрав уровень значимости α критерия,по таблице -выбороч.значение статистики критерия.2)Выбрав уровень значимости α критерия,по таблице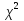 -распределения находим критич.точку (квантиль) -распределения находим критич.точку (квантиль)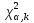 3).Если 3).Если 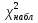 ≤ ≤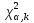 ,то гипотеза ,то гипотеза 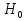 не противоречит опытным данным,если не противоречит опытным данным,если 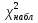 > >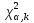 ,то гипотеза ,то гипотеза 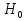 отвергается. отвергается.
|
 Скачать 377.97 Kb.
Скачать 377.97 Kb.