20. Закон распределения дискретной случайной величины
Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного..Закон распределения вероятностей дискретной случайной величины.
21.Математическое ожидание дискретной случайной величины. Свойства
Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу:
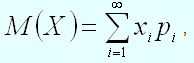
причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства.
Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величин
Свойства математического ожидания

|
22. Дисперсия дискретной случайной величины, ее свойства.
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания D(X) = M(X – M(X))^2. Для вычисления удобнее пользоваться формулой:
D(X) = M(X^2) – (M(X))^2.
Свойства:
1. Дисперсия постоянной величины равна 0: D( C ) = 0,
2. Постоянный множитель можно выносить за знак диперсии, возводя его в квадрат: D (CX) = C^2 D(X),
3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:
D (X+Y+Z) = D(X) + D(Y) + D (Z)
4. Дисперсия суммы постоянной величины и случайной – равна дисперсии случайной величины D(C+X) = D(X).
23. Биномиальное распределение.
Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли:
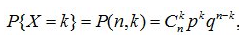
где p – параметр распределения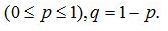
Распределение зависит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение. Числовые характеристики: М [Х] = n, D[X]= npq. Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
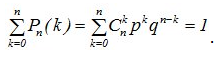
24. Геометрическое распределение.
Дискретная случайная величина X имеет геометрическое распределение, если вероятности ее возможных значений 0,1,….,k,.. определяются так:
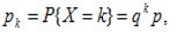
где p – параметр распределения, 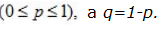
На практике геометрическое распределение появляется при следующих условиях. Пусть производится некоторый опыт, в котором некоторое событие появляется с вероятностью p. Опыты производятся последовательно, до наступления события. Случайная величина X, равная числу неудачных опытов, имеет геометрическое распределение.
Числовые характеристики геометрического распределения:
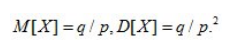
|
25.Равномерное распределение непрерывнои величины. Показательное распределение.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Плотность вероятности равномерного распределения имеет вид:
 Функция распределения вероятностей равномерной случайной величины имеет вид: Функция распределения вероятностей равномерной случайной величины имеет вид: 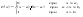
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
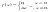 где где  - постоянная положительная величина. функцию распределения показательного закона : - постоянная положительная величина. функцию распределения показательного закона :
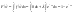 . .
Итак, 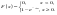
26. Распределение Пуассона.
Одно из важнейших распределений вероятностей случайных величин, принимающих целочисленные значения. Подчинённая П. р. случайная величина Х принимает лишь неотрицательные значения, причём Х = kc вероятностью
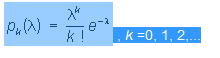 (l — положительный параметр). Своё название "П. р." получило по имени С. Д. Пуассона (1837). Математическое ожидание и дисперсия случайной величины, имеющей П. р. с параметром l, равны l. Если независимые случайные величины X1 и X2 имеют П. р. с параметрами l1 и l2, то их сумма X1 + X2 имеет П. р. с параметрами l1 + l2.В теоретико-вероятностных моделях распределение Пуассона. используется как аппроксимирующее и как точное распределение. Например, если при n независимых испытаниях события A1,..., An осуществляются с одной и той же малой вероятностью р, то вероятность одновременного осуществления каких-либо k событий (из общего числа n) приближённо выражается функцией pk(np) (математическое содержание этого утверждения при больших значениях n и1/р формулируются Пуассона теоремой). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления. (l — положительный параметр). Своё название "П. р." получило по имени С. Д. Пуассона (1837). Математическое ожидание и дисперсия случайной величины, имеющей П. р. с параметром l, равны l. Если независимые случайные величины X1 и X2 имеют П. р. с параметрами l1 и l2, то их сумма X1 + X2 имеет П. р. с параметрами l1 + l2.В теоретико-вероятностных моделях распределение Пуассона. используется как аппроксимирующее и как точное распределение. Например, если при n независимых испытаниях события A1,..., An осуществляются с одной и той же малой вероятностью р, то вероятность одновременного осуществления каких-либо k событий (из общего числа n) приближённо выражается функцией pk(np) (математическое содержание этого утверждения при больших значениях n и1/р формулируются Пуассона теоремой). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления.
|
 Скачать 377.97 Kb.
Скачать 377.97 Kb.