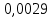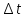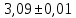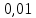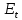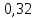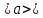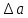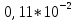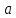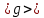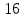Главная страница
Навигация по странице:

  • Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

    		•

    Лабораторная работа №1. Исследование поступательного движения тел на машине Атвуда


    Скачать 161.62 Kb.
    НазваниеИсследование поступательного движения тел на машине Атвуда
    АнкорИсследование поступательного движения тел на машине Атвуда
    Дата22.12.2020
    Размер161.62 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная работа №1.docx
    ТипИсследование
    #163091

    Лабораторная работа №1

    Тема: " Исследование поступательного движения тел на машине Атвуда ".
    Цель работы: Изучение законов поступательного движения системы связанных тел в поле сил тяжести. Определение момента инерции тела относительно оси, проходящей через центр масс тела. 

    Величина
    Единица измерения

    масса
    кг

    время
    с

    высота
    м

    диаметр стержня
    м




    величина
    значение
    Приборная погрешность

    Высота h, м
    0,40
    0,01

    Время, с



    0,001




    m =0.012 кг
    L=0.33 м
    L2=0.23 м

    № наблюдения
    Время ti , с

    1
    0.622

    2
    0.623

    3
    0.625

    4
    0.611

    5
    0.612



    № наблюдения
    ti, с
    ti-, с
    (ti-)2, с2

    1
    0.622
    0,0034
    0,00001156

    2
    0.623
    0,0044
    0,00001496

    3
    0.625
    0,0064
    0,00004096

    4
    0.611
    -0,0076
    0,00005776

    5
    0.612
    -0,0066
    0,00004356

    Суммы
    Σti =3.093
    Σ(ti-)2 =0,00017

     
    Σ =3.093
    Σσ =

     
    Et =1,62%




    0,010

    t


























     Δg







    1.Вычисляем среднее значение времени .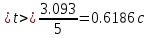

    2. Найдем отклонения каждого из пяти измерений ti от среднего значения времени <t>.

    3. Возведем в квадрат каждое отклонение и просуммируйте квадраты отклонений.

    4.  Рассчитаем среднее квадратичное отклонение σ, применив для его расчёта  формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей.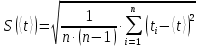



    Буквой 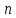  обозначено число измерений, в нашем случае  .



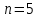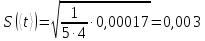    5. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени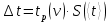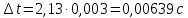





    6.  Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.

    Тогда результат измерения времени t запишем в виде: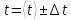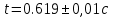




    7. Произвем расчет относительной погрешности в определении времени Et (в процентах) по формуле: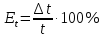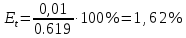





    8. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки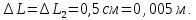



    9. Среднее ускорение грузов <а> рассчитаем по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.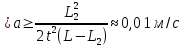



    10. Относительная погрешность в определении ускорения а найдём по формуле: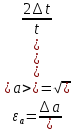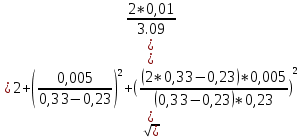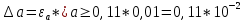







    11. Результат измерения ускорения а запишем в виде: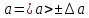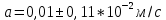





    Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

    12. Определим среднюю величину ускорения свободного падения g по формуле:



    При этом значение массы грузов принять равным M=90 г.

    13. Полуширину доверительного интервала Δg найдем с помощью формулы:



    14. Рассчитайте абсолютную погрешность ускорения свободного падения Δg аналогично погрешности ускорения a. Представьте результат в стандартной форме: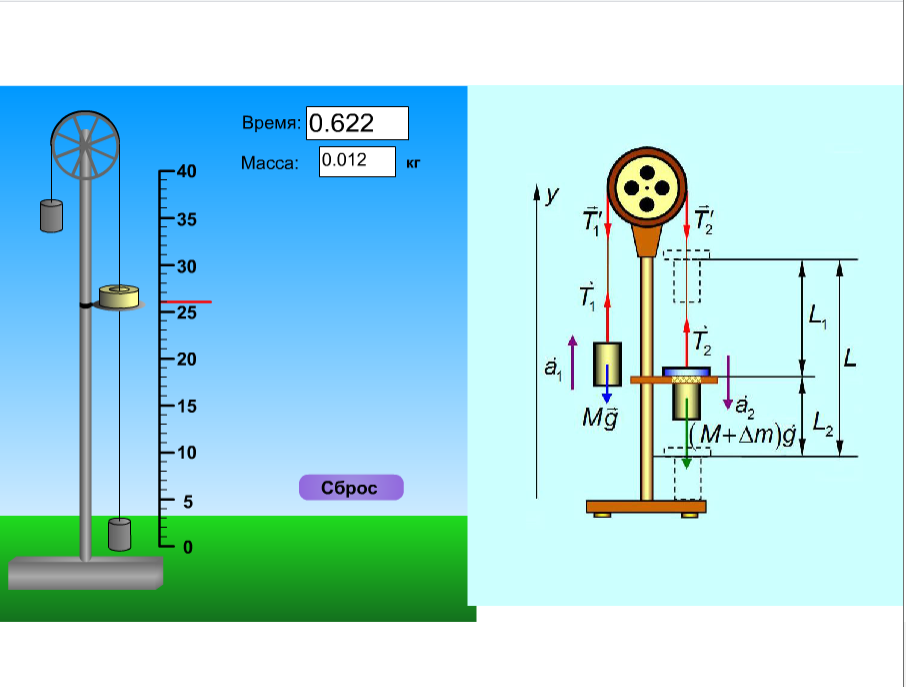

    написать администратору сайта