Белорусский государственный педагогический
университет имени Максима Танка»
Кафедра математики и методики преподавания математики
СОСТАВНОЕ РАСШИРЕНИЕ ПОЛЯ
Курсовая работа
студента 240119 группы
3 курса специальности
«Математика и информатика»
дневной формы
получения образования
____________ Мырадов Кадыр
Допущена к защите
Заведующий кафедрой ________ __________________
(подпись) (фамилия, инициалы)
Протокол № ____ от __________ 2022 г.
Научный руководитель –
профессор, доктор физ-мат. наук
___________ Черняк А.А.
Защищена __________ 2022 г.
с отметкой «_______________»
Минск, 2022
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ………………………………………………………………………..3
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ ПОЛЯ…………………………………….4
Краткий исторический очерк………………………………………4
Понятия поле и конечное поле……………………………………..6
Поле алгебраических чисел………………………………………...7
ГЛАВА 2. РАСШИРЕНИЯ ЧИСЛОВЫХ ПОЛЕЙ……………………………..9
2.1. Простое алгебраическое расширение поля………………………9
2.2. Составное алгебраическое расширение поля……………………14
ЗАКЛЮЧЕНИЕ………………………………………………………………….21
СПИСОК ЛИТЕРАТУРЫ……………………………………………………….22
ВВЕДЕНИЕ.
В педагогических вузах введена программа единого курса алгебры и теории чисел. Главная цель этого курса—изучение основных алгебраических систем и воспитание алгебраической культуры, необходимой будущему учителю для глубокого понимания целей и задач как основного школьного курса математики, так и школьных факультативных курсов.
На наш взгляд, наиболее целесообразным является введение в школьное преподавание элементов современной абстрактной алгебры.
Начавшийся в ХХ веке процесс алгебраизации математики не прекращается, а это вызывает упорные попытки введения в школьное математическое образование основных алгебраических понятий.
Математическая глубина и необычайно широкая сфера применения полей сочетаются с простотой ее основных положений – понятий полей, целый ряд важных теорем можно сформулировать и доказать, обладая начальными представлениями в области теории множеств. Поэтому теория полей как нельзя лучше подходит для того, чтобы показать школьникам образец современной математики.
Кроме того, изучение элементов теории поля полезно для школьников, способствует их интеллектуальному росту, проявляющемуся в развитии и обогащении различных сторон их мышления, качеств и черт личности, а также воспитанию у учащихся интереса к математике, к науке.
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ ПОЛЯ
Краткий исторический очерк
Алгебра прошла несколько этапов в своем развитии. Сейчас решению линейных и квадратных уравнений обучают в средней школе, поэтому кажется, что решать их совсем просто. Но пока не появились буквенные обозначения, знаменитые a, b и c все квадратные уравнения записывались словами. Представим, что квадратное уравнение записано так: возьми известное количество, два раза умноженное на неизвестное количество, добавляем к этому второе известное количество, умноженное на неизвестное количество, добавляем к этому третье известное количество, в сумме получаем ничего. Вот такая задачка, и необходимо найти это неизвестное количество. Древние египтяне с этой задачей справились именно в такой формулировке. Правда, учили этому много лет, но когда человек обучался, он находил ответ точно в таком же виде, как формулируется задача. Потом на протяжении очень долгого времени делались попытки решить уравнения третьей и четвертой степени. В конце концов решения были получены, и люди научились решать и эти уравнения. Далее возникла задача решения уравнения 5-й степени. И вот здесь начались сложности. Долгие безуспешные попытки найти формулу для решения уравнения 5-й степени закончились тем, что Абель доказал невозможность решения этой задачи в радикалах. Потом появляется Галуа. Он погиб в возрасте 20 лет, но зато оставил после себя работу, которая предопределила развитие алгебры на много лет вперед. Созданные Галуа теории продолжают использоваться в современной математике. Галуа предложил рассуждение, которое до сих пор является одним из основных средств рассуждений в алгебре. Представим, что надо решить некоторую задачу. Задача сложная и решается с трудом. Можно идти двумя путями: можно сесть и решать, а можно пойти по другому пути. Например, пока не придумали мнимые числа, некоторые квадратные уравнения было нельзя решить, а вот когда ввели эту мнимую единичку, все сразу стало просто. Значит, второй способ состоит в том, чтобы расширить множество (чисел) так, чтобы у задачи появилось решение. Галуа предложил очень общий метод решения уравнений. Если они не решаются, надо расширить множество возможных решений, точно также, как и в случае уравнения второй степени. И он предложил такие расширения, которые позволяют решать уравнения любой степени. Это так называемые расширения Галуа. Эта идея до настоящего времени является одной из основных в современной математике.
Огромное значение в развитии теории чисел имели замечательные работы К. Гаусса (1777-1855). Гаусс наряду с изучением обычных чисел начал рассматривать так же и арифметику чисел, получивших название целых гауссовских чисел, а именно числа вида a+bi, где a и b – обычные целые числа. Эти его исследования положили начала алгебраической теории чисел.
Теория алгебраических чисел была построена в работах Куммера (1810-1893) и Дирихле (1805-1859) и развита затем Кронекером (1823-1891), Дедекиндом (1831-1916) и Е.И. Золотаревым (1847-1878). Работы Лиувилля (1809-1882) и Эрмита (1822-1901) явились основой трансцендентных чисел.
Вопросы аппроксимации алгебраических чисел рациональными были существенно продвинуты в начале века А. Туэ, а затем в пятидесятых годах в работах К. Рота.
В последнее время все большее внимание специалистов по теории чисел привлекает алгебраическая теория чисел.
Здесь надо назвать работы Г. Хассе, Е. Гекке, а в особенности французского математика А. Вейля, результаты которого были использованы во многих теорико-числовых исследованиях, как например Д. Берджессом в проблеме о наименьшем квадратичном вычете.
К алгебраической теории чисел относятся и интересные работы советского математика И.Р. Шафаревича, а так же работы Б.Н. Делонга по теории кубических форм.
Понятия поле и конечное поле
Поле - множество, для элементов которого определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), причём свойства этих операций близки к свойствам обычных числовых операций. Простейшим полем является поле рациональных чисел (дробей). Хотя названия операций поля взяты из арифметики, следует иметь в виду, что элементы поля не обязательно являются числами, и определения операций могут быть далеки от арифметических. Для полей характерны следующие свойства: Характеристика поля всегда 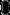 или простое число.: Количество элементов в конечном поле всегда равно или простое число.: Количество элементов в конечном поле всегда равно  - степени простого числа.: В поле нет делителей нуля. - степени простого числа.: В поле нет делителей нуля.
Конечное поле
Конечное поле или поле Галуа - поле, состоящее из конечного числа элементов.
Конечное поле обычно обозначается 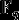 или или 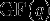 (сокращение от Galois field), где (сокращение от Galois field), где  - число элементов поля (мощность). С точностью до изоморфизма конечное поле полностью определяется его мощностью, которая всегда является степенью какого-либо простого числа ( - число элементов поля (мощность). С точностью до изоморфизма конечное поле полностью определяется его мощностью, которая всегда является степенью какого-либо простого числа (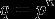 , где , где 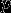 - простое число, являющееся характеристикой поля). - простое число, являющееся характеристикой поля).
Понятие конечного поля используется, в частности, в теории чисел, алгебраической геометрии, теории Галуа, криптографии, в разработке секретных ключей различных шифров (например, AES).
Простейшим примером конечного поля является 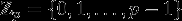 - кольцо вычетов по модулю простого числа - кольцо вычетов по модулю простого числа 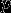 . .
Свойства конечного поля:
R1: Характеристика конечного поля является простым числом, и число элементов конечного поля есть его характеристика в натуральной степени:

R2: Конечное поле не может быть упорядоченным, так как упорядоченное поле содержит бесконечно много элементов.
R3: Мультипликативная группа  конечного поля конечного поля 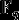 является циклической группой порядка является циклической группой порядка 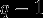 . .
R4: Поле  содержит в себе в качестве подполя содержит в себе в качестве подполя 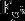 тогда и только тогда, когда тогда и только тогда, когда 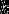 является делителем является делителем  . .
Поле алгебраических чисел.
В классе подполей поля комплексных чисел одним из наиболее важных является поле алгебраических чисел.
Определение. Алгебраическим числом называется комплексное число, являющееся корнем полинома положительной степени с рациональными коэффициентами.
Отметим, что алгебраическое число есть любое комплексное число, алгебраическое над полем Q. В частности, любое рациональное число является алгебраическим.
Теорема. Множество A всех алгебраических чисел замкнуто в кольце E = С, +, —, •, 1 комплексных чисел. Алгебра A = А, +, —, •, 1 является полем, подполем поля E.
Доказательство. Пусть a и b — любые элементы из А. По следствию 2.6, поле Q(a, b) является алгебраическим над Q. Поэтому числа a+b, -а, ab, 1 являются алгебраическими, т. е. принадлежат множеству A. Таким образом, множество А замкнуто относительно главных операций кольца E. Поэтому алгебра A — подкольцо кольца E — является кольцом.
Кроме того, если a —ненулевой элемент из А, то a-1 Q (a, b) и поэтому а-1 принадлежит А. Следовательно, алгебра A есть поле, подполе поля E.
Определение. Поле A = А, +, —, •, 1 называется полем алгебраических чисел.
Пример.
Показать, что число =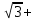  является алгебраическим. является алгебраическим. Решение. Из =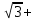  следует - следует -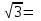  . . Возведем обе части последнего равенства в третью степень: 3-32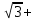 9-3 9-3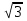 =2 =2
или
3 +9-2=3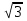 (a2+1). (a2+1).
Теперь обе части равенства возводим во вторую степень:
a6+18a4+81a2-4a3-36a+4=27a4+54a2+27
или
a6-9a4-4a3+27a2-36a-23=0.
Таким образом a является корнем многочлена
f(x)= a6-9a4-4a3+27a2-36a-23=0
с рациональными коэффициентами. Это значит что a — алгебраическое число.
ГЛАВА 2. РАСШИРЕНИЯ ЧИСЛОВЫХ ПОЛЕЙ.
2.1. Простое алгебраическое расширение поля.
Простое расширение поля.
Пусть P[x] — кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент поля F называется алгебраическим над полем P, если является корнем какого-нибудь полинома положительной степени из P [x].
Определение. Пусть P < F и F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозначается через P (a), основное множество поля P (a) обозначается через Р(a).
Пусть aF, P [x] — кольцо полиномов от x и
P[x]={f(a)fP[x]},
т. е. P [a] есть множество всех выражений вида a0 + a1a+...+ anan, где а0, a1,...anP и n — любое натуральное число.
Легко видеть, что алгебра P[a], +, —, ., 1 — подкольцо поля P (a) — является кольцом; это кольцо обозначается символом P [a].
Теорема. Пусть P [x]— кольцо полиномов от х над P и P (a)— простое расширение поля P. Пусть — отображение P[x] на P[] такое, что (f)=f() для любого f из P[x]. Тогда:
(а) для любого а из Р (а) = а;
(b) (x) = ;
(с) является гомоморфизмом кольца P [x] на кольцо P [a];
(d) Ker ={fP[x]f()=0};
(е) фактор-кольцо P [x]/Кег изоморфно кольцу P [].
Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения . Отображение сохраняет главные операции кольца P [x], так как для любых f и g из P[x]
(f + g)=f()+g(), (fg)= f()g(), (1)=1.
Далее, по условию, есть отображение Р[х] на Р[]. Следовательно, является гомоморфизмом кольца P [x] на кольцо P [].
Утверждение (d) непосредственно следует из определения отображения .
Поскольку — гомоморфизм кольца P [x] на P [], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a].
Следствие. Пусть a — трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a].
Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0} P [a]. Кроме того, фактор-кольцо кольца P [x] по нулевому идеалу изоморфно P [x]. Следовательно, P [x] P [a].
Минимальный полином алгебраического элемента.
Пусть P [x] — кольцо полиномов над полем P.
Определение. Пусть a — алгебраический элемент над полем P. Минимальным полиномом элемента a, над P называется нормированный полином из P[x] наименьшей степени, корнем которого является a. Степень минимального полинома называется степенью элемента a над P.
Легко видеть, что для всякого элемента a, алгебраического над P , существует минимальный полином.
Предложение. Если а — алгебраический элемент над полем P, а g и — его минимальные полиномы над P, то g=.
Доказательство. Степени минимальных полиномов g и совпадают. Если g , то элемент a (степени n над P) будет корнем полинома g - , степень которого меньше степени полинома (меньше n), что невозможно. Следовательно, g=.
Теорема. Пусть a — алгебраический элемент степени n над полем P (aP) и g — его минимальный полином над P. Тогда:
(а) полином g неприводим в кольце P [x];
(b) если f (a) = 0, где f P[x], то g делит f;
(с) фактор-кольцо P [x]/(g) изоморфно кольцу P [a];
(d) P [x]/(g) является полем;
(е) кольцо P [a] совпадает с полем P (a).
Доказательство. Допустим, что полином g приводим в кольце P [x], т. е. существуют в P[x] такие полиномы и h, что
g = h, 1deg , deg h
Тогда g(a) = (a)h(a) = 0. Так как P (a) — поле, то ( a) = О или h(a) = 0, что невозможно, поскольку, по условию, степень элемента a над P равна п.
Предположим, что f P[x] и f(a) = 0. По условию, g(a) = 0. Следовательно, f и g не могут быть взаимно простыми. Поскольку полином g неприводим, то g делит f.
Пусть — гомоморфизм кольца P [x] на кольцо P [a] ((f)=f(a) для всякого f из P[x]), рассмотренный в теореме. В силу (Ь) ядро гомоморфизма состоит из кратных полинома g, т.е. Кег = (g). Следовательно, фактор-кольцо P = P [x]/(g) изоморфно кольцу P [a].
Поскольку P[a]P(a), то P [a] есть область целостности. Так как P P[a], то фактор-кольцо P также есть область целостности. Нам надо показать, что любой ненулевой элемент f из P обратим в P. Пусть f — элемент смежного класса f. Так как f 0, то f(a)0; поэтому полином g не делит полином f. Поскольку полином g неприводим, отсюда следует, что полиномы f и g — взаимно простые. Следовательно, в Р[x] существуют такие полиномы u и v, что uf + vg=1. Отсюда вытекает равенство uf = 1, показывающее, что элемент f обратим в кольце P. Итак, установлено, что фактор-кольцо P является полем.
В силу (с) и (d) P [a] является полем и поэтому P(a)P[a]. Кроме того, очевидно, P[a]P(a). Значит, P[a] = P(a). Следовательно, кольцо P [a] совпадает с полем P (a).
Строение простого алгебраического расширения поля.
Теорема. Пусть a — алгебраический над полем P элемент положительной степени n. Тогда любой элемент поля P(a) однозначно представим в виде линейной комбинации n элементов 1, a, ..., an-1 с коэффициентами из Р.
Доказательство. Пусть — любой элемент поля P (a). По теореме, P(a) = P[a]; следовательно, существует в P[x] полином f такой, что
(1) = f(a).
Пусть g — минимальный полином для a над P; в силу условия теоремы его степень равна п. По теореме о делении с остатком, существуют в P[x] полиномы h и r такие, что
(2) f = gh + r, где r = 0 или der r < der g = n , т. е. r=c0+c1x +…cn-1xn-1 (ciP). Полагая в (2) x = а и учитывая равенство (1), имеем
(3) = c0+c1a +…cn-1an-1
Покажем, что элемент однозначно представим в виде линейной комбинации элементов 1, a, ..., an-1. Пусть
(4) = d0+d1a +…dn-1an-1 (di P)
—любое такое представление. Рассмотрим полином
= (с0 – d0) + (c1 - di.)x + . . . + (сn-1 –dn-1)xn-1
Случай, когда степень меньше n, невозможен, так как в силу (3) и (4) (a) = 0 и степень меньше степени g. Возможен лишь случай, когда = 0, т. е. с0 = d0, . . . , сn-1 = dп-1. Следовательно, элемент однозначно представим в виде линейной комбинации элементов 1, a,…,an-1.
Освобождение от алгебраической иррациональности в знаменателе дроби.
Задача об освобождении от алгебраической иррациональности в знаменателе дроби состоит в следующем. Пусть a — алгебраический элемент степени n>1 над полем P; f и h — полиномы из кольца полиномов P [x]и h(a) 0. Требуется представить элемент f(a)/h(a)0P(a) в виде линейной комбинации степеней элемента a, т. е. в виде (a),
где 0P[x].
Эта задача решается следующим образом. Пусть g — минимальный полином для a над P. Так как, по теореме, полином неприводим над P и h(a) 0, то g не делит h и, значит, полиномы h и g — взаимно простые. Поэтому существуют в P[x] такие полиномы u и v, что
uh+vg=1 (1)
Поскольку g(a) = 0, из (1) следует, что
u(a)g(a) = 1, 1/h(a) = u(a).
Следовательно, f(a)/h(a) = f(a)u(a), причем f,u 0P[x] и f(a)u(a)0P[a]. Итак, мы освободились от иррациональности в знаменателе дроби f(a)/h(a) .
Пример.
Освободиться от иррациональности в знаменателе дроби
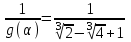 . .
Решение. В нашем случае = . Минимальным многочленом этого числа является . Минимальным многочленом этого числа является
p(x)=x3-2.
Многочлены p(x) и g(x)=-x2+x+1 взаимно просты. Поэтому существуют такие многочлены и , что
p+g=1.
Для отыскания и применим алгоритм Евклида к многочленам p и g:
  -x3-2 -x2+x+1 -x2+x+1 2x-1 -x3-2 -x2+x+1 -x2+x+1 2x-1
 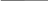     x3-x2-x -x-1 -x2+1/2x -1/2x+1/4 x3-x2-x -x-1 -x2+1/2x -1/2x+1/4
  x2+x-2 1/2x+1 x2+x-2 1/2x+1
x2-x-1 1/2x-1/4
  2x-1 5/4 2x-1 5/4
Таким образом,
p=g(-x-1)+(2x-1),
g=(2x-1)(-1/2x+1/4)+5/4.
Откуда находим
(2x-1)=p+g(x+1),
5/4=g-(p+g(x+1))(-1/2x+1/4)
или
p1/5(2x-1)+g(4/5+1/5(2x2+x-1))=1,
p1/5(2x-1)+g(2/5x2+1/5x+3/5)=1.
Таким образом,
(x)= (2/5x2+1/5x+3/5).
Тогда
y()=y( )= )=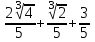 . .
Следовательно
 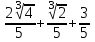 . .
2.2. Составное алгебраическое расширение поля.
Конечное расширение поля.
Пусть P — подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, т. е. рассматривать векторное пространство F, +, { 0P},
где - операция умножения элементов из F на скаляр 0P.
Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F : P].
Предложение. Если a — алгебраический элемент степени n над P, то [P (a):P]=n.
Это предложение непосредственно следует из теоремы.
Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебраическим над P.
Теорема. Любое конечное расширение F поля P является алгебраическим над P.
Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, a, ..., an, т. е. существуют в P такие элементы с0, с1,…,cn не все равные нулю, что с01+ с1a+…+cn an = 0.
Следовательно, элемент a является алгебраическим над P.
Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.
Повторное алгебраическое расширение поля
Будем рассматривать только алгебраические расширения полей
Пусть поля P, F, G таковы, что  причем причем  - простое алгебраическое расширение поля P, а - простое алгебраическое расширение поля P, а 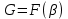 - простое алгебраическое расширение поля F. Тогда поле G является повторным алгебраическим расширением поля P и обозначается - простое алгебраическое расширение поля F. Тогда поле G является повторным алгебраическим расширением поля P и обозначается 
Теорема. Пусть дано повторное алгебраическое расширение 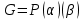 поля P и степень алгебраического над полем P элемента поля P и степень алгебраического над полем P элемента 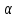 равна k, а степень алгебраического над полем равна k, а степень алгебраического над полем  элемента элемента 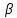 равна m. Тогда равна m. Тогда 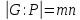 и система векторов и система векторов  является базисом расширения G поля P. является базисом расширения G поля P.
Составное алгебраическое расширение поля.
Расширение F поля P называется составным, если существует
возрастающая цепочка подполей L i поля F такая, что
P = L0 L1 … Lk= F и k>1.
Теорема. Пусть F — конечное расширение поля L и L — конечное расширение поля P. Тогда F является конечным расширением поля P и
[F : P] = [F : L][ L : P].
Доказательство. Пусть
(1) a1,…,am — базис поля L над P (как векторного пространства) и
(2) 1,…,n — базис поля F над L . Любой элемент d из F можно линейно выразить через базис:
(3) d = l11+...+lnn (lk 0L).
Коэффициенты 1k можно линейно выразить через базис (1):
(4) lk = p1k a +…+ pmk am (pik0P).
Подставляя выражения для коэффициентов lk в (3), получаем
d = pik aik.
i0{1,…,m}
k0{1,…,n}
Таким образом, каждый элемент поля F представим в виде линейной комбинации элементов множества B, где
B = { a ik{1,..., m}, k 0 {l,..., n}}.
Отметим, что множество B состоит из nm элементов.
Покажем, что B есть базис F над полем P. Нам надо показать, что система элементов множества B линейно независима. Пусть
(5) cikaik = 0,
I,k
где cik 0 P. Так как система (2) линейно независима над L , то из (5) следуют равенства
(6) с1ka 1+...+сmka m = 0 (k = 1,..., n).
Поскольку элементы a 1, ..., a m линейно независимы над P, то из (6) следуют равенства
c1k = 0,…,cmk = 0 (k = 1, ..., n),
показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов B линейно независима и является базисом F над P.
Итак установлено, что [F , P] = nm = [F: L][L: P]. Следовательно, F является конечным расширением поля P и имеет место формула (I).
Определение. Расширение F поля P называется составным алгебраическим, если существует возрастающая цепочка подполей поля P
P = L0 — L1 —…— Lk= F и k>1 (1)
такая, что при i = 1,..., k поле L i является простым алгебраическим расширением поля L i-1. Число k называется длиной цепочки (1).
Следствие. Составное алгебраическое расширение F поля P является конечным расширением поля P.
Доказательство легко проводится индукцией по длине цепочки (1) на основании теоремы.
Теорема. Пусть 1,..., k — алгебраические над полем P элементы поля F . Тогда поле P(1,..., k) является конечным расширением поля P.
Доказательство. Пусть
L 0 = P, L 1 = P [1], L 2= P [1, 2,],..., L k = P [1 ,..., k].
Тогда L1 = P [1] есть простое алгебраическое расширение поля L0; L2 есть простое алгебраическое расширение поля L1 , так как
L2 = P [1,2] = (P [1])[2] = L1[a2] = L1(a2) и т. д.
Таким образом,
P = L0 — L1 —…— Lk= F
где Li = Li-1(ai ) при i = 1, ..., k, т. е. каждый член цепочки (2) является простым алгебраическим расширением предшествующего члена цепочки. Итак, поле F является составным алгебраическим расширением поля P. Следовательно, в силу следствия поле F является конечным расширением поля P .
Следствие. Составное алгебраическое расширение поля является алгебраическим расширением этого поля.
Простота составного алгебраического расширения поля.
Теорема. Пусть числовое поле F есть составное алгебраическое расширение поля P . Тогда F является простым алгебраическим расширением поля P.
Доказательство. Пусть P —L — F , причем L = P(), F = L() и, следовательно, F = P(, ).
Пусть f и g — минимальные полиномы над P соответственно для чисел и и deg f = m, deg g = n. Полиномы f и g неприводимы над P и, следовательно, не имеют в поле E комплексных чисел кратных корней. Пусть
= 1 ,..., m — корни полинома f в C и
= 1 ,..., n — корни полинома g в C.
Рассмотрим конечное множество М:
M = {(i-)/(-k)i{1,…,m}, k{2,…,n}}.
Поскольку P — числовое множество (и, значит, бесконечное), то в P существует число c, отличное от элементов множества М, cPМ, cМ. Пусть
(1) = + c.
Тогда выполняются соотношения
(2) i +ck = (i{1,..., m}, k{2, ..., n}).
В самом деле, в случае равенства +с = i+сk было бы
с = (i-)/(-k) M
что противоречило бы выбору числа c.
Пусть F1 = P () и F1 — кольцо полиномов от x. Пусть h = f( - cx) — полином из F1[x] (, cP() = F1). Покажем, что x- есть наибольший общий делитель полиномов h и g в кольце F1[x]. Так как g() = 0, то x- делит g в E[x]. Далее, в силу (1)
h() = f(-c) = f() = 0.
Поэтому x- делит полином h в E[x]. Таким образом, x- есть общий делитель h и g в кольце E[x].
Докажем, что g и h в С не имеет корней, отличных от . В самом деле, допустим, что k, k{2 ,..., n}, есть их общий корень. Тогда h(k) = f( - сk) = 0. Следовательно, найдется такой индекс i{1 ,..., m}, что = ai+cbk (k>1), а это противоречит (2). На основании этого заключаем, что x- есть наибольший общий делитель g и h в E[x]. Поскольку x - — нормированный полином, то отсюда следует, что x - является наибольшим общим делителем g и h в кольце F1[x]. Поэтому
(x-) F1[x] и F1 = P().
Кроме того, = - c F1. Таким образом,
F = P(, ) F1, F1F.
Следовательно, F = P(). Далее, так как (как и всякий элемент из F) есть алгебраический элемент над P и F = P (), то поле F = P () является искомым простым алгебраическим расширением поля P.
Алгебраическая замкнутость поля алгебраических чисел.
Теорема. Поле алгебраических чисел алгебраически замкнуто.
Доказательство. Пусть A [x] — кольцо полиномов от x над полем A алгебраических чисел. Пусть
f = а0 + а1x+... + аnхn (а0 ,…, аn A)
— любой полином положительной степени из A[x]. Нам надо доказать, что f имеет корень в А. Так как fC[x] и поле E алгебраически замкнуто, то f имеет корень в E т. е. существует такое комплексное число с, что f(с) = 0. Пусть L= Q(а0, ..., аn) и L (с) — простое алгебраическое расширение поля L с помощью с. Тогда Q —L — L (c) есть конечное алгебраическое расширение поля L. По теореме , L есть конечное расширение поля Q. В силу теоремы L (с) является конечным расширением поля Q. Отсюда, по теореме 2.2, следует, что поле L (с) является алгебраическим расширением поля Q и, значит, cA. Таким образом, любой полином из A[x] положительной степени имеет в A корень, т. е. поле A алгебраически замкнуто.
ЗАКЛЮЧЕНИЕ.
В данной курсовой работе рассмотрены основные алгебраические расширения полей, во-первых, ввиду той фундаментальной роли, которую поля играют в современной математике, во-вторых, ввиду относительной простоты этого понятия.
В курсовой работе были рассмотрены следующие виды расширений числового поля P:
Простое алгебраическое расширение поля.
Составное алгебраическое расширение поля.
Анализируя работу можно сделать некоторые выводы.
Из рассмотренных в первых двух частях расширений, таких как:
простые алгебраические расширения;
конечные расширения;
составные алгебраические расширения.
Следует, что все эти виды расширений совпадают и, в частности, исчерпываются простыми алгебраическими расширениями поля P.
СПИСОК ЛИТЕРАТУРЫ
1. С. В. Ларин. Алгебра и теория чисел. – Москва, Юрайт, 2021 (стр. 123-128)
2. Л.Я. Куликов. Алгебра и теория чисел.— М.: Высш. Школа,1979.—528-538с.
3. Б.Л. Ван-дер-Варден. Алгебра.— М.,1976 — 138-151с.,158-167с.,244-253с.
4. Э.Ф. Шмигирев, С.В. Игнатович. Теория многочленов.— Мозырь 2002.
|
 Скачать 105.79 Kb.
Скачать 105.79 Kb.
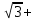
 является алгебраическим.
является алгебраическим.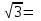
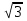 =2
=2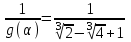 .
.

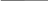


 x3-x2-x -x-1 -x2+1/2x -1/2x+1/4
x3-x2-x -x-1 -x2+1/2x -1/2x+1/4
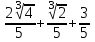 .
.
 - простое алгебраическое расширение поля P, а
- простое алгебраическое расширение поля P, а 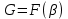 - простое алгебраическое расширение поля F. Тогда поле G является повторным алгебраическим расширением поля P и обозначается
- простое алгебраическое расширение поля F. Тогда поле G является повторным алгебраическим расширением поля P и обозначается 
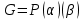 поля P и степень алгебраического над полем P элемента
поля P и степень алгебраического над полем P элемента 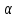 равна k, а степень алгебраического над полем
равна k, а степень алгебраического над полем 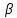 равна m. Тогда
равна m. Тогда 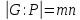 и система векторов
и система векторов  является базисом расширения G поля P.
является базисом расширения G поля P.