рабочая программа. Конспект урока по теме Определение степени с целым отрицательным показателем
 Скачать 121 Kb. Скачать 121 Kb.
|
|
Муниципальное бюджетное общеобразовательное учреждение основная общеобразовательная школа с. Колдаис Конспект урока по теме: «Определение степени с целым отрицательным показателем». Учитель математики: Живаева Любовь Николаевна 2013 год Тип урока.Урок изучения и первичного закрепления новых знаний, который является первым в системе уроков по теме "Степень с целым показателем". Цель урока.Организоватьдеятельность учащихся по формированию понятия степени с целым отрицательным показателем, научить применять его при вычислениях и преобразованиях выражений, содержащих степени. Задачи: Обучающие. 1. Повторить определение и основные свойства степени с натуральным показателем, ввести определение степени с целым отрицательным показателем, 2. Формировать умения: - преобразовывать выражение в дробь или произведение, используя определение степени с целым отрицательным показателем; - вычислять степени с отрицательным показателем; - представлять числа в виде степени с целым показателем, - упрощать выражения, содержащие степень с целым показателем. Развивающие. 1. Продолжить развитие умений выделять главное, существенное в изучаемом материале, обобщать, делать выводы, выбирать рациональный способ решения. Продолжить развитие логического мышления, математической речи. Развивать познавательный интерес к предмету, кругозор учащихся. Воспитательные. 1. Воспитание воли, стремления к получению новых знаний, умения доводить начатое до конца, преодолевать трудности. Формировать самооценку знаний, творческую активность, аккуратность, дисциплину, внимание. 2. Учить работать в группах и парах, формировать умение выслушивать мнения и доводы товарищей, отстаивать свою точку зрения. Оборудование:мультимедийный проектор, презентация, плакат, карточки с заданиями. ХОД УРОКА1. Организация начала урока.Приветствие учащихся, проверка готовности учащихся к уроку (открыли тетради, записали число, классная работа); концентрация внимания на восприятие учебного материала. Постановка целей урока (слайды 1,2). 2. Повторение ранее изученного материала. 1. Определение степени с натуральным показателем (слайд 3). 2. Определение степени числа с показателем 1(слайд 4). 3. Определение степени числа, не равного нулю, с нулевым показателем (слайд 4). 4. Свойства степени с натуральным показателем (слайд 5). 5. Задания устного характера (слайд 6): 3,54; (-0,1)3 –прочитать выражение, назвать основание, показать степени; (-а)6; (-х)13 – каким числом по знаку будет результат вычисления, почему? х5х8; а21:а; (m4)7; (6/у)2 - представьте в виде степени; (-0,9)2; 810; (-1/4)1; (1/3)8; 10-4 – возведите в степень. 4. Изучение нового материала. Проблемная ситуация: возведите в степень - 10-4. Как вы думаете, это положительное или отрицательное число? (слайд 7) Ответы учащихся. Чтобы выяснить какой ответ правильный, выполним задание. В тетради с последующей проверкой (слайд 8,9,10): Задание. 1) Уловите закономерность и продолжите ряд чисел вправо и влево ...,10, 100, 1000, ... ...1/10000, 1/1000,1/100,1/10, 1, 10, 100, 1000, 10000... 2) Представьте каждое из чисел в виде степени с основанием 10: ...,1/104,1/103,1/102, 1/101, 10°, 101, 102, 103,104,... 3) Начиная с 100, подпишите под числами показатели степеней: ...1/104 ,1/103,1/102, 1/101, 10°, 101, 102, 103,104,... -4 -3 -2 -1 0 1 2 3 4 Сравните показатели соседних степеней.( Показатель каждой степени на 1 меньше следующего). Распространите эту закономерность на числа слева от 10°. Получается такая строка: …,10-4,10-3,10-2,10-1,100,101,102,103,104,… Из последней записи видим 10-4 =1/104 =1/10000 = 0,0004 Мы убедились в том, что степень с отрицательным показателем число положительное. Итак 10-1=1/10, 10-2=1/102, 10-3=1/103 . Такое соглашение принимается для степеней с любым основанием, отличным от нуля. Вопрос учащимся. Почему 0 не может быть основание с отрицательным показателем степени? Вывод. 0n имеет смысл только при положительных значениях n. Откройте учебники на с. 204, прочитайте определение. Запишите в тетради формулу: an = l/a-n, a≠0. 0n –не имеет смысла при целом отрицательном n. Первичное закрепление знаний (с последующей проверкой). Работа с таблицами. Замените степень с целым отрицательным показателем дробью:
Замените дробь степенью с отрицательным показателем:
Вычислите:
II. Сравните результат вычисления, как называются пары чисел: 125 и 1/125; 729 и 1/729; 512 и 1/512. Вывод: аn и а-n взаимно обратные числа аn ∙ a-n =an ∙ 1/an = 1 и а-1 = 1/aФизкультминутка для глаз «Космос».III.В тетради - представьте в виде степени с положительным основанием: (2/3)-4 = 1/(2/3)4 =1/24/34 = 1: 24/34 = 1∙34/24 = 34/24 =(3/2)4Вывод: для возведения дроби в целую отрицательную степень удобнее использовать формулу (а/b)-n = (b/а)n.I |
| 10-6 | 9-2 | а-1 | х-20 | (ав)-3 | (а+в)-4 | Количество правильных ответов |
| | | | | | | |
2. Замените дробь степенью с отрицательным показателем:
| 1/102 | 1/67 | 1/х | 1/у10 | 1/7 | 1/(а+в)5 | Количество правильных ответов |
| | | | | | | |
3.Вычислите:
| 53 | 5-3 | 36 | 3-6 | 29 | 2-9 | Количество правильных ответов |
| | | | | | | |

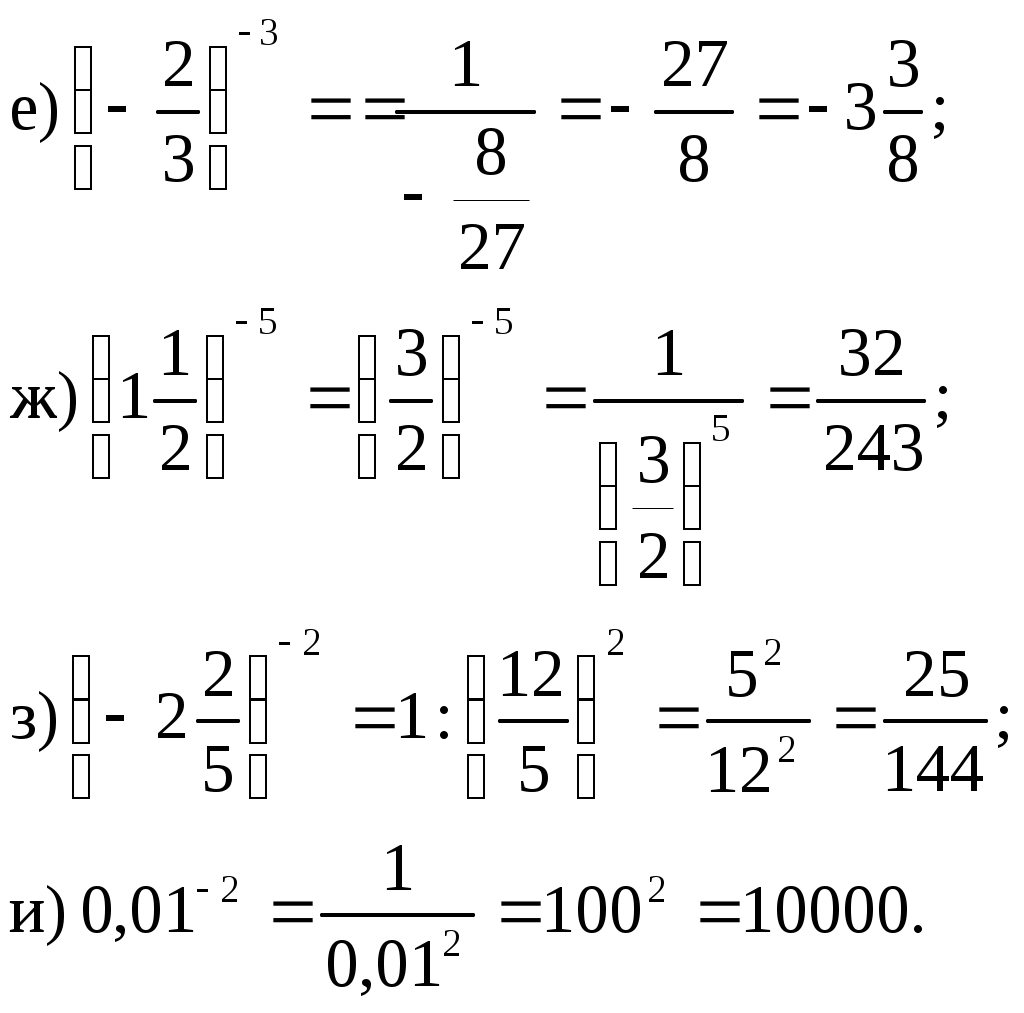 V
V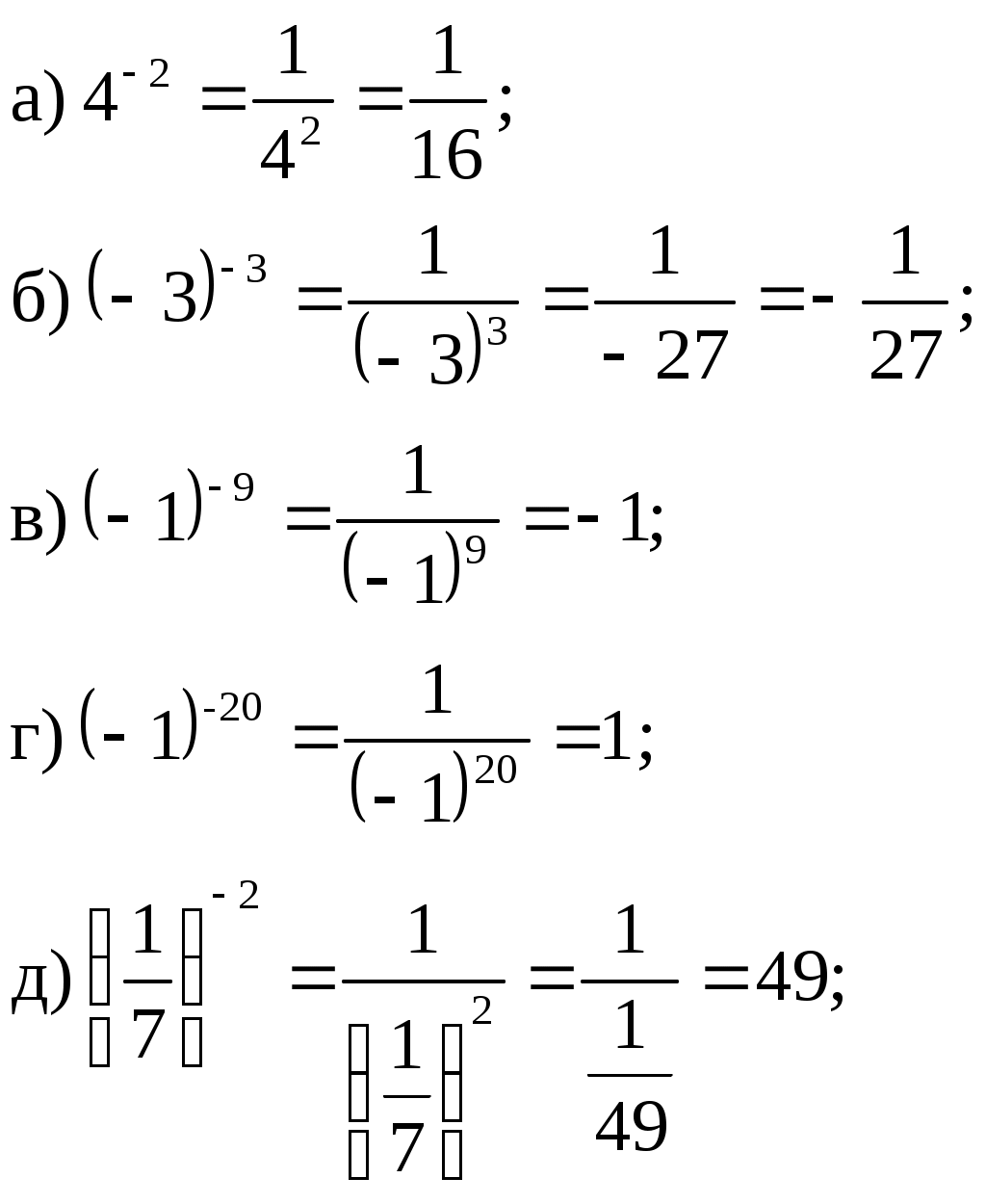 Вычислите:
Вычислите:  своей знаменитой «Арифметике» греческий учёный Диофант описывает первые натуральные степени чисел так: «Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от
своей знаменитой «Арифметике» греческий учёный Диофант описывает первые натуральные степени чисел так: «Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от