фыв. Документ Microsoft Word. Контрольная работа дисциплина Теория систем и системный анализ Тема Управление сложными системами общие положения и разбор примеров
 Скачать 37.24 Kb. Скачать 37.24 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» КОНТРОЛЬНАЯ РАБОТА
Екатеринбург 2023 СодержаниеВВЕДЕНИЕВопрос о возможностях эффективного управления той или иной системой всегда считался достаточно важным вне зависимости от того, к какой сфере деятельности таковая система принадлежит. Особенно актуальным этот вопрос является в отношении социально-экономических и политических систем, при этом достаточно ясно, что различные типы систем требуют, вообще говоря, различных способов управления, которые, в свою очередь, должны опираться на адекватные методы анализа и прогнозирования возможного поведения объектов управления. В области социально-экономических и политических наук такими методами, по существу, единственными, являются методы математического моделирования. И хотя построение и исследование математических моделей зачастую требует привлечения достаточно громоздкого аппарата, современный уровень развития данной области науки позволяет во многих случаях вести изложение на содержательном уровне и делать общие качественные выводы, которые, если не забывать о всегда существующих границах применимости соответствующих моделей, могут быть полезными для реального применения. Объект – Общее положение Предмет - особенности управление сложными системами, общее положение, а так же разбор примеров. Вначале, исключительно для упрощения, попробуем пояснить некоторые понятия. Состояние любой системы можно оценить по набору значений параметров, которые могут быть как фиксированными, так и функциями (например, от времени), для краткости все эти параметры объединим в векторе 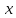 . При этом допустим, что параметры, определяющие структуру системы, также могут входить в состав . При этом допустим, что параметры, определяющие структуру системы, также могут входить в состав 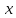 , обозначим их , обозначим их 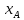 , а остальные (координаты) обозначим , а остальные (координаты) обозначим 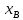 . Кроме того, если система управляемая, то существует другой набор параметров (управлений) . Кроме того, если система управляемая, то существует другой набор параметров (управлений) 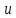 , которые можно менять, изменяя таким образом состояние системы. В итоге каждой паре состояний-управлений , которые можно менять, изменяя таким образом состояние системы. В итоге каждой паре состояний-управлений 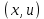 будет соответствовать еще один набор параметрову-реакция системы, которая в принципе может содержать и состояния будет соответствовать еще один набор параметрову-реакция системы, которая в принципе может содержать и состояния 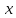 , но необязательно с ними совпадает. Подчеркнем, что в набор , но необязательно с ними совпадает. Подчеркнем, что в набор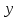 здесь включены только те параметры, значения которых могут меняться при различных значениях управлений и состояний. Поэтому, если набор здесь включены только те параметры, значения которых могут меняться при различных значениях управлений и состояний. Поэтому, если набор 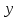 не содержит параметров не содержит параметров 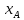 , то это значит, что сама система не меняется по отношению к управлению и ее можно в таком случае назвать простой или технической. Если же реакция , то это значит, что сама система не меняется по отношению к управлению и ее можно в таком случае назвать простой или технической. Если же реакция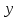 содержит параметры содержит параметры 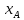 , то для различных значений управления структура системы будет различной, т.е. внешние воздействия приводят к изменению самой системы и ее можно назвать сложной. Разумеется, существует множество других определений этих понятий и классификаций типов систем, но здесь определения даны лишь для использования по ходу дальнейшего текста работы. , то для различных значений управления структура системы будет различной, т.е. внешние воздействия приводят к изменению самой системы и ее можно назвать сложной. Разумеется, существует множество других определений этих понятий и классификаций типов систем, но здесь определения даны лишь для использования по ходу дальнейшего текста работы.Для управления простыми системами, очевидно, можно применить оптимизационный подход, т.е. выделить из набора один или несколько параметров, по которым оценивается качество управления и затем решить одно- или многокритериальную задачу оптимизации по выбору из допустимого множества управлений оптимального набора управляемой системы, доставляющего желаемое наибольшее или наименьшее значение критериям качества. Конечно, решение этой задачи может вызвать и большие трудности, но они могут быть в той или иной степени удовлетворительно разрешены уже в рамках теории оптимизации. Гораздо большие и принципиально иные трудности возникают при управлении сложными системами, в смысле принятого определения. В то же время именно такие системы и являются основными объектами изучения в социально-экономических и политических науках. Типичной и очень распространенной ошибкой моделирования и анализа сложных систем является попытка их аппроксимации простыми системами и использованием таких же, т.е. оптимизационных, моделей. Приведем простой пример. Пусть имеется фирма, выпускающая два товара, по запасам ресурсов на рассматриваемый период общий объем не должен превосходить двух единиц, при этом цены на товары зависят от объемов их выпусков следующим образом: 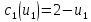 и и 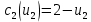 , т.е. увеличение объема приводит к снижению цены. , т.е. увеличение объема приводит к снижению цены. Фирма естественно стремится к максимальной стоимости проданных товаров. Таким образом, исходную систему можно считать сложной, поскольку цены (параметры структуры системы) зависят от выпусков (управлений). Обычно квалификация систем как сложной происходит из-за наличия в ее составе активных элементов (подсистем), обладающих своими собственными интересами и определенными возможностями выбора своих действий, который зависит от состояний-управлений и приводит к изменению структуры самой системы. Для управления сложными детерминированными системами можно применять равновесный подход, где выбор понятия равновесия зависит от типа получившейся математической модели. Этот тип равновесия будет определять и адекватный математический аппарат исследования, современный уровень развития которого примерно такой же, что и у теории оптимизации, т.е. в принципе позволяет ответить на вопросы о существовании равновесия, единственности решения, а также о способах его вычисления. Прежде всего, по аналогии с механикой, равновесное состояние системы обычно понимают как точку взаимного погашения всех имеющихся в системе воздействий, т.е. как в механике, равнодействующая всех приложенных к этой точке сил равна нулю. Это означает, что равновесное состояние может длиться сколь угодно долго, а соответствующей математической моделью равновесия будет система уравнений (линейных или нелинейных). Очевидно, что такой подход вряд ли приемлем для общих сложных систем. Предлагается в качестве основы для обобщения понятия равновесия использовать само свойство существования системы как целого на протяжении определенного временного периода. В этом случае равновесие может быть как статическим, так динамическим, т.е. меняться по времени и представлять целую траекторию (последовательность) состояний по времени. Кроме того, равновесие может быть не обязательно полным, когда оно относится ко всем параметрам системы, но частичным, т.е. когда наблюдаются стабильные связи между некоторыми параметрами. Даже в этом случае равновесная математическая модель может дать содержательные результаты об исходной системе. Например, модель межотраслевого баланса В.В. Леонтьева основана на свойстве неизменности только коэффициентов межотраслевых затрат 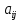 - объема продукции -й отрасли, используемого для производства единицы продукции - объема продукции -й отрасли, используемого для производства единицы продукции 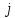 -й отрасли за финансированный период времени, все остальные параметры системы, описывающей обычно экономику целой страны или группы стран, могут принимать в принципе произвольные значения. коэффициенты -й отрасли за финансированный период времени, все остальные параметры системы, описывающей обычно экономику целой страны или группы стран, могут принимать в принципе произвольные значения. коэффициенты 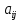 тогда вычисляются по статистическим данным за предыдущие периоды. Используя уравнения баланса (сохранения), теперь можно оценить объемы выпуска тогда вычисляются по статистическим данным за предыдущие периоды. Используя уравнения баланса (сохранения), теперь можно оценить объемы выпуска 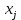 для каждой -й отрасли, которые обеспечивают заданный уровень непроизводственных затрат для каждой -й отрасли, которые обеспечивают заданный уровень непроизводственных затрат 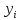 продукции этой отрасли: продукции этой отрасли: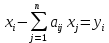 , , 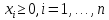 ; ;Eсли экономика разделена на 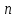 отраслей. Условия неотрицательности добавлены по смыслу переменных отраслей. Условия неотрицательности добавлены по смыслу переменных 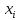 . Полученная система линейных уравнений и неравенство допускает весьма эффективные способы анализа и успешно применяется к реальным задачам, если при этом не забывать об условиях, обеспечивающих неизменность коэффициентов межотраслевых затрат. Более того, эта модель может быть применена и к описанию динамических процессов. . Полученная система линейных уравнений и неравенство допускает весьма эффективные способы анализа и успешно применяется к реальным задачам, если при этом не забывать об условиях, обеспечивающих неизменность коэффициентов межотраслевых затрат. Более того, эта модель может быть применена и к описанию динамических процессов. Важнейшей особенностью устойчивого равновесия является то, что в этом состоянии нет необходимости в явном контроле всех взаимосвязей и параметров системы, т.е. имеет место свойство саморегулирования которое делает возможным эффективное управление общими сложными системами на основе изменения значений сравнительно небольшого числа управляющих параметров. Сказанное требует более подробного и предметного пояснения, которое снова сделаем на примере моделей экономического равновесия. Очевидно, что это свойство саморегулирования системы или ее частей в состоянии равновесия делает в принципе возможным управление общими сложными системами в любой области. В то же время эволюция методов управления сложными системами проходила по принципу проб и ошибок, вызывающих порой изменение карты мира, но при этом вместе с прямыми методами управления обычно присутствовали и косвенные. Необходимость введения ограничений в экономических системах также осознавалась довольно давно, например, можно вспомнить закон Владимира Мономаха об ограничении суммы процентов, возвращаемой по займу. Правительство Екатерины II вместе с усилением административного контроля принимало меры по свободе торговли и ремесел для стабилизации обстановки в стране. Эффективность методов косвенного воздействия (управления) осознавалось не сразу, поскольку прямые методы были яснее и проще и для понимания, и для реализации, причем в самых различных областях деятельности. Например, в господствовавший в театральном искусстве классицизм с его фиксированными принципами и прямым морализаторством стали проникать черты непрямого воздействия, пока не оформились окончательно в новой концепции драматургии А.П. Чехова, где основное воздействие происходит за счет психологического подтекста пьесы. Разумеется, сказанное не означает, что равновесный подход является единственным или наилучшим среди других подходов. На самом деле, чем больше различных подходов к построению модели исследованной реальной системы, тем лучше, поскольку такие модели будут взаимно дополнять друг друга и представлять исследователю нетривиальные сведения о реальной системе. Главное здесь – понимание всех существующих возможностей для построения адекватной модели. В городе планируется построить кинотеатр. Есть проекты на 250, 400, 500 и 600 посадочных мест. Стоимость обслуживания кинотеатра составляет 1000 рублей в день и дополнительно 400 рублей за каждые 100 посадочных мест (более 400). Вы можете проводить 6 сеансов в день. Средняя стоимость билета составляет 100 рублей. Количество посетителей, по оценкам экспертов, варьируется от 1000 до 4000 человек в день. Какой из кинопроектов мне следует выбрать? Учитывая возможный поток зрителей от 1000 до 4000 с "шагом" в 500 человек, сформулируйте задачу как игру с природой, постройте матрицу прибыли для игрока А (LPR, владелец кинотеатра) и решите задачу – предложить оптимальный выбор стратегии LPR) используя критерии Байеса, Лаплас, Вальд, Сэвидж, Гурвиц, Ходж-Леман. Для критерия Байеса-Лапласа примем вероятности возможного числа зрителей равными {0,1; 0,15; 0,2; 0,2; 0,15; 1,15; 0,05}. Что можно сказать о применимости критерия Эрмейера к данной ситуации? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
