Экономика. Контрольная работа по дисциплине статистика вариант 7 Обучающийся 12100 Исхакова А. Ф
 Скачать 75.02 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ» (КНИТУ-КАИ) Высшая школа технологий и менеджмента КОНТРОЛЬНАЯ РАБОТА по дисциплине: СТАТИСТИКА вариант 7 Обучающийся _____12100____ ____________ Исхакова А.Ф. (номер группы) (подпись, дата) (Ф.И.О.) Руководитель старший преподаватель Нефедова Ю.В. (должность) (Ф.И.О.) Контрольная работа зачтена ______________________ (подпись, дата) Казань 2020 THE MINISTRY OF SCIENCE AND HIGHER EDUCATION OF THE RUSSIAN FEDERATION Federal State Budgetary Educational Institution of Higher Education «Kazan National Research Technical University named after A.N.Tupolev-KAI» (KNRTU-KAI) Institute of Engineering Economics and Entrepreneurship (Name of Institute (Faculty), Branch) Department of Industrial Economics and Management (Name of Department) 38.03.01 «Economics» (Code and Name of Academic Major (Speciality)) COURSE WORK on the subject: STATISTICS option 7 Student ___12100____ ____________ A.F. Iskhakova (group number) (signature, date) (Initials, Surname) Supervisor senior lecturer Y.V. Nefedova (title) (Initials, Surname) Course Work has been credited with the mark ________________ ___________________ (signature, date) Kazan 2020 ОГЛАВЛЕНИЕ Задача 1.1………………..…………………….……………….…..…….….4 Задача 1.10…………………………………...………………………...…..10 Задача 1.15…………………..………………….……………….……....…11 Задача 1.16…………………..………………….……………….……...….15 Задача 1.23…………………..………………….……………….……...….18 Заключение……………………………………………………………….. Список использованной литературы……………..……………...………20 Задача 1.1. По данным 50 предприятий о среднесписочной численности рабочих (таблица 1) произвести группировку и вычертить гистограмму, определить среднюю арифметическую, моду и медиану, показатели вариации. Таблица 1 – Основные технико-экономические показатели 50 заводов
Решение: Ранжируем заводы по среднесписочной численности персонала и определим ее минимальное и максимальное значения:  Оптимальное число интервалов определим по формуле Стерджесса: 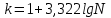  – объем совокупности Определим ширину интервала по формуле:  Границы интервалов будут следующие (табл.2): Таблица 2 Границы интервалов группировки
Интервальный ряд распределения заводов по среднесписочной численности ППП представлен в табл. 3. Таблица 3 Распределение заводов по среднесписочной численности ППП
Построим гистограмму распределения.  Рис. 1 – гистограмма распределения заводов по среднесписочной численности ППП Таблица 4 Данные для расчета показателей распределения
Среднюю величину среднесписочной численности ППП уровень определим по формуле средней арифметической взвешенной:  Мода – это значение признака, наиболее часто повторяющееся в совокупности. Мода в интервальном ряду рассчитывается по формуле:  где  – нижняя граница модального интервала;  - частоты соответственно, модального интервала, интервала, предшествующего модальному, и интервала, последующего за модальным.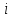 – ширина модального интервалаВ данном распределении наибольшая частота 17 соответствует интервалу (391 – 452), следовательно, он является модальным.  Медиана – это значение признака, делящее ряд распределения на две равные части. Медиана (Ме) в интервальном ряду определяется по формуле:  где  – нижняя граница медианного интервала;  – накопленная частота интервала, предшествующего медианному;  - собственная частота медианного интервалаМедианным является первый интервал, имеющий накопленную частоту, превышающую половину объема выборки (>50/2=25). В заданном распределении – это интервал (391 – 452) с накопленной частотой 28.  Рассчитаем дисперсию:  Среднее квадратическое отклонение равно:  Рассчитаем коэффициент вариации:  Среднее число работников по совокупности заводов составило 460 чел. со среднеквадратическим отклонением – 103 чел. Дисперсия равна 10557,51. Так как коэффициент вариации меньше 22,3%, то распределение однородно и рассчитанное среднее типично для всей совокупности. Мода характеризует наиболее вероятное число работников, равное 413 чел. Медиана показывает, что среднесписочная численность персонала половины заводов составляет не менее 441 чел., а другой половины – не более 441 чел. Задача 1.10 Каковавероятность того, что предельная ошибка выборочной средней стоимости покупок на 1 покупателя не превысит 1,6 р., а предельная ошибка частности покупателей, приобретших товаров на сумму более 60 р. не превысит 0,04 при опросе 10% из общего количества 4000 покупателей магазина. Среднее квадратическое отклонение равно 16 р. Из общего числа опрошенных покупателей 80 купили товаров больше, чем на 60 р. Решение: Рассчитаем среднюю ошибку бесповторной выборк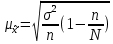и:   – объем выборки – объем генеральной совокупности – по условию – дисперсия признака (квадрат среднеквадратического отклонения) Предельная ошибка уточняет среднюю на коэффициент доверия: 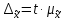 где  – коэффициент кратности средней ошибки выборки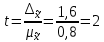 По таблице функции Лапласа определим вероятность:  Вероятность того, что предельная ошибка выборочной средней стоимости покупок на 1 покупателя не превысит 1,6 р., равна 0,954. Выборочная доля покупателей, приобретших товаров на сумму более 60 р. равна:  Средняя ошибка доли:   Предельная ошибка выборки:   По таблице функции Лапласа определим вероятность: Вероятность того, что предельная ошибка частности покупателей, приобретших товаров на сумму более 60 р. не превысит 0,04, равна 0,954. Задача 1.15 Определить вид корреляционной зависимости. Рассчитать параметры уравнения регрессии и определитьтесноту связи между процентом выполнения Нв и среднемесячной ЗП (таблица 5). Таблица 5 Исходные данные по рабочим - сдельщикам
|
