МатематикаВысш№1. Высшая математика (часть 1). Контрольная работа по дисциплине Высшая математика часть 1
 Скачать 104.35 Kb. Скачать 104.35 Kb.
|
|
Федеральное агентство связи федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ) 11.03.02 Инфокоммуникационные технологии и системы связи, профиль Защищённые сети связи (дистанционная форма обучения) Контрольная работа по дисциплине «Высшая математика часть 1» Вариант 10 Выполнила: студент ФАЭС, гр. ЗБТ-22 П.Д. Чмаркова «__»_________ 2022 г. Новосибирск 2022 Оглавление Задание 1. Матричная алгебра Задание 2. Аналитическая геометрия Задание 3. Предел функции Задание 4. Исследование функции Задание 5. Интеграл Задание 6. Функции двух переменных Задание 1: Матричная алгебра  Записываем систему линейных алгебраических уравнений (СЛАУ) в обычном виде, оставляя все неизвестные в левой части, а свободные коэффициенты переносим в правые части:  Записываем СЛАУ в матричной форме: 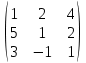 * *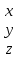 = =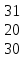 Находим значение главного определителя матрицы СЛАУ. Поскольку оно не равно нулю, СЛАУ имеет единственное решение:   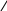 Δ = Δ =  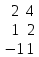 = -27 = 0 = -27 = 0 Находим определитель Δx, полученный из главного определителя путем замены данных в 1 столбце на вектор свободных коэффициентов:   Δx = 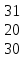 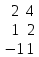 = -27 = -27Находим определитель Δy, полученный из главного определителя путем замены данных в 2 столбце на вектор свободных коэффициентов:   Δy =   = 351 = 351  Находим определитель Δz, полученный из главного определителя путем замены данных в 3 столбце на вектор свободных коэффициентов: Находим определитель Δz, полученный из главного определителя путем замены данных в 3 столбце на вектор свободных коэффициентов:Δz =   = -378 = -378Находим значение переменной x по формуле: x=  = = 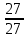 = 1 = 1Находим значение переменной y по формуле: y= 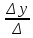 = =  = -13 = -13Находим значение переменной z по формуле: z=  = =  = 14 = 14Задание 3: Предел функции а)  Найти следующий предел: 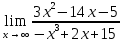 Делим числитель и знаменатель на 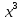  Сокращаем слагаемые  При x        0 0 0 0 0 0 Предел от константы limC =C  Задание 4. Исследование функции Исследование будем проводить по следующей схеме: 1. Найти область определения функции. 2. Найти точки пересечения графика с осями координат. 3. Выяснить, является ли функция чётной, нечётной, периодической или общего вида. 4. Найти точки разрыва функции и определить их характер. 5. Найти асимптоты функции. 6. Найти интервалы монотонности и экстремумы функции. 7. Найти интервалы выпуклости и точки перегиба графика функции. 8. Построить эскиз графика. Область определения: (−∞,−2)∪(−2,∞),{x|x≠−2}(-∞,-2)∪(-2,∞),{x|x≠-2} Диапазон: (−∞,1)∪(1,∞),{y|y≠1} Задание 5. Интеграл Задание 6. Функции двух переменных z =  + +  − x – y − x – yНайти частные производные. Решить систему уравнений 2*x+y3 = 0 3*x*y2 = 0 Получим: а) Из первого уравнения выражаем x и подставляем во второе уравнение: x = 0 y3 = 0 Откуда y = 0 Данные значения y подставляем в выражение для x. Получаем: x = 0 б) Из первого уравнения выражаем y и подставляем во второе уравнение: y1 = 21/3*(-x)1/3 3*22/3*x*(-x)2/3 = 0 или -3*22/3*(-x)5/3 = 0 Или Или Откуда x1 = 0; x2 = 0; x3 = 0 Данные значения x подставляем в выражение для y. Получаем: y1 = 0; y2 = 0; y3 = 0 Количество критических точек равно 2. M1(0;0), M2(0;0) Найти частные производные второго порядка Вычислить значение этих частных производных второго порядка в критических точках M(x0;y0). Вычисляем значения для точки M1(0;0) AC - B2 = 0, то вопрос о наличии экстремума остается открытым. Вычисляем значения для точки M2(0;0 AC - B2 = 0, то вопрос о наличии экстремума остается открытым  |
