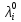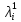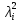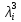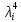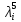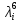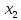Контрольная работа. Раздел Множества
 Скачать 267.44 Kb. Скачать 267.44 Kb.
|
1 2 Контрольная работа. 1. Раздел «Множества» 1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В, С. Продукцию всех трех видов выпускают 10 предприятий, продукцию А и В – 18 предприятий, продукцию А и С – 15 предприятий, продукцию В и С – 21 предприятие. Число предприятий, выпускающих продукцию А равно числу предприятий, выпускающих продукцию В и равно числу предприятий, выпускающих продукцию С. Найти число всех предприятий. Обозначим: 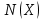 – число элементов множества – число элементов множества 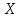 . Обозначим множества: . Обозначим множества: 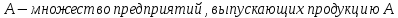 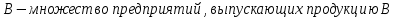 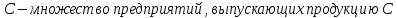 По условию задачи: 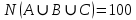 – число всех предприятий (так как каждое предприятие выпускает хотя бы одну продукцию вида А, В, С, то объединение множеств – число всех предприятий (так как каждое предприятие выпускает хотя бы одну продукцию вида А, В, С, то объединение множеств 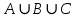 представляет множество всех предприятий фирмы); представляет множество всех предприятий фирмы); 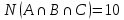 – число предприятий, выпускающих продукцию 3-х видов; – число предприятий, выпускающих продукцию 3-х видов; 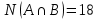 – число предприятий, выпускающих продукцию видов – число предприятий, выпускающих продукцию видов 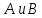 ; ; 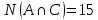 – число предприятий, выпускающих продукцию видов – число предприятий, выпускающих продукцию видов 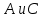 ; ; 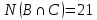 – число предприятий, выпускающих продукцию видов – число предприятий, выпускающих продукцию видов 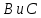 . .Кроме того, дано: 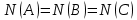 , обозначим это число , обозначим это число 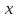 . .Используем формулу включений и исключений для трёх множеств: 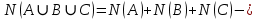 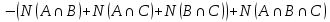 Получаем: 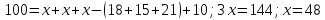 . .Число предприятий, выпускающих хотя бы один из трёх видов продукции равно 48. 2. Упростить: 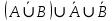 По закону де Моргана, 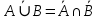 Получаем: 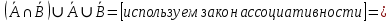 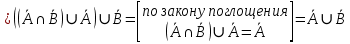 Таким образом, 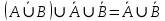 3. Является ли множество 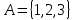 подмножеством множества подмножеством множества 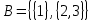 ? ?Множество 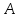 являлось бы подмножеством множества являлось бы подмножеством множества 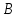 , если бы каждый элемент множества , если бы каждый элемент множества 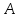 являлся бы элементом множества являлся бы элементом множества 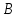 . Возьмём, например, элемент 1 множества . Возьмём, например, элемент 1 множества 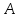 . Этот элемент не принадлежит множеству . Этот элемент не принадлежит множеству 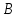 как элемент (множество как элемент (множество 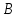 содержит подмножество содержит подмножество 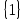 как элемент, но не 1). Следовательно, множество как элемент, но не 1). Следовательно, множество 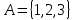 не является подмножеством множества не является подмножеством множества 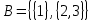 . .4. Придумать пример множеств 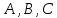 , каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: , каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: 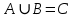 . .Мощность континуума имеет множество, эквивалентное отрезку 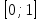 . В качестве множества . В качестве множества 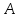 возьмём множество равное этому отрезку: возьмём множество равное этому отрезку: 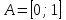 . Возьмём . Возьмём 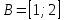 . Тогда взаимно-однозначное соответствие между точками отрезка . Тогда взаимно-однозначное соответствие между точками отрезка 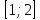 и точками и точками 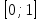 устанавливается линейной функцией устанавливается линейной функцией 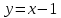 . Значит, множество . Значит, множество 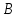 имеет мощность континуума. Возьмём имеет мощность континуума. Возьмём 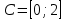 . Тогда взаимно-однозначное соответствие между точками отрезка . Тогда взаимно-однозначное соответствие между точками отрезка 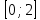 и точками и точками 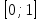 устанавливается линейной функцией устанавливается линейной функцией 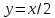 . Значит, множество . Значит, множество 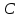 имеет мощность континуума. Все три множества имеет мощность континуума. Все три множества 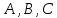 имеют мощность континуума. Равенство имеют мощность континуума. Равенство 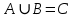 выполняется, очевидно: выполняется, очевидно: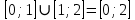 5. Эквивалентны ли множества 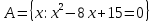 и и 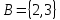 ? ?Определим множество 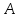 – множество корней квадратного уравнения – множество корней квадратного уравнения 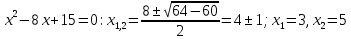 Значит, 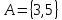 Множества 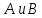 – конечные и содержат одно и то же число элементов (по два элемента). Значит, они эквивалентны – между ними можно установить взаимно-однозначное соответствие. Например, – конечные и содержат одно и то же число элементов (по два элемента). Значит, они эквивалентны – между ними можно установить взаимно-однозначное соответствие. Например, 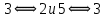 . .2. Раздел «Отношения. Функции» 1. Задано бинарное отношение 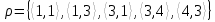 Найти 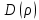 , , 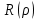 , , 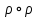 , , 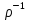 . Проверить, будет ли отношение . Проверить, будет ли отношение 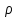 рефлексивным, симметричным, антисимметричным, транзитивным? рефлексивным, симметричным, антисимметричным, транзитивным?Область определения 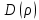 – множество всех первых компонент, фигурирующих в парах отношения – множество всех первых компонент, фигурирующих в парах отношения 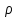 : :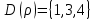 Область значений 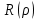 – множество всех вторых компонент, фигурирующих в парах отношения – множество всех вторых компонент, фигурирующих в парах отношения 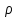 : :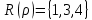 Композиция 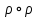 – множество пар – множество пар 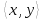 – таких, что существует – таких, что существует 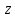 такое, что такое, что 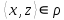 и и 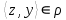 . .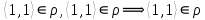 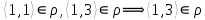 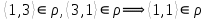 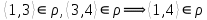 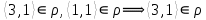 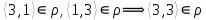 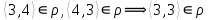 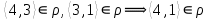 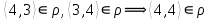 Учитывая каждую пару один раз, определяем композицию: 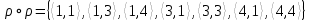 Обратное отношение, по определению: 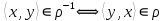 Тогда: 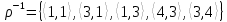 Видим, что обратное отношение совпадает с заданным: 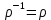 . .Проверить, будет ли отношение 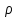 рефлексивным, симметричным, антисимметричным, транзитивным. рефлексивным, симметричным, антисимметричным, транзитивным.Не для любого элемента 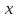 выполняется выполняется 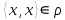 : например, : например, 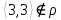 . Значит, отношение . Значит, отношение 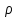 не является рефлексивным. не является рефлексивным.Видим, что для любой пары отношения 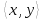 пара пара 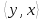 также принадлежит отношению. Значит, отношение также принадлежит отношению. Значит, отношение 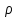 является симметричным. является симметричным.Отношение 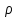 не является антисимметричным: из одновременного выполнения не является антисимметричным: из одновременного выполнения 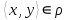 и и 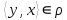 не следует: не следует: 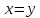 . Например, . Например, 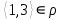 и и 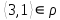 , но , но 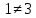 . .Транзитивность отношения: из 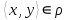 и и 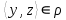 должно следовать должно следовать 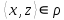 . Это не выполняется, например . Это не выполняется, например 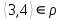 и и 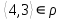 , но , но 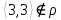 . Значит, отношение . Значит, отношение 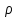 не является транзитивным. не является транзитивным.2. Привести пример отношения не рефлексивного, не симметричного и транзитивного. Рассмотрим бинарное отношение, заданное на множестве 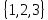 : :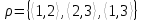 Не для любого элемента 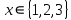 выполняется выполняется 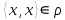 : например, : например, 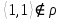 . Значит, отношение . Значит, отношение 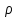 не является рефлексивным. В нашем случае, отношение является антирефлексивным: не является рефлексивным. В нашем случае, отношение является антирефлексивным: 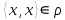 не выполняется ни для какого не выполняется ни для какого 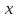 . .Видим, что не выполняется: из 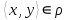 следует следует 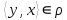 . Например, . Например, 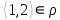 , но , но 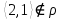 . Значит, отношение . Значит, отношение 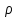 не является симметричным. не является симметричным.Транзитивность: из 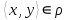 и и 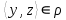 должно следовать должно следовать 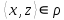 . Это выполняется: . Это выполняется: 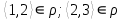 , и , и 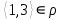 (другие пары отношения “не стыкуются”). Значит, отношение (другие пары отношения “не стыкуются”). Значит, отношение 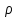 является транзитивным. является транзитивным.Другой пример – отношение “быть старше”, заданное на множестве людей. Ясно, что это отношение не рефлексивно, не симметрично и транзитивно. 3. Дана функция 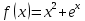 , отображающая множество действительных чисел , отображающая множество действительных чисел 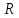 во множество действительных чисел: во множество действительных чисел:  . Является ли эта функция сюръективной, инъективной, биективной? Почему? . Является ли эта функция сюръективной, инъективной, биективной? Почему?Поскольку 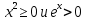 , то функция , то функция 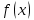 является положительной: является положительной: 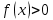 для всех для всех 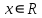 . Тогда не для всех . Тогда не для всех 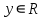 существует существует 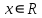 – такое, что – такое, что 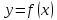 (для (для 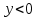 не существует). Значит, функция не существует). Значит, функция 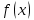 не является сюрьективной. не является сюрьективной.Проверим, является ли функция инъективной. Производная функции: 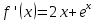 Производная равна нулю при 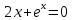 . Это уравнение имеет 1 действительный корень: . Это уравнение имеет 1 действительный корень: 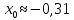 . При . При 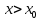 производная положительна и функция монотонно возрастает, при производная положительна и функция монотонно возрастает, при 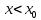 производная отрицательна и функция монотонно убывает: производная отрицательна и функция монотонно убывает: 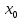 – точка минимума. – точка минимума.График функции: 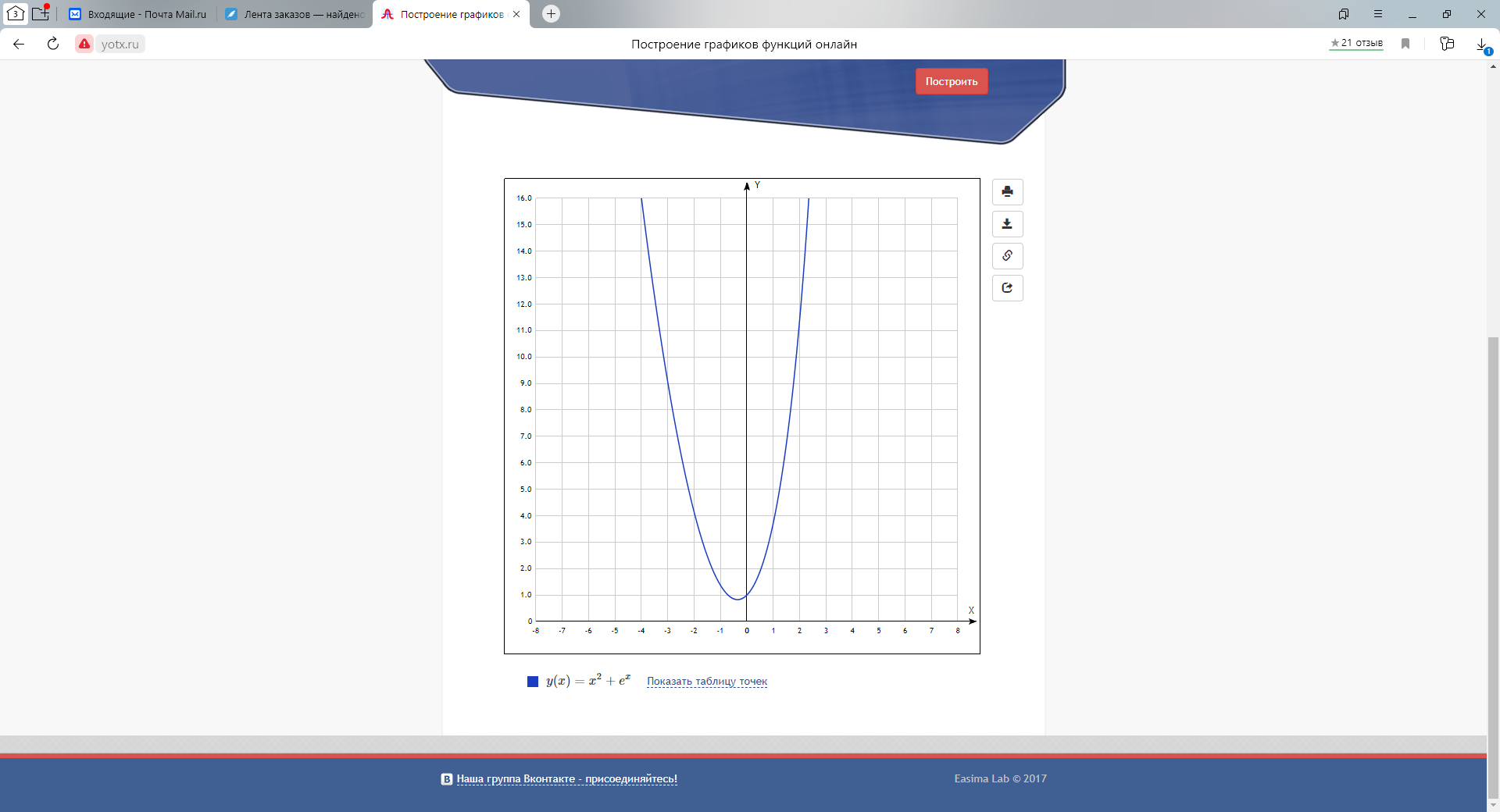 Значит, для любого значения 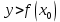 существует два значения существует два значения 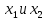 – такие, что – такие, что 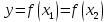 . Значит, функция не является инъективной (инъективная функция переводит любые два разных значения аргумента в разные значения). . Значит, функция не является инъективной (инъективная функция переводит любые два разных значения аргумента в разные значения).Функция 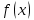 не является биективной (биективная функция является сюръективной и инъективной). не является биективной (биективная функция является сюръективной и инъективной).3. Раздел «Графы» 1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности). 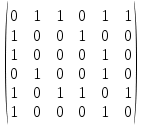 Поскольку матрица смежности является симметричной (элементы симметричны относительно главной диагонали), то заданный граф является неориентированным. Построим граф по заданной матрице смежности. Так как матрица смежности – квадратная матрица порядка 6, то граф имеет 6 вершин. Единице, стоящей на пересечении 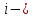 той строки и той строки и 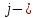 го столбца соответствует ребро, соединяющее вершины го столбца соответствует ребро, соединяющее вершины 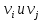 . Граф: . Граф:           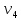      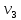      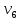 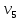 Видим, что заданный граф является связным: между любыми двумя вершинами графа существует путь, связывающий рёбрами эти вершины. Заданный граф не имеет петель (это соответствует тому, что в матрице смежности все элементы по главной диагонали равны нулю). Подсчитаем степени вершин графа (для каждой вершины – число смежных с ней вершин): 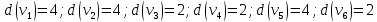 Эйлеров цикл (цикл, проходящий через каждое ребро графа ровно один раз) в графе существует тогда и только тогда, когда выполняются два условия: 1) граф связный; 2) степень каждой вершины чётна. В заданном графе оба эти условия выполняются. Значит, заданный граф является эйлеровым. Эйлеров цикл, например такой: 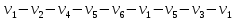 Заданный граф является планарным – мы его построили на плоскости таким образом, что никакие два ребра не пересекаются. Найдём оптимальную раскраску графа. Граф содержит цикл из 3 вершин (треугольник) 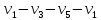 , поэтому наименьшее число цветов, которыми можно раскрасить граф (хроматическое число , поэтому наименьшее число цветов, которыми можно раскрасить граф (хроматическое число 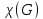 ), должно быть не меньше 3: ), должно быть не меньше 3: 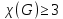 . С другой стороны, раскраску в три цвета в нашем случае можно осуществить. Задаём три цвета вершин треугольника . С другой стороны, раскраску в три цвета в нашем случае можно осуществить. Задаём три цвета вершин треугольника 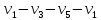 : :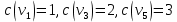 Для остальных трёх вершин задаём цвета: 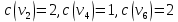 Убеждаемся, что тремя цветами граф раскрашен (любые смежные вершины окрашены в разные цвета). Хроматическое число равно 3: 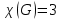 . . Перечислим рёбра графа: 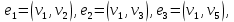 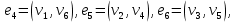 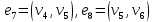 Матрица инцидентности графа содержит имеет 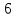 строк (по числу вершин) и строк (по числу вершин) и 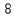 столбцов (по числу рёбер); для ребра столбцов (по числу рёбер); для ребра 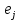 проставляем единицы в проставляем единицы в 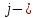 том столбце в строках, соответствующих вершинам ребра том столбце в строках, соответствующих вершинам ребра 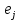 (остальные элементы – нули в этом столбце): (остальные элементы – нули в этом столбце):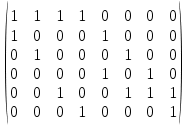 Поскольку заданный граф – неориентированный, то матрица связности совпадает с матрицей сильной связности. Поскольку задан связный неориентированный граф, то из любой вершины можно попасть в любую вершину, значит матрица связности (сильной связности) в нашем случае состоит из всех единиц:  2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из 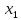 в в 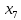 в ориентированном графе, заданном матрицей весов. в ориентированном графе, заданном матрицей весов.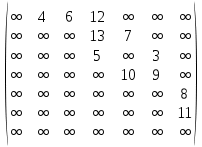 Обозначим: 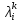 – величина минимального пути, содержащего не более – величина минимального пути, содержащего не более 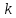 дуг из начальной вершины (в нашем случае дуг из начальной вершины (в нашем случае 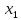 ) в вершину ) в вершину 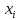 . . Считаем: 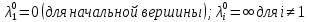 . .Алгоритм Беллмана – Форда выражается формулой: 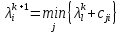 Здесь 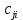 – длина дуги – длина дуги 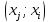 . .Последовательно заполняем таблицу из 7 строк (по строкам - вершины) и 7 столбцов ( 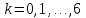 ): ): 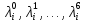 , двигаясь по столбцам. , двигаясь по столбцам.Если в нашем случае 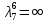 , то пути из , то пути из 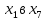 нет; если нет; если 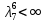 , то это значение даёт величину минимального пути из , то это значение даёт величину минимального пути из 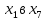 . Определяя изменение . Определяя изменение 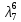 по 7-й строке, последовательно определяем и сам путь (от конца к началу). по 7-й строке, последовательно определяем и сам путь (от конца к началу).Таблица  : :
В первой строке таблицы все значения – нули ( 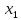 – стартовая вершина). В первом столбце все значения (за исключением первого) равны – стартовая вершина). В первом столбце все значения (за исключением первого) равны 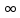 . . Второй столбец (за исключением 1-го значения) соответствует первой строке матрице дуг, так как все пути длины 1 из стартовой вершины соответствуют дугам из неё. Поскольку в вершины 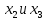 можно попасть только из вершины можно попасть только из вершины 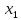 (путь из одной дуги), то значения из 2-го столбца для этих вершин переносим во все остальные столбцы. (путь из одной дуги), то значения из 2-го столбца для этих вершин переносим во все остальные столбцы.Заполняем 3-й столбец – минимальные пути не более чем из 2 дуг. Для 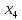 : в эту вершину можно попасть (смотрим на матрицу весов) из вершин : в эту вершину можно попасть (смотрим на матрицу весов) из вершин 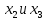 (кроме (кроме 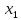 ) и длина пути ) и длина пути 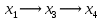 (равная 11) меньше (равная 11) меньше 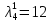 , тогда устанавливаем , тогда устанавливаем 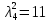 . Для . Для 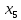 : смотрим на матрицу весов – в эту вершину можно попасть вершин : смотрим на матрицу весов – в эту вершину можно попасть вершин 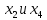 ; из второго столбца таблицы видим, что 4+7 < 12+10 – присваиваем ; из второго столбца таблицы видим, что 4+7 < 12+10 – присваиваем 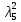 значение 11 (путь значение 11 (путь 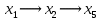 ). Для ). Для 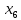 : смотрим на матрицу весов – в эту вершину можно попасть вершин : смотрим на матрицу весов – в эту вершину можно попасть вершин 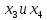 ; из второго столбца таблицы видим, что 6+3 < 12+9 – присваиваем ; из второго столбца таблицы видим, что 6+3 < 12+9 – присваиваем 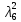 значение 9 (путь значение 9 (путь 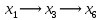 ). Значение ). Значение 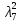 остаётся таким же как и остаётся таким же как и 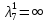 , так как в , так как в 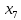 можно попасть только из вершин можно попасть только из вершин 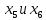 , а для строк 5-й и 6-й во втором столбце стоит , а для строк 5-й и 6-й во втором столбце стоит 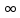 . .Заполняем 4-й столбец – минимальные пути не более чем из 3 дуг. Для 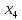 : в эту вершину можно попасть только из вершин : в эту вершину можно попасть только из вершин 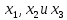 , но для этих вершин значения , но для этих вершин значения 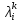 уже не могут поменяться, поэтому значения из 3-го столбца для уже не могут поменяться, поэтому значения из 3-го столбца для 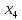 переносим во все остальные столбцы. Для переносим во все остальные столбцы. Для 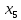 : смотрим на матрицу весов – в эту вершину можно попасть вершин : смотрим на матрицу весов – в эту вершину можно попасть вершин 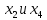 ; из 3-го столбца таблицы видим, что 4+7 < 11+10, поэтому значение ; из 3-го столбца таблицы видим, что 4+7 < 11+10, поэтому значение 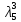 переносится из переносится из 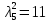 . Для . Для 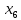 : смотрим на матрицу весов – в эту вершину можно попасть вершин : смотрим на матрицу весов – в эту вершину можно попасть вершин 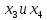 ; из 3-го столбца таблицы видим, что 6+3 < 11+9, поэтому значение ; из 3-го столбца таблицы видим, что 6+3 < 11+9, поэтому значение 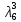 переносится из переносится из 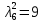 . Для . Для 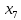 : смотрим на матрицу весов – в эту вершину можно попасть вершин : смотрим на матрицу весов – в эту вершину можно попасть вершин 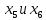 ; из 3-го столбца таблицы видим, что 11+8 < 9+11, поэтому значение ; из 3-го столбца таблицы видим, что 11+8 < 9+11, поэтому значение 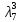 устанавливаем: устанавливаем: 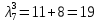 (путь (путь  ). ).Теперь все значения в 4-м столбце заполнены (конечными числами). Поскольку в конечную вершину 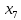 можно попасть только из вершин можно попасть только из вершин 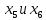 , а значения для этих вершин уже были перенесены из 3-го столбца, то дальнейшее обновление значений (уменьшение) для следующих столбцов уже невозможно, поэтому можно продублировать значения 4-го столбца для следующих столбцов. , а значения для этих вершин уже были перенесены из 3-го столбца, то дальнейшее обновление значений (уменьшение) для следующих столбцов уже невозможно, поэтому можно продублировать значения 4-го столбца для следующих столбцов.Таблица заполнена. Минимальный путь из вершины 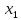 в вершину в вершину 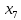 длиной 19: длиной 19:  . .3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер. 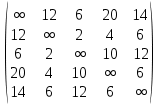 Задан полный неориентированный граф (каждая вершина связана ребром с каждой другой вершиной, как видим по матрице). Построим граф:    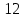 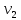 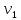                         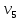 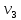     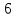 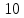  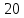   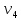 Для построения остовного дерева минимального веса используем алгоритм Краскала. Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса. У нас 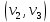 - ребро с минимальным весом 2 – включаем его в остовное дерево: - ребро с минимальным весом 2 – включаем его в остовное дерево: 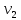    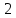   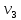 Из оставшихся рёбер минимальный вес равный 4 имеет ребро 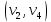 – включаем его в остовное дерево: – включаем его в остовное дерево: 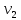   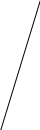  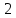   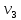     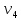 Из оставшихся рёбер минимальный вес равный 6 имеют ребра 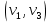 , , 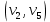 и и 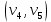 . Если включить все эти три ребра, то образуется цикл . Если включить все эти три ребра, то образуется цикл 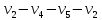 , поэтому сразу три ребра включить нельзя. Если включить ребра , поэтому сразу три ребра включить нельзя. Если включить ребра 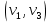 и и 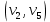 , то циклов не образуются, кроме того добавляются новые вершины , то циклов не образуются, кроме того добавляются новые вершины 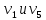 – поэтому можно включить оба этих ребра в остовное дерево: – поэтому можно включить оба этих ребра в остовное дерево:  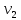 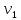                    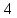   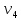 Видим, что все вершины включены в связный граф - остовное дерево минимального веса построено, его вес равен 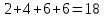 . . 1 2 |