Главная страница
Навигация по странице:

  • Независимые циклы-множество, содержащее все простые циклы(контуры) этого графа

  • 31. Известно, что для раскраски вершин n,m-графа (n фиксировано) использовано два цвета. Является ли данный граф деревом

    		•

    Теория графов


    Скачать 6.88 Mb.
    НазваниеТеория графов
    Анкорdiskra
    Дата28.04.2022
    Размер6.88 Mb.
    Формат файлаdocx
    Имя файлаdiskra_zadachi_po_tg.docx
    ТипДокументы
    #502183

    Раздел 4. Теория графов

    Граф – это графическое изображение специального бинарного отношения .

    Неограф- множество U включает только рёбра

    Инцидентность-бинарное отношение, принадлежность в отношении ребра или дуги и вершин

    Локальная степень(валентность)- числовая характеристика вершины, определенная кол-вом инцидентных ребер

    Орграф-множество U включает только дуги

    Граф со смешанной структурой-множество включает и ребра и дуги

    1. Задан граф G(X,U). Определите, какое из приведенных специальных бинарных от-ношений изображено в виде данного графа.





    2. Задана матрица смежности графа G(X,U). Определите, к какому классу по струк-туре относится данный граф.





    3. Задан граф G(X,U). Определите, к какому виду относится данный граф:

    · псевдограф · полный

    · мультиграф · регулярный

    · скелетный · насыщенный

    · пустой · взвешенный



    Псевдограф-любой бинарный граф

    Мультиграф-граф без петель

    Скелетный граф- мультиграф без кратгыхребёр и дуг

    Пустой – только вершины, дуг нет

    Полный граф- скелетный неограф, в котором все вершины соединены ребром

    Насыщенный граф- полный граф с петлями над каждой вершиной

    Регулярный граф- у всех вершин одинаковые характеристики

    Взвешенный граф- граф, где есть вес над рёбрами

    4. Задан граф G(X,U). Определите смежные вершины, ребра, дуги графа.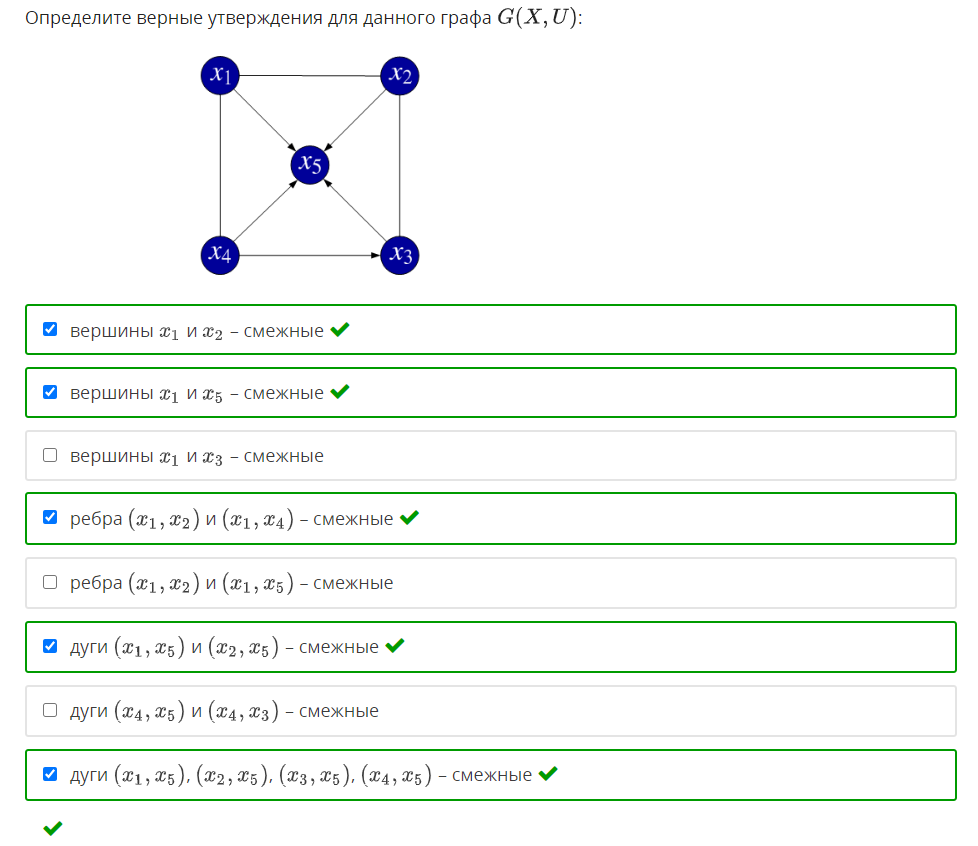



    Смежные вершины, если они являются концами одного и того же ребра или началом и концом одной и той же дуги.

    Ребра смежные, если у них один общий конец

    Кратные ребра, если два общих конца

    Дуги смежные, если у них общая вершина конца дуги.

    5. Заданы n1,m1-граф G1 и n2,m2-граф G2. Определите, сколько вершин содержит n,m-граф, полученный в результате произведения графов G1 и G2.



    Вершины перемножаться. Если в первом графе было 2 вершины, а во втором 3, то в результате их будет 6.

    6. Задан неограф G(X,U). Найдите простые цепи в данном графе.

    Маршрут-упорядоченная последовательность ребер, в которой каждая пара вершин смежна между собой.

    Цепь- маршрут, в котором все ребра различны.

    Простая цепь-цепь, в которой все вершины различны.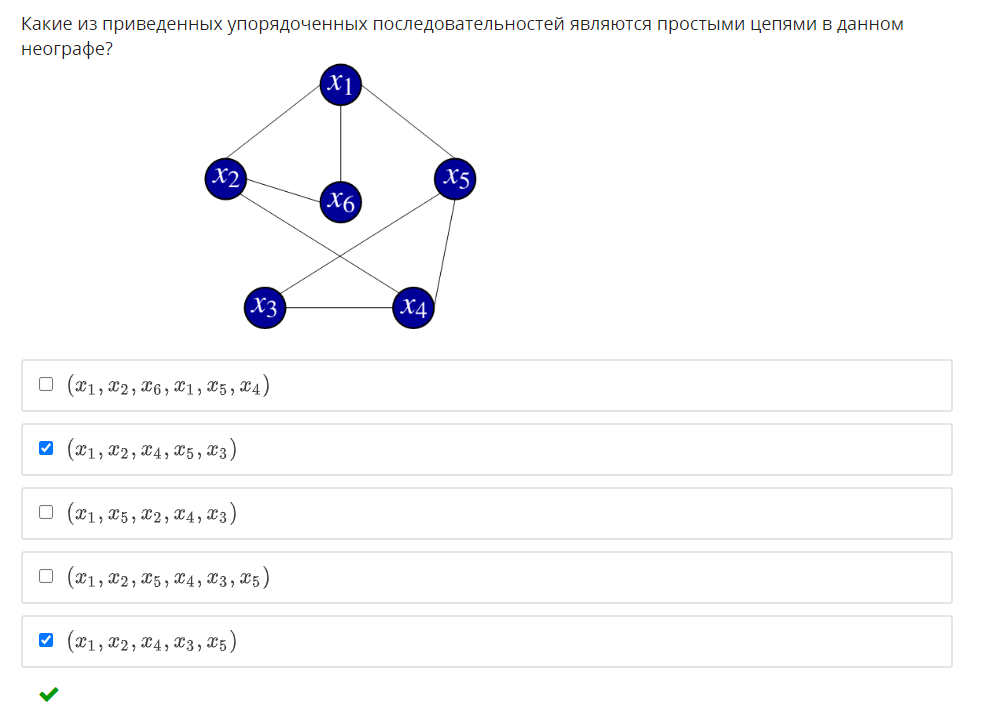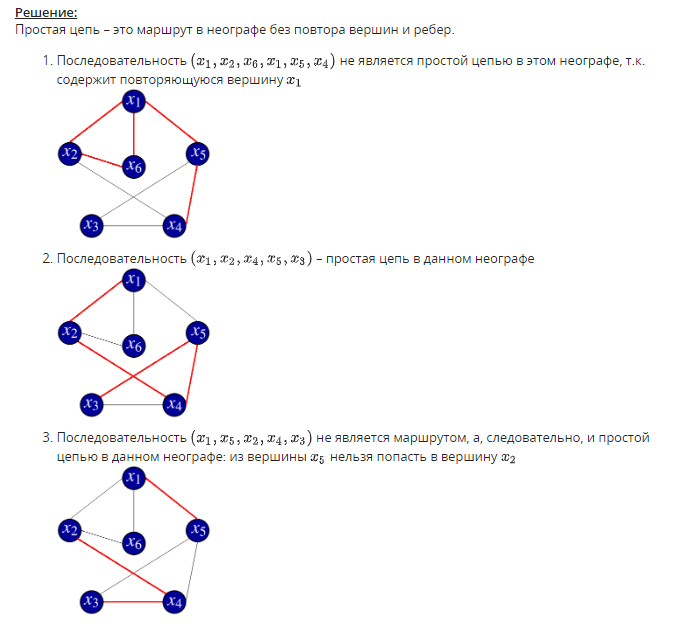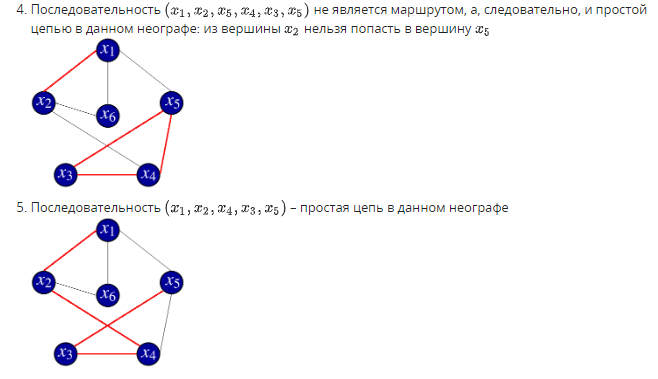



    7. Задан неограф G(X,U). Найдите ребро, которое является мостом в данном графе.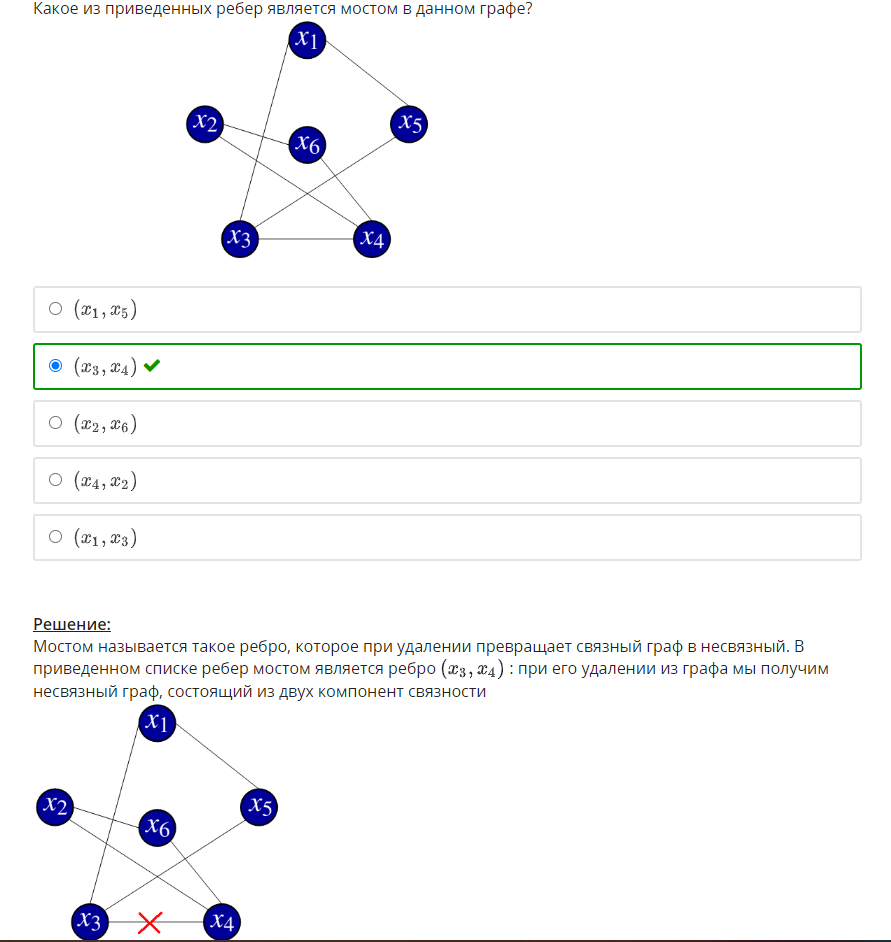



    8. Задан орграф G(X,U). Найдите простые пути в данном графе.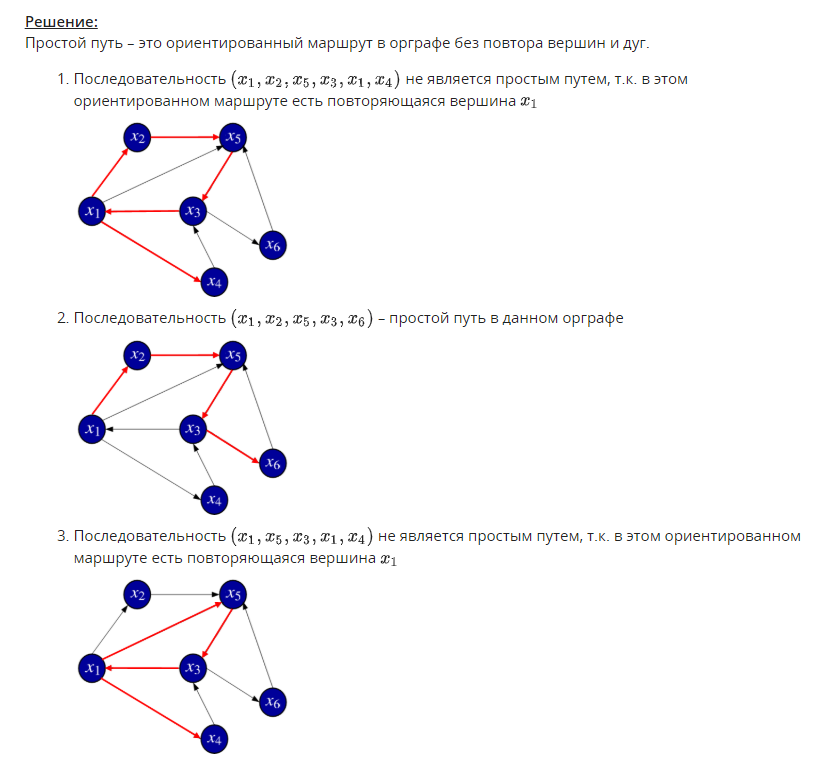







    9. Задан орграф G(X,U). Определите, к какому виду по связности относится данный граф:

    · сильносвязный · слабосвязный · односторонне связный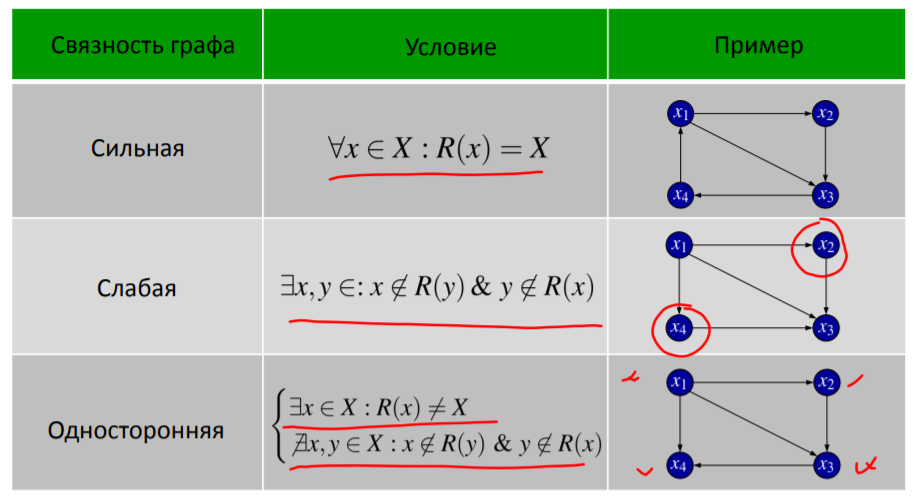





    10. Задан орграф G(X,U). Определите подмножества вершин, порождающие сильные подграфы в данном графе.







    11. Задан неограф G(X,U). Определите, длина какого маршрута определяет эксцентри-ситет вершины xj в этом графе.

    12. Задан неограф G(X,U). Определите простые циклы в данном графе.

    Цикл-замкнутая цепь в неографе

    Простой цикл-замкнутая простая цепь в неографе.





    13. Задан орграф G(X,U). Найдите простые контуры и полуконтуры в данном графе.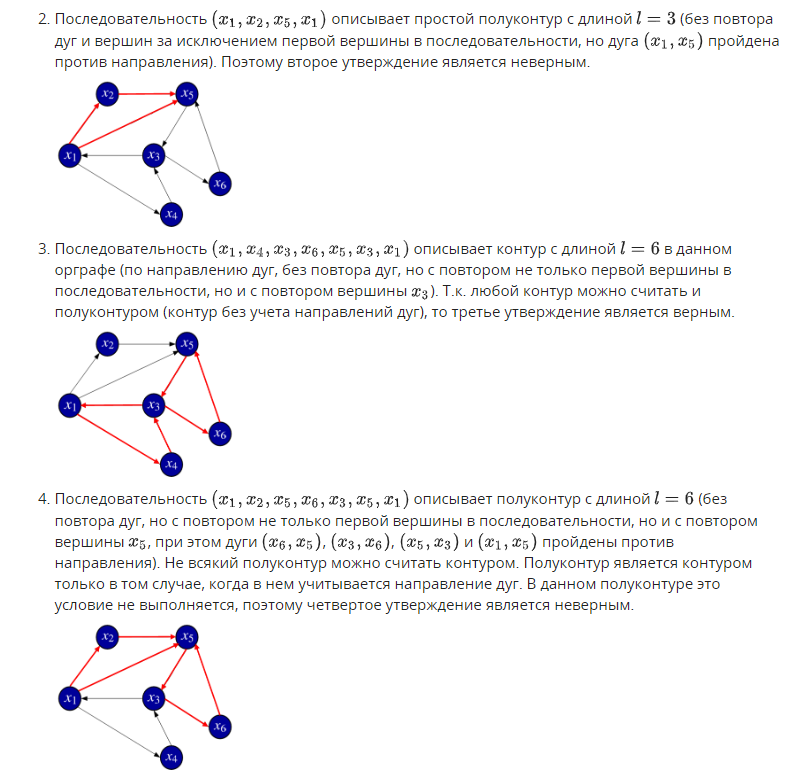





    Контур(ориентированный цикл)-замкнутый путь в орграфе.

    Простой контур-замкнутый простой путь в орграфе.

    Полуконтур-контур, построенный в орграфе без учета направления дуг.

    Просто полуконтур-простой контур, построенный в орграфе без учета направления дуг.

    14. Задан неограф G(X,U). Определите, какие циклы данного графа являются независимыми.

    Независимые циклы-множество, содержащее все простые циклы(контуры) этого графа.

    15. Задан неограф G(X,U). Определите, является ли данный графом Эйлера (полуэйлеровым графом).

    16. Задан неограф G(X,U), не являющийся графом Эйлера. Укажите, какое ребро в него надо добавить, чтобы он стал графом Эйлера.

    17. Задан неограф G(X,U), не являющийся полуэйлеровым графом. Укажите, какие ре-бра из него надо удалить, чтобы он стал полуэйлеровым графом.



    18. Задан неограф G(X,U). Определите, является ли данный графом Гамильтона (полу-гамильтовым графом).

    19. Задан неограф G(X,U), не являющийся графом Гамильтона. Укажите, какое ребро в него надо добавить, чтобы он стал графом Гамильтона.

    20. Задан неограф G(X,U), не являющийся полугамильтоновым графом. Укажите, ка-кие ребра из него надо удалить, чтобы он стал полугамильтоновым графом.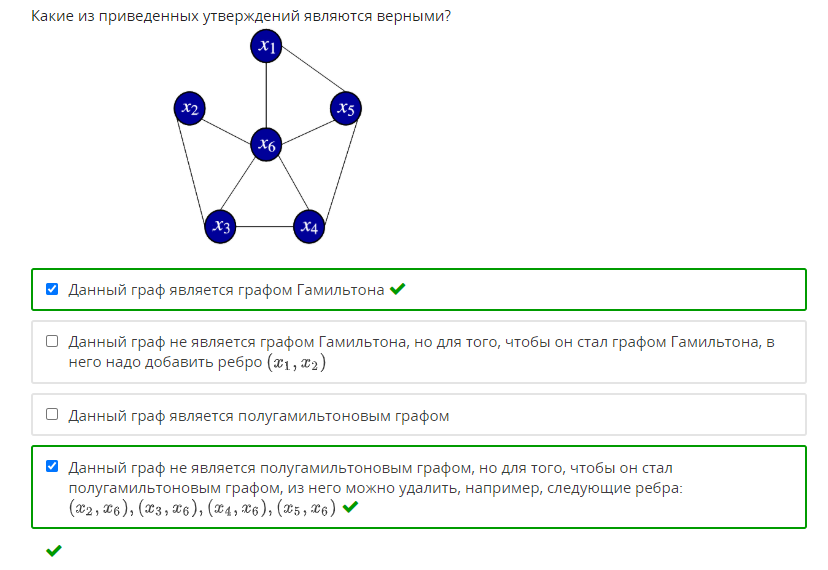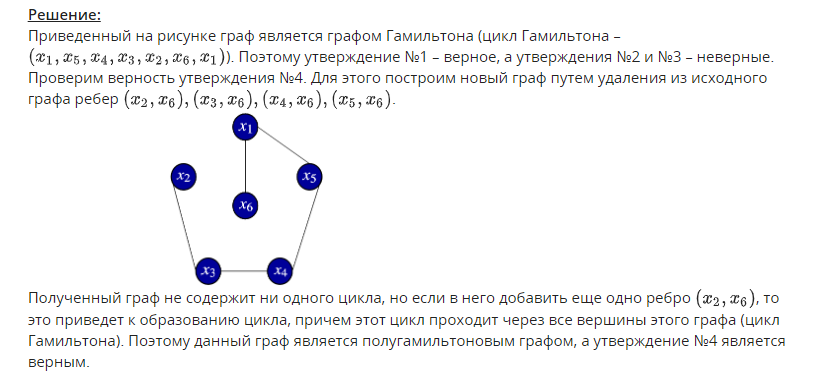



    21. Заданы неографы. Укажите, какие из них являются деревьями.



    22. Задан неограф. Укажите, какие из приведенных деревьев являются суграфом для данного графа.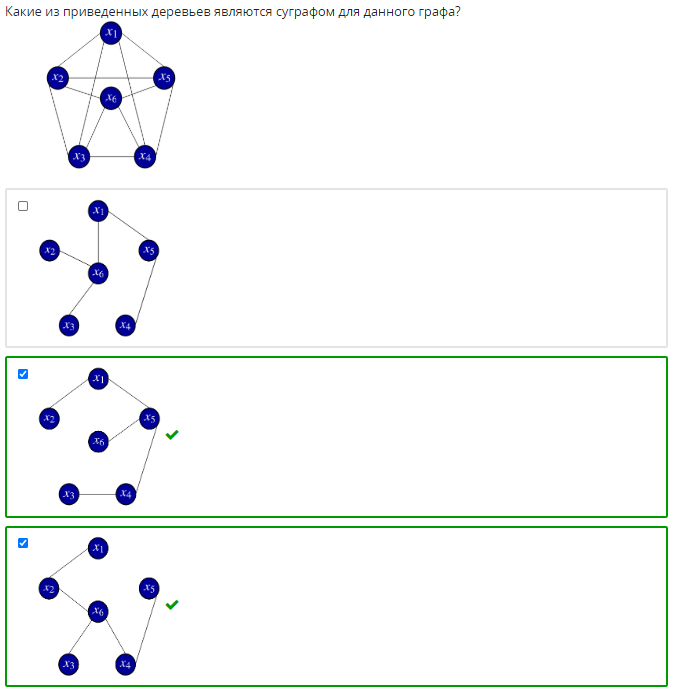





    23. Задан неограф и его остовное дерево. Определите, каким из методов построено это дерево:

    · методом обхода вершин вглубь · методом обхода вершин вширь





    24. Заданы неографы. Укажите среди них корневые деревья.





    25. Бинарное дерево задано списками левых и правых сыновей вершин. Определите, является ли оно полным.

    26. Бинарное дерево представлено списками левых и правых сыновей вершин. Опреде-лите его высоту.

    27. Бинарное дерево представлено списками левых и правых сыновей вершин. Опреде-лите глубину и высоту его xj вершины.

    Через список строим рисунок(левый и правый сын)

    Высота дерева=высота корня





    28. Укажите верные утверждения:

    1) Цикломатическое число любого дерева равно нулю

    2) Цикломатическое число полного n,m-графа равно (n2−3n)/2+1

    3) Цикломатическое число полного n,m-графа равно (n2−3n+1)/2.

    4) Цикломатическое число графа Эйлера всегда больше нуля.

    5) Цикломатическое число полуэйлерова графа всегда больше нуля.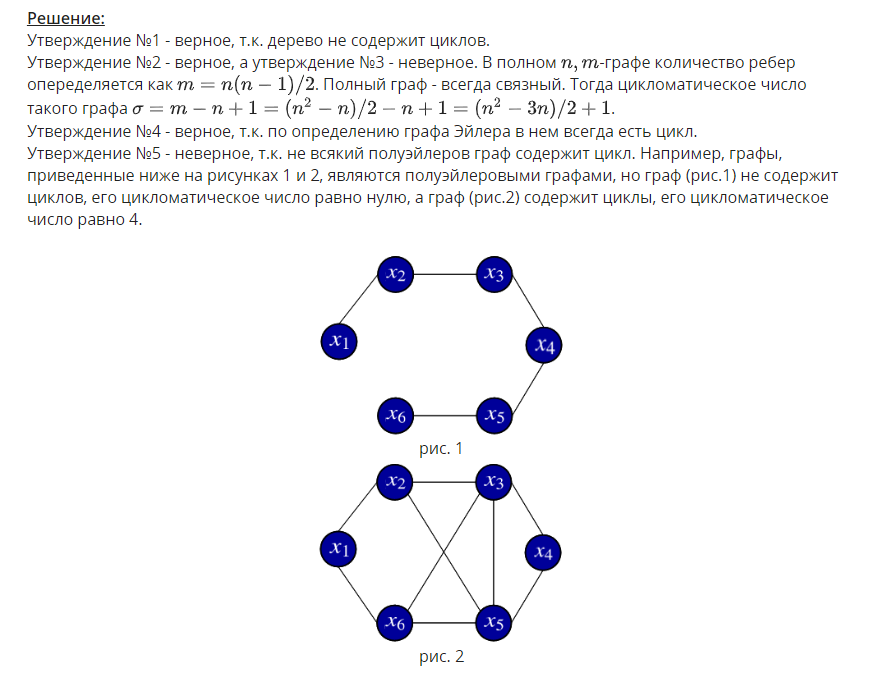





    29. Укажите верные утверждения:

    1. В связном графе при n⩾3 количество вершин, у которых локальная сте-пень ρ(х)=1, определяет верхнюю границу числа внутренней устойчивости этого графа.

    2. В связном графе при n⩾3 количество вершин, у которых локальная сте-пень ρ(х)=1, определяет нижнюю границу числа внутренней устойчивости этого графа.

    3. В связном графе при n⩾3 количество вершин, у которых локальная сте-пень ρ(х)=1, определяет число внутренней устойчивости этого графа.



    30. Известно, что число внутренней устойчивости связного графа равно к. Определите кликовое число его графа-дополнения.




    31. Известно, что для раскраски вершин n,m-графа (n фиксировано) использовано два цвета. Является ли данный граф деревом?

    32. Для раскраски вершин n,m-графа (n фиксировано) использовано два цвета. Определите число внутренней устойчивости этого графа.



    33. Граф G(X,U) задан матрицей смежности. Укажите число внешней устойчивости этого графа.







    34. Заданы неографы. Укажите, какие из них являются двудольными.





    35. Задан гиперграф H(X,R). Определите количество вершин n(K) и количество бинар-ных рёбер m(K) Кёнигова представления K(H) данного гиперграфа.







    36. Задан гиперграф H(X,R). Определите цепь, цикл в данном гиперграфе.





    37. Задан гиперграф H(X,R). Определите, сколько гиперрёбер содержит подгипер-граф H′(X′,R′), порожденный в данном гиперграфе множеством вершин X′.



    38. Два графа заданы матрицами смежности M1 и M2. Определите, выполняются ли все необходимые условия для их изоморфизма.



    Теория для след вопросов:



    39. Задан плоский граф. Определите количество граней в графе f и количество граней, которым принадлежит фиксированная точка «a».

    40. Задан связный плоский n,m-граф. Определите количество его граней.





    41. Задан связный планарный n,m-граф (n фиксировано). Определите максимальное количество ребер в графе:

    · Если граф является двудольным

    · Если граф не является двудольным



    42. Задан граф Петерсена. Укажите, к какому графу можно его стянуть:

    · только к графу K5.

    · только к графу K3,3.

    · и к графу K5, и к графу K3,3.







    А
    нимация: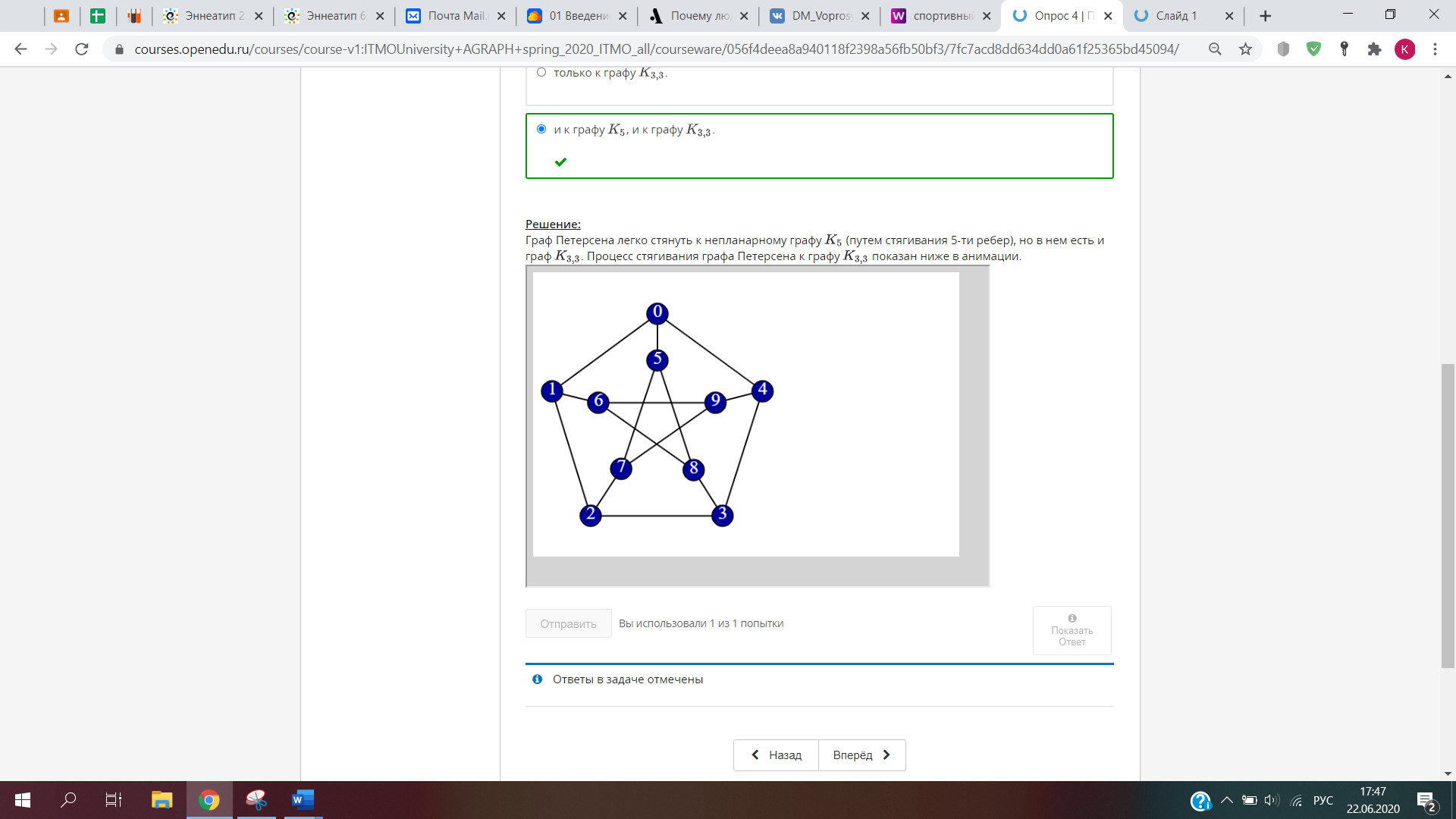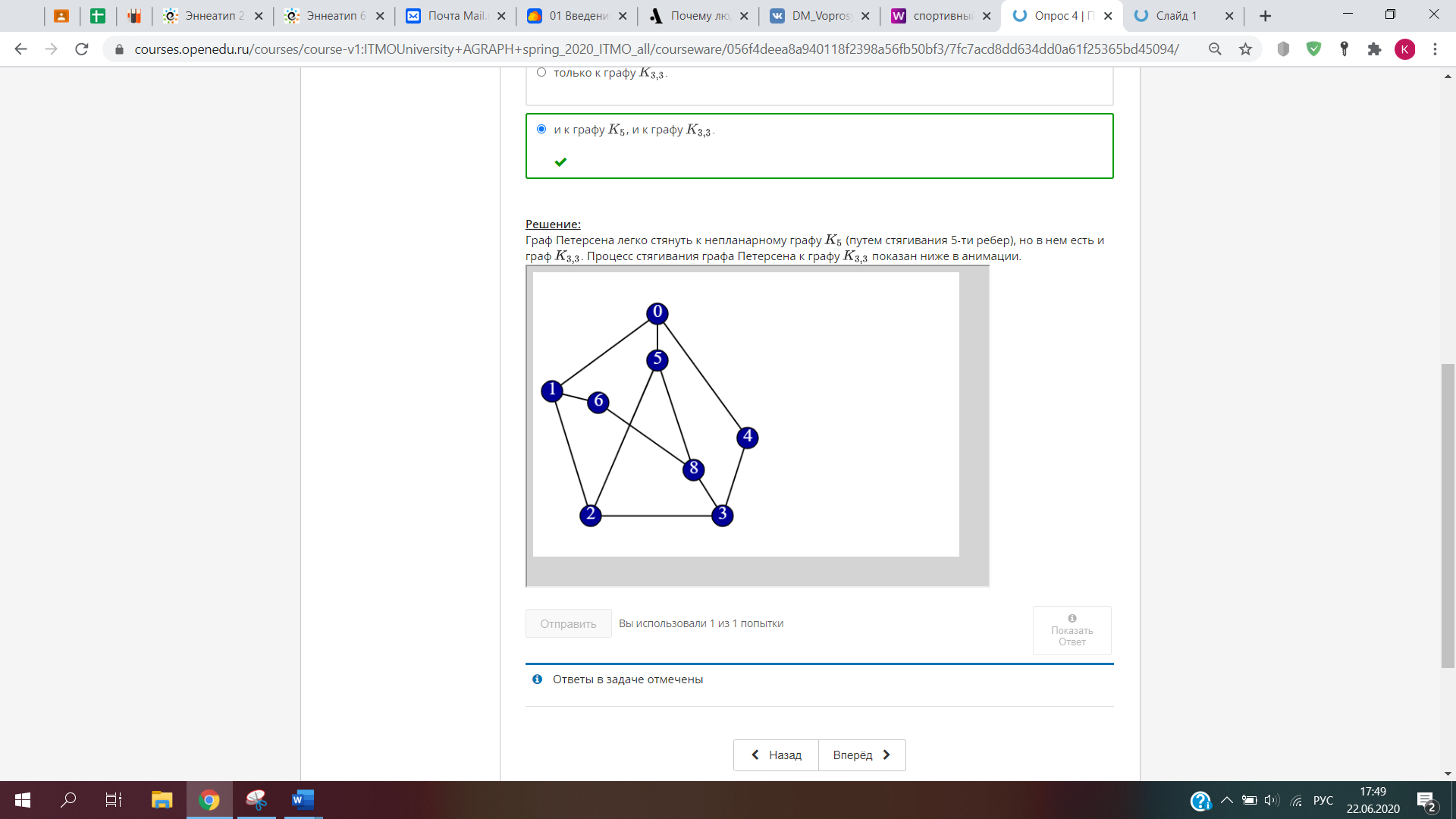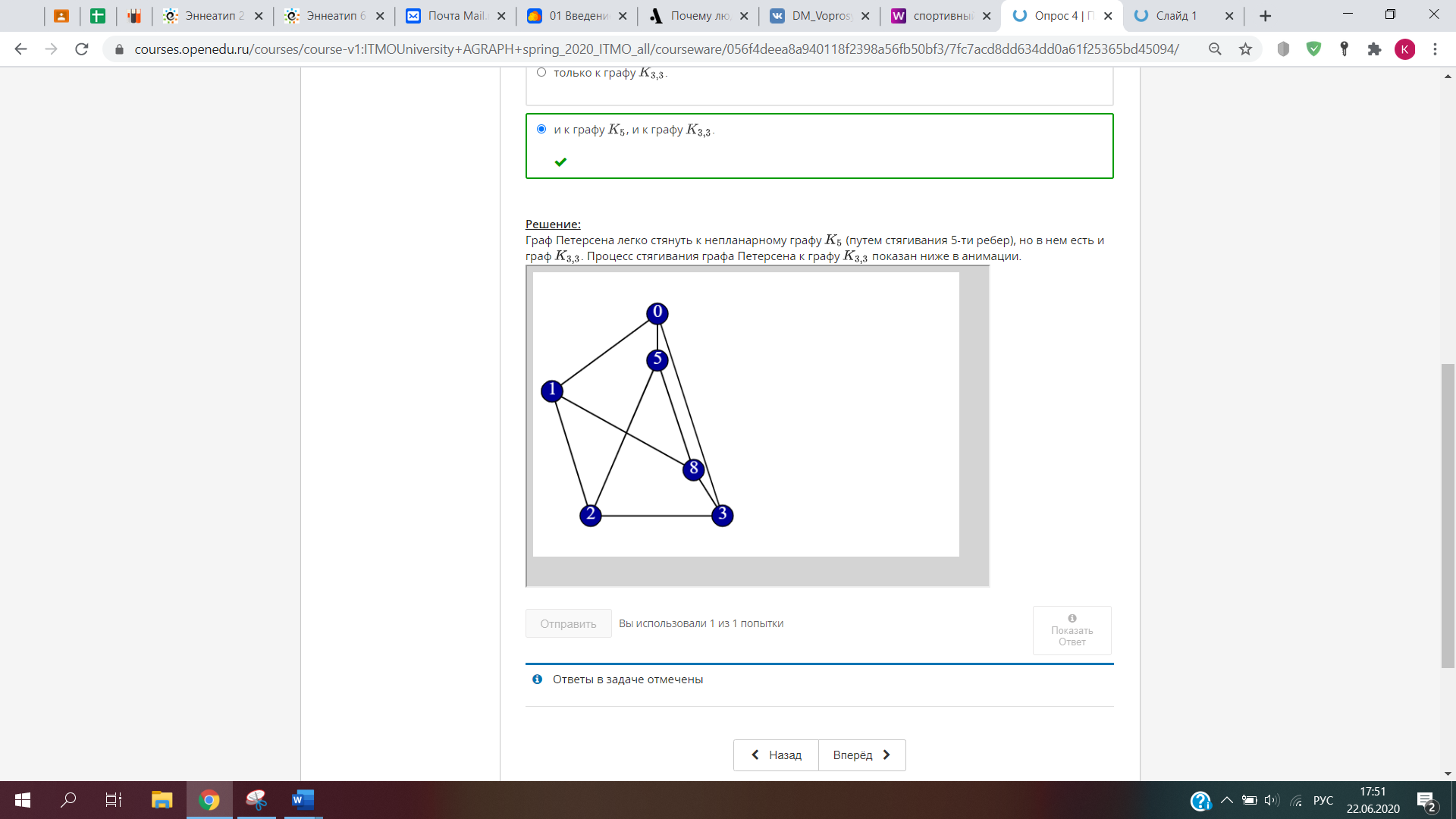

    написать администратору сайта