математика. Конттольн рб по матем. Контрольная работа (
 Скачать 32.13 Kb. Скачать 32.13 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» (УрГЭУ) КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Тема: Контрольная работа (вариант 5)
Екатеринбург 2023 г. 2 Семестр Тема 1. Элементы комбинаторики. События и их вероятности, классический и геометрический способы подсчета вероятностей Вариант 5. Товаровед получил 50 одинаковых изделий, среди них 5 бракованных. Наудачу для контроля взяты путём случайного выбора три изделия. Найти вероятность того, что среди них окажется ровно одно бракованное. Решение: Число всех возможных исходов испытания n = 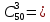 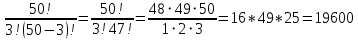 Событие А {из 3-х изделий одно изделия бракованное} Число исходов, благоприятствующих событию А: m = 1 → 3 - 1=2 (стандартных) 50 – 5 = 45(стандартных) 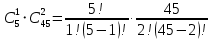 = =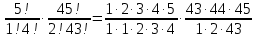 = 5 ∙ 990=4950 = 5 ∙ 990=4950P(A) = 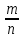 = = 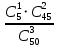 = = 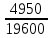 = 0.253 = 0.253Ответ: вероятность того, что среди 3-х изделий одно бракованное равна 0.253 Тема 2. Операции над событиями. Правила сложения и умножения вероятностей Вариант 5. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трёх проверенных изделий только два изделия высшего сорта. Решение: Пусть события А1 = {первое изделия высшего сорта} А2 = {второе изделия высшего сорта} А3 = {третье изделия высшего сорта} A = {только два изделия из трех проверенных высшего сорта} Появление события A означает, что наступило одно из трёх несовместных событий: либо 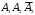 , либо , либо 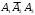 , либо , либо 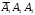 . .P(A̅) = 1 – P(A) = 1 – 0,8 = 0,2 P(A̅1A2A3) = P(A̅1) ∙ P(A2) ∙P(A3) = 0,2 ∙ 0,8 ∙ 0,8 = 0,128 P(A1A̅2A3) = P(A1) ∙ P(A̅2) ∙P(A3) = 0,8 ∙ 0,2 ∙ 0,8 = 0,128 P(A1A2A̅3) = P(A1) ∙ P(A2) ∙P(A̅3) = 0,8 ∙ 0,8 ∙ 0,2 = 0,128 Тогда Р(А) = 0,128 + 0,128 + 0,128 = 0,384 Ответ: вероятность того, что из трех проверенных изделий только два изделия высшего сорта равна 0,384 Тема 3. Формула полной вероятности. Формулы Бейеса Вариант 5. Известно, что в партии из 600 электрических лампочек 200 изготовлены на первом заводе, 250 на втором, 150 – на третьем. Вероятности того, что лампочка окажется стандартной при изготовлении на первом, втором, третьем заводах соответственно равны 0,97, 0,91 и 0,93. Какова вероятность того, что взятая наудачу лампочка окажется стандартной, изготовлена вторым заводом? Решение: Событие А = {лампочка окажется стандартной} Гипотеза H1 – лампочка изготовлена на первом заводе, Гипотеза Н2 – лампочка изготовлена на втором заводе, Гипотеза Н3 – лампочка изготовлена на третьем заводе. Находим вероятность данных гипотез: Р(Н1) = 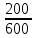 = = 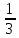 ≈ 0,33; Р(Н2) = ≈ 0,33; Р(Н2) = 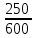 = = 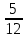 ≈ 0,42; Р(Н3) = ≈ 0,42; Р(Н3) = 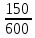 = 0,25 = 0,25РН1(А) = 0,97; РН2(А) = 0,91; РН3(А) = 0,93 Подставляем в формулу полной вероятности → Р(А) = Р(Н1) ∙РН1(А)+Р(Н2) ∙РН2(А)+…+Р(Нn) ∙РНn (А) Р(А) = Р(Н1) ∙РН1(А)+Р(Н2) ∙РН2(А)+ Р(Н3) ∙РН3(А) Р(А) = 0,33∙0,97+0,42∙0,91+0,25∙0,93 = 0,3201+0,3822+0,2325 = 0,9348 Т.к. событие А уже произошло подставляем в формулу Бейеса. Р(А) = 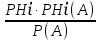 Р(А) = 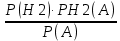 = = 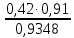 = = 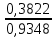 ≈ 0,409 ≈ 0,409Ответ: вероятность того, что взятая наудачу лампочка окажется стандартной, изготовлена вторым заводом равна 0,409 Тема 4. Повторение независимых испытаний. Наивероятнейшее число успехов. Формулы Бернулли, Лапласа, Пуассона. Вариант 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов ровно 5000. Решение: Т.к. число событий n = 5000 велико, а вероятность каждого события мала p = 0,001 законом сходится к закону распределения Пуассона. λ = n ∙ p = 5000 ∙ 0.001 = 5 → 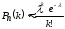 P(k≥2) = 1 - P (k <2) = 1- (P (0) + P (1)); P (0) = 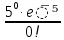 = = 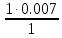 = 0.007; = 0.007; P (1) = 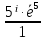 = = 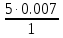 = 0.035; = 0.035;Тогда искомая вероятность P(k≥2) = 1 - (0,007+0,035) = 0,958 Ответ: вероятность попадания в цель двух и более пуль, при 5000 выстрелов равна 0,958 |
