Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры

• Название: Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры
• Дата: 01.02.2022
• Размер: 7.1 Mb.
• Имя файла: analiz_dannykh.docx
• Тип: Документы; #348213
• страница: 1 из 4

1. 
   Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры.
   

Равновозможные события– это события такие, что ни одно из них не является более возможным, чем другие (например:кубику всё равно на какую грань упасть).

Совместные события– это события, которые могут произойти одновременно в результате данного опыта. (например:бросаем 2 кубика - выпадение числа 1 и выпадение числа 3 – совместные события).

Несовместные события– это равновозможные события такие, что появление одного из них исключает появление остальных.(например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).

Несколько случайных событий:    образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).

Противоположные события   – это равновозможные несовместные события, образующие полную группу событий. Появление события   исключает появление события   . ( например: орёл или решка, попадание в мишень или промах).
Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.

Вероятность события   – это отношение числа исходов, благоприятствующих данному событию (m), к общему числу всех несовместных и равновозможных исходов данного опыта (n).

П
ример. Какова вероятность выпадения четного числа очков при бросании игральной кости?

С
войства вероятности:

• 
  Вероятность достоверного события равна единице.
  
• 
  Вероятность невозможного события равна нулю.
  
• 
  Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
  

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

• 
  0 ≤ P(A) ≤ 1.
  

Непосредственный подсчёт вероятности событий с использованием классического определения вероятности.

При решении задач на непосредственный подсчёт вероятности с использованием записанной формулы нет общих способов для нахождения чисел m и n. Часто для их нахождения используют комбинаторику (число размещений, перестановок, сочетаний).

Пример 1. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковые? Решение.

Пусть А - событие, заключающееся в том, что в наудачу выбранном двузначном числе цифры одинаковые.

где n - число двузначных чисел (двузначные числа 10-99, всего их 90), m - количество чисел, имеющих одинаковые цифры (таких чисел 9, это - 11, 22, 33, 44, 55, 66, 77, 88, 99). Следовательно: P(A) = 9/90=0,1

2. 
   Использование комбинаторики для вычисления вероятностей. Пример.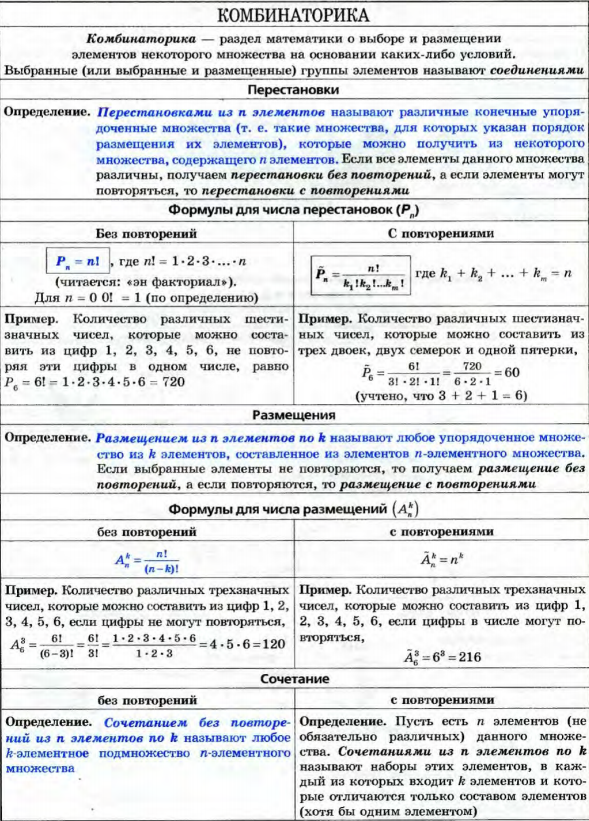
   

2. 
   Несовместные и совместные события. Сумма событий. Теоре­ма сложения вероятностей (с доказательством). Пример.
   

Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.

2 события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Аналогично суммой конечного числа событий А₁, А₂, ..., А_kназывается событие А = А₁+А₂ + ... + А_k, состоящее в наступлении хотя бы одного из событий Аi, (i = 1, ..., k). Из определения следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А + А = А (а не 2А).

Теорема сложения вероятностей:

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий: Р(А + В + ... + К) = Р(А) + Р(В) + ... + Р(К).

□ Докажем теорему для схемы случаев, рассматривая сумму двух событий.

Пусть в результате испытания из общего числа n равновозможных и несовместных (элементарных) исходов испытания (случаев) событию А благоприятствует m_l случаев, а событию В ­ m₂ случаев (рис. 1.4).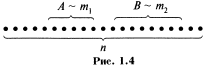



Согласно классическому определению  .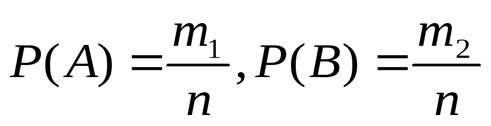

Т.к. события А и В несовместные, то ни один из случаев, благоприятствующих одному из этих событий, не благоприятствует другому (рис. 1.4). Поэтому событию А+В будет благоприятствовать m_l + m₂ случаев. Следовательно,  ■

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна 1:

P(A) + P(B) + … + P(K) = 1.

□ Если события А,В,…,К образуют полную группу, то они единственно возможные и несовместные.

Т.к. события А,В,…,К – единственно возможные, то событие А + В + … +К, состоящее в появлении в результате испытания хотя бы одного из этих событий, является достоверным, то его вероятность = 1:

Р(А + В + … + К) = 1.

Т.к. события А,В,…,К – несовместные, к ним применима теорема сложения:

Р(А + В + … + К) = Р(А) + Р(В) + … + Р(К) = 1.

Следствие 2. Сумма вероятностей противоположных событий = 1:

4. 
   Полная группа событий. Противоположные события. Соотношения между вероятностями противоположных событий (с выводом). Пример.
   

Несколько событий образуют полную группу событий если в результате опыта обязательно появится хотя бы одно из них. Это означает, что в рез испытания должно произойти 1 и только 1 из этих событий.

Частным случаем событий , образующих полную группу, явл противоположные события. 2 несовместимых соб из кот-х 1 должно обяз-но произойти наз-ся противоположными. Событие противоположное соб А ->  . (появление герба и решки у монеты)

Доказательство теоремы о полной группе событий

Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то Р (A₁ + A₂ + ... + A_n) = 1.     (*)

Любые два события полной группы несовместны, поэтому можно применить теорему сложения: Р (А₁ + А₂ + ... + А_n) = Р (A₁) + Р (A₂) + ... + Р (А_n).    (**) 

Сравнивая (*) и (**), получим Р (А₁) + Р (А₂) + ... + Р (А_n) = 1.

Пример: Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В — 0,2. Найти вероятность того, что очередной пакет будет получен из города С.

Решение. События "пакет получен из города А", "пакет получен из города В", "пакет получен из города С" образуют полную группу, поэтому сумма вероятностей этих событий равна единице: 0,7 + 0,2 + p =1. Отсюда искомая вероятность р = 1 — 0,9 = 0,1.

Пример 2. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то противоположное событие — промах.

5. 
   Зависимые и независимые события. Произведение событий. Понятие условной вероятности. Теорема умножения вероятнос­тей (с доказательством).
   

События А,Б,В... называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий.

События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.

Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет, т.е.

Р_А(В) = Р(В) (или Р_А(В)=Р(В)).

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А - деталь годная, В - деталь окрашенная, то АВ - деталь годна и окрашена.

Произведением нескольких событийназывают событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С - появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС - выпадение «герба» во всех трех испытаниях.

Условной вероятностью (Р_A(В) - условная вероятность события В относительно А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Исходя из классического определения вероятности, формулу Р_A(В) = Р(АВ) / Р(А) где (Р(А)>0) можно доказать.

Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ) = Р(А) • Р_А(В) = Р(В) • Р_В(А).

Доказательство

З а м е ч ан и е. Применив формулу (*) к событию ВА, получим Р(ВА) = Р(В)•Р_В(А), или, поскольку событие ВА не отличается от события АВ, -> Р(АВ) = Р(В)•Рв(А).

Сравнивая формулы Р(АВ) = Р(А)•Р_A(В) и Р(АВ) = Р(В)•Рв(А), заключаем о справедливости равенства Р(А)•Р_А(В) = Р(В)•Рв(А).

Теорема (правило) умножения вероятностей легко обобщается на случай произвольного числа событий:

P(ABC...KL) = Р(А)· Р_А(В)· Р_АВ(С) ... Р_АВС...К(L),

Т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.

Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков - конусный, а второй - эллиптический.

Р е ш е н и е. Вероятность того, что первый валик окажется конусным (событие A), Р(А) = 3 / 10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик - конусный, т. е. условная вероятность Р_A(В) = 7 / 9. 

По теореме умножения, искомая вероятность Р(АВ) = Р(А)•Р_A(В) = (3/10)• (7/9) = 7/30. Заметим, что, сохранив обозначения, легко найдем: Р(В) = 7/10, Р_B(А) = 3/9, Р(В)•Р_B(А) = 7/30, что наглядно иллюстрирует справедливость равенства.

5. 
   ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ и БАЙЕСА (с доказательством). Примеры
   

Ф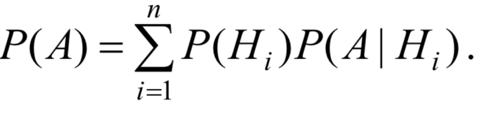
ормула полной вероятности. Пусть гипотезы (события) H1 , H2 ,..., Hn образуют полную группу несовместных событий. Нужно определить вероятность события А, которое может произойти вместе с одним из событий H1 , H2 ,..., Hn .

Поскольку гипотезы H1 , H2 ,..., Hn образуют полную группу несовместных n событий,то

П
ример. Есть 3 одинаковые урны. В первой находятся 2 белых и 1 черный шар, во второй – 3 белых и 1 черный, в третьей – 2 белых и 2 черных. Наугад выбираем одну урну и вынимаем из нее один шар. Найти вероятность того, что шар белый.

Р е ш е н и е . Пусть гипотезы H1 , H2 , H3 обозначают выбор первой, второй и третьей урны, событие А – появление белого шара. Так как гипотезы H1 ,H2,H3 равновероятны, то P(H1) = P(H2) = P(H3) =1/3. Условные вероятности P(A|H1)=2/3; P(A|H2)=3/4, P(A|H3)=1/2.