ргз физика. Решение(1). Краткие теоретические сведения

• Название: Краткие теоретические сведения
• Анкор: ргз физика
• Дата: 10.11.2021
• Размер: 203.5 Kb.
• Имя файла: Решение(1).doc
• Тип: Документы; #268782

Задание.

Тело массой брошено под углом к горизонту со скоростью м/с. Определить угол , под которым направлена скорость к горизонту и радиус кривизны траектории в момент времени , где − полное время полета. Построить графическую зависимость перемещения тела, от времени в процессе всего движения тела – , а также построить траекторию движения тела с указанием на ней положения тела в момент времени _.

Краткие теоретические сведения:

• 
  Система отсчета – это совокупность тела отсчета, системы координат и системы отсчета времени, связанных с этим телом, по отношению которого изучается движение(или равновесия) каких-либо других материальных точек или тел.
  
• 
  Координаты – это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве.
  
• 
  Материальная точка – это тело, размерами, которых можно пренебречь по сравнению с расстоянием до других тел.
  
• 
  Траектория – линия, которую описывает материальная точка при своем движении. Длина траектории называется пройденным частицей путем.
  
• 
  Перемещение – вектор , проведенный из начального положения частицы в конечное.
  
• 
  Скорость – производная перемещения по времени .
  
• 
  Ускорение – производная скорости по времени .
  
• 
  Кинематическое уравнение для скорости материальной точки, движущейся прямолинейно равномерно :
  

; ; .

• 
  Кинематические уравнения для скорости и перемещения материальной точки, движущейся прямолинейно равноускоренно :
  

; ; .

Решение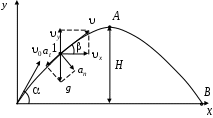

1. Для того что бы определить момент времени , определит общее время полета тела . Это время равно: , где – время полета до наивысшей точки траектории . Запишем кинематические уравнения для скорости тело в т. А.

; ; ;

; .

.

2. Угол найдем из треугольника скоростей:

.

Найдем проекции скорости на оси в точке 1.

м/с;

м/с;

.

3. Найдем радиус кривизны траектории. Из рисунка видно соотношение между скоростями и ускорениями:

; .

Горизонтальная проекция скорости , поскольку в горизонтальном направлении ускорения нет. Полная скорость: .

.

м/с.

Тогда радиус кривизны будет равен:

м.

4. Найдем зависимость .

;

; ;

;



Построим график зависимости потенциальной энергии тела от времени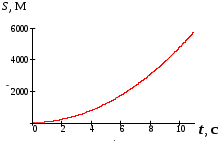

5. Найдем уравнение траектории движения тела .

;

; ;

;

.

Построим траекторию в координатах .

Вывод

В этой работе мы исследовали движение тела, брошенного под углом к горизонту; рассчитали требуемые значения:

• 
  угол ;
  
• 
  радиус кривизны м.
  

увидели, что графиком траектории движения является парабола: , отражающая криволинейное движение тела; показали график зависимости перемещения тела, от времени: .