Задачи о назначениях. Курсовая работа Целочисленное программирование. Задача о назначениях
 Скачать 0.59 Mb.
|
|
Государственное образовательное учреждение высшего профессионального образования Санкт-Петербургский Государственный Технологический институт (Технический университет) Кафедра Экономики и логистики Факультет Наукоемких технологий Учебная дисциплина Математика КУРСОВАЯ РАБОТА «Целочисленное программирование. Задача о назначениях» Студентка Савинова Д.И. Руководитель Межевич К.Г. Санкт-Петербург 2010г. Введение Целочисленное программирование - один из наиболее молодых, перспективных и быстро развивающихся разделов математического программирования. Можно перечислить большое количество разнообразных задач планирования экономики, организации производства, исследования конфликтных ситуаций, синтеза схем автоматического регулирования, которые формально сводятся к выбору лучших, в некотором смысле, значений параметров из определенной дискретной совокупности заданных величин. К ним можно отнести и экстремальные комбинаторные задачи, возникающие в различных разделах дискретной математики. Задачи и методы, относящиеся к перечисленному кругу вопросов, в литературе именуются по-разному. Наибольшее распространение получил термин «целочисленное программирование», однако встречаются и такие как «дискретное программирование», реже «комбинаторное (или диофантово) программирование». Наиболее изученными задачами этого класса являются целочисленные задачи линейного программирования, в которых на все переменные (или на их часть) наложено дополнительное требование целочисленности. От них принято отличать так называемые дискретные задачи линейного программирования, в которых область допустимого изменения каждой переменной - не множество целых неотрицательных чисел, а некоторое заданное конечное множество. Целочисленные задачи математического программирования могут возникать различными путями. . Существуют задачи линейного программирования, которые формально к целочисленным не относятся, но при соответствующих исходных данных всегда обладают целочисленным планом. Примеры таких задач - транспортная задача и ее модификации (задачи о назначениях, о потоках в сетях). . Толчком к изучению целочисленных задач в собственном смысле слова явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины. Они были названы задачами с неделимостью. Таковы, например, задачи об оптимизации комплекса средств доставки грузов, о нахождении минимального порожнего пробега автомобилей при выполнении заданного плана перевозок, об определении оптимального машинного парка и его оптимального распределения по указанным работам при условии минимизации суммарной стоимости (машинного парка и производимых работ), о нахождении минимального количества судов для осуществления данного графика перевозок и т. п. . Другим важным толчком к построению теории целочисленного программирования стал новый подход к некоторым экстремальным комбинаторным задачам. В них требуется найти экстремум целочисленной линейной функции, заданной на конечном множестве элементов. Такие задачи принято называть задачами с альтернативными переменными. В качестве примеров можно назвать задачи коммивояжера (бродячего торговца), об оптимальном назначении, теории расписания, или календарного планирования, и задачи с дополнительными логическими условиями (например, типа «или - или», «если - то» и т. п.). Исторически первой задачей целочисленного типа является опубликованная в 1932 г. венгерским математиком Е. Эгервари задача о назначении персонала. В 1955 г. на Втором симпозиуме по линейному программированию была рассмотрена задача о бомбардировщике, известная как задача о ранце. Цель данной работы: В данной работе я рассмотрю Целочисленное линейное программирование(ЦЛП) ориентированное на решение задач линейного программирования, также рассмотрю задачу о назначениях. На их примере решу задачи из этой области. 1. Целочисленное линейное программирование Целочисленное линейное программирование (ЦЛП) ориентировано на решение задач линейного программирования, в которых все или некоторые переменные должны принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На сегодня не существует надежных вычислительных алгоритмов решения таких задач. . Постановка транспортной задачи по критерию стоимости в матричной форме Транспортная задача (ТЗ) формулируется следующим образом. В m пунктах отправления A1,….,Am сосредоточен однородный груз в количествах соответственно a1,….,am единиц. Имеющийся груз необходимо доставить потребителям B1,….,Bn спрос которых выражается величинами b1,….,bn единиц. Известна стоимость сij перевозки единицы груза из i-го  пункта отправления в j-й  который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются.Для построения экономико-математической модели ТЗ рассмотрим матрицу 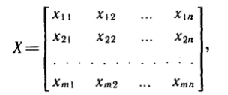 где  обозначает количество единиц груза, которое необходимо доставить из i-го пункта отправления в j-й пункт назначения.Матрицу Х=[хij]т×п будем называть матрицей перевозок. Предполагается, что все xij≥0. Удельные транспортные издержки (расходы) запишем в форме матрицы C = [cij]m×n и назовем ее матрицей тарифов. Для наглядности условия ТЗ можно представить таблицей (табл. 2.1), которую будем называть распределительной. Распределительную таблицу называют иногда табличной или матричной моделью ТЗ. Таблица 2.1  Экономико-математическая модель ТЗ должна отражать все условия и цель задачи в математической форме. Так, переменные  должны удовлетворять ограничениям по запасам, потребностям и условиям неотрицательности.В математической форме эти условия можно записать так. целочисленный отсечение транспортный гомори 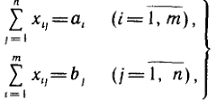 (2.1) (2.2)Цель ТЗ - минимизировать общие затраты на реализацию плана перевозок, которые можно представить функцией 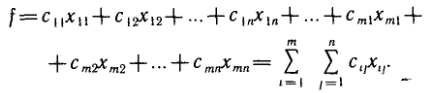 (2.3)Итак, математически ТЗ ставится так. Даны система ограничений (2.1) при условии (2.2) и линейная функция (2.3). Требуется среди множества решений системы (2.1) найти такое неотрицательное решение, при котором линейная функция (2.3) принимает минимальное значение (минимизируется). Будем называть план перевозок Х=[хij]т×п допустимым, если он удовлетворяет ограничениям (2.1) и (2.2). Допустимый план перевозок, доставляющий минимум целевой функции (2.3), называется оптимальным. . Задача о назначении (проблема выбора, задача о женихах и невестах) Она является исторически первой задачей дискретного программирования (опубликована венгерским математиком Е. Эгервари в 1932 г. как задача транспортного типа). Имеется n исполнителей, которые могут выполнять n различных работ. Известна полезность cij связанная с выполнением i-м исполнителем j-й работы.  Необходимо так назначить исполнителей на работы, чтобы добиться максимальной полезности при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должен быть закреплен только один исполнитель. Для составления математической модели задачи обозначим через xij факт назначения или неназначения i-го исполнителя на j-ю работу. Так как количество исполнителей равно количеству работ и каждый из них может быть назначен только на одну работу, то xij должны принимать только два значения: 1 или 0. Такие переменные называют булевыми. Итак, 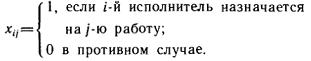 Приходим к задаче: найти план назначения xij, который максимизирует суммарную полезность назначений: 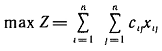 при следующих ограничениях. Каждый исполнитель назначается только на одну работу:  (3.1)На каждую работу назначается только один исполнитель  (3.2)Условия неотрицательности и целочисленности (булевости):  (3.3)Легко видеть, что задача о назначении - частный случай транспортной задачи при  Однако с учетом специфики задачи для ее решения разработаны специальные, более эффективные алгоритмы.Задача о назначении имеет самое широкое применение. Например, при закреплении машин за маршрутами, распределении инструментов для обработки различных марок стали, рабочих или бригад и т. д. В каждом конкретном случае математическая модель задачи может иметь специфику. Например, в задаче распределения алгоритмов между вычислительными машинами на ВЦ число распределяемых алгоритмов, как правило, не равно числу машин. При назначении на должности для некоторых исполнителей существуют ограничения. Прежде всего необходимо отметить, что если задача о назначениях ставится при условии получения максимального эффекта, то ее сводят к задаче на минимум. Пусть дана матрица эффективности C=[cij].В каждом столбце найдем максимальный элемент  Постро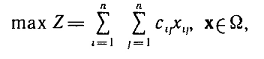им матрицу С'=[ lj-cij ]Задача  где 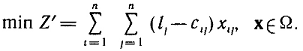 - область допустимых решений системы (3.1) - (3.3), эквивалентна задаче В самом деле, 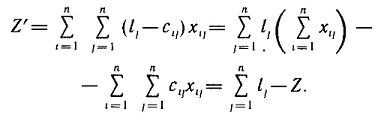 Функция Z' достигает минимума при условии, что Z достигает максимума,  Если в задаче о назначениях число исполнителей равно числу работ, то говорят о закрытой модели, в противном случае - об открытой модели задачи о назначениях. Если число m меньше числа исполнителей n (m И еще одна деталь. Если по каким-либо причинам запрещается выполнение какой-либо работы каким-либо исполнителем, то и в этом случае соответствующую клетку «блокируют бесконечностью» (ставят большую стоимость М). Точное решение задачи о назначениях можно найти венгерским методом, методом динамического программирования и др. Существует также много приближенных методов. Хорошее приближение дает модификация способа Фогеля для определения опорного плана транспортной задачи. Пример . При закреплении транспортных средств за маршрутами определена матрица прибылей 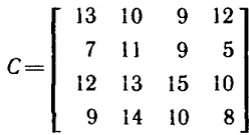 Найти план закрепления, максимизирующий суммарный эффект. Решение. Прежде всего сведем задачу на максимум к задаче на минимум. Для этого в каждом столбце матрицы С найдем максимальный элемент и вычтем из него элемент соответствующего столбца. Получим матрицу Сj задачи о назначениях: 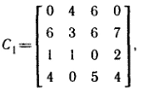 которую будем решать на минимум:  Для получения приближенного решения воспользуемся способом Фогеля для нахождения начального опорного плана транспортной задачи. В каждом ряду матрицы Сi найдем минимальный и ближайший к нему элементы и их разность по абсолютной величине записываем в конце соответствующего ряда справа и снизу (табл.3.1). Находим максимальную из этих разностей (число 5 заключено в рамку). В ряду, соответствующем максимальной разности, находим минимальный элемент  .Мысленно вычеркиваем из матрицы (табл. 3.1) строку и столбец, соответствующие этому элементу. Фиксируем полученное назначение. Для нашего примера закрепляем третье транспортное средство за третьим маршрутом, это закрепление в табл. 3.1 подчеркнуто. С оставшейся матрицей поступаем аналогично предыдущему. Все вычисления сведены в табл.3.1.Таблица 3.1 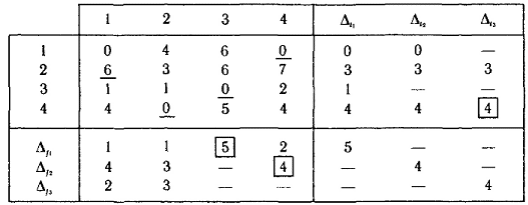 План назначения (1-4), (2-1), (3-3), (4-2), maxZ =с14+с21+с33+с42 =12 + 7+ 15+14 = 48. . Метод отсечения Алгоритм метода Гомори для решения полностью целочисленной задачи линейного программирования. Рассмотрим полностью целочисленную задачу линейного программирования 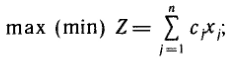 (4.1) (4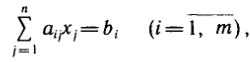.2) (4.3) (4.4)Алгоритм Гамори состоит из нескольких этапов: 1. Решается задача (4.1) - (4.3) с отброшенным условием целочисленности. 2. Полученное оптимальное решение (если оно существует) проверяется на целочисленность. Если условие целочисленности выполняется по всем переменным, то оптимальное решение задачи (4.1) - (4.4) совпадает с оптимальным решением задачи (4.1) - (4.3). Если это решение не выполняется хотя бы по одной переменной, то переходят к третьему этапу. Если задача (4.1)-(4.3) оказывается неразрешимой, то задача (4.1)-(4.4) тоже не имеет решения. 3. Строится дополнительное ограничение, отсекающее часть области, в которой содержится оптимальное решение задачи (4.1) - (4.3) и не содержится ни одного допустимого решения задачи (4.1) - (4.4). . Последний этап предусматривает возвращение к ЗЛП с отброшенным условием целочисленности, но с расширенной системой ограничений, в которую включено дополнительное ограничение, полученное на третьем шаге. К расширенной системе ограничений вновь применяется симплексная процедура. Если найденное таким образом решение будет опять нецелым, то формируется новое дополнительное ограничение и процесс вычислений повторяется. Алгоритм Гомори позволяет за конечное число шагов прийти к оптимальному целочисленному решению, если оно существует. С геометрической точки зрения каждому дополнительному линейному ограничению в n-мерном пространстве соответствует определенная гиперплоскость, отсекающая от многогранника решений некоторую его часть, включая и оптимальную на данном этапе нецелочисленную вершину. При этом все точки с целочисленными координатами, в том числе и искомая оптимальная, остаются в усеченном многограннике. Так как множество целых точек усеченного многогранника совпадает с множеством целых точек исходного многогранника, то понятно, что если оптимальное решение ЗЛП на усеченном многограннике удовлетворяет условию целочисленности, то оно является оптимальным целочисленным решением и исходной задачи. Через несколько операций отсечения искомая целочисленная точка оказывается сначала на границе, а затем становится оптимальной вершиной неоднократно усеченного многогранника решений. Может оказаться, что многогранник решений не содержит ни одной целочисленной точки. В этом случае, сколько бы ни вводили дополнительных ограничений, целочисленного допустимого решения получить нельзя. Для лучшего понимания существа вопроса обратимся к наглядной иллюстрации случая п=2 (рис. 4.1). Ограничения задачи определяют на плоскости x1Ox2 некоторый многоугольник М, в вершине  которого, если не учитывать условия целочисленности, достигается максимум целевой функции. Внутри этого многоугольника имеется конечное множество точек, которым соответствуют решения с целочисленными значениями переменных (на рисунке они обозначены кружочками). На рисунке показаны три прямые l1 ,l2 ,l3 соответствующие трем дополнительным линейным ограничениям. Каждая из прямых отсекает часть области допустимых решений. Так, после отсечения части области прямой оптимальной оказывается вершина  ,и, наконец, оптимальной становится целочисленная вершина  .Основное в алгоритме - составление дополнительного ограничения, т. е. отсекающей гиперплоскости, которая называется правильным отсечением. Правильное отсечение должно удовлетворять следующим условиям: 1) быть линейным; 2) отсекать найденное оптимальное нецелочисленное решение задачи (4.1) - (4.3); 3) не отсекать ни одной из целочисленных точек задачи (4.1) - (4.5).Рисунок 4.1 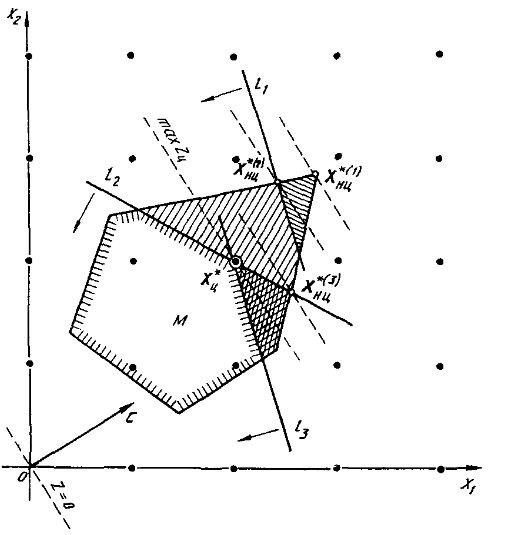 Формирование правильного отсечения. После каждой итерации система ограничений имеет вид 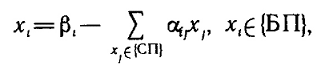 (4.5)где {БП} - множество базисных переменных. Если выполняется условие оптимальности задачи, то находим оптимальное решение. Если, все компоненты оптимального плана целочисленны, то задача решена. Предположим, что некоторые (  - нецелые. Пусть компонента i0 - нецелая. Рассмотрим i0 равенство системы (4.5), для которой выполняется условие оптимальности, т.е. (4.6)Напомним, что наибольшая целая часть числа а, его не превосходящая, обозначается [а], а дробная положительная- {а}. Причем  (4.7)Например, пусть а = 3,2. Имеем [3,2] = 3; {3,2}=0,2; 3,2 =3+0,2. Пусть а= - 4,3. Имеем [-4,3]=-5, {-4,3}=0,7, -4,3=-5 + 0,7. Перейдем к дальнейшему изучению уравнения (4.6). Найдем целую и дробную части его коэффициентов 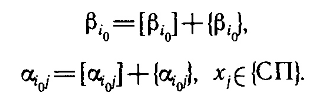 и  .Согласно равенству (4.7), имеем: (4.8)Так как, по предположению, нецелое, то  Кроме того,  . Подставив выражение (4.8) в равенство (4.6), получим (4.9)Так как первое слагаемое равенства (4.9) есть целое число, то, для того чтобы 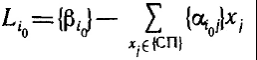 было целым, необходимо, чтобы второе слагаемое также было целым, т. е. величина должна быть целым числом. Так как xio- координата допустимого целочисленного решения задачи (4.1) - (4.4), то Li0 -всегда целое число. Покажем, что Li0≤0. В самом деле, величина 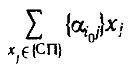 не может быть отрицательной. Из условия (4.7) следует  Так как Li0 -целое, то из предположения,что Li0 > 0, должно следовать  , что противоречит определению дробной части числа.Итак, доказано, что любое допустимое решение задачи (4.1) - (4.4) должно удовлетворять неравенству  (4.10)Решение задач Задача № 1 x1, x2, … , x5 - план погрузки (ед.) |xi ≥ 0 , xi Є Z |5x1 + 8x2 + 3x3 + 2x4 + 7x5 ≤ 112 |x1 + 8x2 + 6x3 + 5x4 + 4x5 ≤ 109 x1 + 7x2 + 6x3 + 5x4 + 4x5 → max. Опорный план: y1 = 112 y2 = 109 x1 = x2 = … = x5 = 0 целевая функция F = 4x1 + 7x2 + 6x3 + 5x4 + 4x5
Оптимальный нецелочисленный план x1 = ≈ 14,87 ; x4 = 433/23 ≈ 18,826 F = 3533/23 ≈ 153,606 Метод отсечения: Строим отсечение по строке x1 : {342/23} - {24/23} x2 - {3/23}x3 - {27/23} x5 - {5/23} y1 - {-2/23} y2 ≤ 0 - x2 - 3x3 - 4x5 - 5y1 - 21y2 ≤ 0 - Новое ограничение (отсечение) вынесем в симплекс таблицу
Строим отсечение по строе y2: {20/21} - {1/21}x2 - {1/7}x3 - {4/21}x5 - {5/21}y1 - {-1/21 }y3 ≤ 0 - x2 - 3x3 - 4x5 - 5y1 - 20y3 ≤ 0 - Новое ограничение (отсечение) внесем в симплекс таблицу:
Все идет к тому, что x1 = 15 ; x4 = 18 ; F = 150 Ответ: x1 = 15 ; x4 = 18 ; F = 150 Задача №2 Эксцентричный шейх оставил завещание относительно распределения стада верблюдов между тремя детьми: Тарик получает не менее половины стада, Шариф - не менее одной трети, а Майса - по меньшей мере, одну девятую часть. Остаток завещался благотворительной организации. В завещании не упоминался размер стада, говорилось лишь, что количество верблюдов - число нечетное и благотворительная организация получает в точности одного верблюда. Сколько верблюдов оставил шейх и сколько получил каждый из его детей? N - размер стада x - «Т» ; y - «Ш» ; z - «М» |N = 2n + 1 |x +y + z = 2n |x ≥ = N/2 = (2n +1)/2 =n+1/2 => x ≥ n+1 (x Є Z) |y ≥ N/2 |z ≥ N/9 N → min. 1) нашли нижнюю оценку целевой функции. ) нашли план, при котором она достигается => план оптимален x + 9y + 9z = 18n x + 9y + 9z ≥ 9(n + 1) + 3N + N = 9n + 9 + 4N = 9n + 9 + 4(2n + 1) = 17n + 13 n ≥ 17n +13 n ≥ 13 N ≥ 27 N = 27 ; x = 14 ; y = 9 ; z = 3. Ответ: размер стада=27 ,Тарик получил 14 верблюдов ,Шариф получил 9 верблюдов ,Майса получил3 верблюда. Задача №3 Супружеская пара фермеров посылает трех своих сыновей на базар продать 90 яблок, чтобы обучить их числам и обращению с деньгами. Самый старший Джим получил для продажи 50 яблок, Билл(средний) - 30 и самый младший Джон - лишь 10. Родители поставили пять условий. 1) Цена яблок должна быть равно либо 1 долл. за 7 яблок , либо 3 долл. за 1 яблоко. 2) Каждый ребенок может использовать один или оба варианта цен. 3) Все дети должны вернутся с одинаковой суммой денег. 4) Каждый ребенок приносит домой сумму, которая является четным числом (без центов). 5) Сумма денег, полученная каждым из детей, должна быть максимальной при сформулированных условиях. Считается, что дети могут продать все яблоки, которые они имеют. Как дети могут выполнить требования своих родителей?
ai, bi, ci Є Z ≥0 a1 + a2 = 50 b1 + b2 = 30 c1 + c2 = 10+ 3a2 = b1 +3b2 = c1 + 3c2 - выручка1 + 3a2 | b1 +3b2 | - четное ← пассивное условие c1 + 3c2 | = 7a1 + a2 = a1 + 3a2 + 6a1 - 2a2 Четное Четное + 3a2 = b1 +3b2 = c1 + 3c2 → max.+ 3c2 ≤ 301 = 0 , c2 = 10 b1 = 3 , b2 = 9 a1 = 6 , a2 = 8 Ответ: Джим продал 6 яблок по 1$ и 8 яблок по 3$ Билл продал 3 яблока по 1$ и 9 яблок по 3$ Джон ни продал ни одного яблока по 1$,но продал 10 яблок по 3$. Задача № 4 Капитан торгового судна, который хотел наградить трех членов команды за их героические усилия по спасению груза корабля во время неожиданного шторма, взял некоторую сумму денег у казначея и отдал приказ старшему помощнику распределить их поровну между тремя матросами после того, как корабль достигнет берега. Однажды ночью один уз матросов решил взять свою (справедливую) третью часть заранее. После деления денег на три равные части осталась одна монета, которую матрос решил оставить себе (в дополнение к третьей части денег). На следующую ночь второй матрос решил осуществить такой же план и, повторил деление на 3 части оставшейся суммы, присвоил себе еще и монету, которая осталась после деления. На третью ночь третий матрос взял третью часть того, что осталось, и одну дополнительную монету, которая осталась после деления. Когда корабль достиг берега, старший помощник капитана разделил остаток денег поровну между тремя матросами и снова осталась одна монета. Старший помощник отложил эту монету в сторону и вручил матросам предназначенные им равные части. Сколько денег было в самом начале? (задача имеет бесконечно много целочисленных решений. Предположите для удобства, что следует определить минимальную сумму денег, которая удовлетворяет условиям задачи. Увеличивая затем полученное решение на 1, рассмотрите его как нижнюю границу и получите новое минимальное решение. Продолжая таким образом, можно наметить шаблон общего решения.) Условие: N = 3n + 1 1-ый n +1 |2n = 3m +1 2-ой m + 1 |2m = 3l + 1 3-ий l + 1 |2l = 3k + 1 k, l, m, n > 0 Є Z N → min. Решение: x + 3y = 1 Диофантово ур-е : xn + yn = zn n ≥ 3 y + 1 делится на 2 y+1 делится на2 y нечетное y = 2u +1 x = 3y +1 = 3(2u +1) + 1 = 6u +4= 3u + 2 |x = 3u + 2 u Є Z |y = 2u +1= 2u +1 n = 3u + 2 u + 2 = 3l +1 l - 4u = 1 4u + 1 делится на 3 => u + 1 делится на3 u = 3v + 2 l - 4( 3v - 1)= 1 l = - 3 +12v= - 1 +4v ( - 1 + 4v) = 3k + 1 +8v = 3k + 1 v = 3k + 3 = 3(k + 1)= 3w w = 3(k + 1)= 8w - 1 w = 1= 4v - 1 = 12w - 1= 2u + 1 = 2(3v - 1) + 1 = 6v - 1 = 18w - 1= 3u + 2 = 3(3v - 1) + 2 = 9v - 1 = 27w - 1 = 3n + 1 = 3(27w - 1) + 1= 81w - 2 N = 79 1. 79 - 27 =52 27 . 52 - 18 = 34 18 . 34 - 12 = 22 12 Выводы по работе В ходе курсовой работы я научилась решать задачи ЦЛП ,задачи о назначениях, решать методом отсечения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На сегодня не существует надежных вычислительных алгоритмов решения таких задач. Узнала, что: Метод назначений - это один из методов линейного программирования, который предназначен для оптимального подбора n "предложений" к n "потребностям", например, для назначения вида работы машине, назначения вида работы производственному отделу, назначения человека на должность и т.д. Метод назначений применяется при решении задач, имеющих следующие характеристики: . Имеется n "предметов", которые должны быть распределены по n "пунктам назначения". . Каждый "предмет" должен быть назначен единственному "пункту назначения". В понятие "предмет" и "пункт назначения" может вкладываться различное смысловое значение, определяемое конкретной задачей менеджмента. Так в качестве предмета может выступать определенный вид деятельности (работы), должность, человек и т.д. . Оптимальный подбор назначений должен быть достигнут за счет максимизации или минимизации определенной меры эффективности назначения: прибыли или стоимости. Для каждого потенциального назначения оценивается мера эффективности. Если мерой эффективности является прибыль, то в процессе решения задачи о назначениях она максимизируется, если мерой эффективности является стоимость, она минимизируется. Список используемой литературы 1. Аркин П.А., Межевич К.Г Исследование операций/учебное пособие.-СПб.: СПбГТИ(ТУ),2008.-333с. . А.В. Кузнецов, В.П. Сакович, И.И. Холод Высшая математика. Математическое программирование/Минск «ВЫШЕЙШАЯ ШКОЛА» 1994.-288с. . Х. Таха. Введение в исследование операций. Т.2. - М. : Мир, 1985. . В.Н. Серпинский О решении уравнений в целых числах. - М.: Физматлит, 1961. - 88 с. Приложение Диофа́нтово уравнение - это уравнение вида  где P - целочисленная функция (например, полино с целыми коэффициентами), а переменные x i принимают целые значения. Названы в честь древнегреческого математика Диофанта. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||