ММОС КуР Дискретная обработка сигналов и цифровая фильтра. Курсовая работа по дисциплине Методы математической обработки сигнала на тему
 Скачать 6.32 Mb.
|
|
Федеральное агентство по образованию Томский Государственный Университет Систем Управления и Радиоэлектроники (ТУСУР) Кафедра теоретических основ радиотехники (ТОР) Курсовая работа по дисциплине Методы математической обработки сигнала на тему: Дискретная обработка сигналов и цифровая фильтрация . ЗАДАНИЕ к курсовой работе по курсу «Радиотехнические цепи и сигналы» .Тема работы: Дискретная обработка сигналов и цифровая фильтрация. .Срок сдачи работы Исходные данные и литература: Спектральный анализ периодических и непериодических управляющих сигналов . Выполнить математическое описание заданного периодического сигнала, изобразить графически два-три периода сигнала, указав на рисунке параметры, характеризующие сигнал. . Проанализировать временные свойства сигнала, описать заданные виды симметрии (и построить четную и нечетную составляющие сигнала) и сформулировать обоснованные предположения о свойствах и особенностях спектрального состава сигнала. . Вычислить и построить спектры амплитуд и фаз (не менее десяти спектральных составляющих). Выявить характер огибающей спектра амплитуд. . Построить оценку сигнала из трех гармонических колебаний с наибольшими амплитудами. . Рассчитать относительную погрешность представления сигнала оценкой из трех гармонических колебаний. 6. Определить комплексную спектральную плотность непериодического сигнала, совпадающего с заданным периодическим на протяжении одного периода в симметричных пределах [  ] и равного нулю при других временах.. Построить графики модуля спектральной плотности и фазового спектра непериодического сигнала. . Сопоставить спектры периодического и непериодического сигнала на основе известного соотношения  .Ряд значений  совместить с графиком спектральной плотности.. Определить энергию и среднюю мощность заданного сигнала на участке цепи с сопротивлением 1 Ом. . Сделать выводы по проведенному анализу периодического и непериодического сигналов, сопоставив между собой характер спектров, временное и спектральное представления сигналов. Расчет похождения непериодического сигнала сложной формы через линейную цепь второго порядка . Рассчитать и построить в масштабе АЧХ и ФЧХ цепи (постоянную времени цепи полагать равной интервалу времени t1). . Рассчитать и построить в масштабе переходную и импульсную характеристики цепи. . Проверить выполнение предельных соотношений между частотными и временными характеристиками. . Дать поинтервальное аналитическое представление сигнала по его графику. . Рассчитать операторным методом отклик на выходе линейной цепи и дать его поинтервальное описание. . По результатам вычислений (не менее трех точек на каждом интервале описания сигнала) изобразить отклик цепи на отрезке времени от момента включения до tmax, в три раза превышающем длительность воздействия; сигнал воздействия и отклика совместить на одном рисунке. . Сделать выводы по искажению сигнала при прохождении по цепи (интерпретация полученных результатов). Дискретная обработка аналогового сигнала . Дискретизировать заданный сигнал и восстановить аналоговый сигнал, используя ряд Котельникова. При определении верхней частоты спектра сигнала использовать пороговый критерий (амплитуды спектральных составляющих при w > wв не превышают 10% от уровня максимального значения). .Рассчитать спектр дискретной последовательности, определенной в пункте 1. Построить график. . Найти Z-преобразование найденной в пункте 1 дискретной последовательности. . Графоаналитическим методом определить комплексный коэффициент  дискретного преобразования Фурье той же дискретной последовательности.. Определить дискретное преобразование Фурье (ДПФ) той же дискретной последовательности. Построить график комплексных коэффициентов  . Восстановить аналоговый сигнал, используя тригонометрический ряд Фурье.. По результатам пункта 5 найти исходную дискретную последовательность, применяя обратное дискретное преобразование Фурье к . Построить график.. Произвести сравнение результатов вычислений: ) сравнить форму спектра дискретизированной последовательности со спектром исходного аналогового сигнала; ) установить связь между: а) результатом Z-преобразования и спектральной плотностью дискретной последовательности; б) спектром исходного периодического аналогового сигнала и дискретными отсчетами его спектральной плотности. Цифровая фильтрация. Синтез ЦФ по известному аналоговому фильтру-прототипу . Для заданной аналоговой электрической цепи (таблица А.3) найти операторное выражение передаточной функции К(р) и импульсную характеристику g(t). . Осуществить синтез цифровой цепи методом билинейного Z-преобразования по найденной в пункте 1 К(р). Построить схему алгоритма цифрового фильтра (ЦФ). . Рассчитать и построить амплитудно-частотную (АЧХ), фазочастотную (ФЧХ) и импульсную характеристики ЦФ. . Произвести синтез ЦФ с помощью метода инвариантности импульсной характеристики по найденной в пункте 1 g(t). Построить схему алгоритма ЦФ. . Найти отклик одного из рекурсивных ЦФ в виде выходной дискретной последовательности на входную дискретную последовательность, полученную в первой части курсовой работы. . Сделать выводы о сравнении методов синтеза по трудоемкости, сложности конечного результата, о физической достоверности полученной формы отклика в реальных условиях прохождения дискретного сигнала через синтезированную цепь. Содержание 1. Введение . Первая часть .1 Дискретизация аналогового сигнала .2 Расчет спектральной плотности дискретизированного сигнала .3 Расчет коэффициентов Ск с помощью дискретного преобразования Фурье .4 Восстановление исходного сигнала по ДПФ .5 z-преобразование дискретной последовательности .6 Восстановление аналогового сигнала с использованием ряда Котельникова .7 Сравнение результатов вычислений. . Вторая часть . 1 Расчет передаточной функции цепи .2 Синтез ЦФ методом инвариантности импульсной характеристики .3 Синтез ЦФ методом билинейного z-преобразования .4 Расчет импульсной характеристики ЦФ .5 Прохождение дискретного сигнала через ЦФ Заключение Список использованной литературы сигнал цепь цифровой 1. Введение Одним из основных и перспективных направлений современной обработки радиосигналов является цифровая фильтрация. В её основе лежит преобразование сигналов в последовательности чисел и обработка этой последовательности в цифровом вычислительном устройстве, роль которого может выполнять как универсальная ЭВМ, так и специализированный цифровой процессор. Применение в радиоэлектронике цифровой фильтрации открывает дополнительные возможности при обработке сигналов. В частности, могут быть реализованы сложные алгоритмы фильтрации, которые аналоговыми методами в ряде случаев вообще не удаётся осуществить. С другой стороны, возможен синтез в цифровой форме аналогов известных радиотехнических устройств различного функционального назначения, а именно: фильтров, преобразователей частоты, детекторов и т.п. Дискретные сигналы используются тогда, когда источник (приёмник) сообщений выдает (принимает) информацию в фиксированные моменты времени. Простейшая математическая модель такого сигнала - это счетное множество точек на оси времени, в каждой из которых определено отсчетное значение какого-либо непрерывного сигнала. Точки на оси отстоят друг от друга на равный промежуток, называемый интервалом дискретизации. Очевидное преимущество дискретных сигналов - нет необходимости воспроизводить сигнал непрерывно во все моменты времени. Благодаря таким сигналам появилась возможность строить многоканальные системы связи, использующие разделение каналов по времени (цифровая телефонная, сотовая связь). Цифровые сигналы являются разновидностью дискретных. Для них отсчетные значения представлены в форме чисел. Для удобства реализации и обработки цифровых сигналов обычно используются двоичные числа с ограниченным числом разрядов. В наше время системы с цифровыми сигналами не заняли только те ниши радиотехники, где они в принципе неприменимы. Такой широкий охват обусловлен многообразием методов обработки цифровых сигналов и фактически неограниченной точностью и надежностью этой обработки. Данная курсовая работа ставит своей целью привить практические навыки в области дискретной и цифровой обработки сигналов на примере решения конкретной задачи, включающей в себя элементы как синтеза, так и анализа цифрового фильтра. Задание на курсовую работу состоит из двух частей. Первая часть включает подготовку аналогового сигнала к цифровой обработке. Вторая часть содержит синтез и анализ цифрового фильтра. 2. Основная часть Расчет шифра  ;N1N2 = 37. ;N3N4 = 22. ;N5N6 = 24. ;N7N8 = 18. ;N9N10 = 57..1 Дискретизация аналогового сигнала Исходный сигнал представлен на рисунке 2.1. Параметры сигнала: t1=Т;t2=1,5·t1; t3=2,5·t1; Tс=4t1.  Рис. 2.1 - Представление исходного сигнала. Для удобства значения Е и t1 примем равными единице. В дальнейшем в программе MathCAD можно будет изменить их на указанные значения в ТЗ. Схема аналогового фильтра приведена на рисунке 2.2. 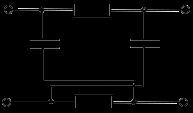  , Рис. 2.2 - Схема аналогового фильтра. Построим непериодический импульсный сигнал S(t): 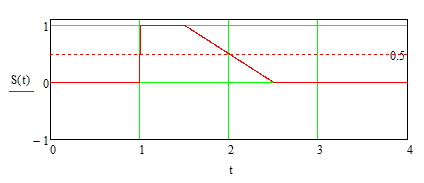 Рис. 2.3 - Исходный сигнал Поинтервальное описание сигнала выглядит следующим образом:  Воспользовавшись прямым преобразование Фурье (ППФ), получим 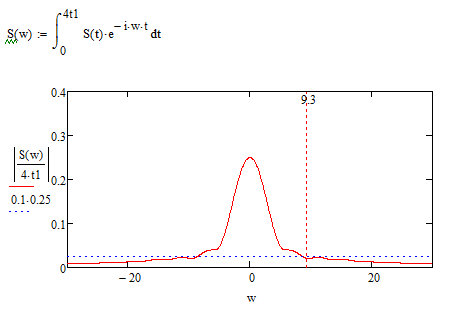 Рис. 2.4 - Амплитудно-частотная характеристика исходного сигнала 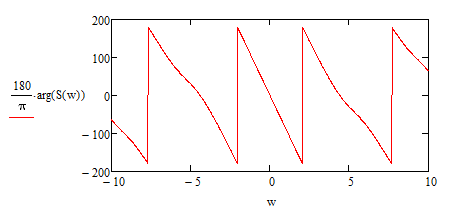 Рисунок 2.5 График аргумента комплексной спектральной плотности .2 Дискретизация аналогового сигнала по времени Руководствуясь теоремой Котельникова, частоту дискретизации  выбираем так, чтобы  . Для определения  спектра сигнала воспользуемся пороговым критерием: для частот выше модуль спектральной плотности не превышает уровня 0,1 от максимального значения. Графически определив  (рис. 2.2 ), получили: =9,3 рад/с, значит  =18,6 рад/с. Используем ее для определения периода дискретизации сигнала. =0,337 с.(2.3)Строго говоря, все реальные сигналы имеют конечную длительность и, следовательно, бесконечно протяжённый спектр. Однако, начиная с некоторого значения частоты, спектральные составляющие становятся настолько малы, что ими можно пренебречь. Сигнал может быть приближённо описан конечным числом выборочных значений. Число выборочных значений, которыми полностью описывается сигнал, называют числом степеней свободы сигнала. Число отсчетов (число степеней свободы) равно  .(2.4)Число отсчетов должно быть целым, поэтому, основываясь на выражение (2.4), принимаем:  Произведем пересчет параметров дискретизации в соответствии с принятым решением:  (2.5)Теперь сигнал можно приближенно представит в виде последовательности отсчетов. Запишем отсчеты дискретизированного сигнала и проиллюстрируем полученный результат (рисунок 2.6):  Изобразим полученную дискретную последовательность. 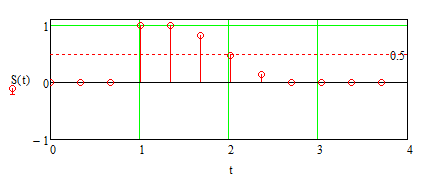 Рисунок 2.6 - Дискретная последовательность Спектральную плотность дискретного сигнала  можно вычислить непосредственно по отсчетам сигнала  , применяя прямое преобразование Фурье: (2.7)На рисунке 2.5 изображён модуль спектральной плотности дискретного непериодического сигнала 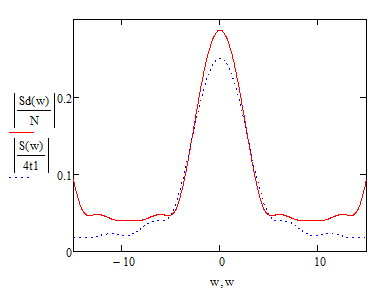 . Рисунок 2.7 Модули спектральных плотностей исходного аналогового (пунктирная линия) и дискретизированного (сплошная линия) сигналов. Анализируя рисунок 2.7 можно сделать очень важный вывод: при дискретизации сигнала во временной области спектральная плотность становится периодической функцией частоты с периодом, равным  . В то время как континуальный сигнал имеет апериодический спектр.Анализируя рисунок 2.7, можно сделать вывод: при дискретизации сигнала во временной области спектральная плотность этого сигнала становиться периодической функцией частоты с периодом, равным d. С помощью прямого дискретного преобразования Фурье (ПДПФ) установим связь между временными отсчетами сигнала и отсчетами его спектральной плотности:  (2.8)Результаты расчета значений коэффициентов ДПФ и график модуля коэффициентов Ск приведены на рисунке 2.8. 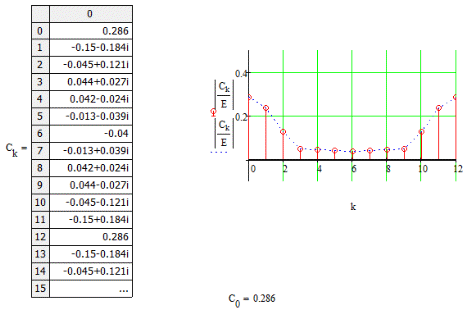 Рисунок 2.8 Отсчёты спектральной плотности, полученные по ДПФ Дискретный периодический сигнал обладает дискретным периодическим спектром. Отсчёты во временной и частотной областях связаны парой ДПФ. Дискретное преобразование Фурье сопоставляет отсчетам сигнала во временной области отсчеты спектральной плотности в частотной области. Ис пользуя частотные отсчеты, которые являются коэффициентами ДПФ, можно восстановить исходный аналоговый сигнал, применяя ряд Фуръе:  Учитывая четное количество коэффициентов ДПФ и их комплексную сопряженность, получаем  где 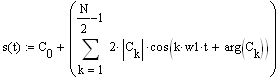 - фазовый угол коэффициента ДПФ. Следует отметить, что восстановление непрерывного сигнала по данной формуле есть не приближённая, а точная операция, полностью эквивалентная получению текущих значений сигнала с ограниченным спектром по его отсчётам. На рисунке 2.9 представлен результат восстановления сигнала по отсчётам его спектральной плотности. 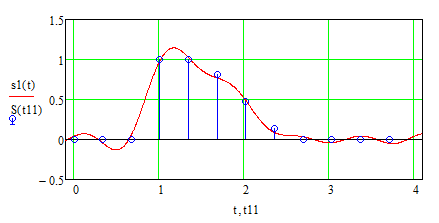 Рисунок 2.9 Аналоговый периодический сигнал, восстановленный по ДПФ Восстановленный сигнал является периодической функцией времени. Он точно проходит по отсчётам выборки на первом периоде. Очевидно, что при большем значении N восстановление будет точнее. Восстановление аналогового сигнала по заданным отсчётам произведем, используя ряд Котельникова, а именно:  Восстановленный сигнал представляет собой сумму функций Котельникова с весами, равными отсчётам сигнала. На рисунке 2.10 приведён результат восстановления. Рисунок 2.10 Аналоговый сигнал, восстановленный с помощью ряда Котельникова Как видно из рисунка, форма восстановленного сигнала приближенно напоминает форму исходного сигнала. Восстановленный сигнал сохранил апериодичность. Значения восстановленного сигнала совпадают со значениями исходного только в точках отсчета. Это объясняется тем, что нули функций Котельникова расположены по оси абсцисс (временной) с периодом, зависящим от аргумента функций. В нашем случае этот период равен  , то есть в каждой точке отсчета все сдвинутые относительно этой точки функции равны нулю, а функция, симметричная в этой точке, равна единице, что после домножение на значение отсчета дает точное совпадение с исходным сигналом. Во всех остальных точках функции Котельникова накладываются друг на друга, приближая форму итогового сигнала к исходному. Увеличение числа отсчетов повысит точность восстановления сигнала.По результатам работы проведённой в первом пункте можно сделать следующие выводы: Спектр дискретизированной последовательности получается путём суммирования бесконечного числа копий спектра исходного аналогового сигнала, сдвинутых относительно друг друга на частоту дискретизации.преобразование дискретной последовательности получается из спектральной плотности этой последовательности путём замены:  .Значения дискретных отсчётов спектральной плотности исходного аналогового сигнала совпадают со спектром периодического аналогового сигнала в точках n·с. 3. Вторая часть .1 Расчет передаточной функции цепи Для заданной аналоговой электрической цепи найти операторное выражение передаточной функции K(p) и импульсную характеристику g(t). Схема аналогового фильтра приведена на рисунке 3.1. , Рис. 3.1 - Схема аналогового фильтра. Схема представляет собой мост и для него мы имеем следующее:   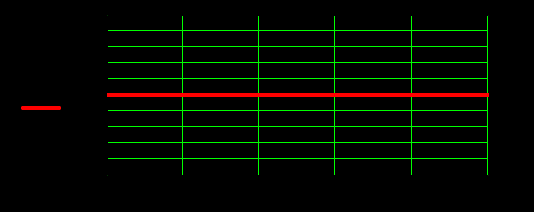  Модуль K(w) = 0 следовательно цепь не усиливает и не ослабляет сигнал, а просто передает входной сигнал на выход.  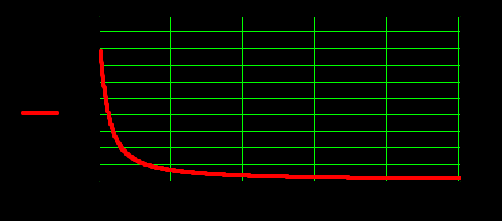 Рассчитаем и построим переходную и импульсную характеристики:  - переходная характеристика  Приравниваем знаменатель к нулю и найдем особые точки: = 0 k = 1= -b k = 1 Получили два полюса кратности единица. Берем вычеты в этих точках:   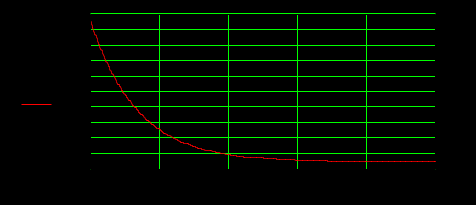    Опять воспользуемся математическим аппаратом вычетов:  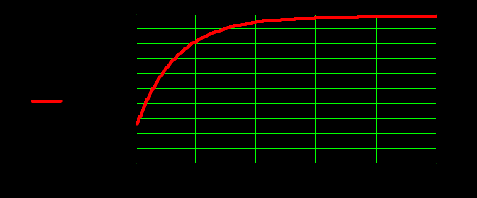     Все соотношения выполняются   3.2 Осуществить синтез цифровой цепи методом билинейного преобразования по найденной в пункте 3.1. K(p). Построить схему алгоритма цифрового фильтра. Данный метод позволяет с помощью билинейной замены установить однозначное непрерывное отображение из p - плоскости в z - плоскость. Эта связь имеет следующий вид: Используя билинейную замену, преобразуем передаточную функцию аналогового фильтра-прототипа следующим образом:  Определим  :  Упростим выражение с учетом дельта-функции:  Трансверсальная часть ЦФ описывается числителем, а рекурсивная знаменателем. Таблица 3.1 - коэффициенты  и  ЦФ.
Структурная схема ЦФ:  Работа рекурсивного БИХ-фильтра описывается алгоритмом:  .3 Рассчитать и построить амплитудно-частотную, фазо-частотную и импульсную характеристики ЦФ Чтобы от системной функции ЦФ перейти к его АЧХ, достаточно сделать замену:   На рисунке 3.3.1 приведена АЧХ ЦФ с параметрами: 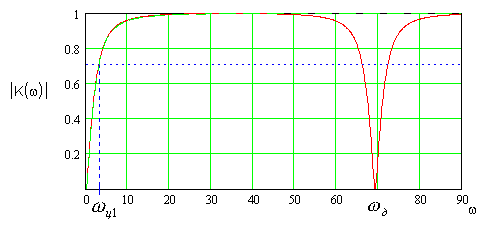 Рисунок 3.3.1 АЧХ цифрового фильтра 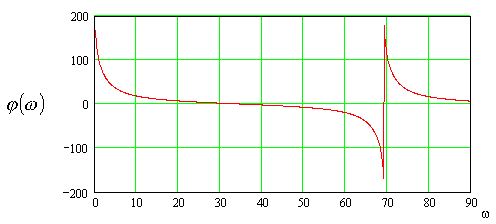 Рисунок 3.3.2 ФЧХ цифрового фильтра Для получения импульсной характеристики цифрового фильтра произведем обратное Z - преобразование системной функции ЦФ:     , при  Значение отсчета импульсной характеристики 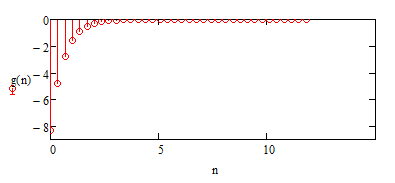 равно  . Рисунок 3.3.3 Отсчеты импульсной характеристики ЦФ .4 Произвести синтез ЦФ с помощью метода инвариантности импульсной характеристики по найденной в пункте 6.3.1. g(t). Построить схему алгоритма ЦФ. Продискретизируем импульсную характеристику аналогового фильтра-прототипа.Для дискретизации импульсной характеристики необходимо непрерывный аргумент t заменить на дискретный -  : где На рисунке представлена дискретизированная импульсная характеристика: Рисунок 3.4.1 Дискретизированная импульсная характеристика Системная функция трансверсального ЦФ представляет собой сумму вида: 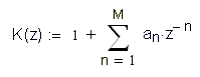 где  .Коэффициенты  приведены в таблице 3.4.1:
Начиная с n = 4 значения коэффициентов не превышают уровня 0.1 от максимального. Поэтому порядок M трансверсального фильтра равен 4. Структурная схема трансверсального фильтра приведена на рисунке 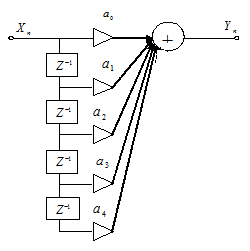 Рисунок 3.4.2 Структурная схема трансверсального фильтра Работа трансверсального ЦФ 8-го порядка описывается алгоритмом:  Сделав замену 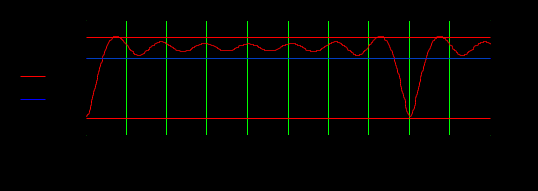 ,получим АЧХ трансверсального ЦФ восьмого порядка с параметрами: Рисунок 3.4.3 АЧХ трансверсального ЦФ Пульсации АЧХ трансверсального фильтра объясняются ограничением импульсной характеристики во времени. Цифровой фильтр с бесконечной импульсной характеристикой реализуется при учете в дискретной импульсной характеристике бесконечного числа слагаемых. При этом мы имеем бесконечно убывающую геометрическую прогрессию, сворачивая которую, получим системную функцию ЦФ канонического вида:   Коэффициенты и  рекурсивного ЦФ приведены в таблице 3.4.2:Таблица 3.4.2 - Коэффициенты и рекурсивного ЦФ
Структурная схема рекурсивного ЦФ приведена на рисунке 3.4.4: 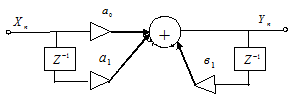 Рисунок 3.4.4 Структурная схема рекурсивного цифрового фильтра Работа рекурсивного БИХ - фильтра описывается алгоритмом:  Сделав замену 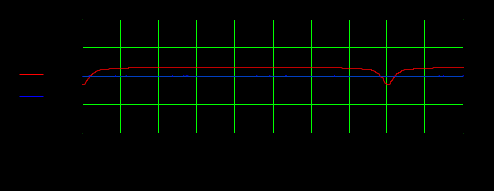,получим АЧХ рекурсивного ЦФ  Рисунок 3.4.5 АЧХ рекурсивного ЦФ Периодичность АЧХ ЦФ является результатом дискретизации импульсной характеристики аналогового фильтра-прототипа. АЧХ рекурсивного фильтра, полученного методом инвариантности импульсной характеристики, более точно повторяет частотную характеристику аналогового фильтра-прототипа, но при этом его необходимо проверять на устойчивость данный фильтр устойчив, т.к все коэффициенты попадают в круг единичного радиуса. .5 Найти отклики рекурсивных ЦФ на входную дискретную последовательность, полученную в первой части курсовой работы Дискретная свертка задается следующим выражением:  ,где  это значения отсчетов входного сигнала, которые были найдены в пункте 2.1. На рисунке 3.5.1 приведены отсчеты сигнала на выходе ЦФ полученного методом билинейной замены: 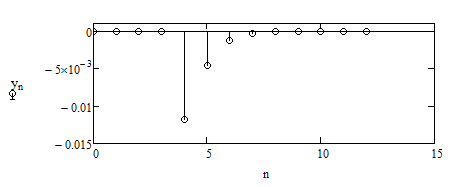 Рисунок 3.5.1 Результат прохождения сигнала через ЦФ, полученный методом билинейной замены Так как БИХ - фильтр имеет как трансверсальную, так и рекурсивную части, то отклик этого фильтра асимптотически стремится к нулю, имея бесконечную длительность. Заключение Синтез фильтров рассмотренных в данном разделе проводится на основе аналогового фильтра прототипа. В данном случае фильтром прототипом является последовательный резонансный контур с потерями. Принципиальным отличием цифровых фильтров от фильтра прототипа является то, что их АЧХ имеют периодический характер. Этот эффект появляется вследствие дискретизации. Наиболее просто рассчитываемый фильтр, это трансверсальный фильтр, который рассчитывается методом инвариантной импульсной характеристики. Однако в данном случае, для получения удовлетворительной АЧХ, приходится брать большое количество отсчётов. Это объясняется тем, что при синтезе трансверсального фильтра берётся конечное число отсчётов импульсной характеристики, а часть импульсной характеристики отбрасывается. Но так как импульсная характеристика контура затухает медленно, приходится брать большее количество отсчётов. Однако, трансверсальный фильтр однозначно устойчив, так как выходной сигнал зависит только от входной последовательности. Рекурсивный фильтр имеет меньше элементов, так как он использует не только входную, но и выходную последовательность. Он более точно повторяет АЧХ аналогового фильтра прототипа, но рекурсивный фильтр необходимо проверять на устойчивость. Фильтр, полученный на основе билинейного Z-преобразования, не допускает наложения АЧХ. Это достигается с помощью билинейной замены. Таким образом АЧХ аналогового фильтра прототипа как бы сжимается из бесконечности до ωв. Причём на низких частотах АЧХ ЦФ практически повторяет АЧХ фильтра прототипа и чем ближе к ωв ,тем больше искажения в АЧХ. В данном случае это сильно сказывается на импульсной характеристики ЦФ. Так как происходит сжатие частот, резонансная частота смещается и импульсная характеристика ЦФ будет иметь другую частоту, чем импульсная характеристика аналогового фильтра прототипа Список рекомендованной литературы 1. Радиотехнические цепи и сигналы. Дискретная обработка сигналов и цифровая фильтрация. Методические указания по выполнению курсовой работы Каратаева Нина Александровна Методические указания Томск: ТМЦДО, 2014. - 70 с. . Радиотехнические цепи и сигналы. Дискретная обработка сигналов и цифровая фильтрация Каратаева Нина Александровна Учебное пособие Томск: ТМЦДО, 2008. - 263 с. |
