Лабы подземка. Лабы-подземка. Лабораторная работа 1 исследование прямолинейнопаралельного установившегося фильтрационного потока несжимаемой
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Лабораторная работа №1 ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНО-ПАРАЛЕЛЬНОГО УСТАНОВИВШЕГОСЯ ФИЛЬТРАЦИОННОГО ПОТОКА НЕСЖИМАЕМОЙ ЖИДКОСТИ В ОДНОРОДНОМ ПЛАСТЕ 1.1. Краткая теория вопроса Прямолинейно-параллельным установившимся фильтрационным потоком считается такой поток, в котором траектории движения частиц жидкости совпадают с линиями токов, траектории параллельны, а скорости фильтрации во всех токах любого поперечного сечения (перпендикуляр-ного линиям токов) равны друг другу. Законы движения вдоль всех траектории такого фильтрационного потока одинаковы и потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат - ось X (рис.1.1). Такой поток называется одномерным. 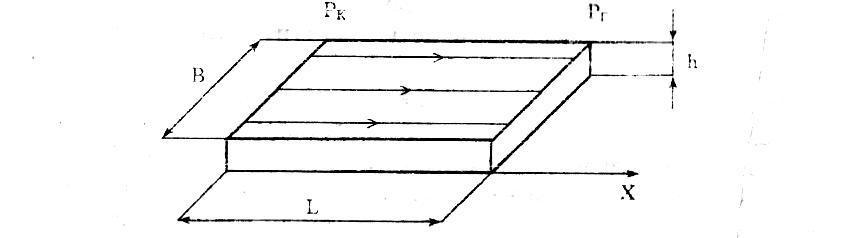 Рис.1.1. Схема прямолинейно-параллельного фильтрационного потока в пласте В лабораторных условиях прямолинейно параллельный одномерный поток имеет место при движении жидкости или газа через цилиндрический керн или через трубку постоянного диаметра, заполненную пористой средой. Пласт, в котором имеет место прямолинейно-параллельный поток, можно схематизировать в виде прямоугольного параллелепипеда длиной lk, шириной В и высотой h (толщина пласта) - рис.1.1. Левая грань является контуром питания - здесь давление постоянное, равно Рк, правая грань является поверхностью стока (галерея) с давлением Pp. Все остальные грани непроницаемы. Подобная картина может наблюдаться на отдельных участках пластов залежей нефти и газа при движении жидкости от нагнетательных скважин к эксплуатационным. Такие пласты часто называются полосообразными. Исследование задач одномерного потока относится к классу краевых задач математической физики. Так, дифференциальное уравнение одномерной прямолинейно-параллельной установившейся фильтрации несжимаемой жидкости по закону Дарси и в однородной пористой среде имеет вид d2P / dx = 0, (1.1) Интегрируя уравнение (1.1) при граничных условиях и параметрах пласта и флюида, получают закон распределения давления при установившейся фильтрации жидкости в полособразном пласте : где Р(х) - давление в произвольной точке X пласта. Па (1 Па = 1 Н/м): Рк и Pг- заданное давление на контуре питания и галерее соответственно, Па; LK - длина пласта, м: х - координата точки пласта, отсчитываемая от контура питания, м. Уравнение (1.2) показывает, что теоретическое распределение давления в пласте при установившейся фильтрации несжимаемой жидкости графически представляется в виде прямолинейного графика. Эта прямая называется пьезометрической линией. Градиент давления (в Па/м) в этом случае определяется выражением gradP = d2P / dx= Скорость фильтрации (в м/с) согласно закону Дарси равна: где k - коэффициент проницаемости пласта, м2; μ - коэффициент динамической вязкости жидкости, Па*с; (μ20 воды = 1 Мпа*с). Дебит галереи (объемный расход жидкости в м3/с) равен где F = Bh - площадь поперечного сечения пласта, м2- площадь фильтрации; В - ширина пласта, м; h - толщина пласта, м; ΔР = Рк- Рг — депрессия на пласт, равная разности давлений на контуре питания и галерее, Па; Закон движения жидких частиц определяется как 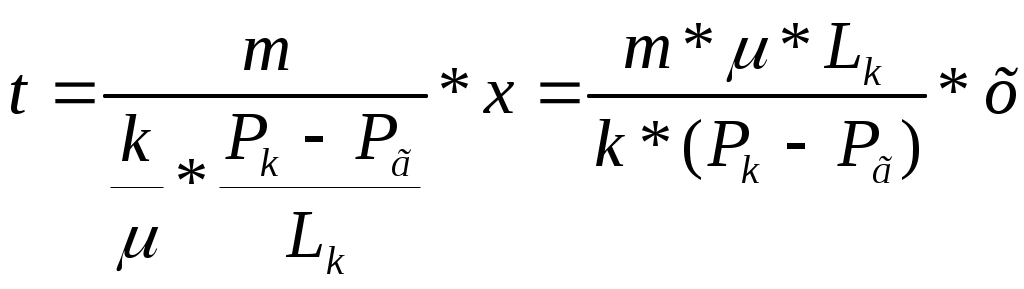 (1.6) (1.6)Средневзвешенное по объему порового пространства пластовое давление определяется как среднее арифметическое между давлением на контуре питания и на галерее: Т.к. площадь фильтрации полосообразного пласта величина постоянная, то при установлении фильтрации несжимаемой жидкости расход жидкости одинаков через любое поперечное сечение пласта и скорость фильтрации также величина постоянная, не зависящая от координаты. Скорость фильтрации связана с действительной средней скоростью движения жидкости W соотношением, м/с: V=m * W , (1.8) где m - коэффициент пористости пласта; W - действительная средняя скорость движения жидкости, м/с. Из (1.8) видно, что при прямолинейно-параллельной фильтрации несжимаемой жидкости скорость движения также не зависит от координаты. Скорость фильтрации, скорость движения и дебит галереи зависят от депрессии на пласт. Эта зависимость имеет линейный характер только при выполнении линейного закона фильтрации Дарси, когда потери давления при движении флюидов в пористой среде с небольшими скоростями обусловлены проявлениями сил вязкости (сил трения). Линейный закон фильтрации Дарси применим только в определенном диапазоне режимов фильтрации, т.е. необходимо выделить верхнюю и нижнюю границы применимости закона Дарси и соответствующие им дне группы причин. Верхняя граница применимости закона Дарси характеризуется некоторой верхнекритической скоростью фильтрации Vвкр. При высоких скоростях фильтрации выше ивкр закон Дарси нарушается из-за проявления сил инерции. Нижняя граница характеризуется проявлением неньютоновских реологических свойств пластовых флюидов, их взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации, меньших некоторой нижнекритической скорости фильтрации VкрH (рис.1.2). Зависимость скорости фильтрации от градиента давления (рис.1.2) может использоваться для качественного установления вида закона фильтрации. Нелинейные законы фильтрации при больших скоростях фильтрации, например, при фильтрации газа, наиболее часто описываются двучленной формулой, которая для прямолинейно-параллельного течения без учета сит тяжести имеет вид где ρ- плотность жидкости или газа, кг/м3; β – константа пористой среды, связанная с микрошероховатостью и извилистостью поровых каналов, определяемая экспериментально, м. В уравнении (1.9) первое слагаемое в правой части учитывает потери давления из-за вязкости жидкости (трения), второе - за счет действия сил инерции, связанных с криволинейностью и извилистостью поровых каналов. Закон Дарси является частным случаем двучленного закона фильтрации, когда вторым членом в (1.9) можно пренебречь. Отметим, что нарушение линейного закона фильтрации еще не означает переход от ламинарного режима движения флюидов в пористой среде к турбулентному режиму. В подземной гидромеханике для характеристики закона движения флюидов в пористой среде по аналогии с трубной гидравликой используют безразмерный параметр - число Рейнольдса, которое по физическому смыслу представляет собой отношение сил инерции к силам вязкостного трения: Re =Vdρ/μ , (1.10) где d - некоторый характерный линейный параметр пористой среды, м; V - характерная скорость, м/с: ρ - плотность жидкости, кг/м': μ - коэффициент динамической вязкости жидкости, Па-с. Задачи лабораторной работы: 1) изучение распределения давления по длине линейного пласта при фильтрации несжимаемой жидкости; 2) изучение распределения градиента давления и скорости фильтрации по длине линейного пласта при фильтрации несжимаемой жидкости; 3) определение объемного расхода жидкости в потоке; 4) определение закона движения частиц жидкости и средневзвешенного по объему перового пространства пластового давления; 5) определение минимальной верхнекритической скорости фильтрации жидкости, при которой нарушается закон Дарси. РАСЧЕТНАЯ ЧАСТЬ Исходные данные: Рк=8,4 МПа; Рr = 5,9 Мпа; Lk = 6 км; к= 0.2 мкм2; μ = 5 МПа*с; h =2 м; ρ = 960 кг/м3; m = 18 % 1. Градиент давления (в Па/м): gradP = d2P / dx= 2. Скорость фильтрации (в м/с) согласно закону Дарси равна: 3. Дебит галереи (объемный расход жидкости в м3/с) равен где F-площадь поперечного сечения пласта F = Bh=140*2=280 м2 4. Закон движения жидких частиц определяется : 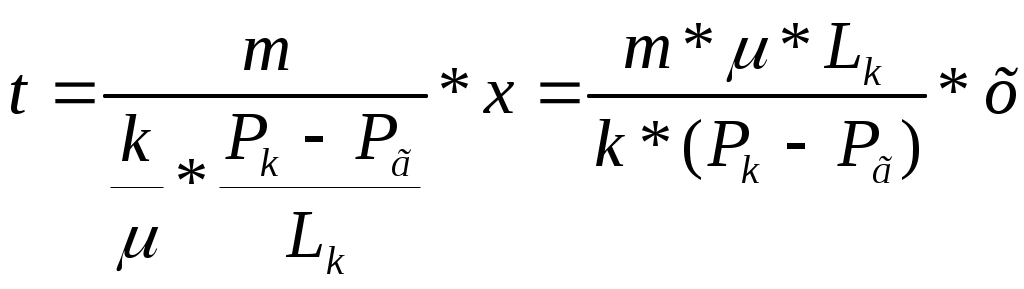 = = 5. Критическая скорость фильтрации: 6. Средневзвешенное по объему порового пространства пластовое давление: Вывод: Исследовали прямолинейно-паралельный установившийся фильтрационный поток несжимаемой жидкости в однородном пласте путем изучения: 1) распределения давления по длине линейного пласта при фильтрации несжимаемой жидкости; 2) распределения градиента давления и скорости фильтрации; 3) определения объемного расхода жидкости в потоке; 4) определения закона движения частиц жидкости и средневзвешанного по объему порового пространства пластового давления Лабораторная работа № 2 ИССЛЕДОВАНИЕ ПЛОСКОРАДИАЛЬНОГО УСТАНОВИВШЕГОСЯ ФИЛТРАЦИОННОГО ПОТОКА НЕСЖИМАЕМОЙ ЖИДКОСТИ В ОДНОРОДНОМ ПЛАСТЕ 2.1. Краткая теория вопроса Представим установившуюся фильтрацию жидкости к гидродинамически совершенной скважине радиусом rс, пробуренной в центре однородного но параметрам горизонтального кругового пласта с внешним радиусом Rh и постоянной толщиной h с непроницаемой кровлей и подошвой пласта, схематически представленного на рис. 2.1. 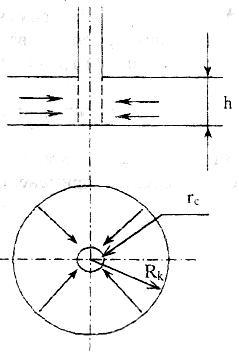 Рис. 2.1. Схема плоскорадиального потока Характерными особенностями такого потока являются: - во-первых, частицы жидкости движутся параллельно в одной и той же плоскости, проходящей через ось скважины; - во-вторых, прямолинейные траектории движения частиц жидкости в любой плоскости, перпендикулярной оси скважины, радиально сходятся в одной точке на оси скважины; - в-третьих, картины движения вдоль всех и любой траектории движения одинаковы, а следовательно для изучения такого потока достаточно изучить, движение вдоль одной любой траектории, т.е. поток является одномерным по радиусу. Такой установившийся фильтрационный поток называется одномерным плоскорадиальным и фильтрация в нем несжимаемой жидкости по закон Дарси в наиболее обшей форме описывается дифференциальным уравнением (2.1), которое в цилиндрических координатах имеет вид где Р – P(r) - давление на расстоянии r от оси скважины. Па; r - расстояние от оси скважины до рассматриваемой точки, м. Если заданы граничные условия, например, постоянное давление Р, на контуре питания радиуса Rс и забойное давление Рс на стенке скважины r, то, интегрируя уравнение (2.1), получают основные формулы, характеризующие остановившееся плоскорадиальное движение. 1. Распределение давления в круговом пласте: 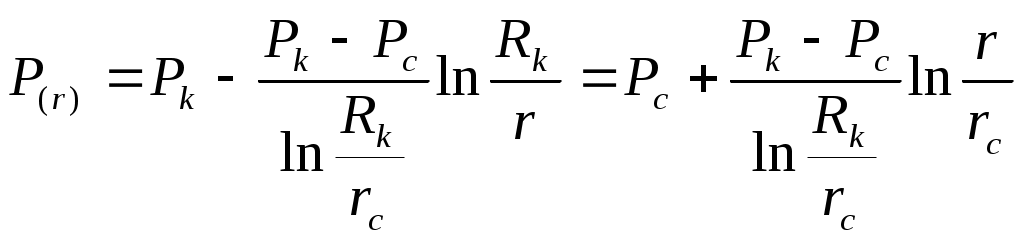 (2.2) (2.2)где P(r) - установившееся давление на расстоянии г от скважины. Па: Рк - установившееся контурное (пластовое) давление на контуре питания rk, Па; Рг - установившееся давление в скважине, Па; гс - радиус скважины, м; R- радиус контура питания пласта, м; r - текущий радиус, м. Из формулы (2.2) видно, что распределение давления представляет собой логарифмическую зависимость давления от радиуса и графически представляется логарифмической кривой. 2. Градиент давления gradP = dP / dr= 3. Скорость фильтрации 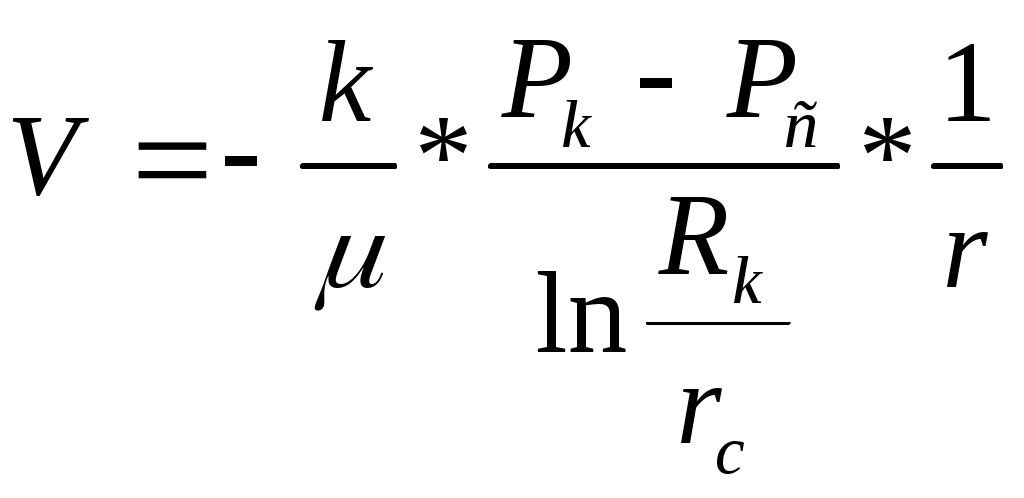 (2.4) (2.4)4 Дебит (объемный расход) скважины (по формуле Дюпюи) 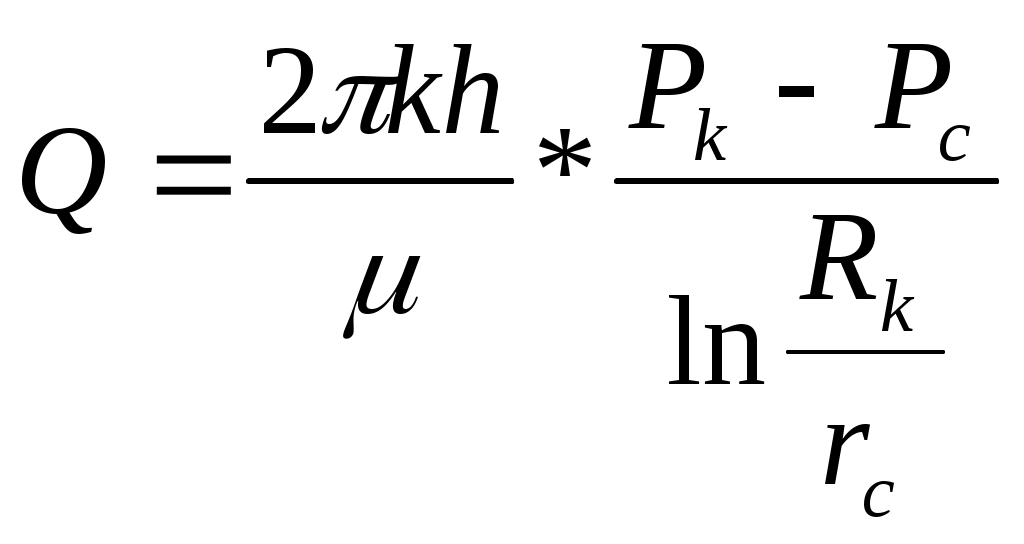 (2.5) (2.5)где Q - дебит скважины, м3/с; k - проницаемость пласта, м; h - толщина пласта, м: μ - динамическая вязкость, Па*с. 5. Закон движения частиц жидкости t = где r0 - начальное положение частицы жидкости; r - текущее положение частицы жидкости. 6. Время движения частицы жидкости от контура питания радиуса Rk забоя скважины радиуса rc T= 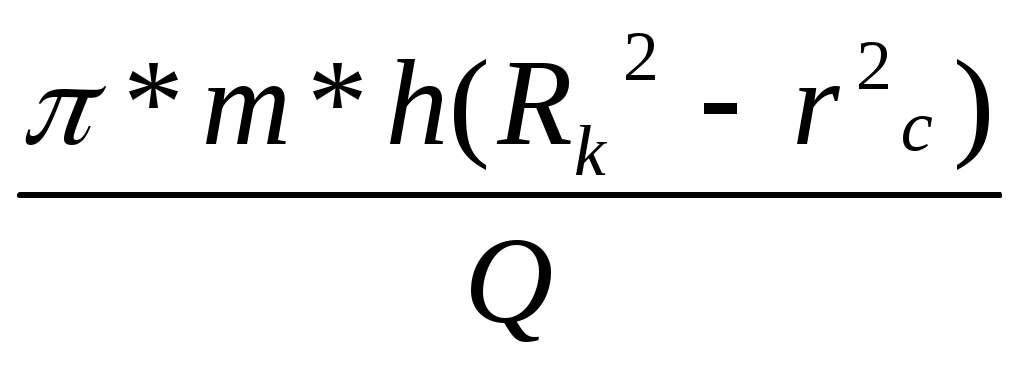 (2.7) (2.7)7. Средневзвешенное по объему перового пространства пластовое давление 8. Дебит скважины можно выразить в виде уравнения притока Q = K*ΔP, (2.8) K- коэффициент продуктивности скважины, м3/с*Па. В промысловых условиях часто используется размерность коэффициента продуктивности [К] – м3/(сут*МПа); Δр = рк - рс - депрессия на пласт, Па. Изучение особенностей плоскорадиальной фильтрации имеет большое практическое значение, т.к. приток нефти и газа к забоям эксплуатационных гидродинамически совершенных скважин подчиняется законам плоско-радиальной фильтрации. РАСЧЕТНАЯ ЧАСТЬ Исходные данные: Рк=8,4 МПа; Рс = 5,9 МПа; Rк = 1400 м; rc= 0.14 м; μ = 5 мПа*с; h =2 м; ρ = 960 кг/м3; m = 18 %; к = 0.2 мкм2 1. Дебит (объемный расход) скважины (по формуле Дюпюи): 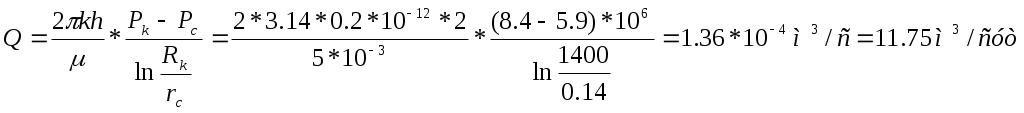 2. Средневзвешенное по объему перового пространства пластовое давление: 2. Средневзвешенное по объему перового пространства пластовое давление: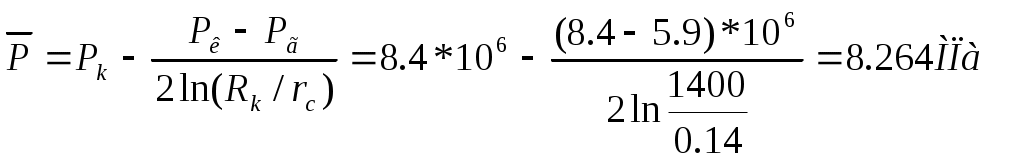 3. Время движения частицы жидкости от контура питания радиуса Rk забоя скважины радиуса rc: T= 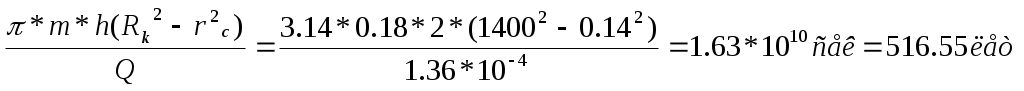 4. Коэффициент продуктивности: 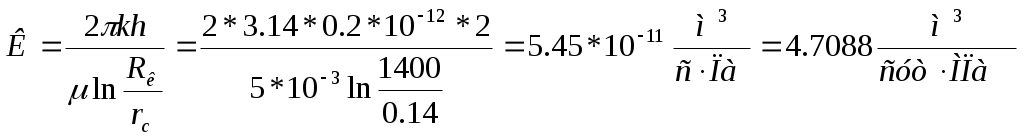 5. Коэффициент гидропроводности 6. Коэффициент проницаемости Вывод: Исследовали радиально-сферический установившийся фильтрационный поток несжимаемой жидкости в однородном пласте путем изучения: 1) распределения приведенного давления, градиента давления и скорости фильтрации в залежи круговой формы при фильтрации несжимаемой жидкости по закону Дарси; 2) определения дебита скважины , средневзвешанного по объему порового пространства пластового давления и время движения частицы от контура питания до центра забоя скважины. Лабораторная работа №3 ИССЛЕДОВАНИЕ РАДИАЛЬНО- СФЕРИЧECKOГО УСТАНОВИВШЕГОСЯ ФИЛЬТРАЦИИ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ОДНОРОДНОМ IIJIACTЕ 3.1. Краткая теория вопроса Представим установившуюся фильтрацию жидкости к скважине, вскрывшей однородный пласт весьма большой (теоретически бесконечной) толщины, через полусферический забой, радиус которого равен радиуса скважины rс, пробуренной в однородном по параметрам горизонтальном круговом пласте с внешним радиусом RK с непроницаемой кровлей пласта, схематически представленного на рис. 3.1. 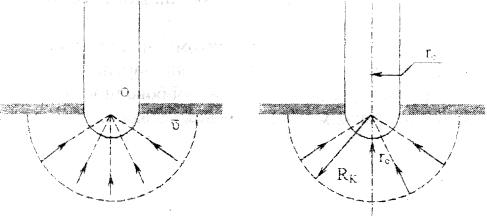 Рис. 3.1. Схема радиально-сферического фильтрационного потока Характерными особенностями такого потока являются: - во-первых, частицы жидкости движутся прямолинейно и их траектории радиально сходятся в центре полусферического забоя, в точке О. - во-вторых, в таком установившемся потоке напор и скорость фильтрации в любой его точке будут функцией только расстояния этой точки от центра забоя скважины, а следовательно поток является одномерным. Такой установившийся фильтрационный поток называется радиально-сферическим. Если заданы граничные условия, например, постоянное приведенное швление Рк на контуре питания радиуса RK. и приведенное давление на забое скважины Ре радиуса гс, то, интегрируя уравнение, получают основные формулы, характеризующие установившееся радиально-сферическое движение. 1. Распределение приведенного давления в радиально-сферическом фильтрацией ном потоке несжимаемой жидкости P*=P*k- 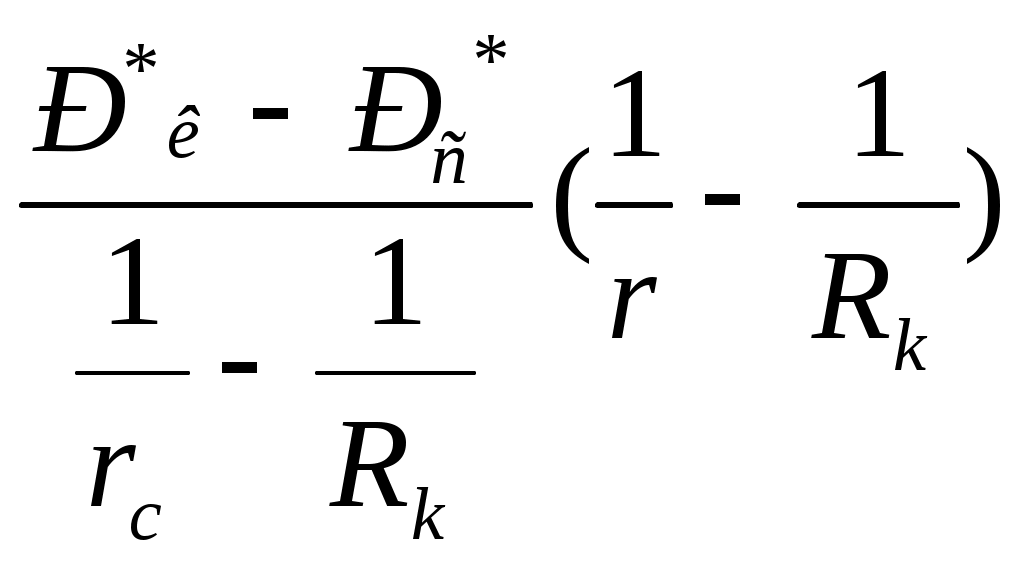 , (3.1) , (3.1)где Р - приведенное давление на расстоянии r от точки О скважины, Па; Р к -приведенное давление на контуре питания, Па; Р c* -приведенное давление на забое скважины, Па; rс - радиус скважины, м; RK - радиус контура питания, м; r - текущий радиус, м. Из формулы (3.1) следует, что приведенное давление в любой точке пласта обратно пропорционально координате г этой точки. Значит зависимость приведенного пластового давления от т гиперболическая. Поверхности равного приведенного давления (равного напора) представляют собой концентричные полусферы. Понятно, что в разных точках одной и той же поверхности равного напора истинные давления будут различны. Но, зная высотную отметку точки пласта, плотность пластовой жидкости, распределение приведенных пластовых давлений, легко *4айти истинное давление в любой точке пласта. 2. Градиент приведенного давления gradP* = 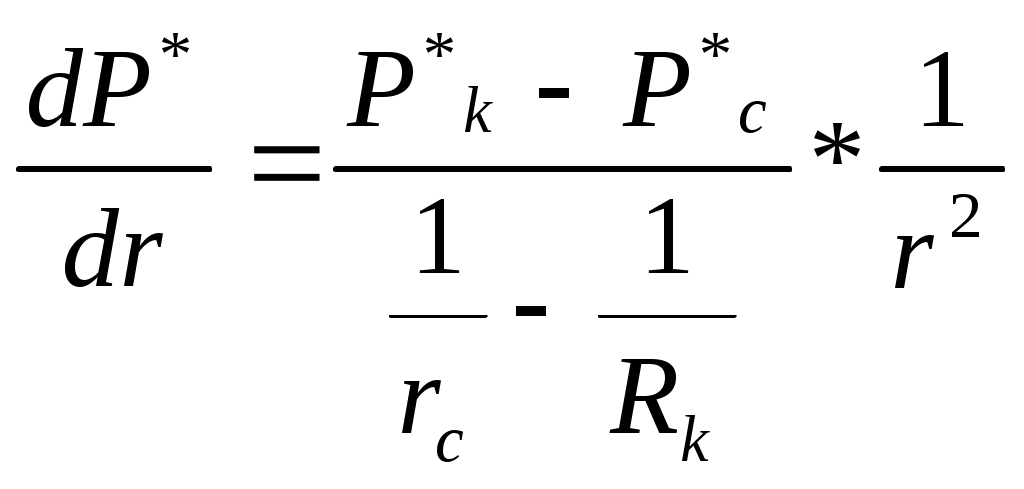 (3.2) (3.2)3. Скорость фильтрации 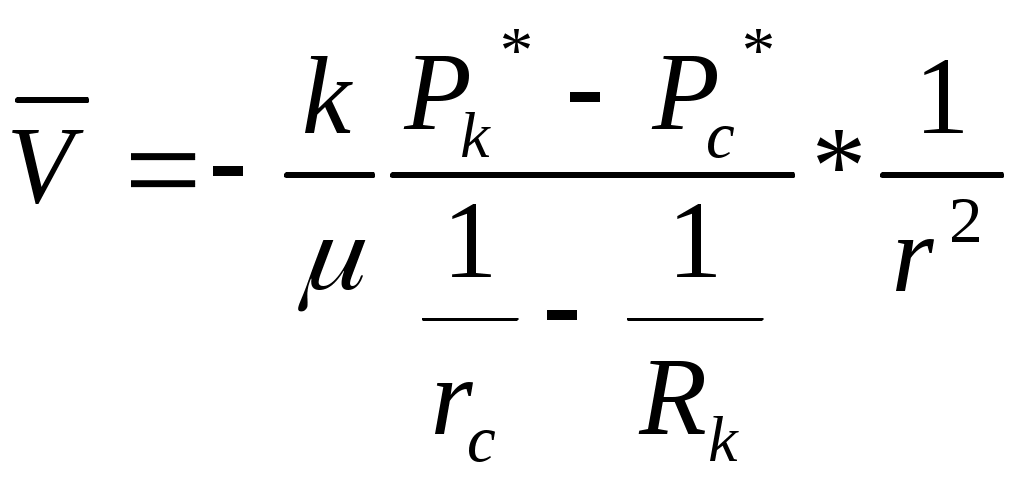 (3.3) (3.3)Формулы (4.3) и (4.4) свидетельствуют о том, что градиент приведенного давления и скорость фильтрации в любой точке пласта обратно пропорциональны квадрату расстояния этой точки от забоя скважины, cледовательно, если построить для радиально-сферического потока графики зависимости градиента приведенного давления и скорости фильтрации от текущего радиуса r, то крутизна соответствующей кривой у стенки скважины (при малых значениях r) в радиально-сферическом потоке будет еще больше, чем и плоскорадиальном. 4. Дебит (объемный расход) добывающей скважины радиусом r, 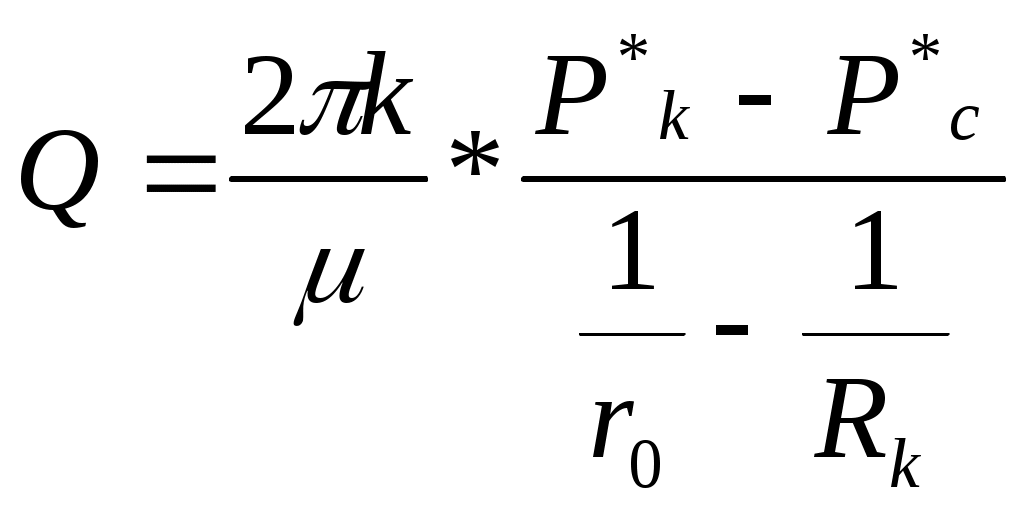 (3.4) (3.4)где Q-дебит скважины, м3/с: k - проницаемость пласта, м; μ - динамическая вязкость. Па*с. Как следует из формулы (3.4), зависимость дебита от перепада приведенного давления в радиально-сферическом потоке такая же, как и в плоскорадиальном потоке, следовательно, и форма индикаторной линии здесь будет тоже прямой . 5 Закон движения частиц жидкости вдоль их траекторий г где Ro- начальное положение частицы жидкости; r - текущее положение частицы жидкости. 6. Время движения частицы жидкости от контура питания радиуса Rk до центра забоя скважины радиуса гс T = 7. Средневзвешенное по объему порового пространства приведенное пластовое давление P*=P*k 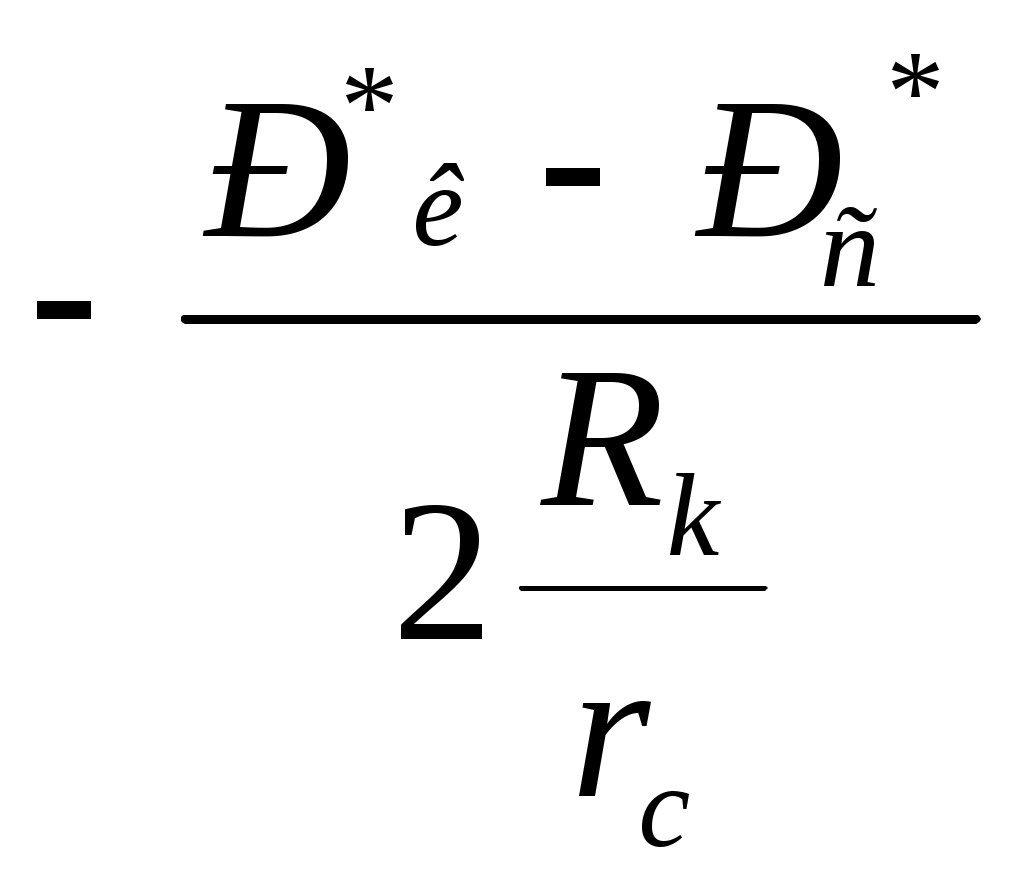 , (3.7) , (3.7) |
