Лабы подземка. Лабы-подземка. Лабораторная работа 1 исследование прямолинейнопаралельного установившегося фильтрационного потока несжимаемой
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
РАСЧЕТНАЯ ЧАСТЬ Исходные данные: Рк=8,4 МПа; Рс = 5,9 МПа; Rк = 1400 м; rc= 0.14 м; μ = 5 мПа*с; ρ = 960 кг/м3; m = 18 %; к = 0.2 мкм2 1. Дебит (объемный расход) добывающей скважины: 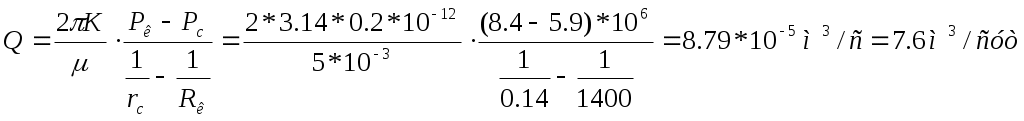 2. Время движения частицы жидкости от контура питания радиуса Rk до центра забоя скважины радиуса гс: 3. Средневзвешенное по объему порового пространства приведенное пластовое давление: P*=P*k 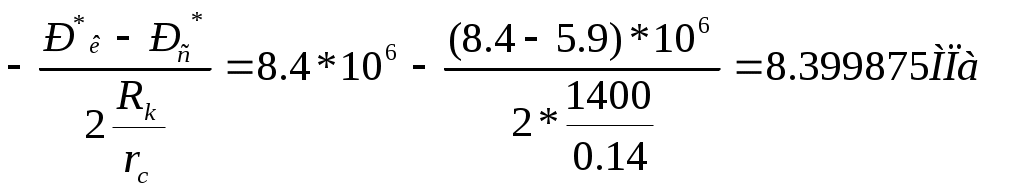 Вывод: Исследование радиально-сферического установившегося фильтрационного потока несжимаемой жидкости в однородном пласте путем: 1) изучения распределения приведенного давления, градиента приведенного давления и скорости фильтрации в залежи круговой формы при установившейся фильтрации несжимаемой жидкости по закону Дарси; 2) определения дебита скважины, средневзвешенного по объему перового пространства приведенного пластового давления и времени движения частицы от контура питания до центра забоя скважины радиуса. Лабораторная работа №4 ИССЛЕДОВАНИЕ ОДНОМЕРНОГО ПРЯМОЛИНЕЙНО-ПАРАЛЛЕЛЬНОГО УСТАНОВИВШЕГОСЯ ФИЛЬТРАЦИОННОГО ПОТОКА НЕСЖИМАЕМОЙ ЖИДКОСТИ В НЕОДНОРОДНЫХ ПЛАСТАХ 4.1. Краткая теория вопроса Реальные продуктивные пласты нефтяных и газовых месторождений имеют неоднородное строение по фильтрационным параметрам пластов, в частности, неоднородность по проницаемости. Различают слоистую неоднородность (по толщине пласта - сложен пропластками различной проницаемости) и зональную неоднородность (по площади, по простиранию пласта, неоднородный пласт с закономерным изменением в каком-либо направлении и др.) В данной лабораторной работе изучаются особенности фильтрации в слоисто неоднородном целесообразном пласте, состоящем из двух пропластков с различной проницаемостью (|рис.4.1а) и зонально-неоднородном полосообразном пласте, состоящем из двух зон с различной проницаемостью (рис 4.1, б). 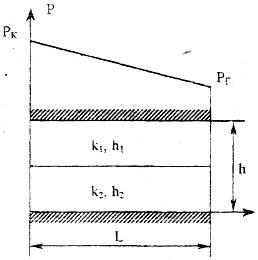 а) б) 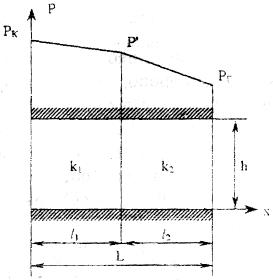 Рис. 4.1. Прямолинейно-параллельный поток в: а) слоисто-неоднородном б) зонально-неоднородном пластах Рассмотрим особенности фильтрации в слоисто- и зонально-неоднородных волосообразных пластах. а) случай слоисто-неоднородного пласта При стационарной одномерной прямолинейно-параллельной фильтрации несжимаемой жидкости по закону Дарси в слоисто-неоднородном пласте. состоящем из 2-х пропластков с различной проницаемостью К1 и К2(Рис 4.1, а). распределение давления в каждом из пропластков линейное и определяется выражением где Рк - контурное давление, Па; Рг - давление на галерее. Па; L - длина пласта, м. Градиенты давления в каждом пропластке постоянны и равны между собой, поскольку Скорости фильтрации по пропласткам: где μ - динамическая вязкость, Па*с. При равенстве градиентов давления в каждом пропластке из уравнений (5.3)-(5.4) следует справедливость следующего соотношения : V1/V2=K1/K2 (4.4) т.е. для слоисто-неоднородного пласта скорости фильтрации по пропласткам прямо пропорциональны проницаемостям. Различие скоростей фильтрации V по пропласткам крайне нежелательно. Стремятся к тому, чтобы нефть двигалась к пропласткам с одинаковой скоростью. Для этого регулируют продвижение фронта нагнетания воды. Дебит потока Q можно вычислить как сумму дебитов в отдельных пропластах Qi: где B- ширина залежи, м; h – толщина пласта, м Средний коэфициент проницаемости полосообразной залежи: kcp=∑kh/ ∑ h(4.6) б) случай зонально-неоднородного пласта При стационарной одномерной прямолинейно-параллельной фильтрации несжимаемой жидкости по закону Дарси в зонально-неоднородном пласте, состоящем из 2-х однородных зон с различной проницаемостью Ki и К2 (рис 5.1 б), распределение давления в каждом из пропластков линейное, но определяется следующими выражениями: где Р - давления на границе 1 и 2 зон; l1 и l2 - протяженности 1 и 2 зон, м. Градиенты давления в каждой зоне постоянны, но не равны между собой, поскольку gradP1 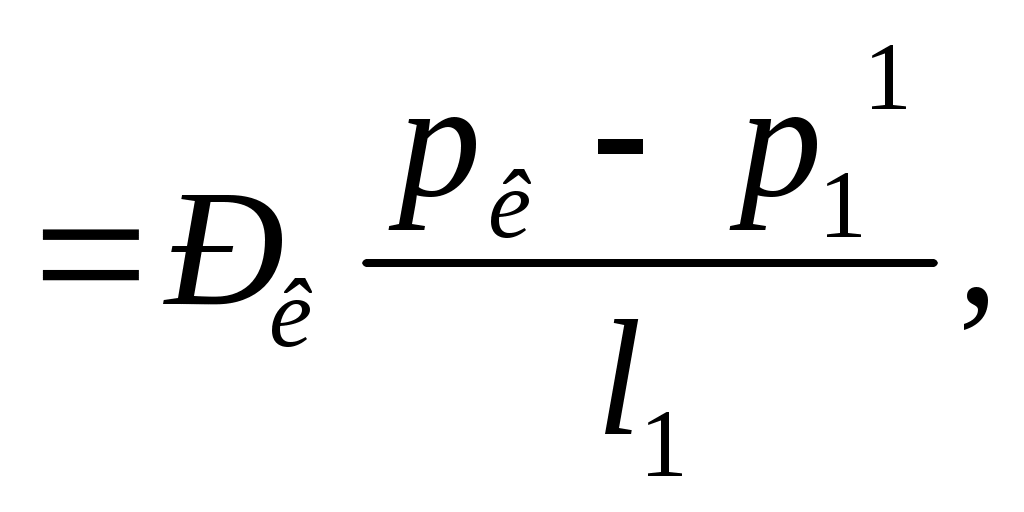 (4.9) (4.9)gradP2 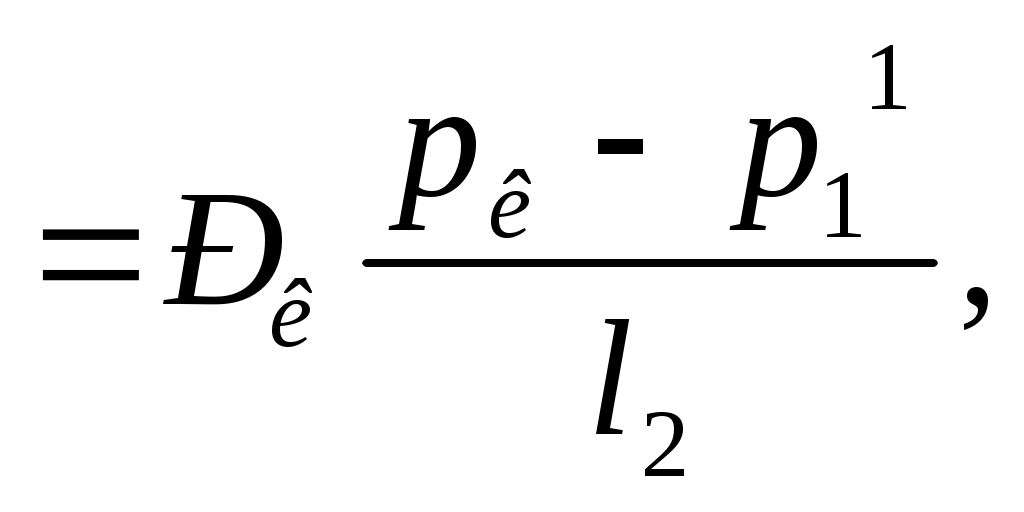 (4.10) (4.10)Скорости фильтрации по пропласткам: Из уравнения неразрывности фильтрационного потока следует, что объемные расходы по зонам и по всей полосообразной залежи одинаковы, т.е. Q =V1F1= V2F2 означает, что V1=V2, т.к. F1=F2=B*h. РАСЧЕТНАЯ ЧАСТЬ Исходные данные: Рк=8,4 МПа; Рс = 5,9 МПа; Lк = 6 км; В = 140 м; h = 2 м; μ = 5 мПа*с; к1 = 0,2 мкм2; к2 = 0,9 мкм2; h1 = 3 м; h2 = 4 м; l1 = 3 км; l2 = 3 км а) случай слоисто-неоднородного пласта 1. Градиенты давления в каждом пропластке постоянны и равны между собой, поскольку 2. Скорости фильтрации по пропласткам: 3. При равенстве градиентов давления в каждом пропластке следует справедливость следующего соотношения : V1/V2=K1/K2 =1,68*10-9/7,56=0,2/0,9=0,22 gradP1/ gradP2=K2/K1=700/133,3=0,9/0,2=4,5 4. Дебит потока Q можно вычислить: Q=Q1+Q2=4.2 м3/сут 5. Средний коэфициент проницаемости полосообразной залежи: kcp=∑kh/ ∑ h=(0,2*3+0,9*4)/7=0,7 мкм2 6. Средневзвешенное по объему порового пространства приведенное пластовое давление P*= Q1= Q1= Q= Q1= Q2 Q= kcp= 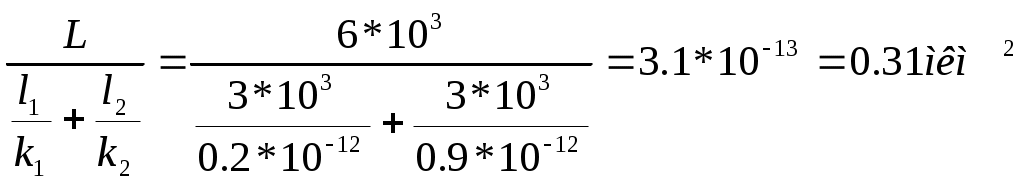 Вывод: Исследование одномерного прямолинейно-параллельного установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах для: 1) изучения влияния изменения проницаемости на распределение давления в слоисто- и зонально-неоднородных полосообразных пластах при установившейся фильтрации в них несжимаемой жидкости: 2) изучение характера распределения градиента давления и скорости фильтрации по длине слоисто- и зонально-неоднородных пластов при установившейся фильтрации в них несжимаемой жидкости; 3) определение средней проницаемости слоисто- и зонально-неоднородного пласта. Лабораторная работа №5. ИССЛЕДОВАНИЕ ОДНОМЕРНОГО ПЛОСКОРАДИАЛЬНОГО УСТАНОВИВШЕГОСЯ ФИЛЬТРАЦИОННОГО ПОТОКА НЕСЖИМАЕМОЙ ЖИДКОСТИ В НЕОДНОРОДНЫХ ПЛАСТАХ 5.1. Краткая теория вопроса 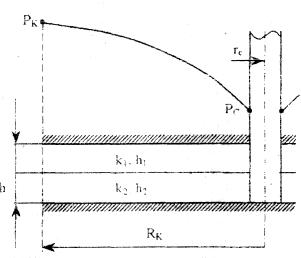 В данной лабораторной работе изучаются особенности фильтрации в слоисто-неоднородном круговом пласте, состоящем из двух пропластков с различной проницаемостью (рисунок , а) и зонально-неоднородном круговом пласте, состоящем из двух зон с различной проницаемостью (Рис 5.1. б). 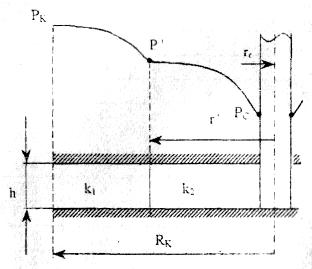 Рисунок 6.1 Плоскорадиальный поток в : а) слоисто-неоднородном б) зонально-неоднородном пластах Рассмотрим особенности фильтрации в слоисто- и зонально-неоднородных круговых пластах. а) случай слоисто-неоднородного пласта 1. При стационарной одномерной плоскорадиальной фильтрации несжимаемой жидкости по закону Дарси в слоисто-неоднородном пласте, состоящем из 2-х пропластков с различной проницаемостью К1 и К2 (рисунок, а), распределение давления в каждом из пропластков носит логарифмический характер и определяется выражением 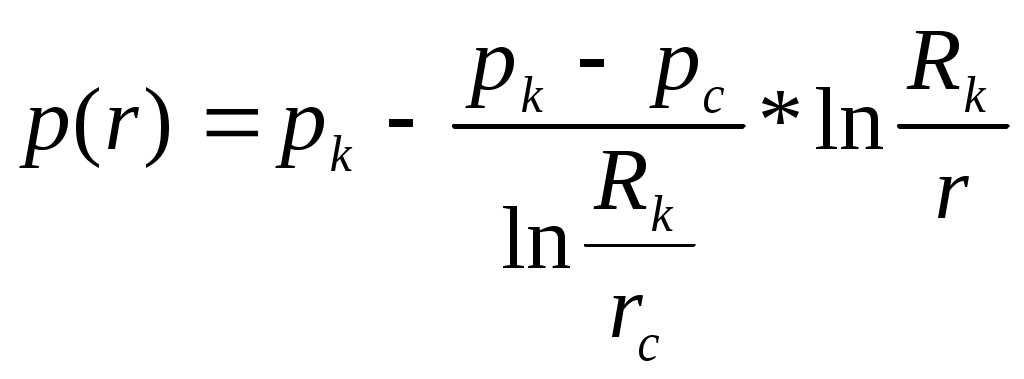 (5.1) (5.1)где Р(r) - установившееся давление на расстоянии г от скважины. Па; r - текущий радиус, м; Рк - установившееся пластовое давление на контуре питания rk, Па; Rк - радиус контура питания пласта, м; 2 Градиенты давления в каждом пропластке одинаковы и определяются следующим выражением: 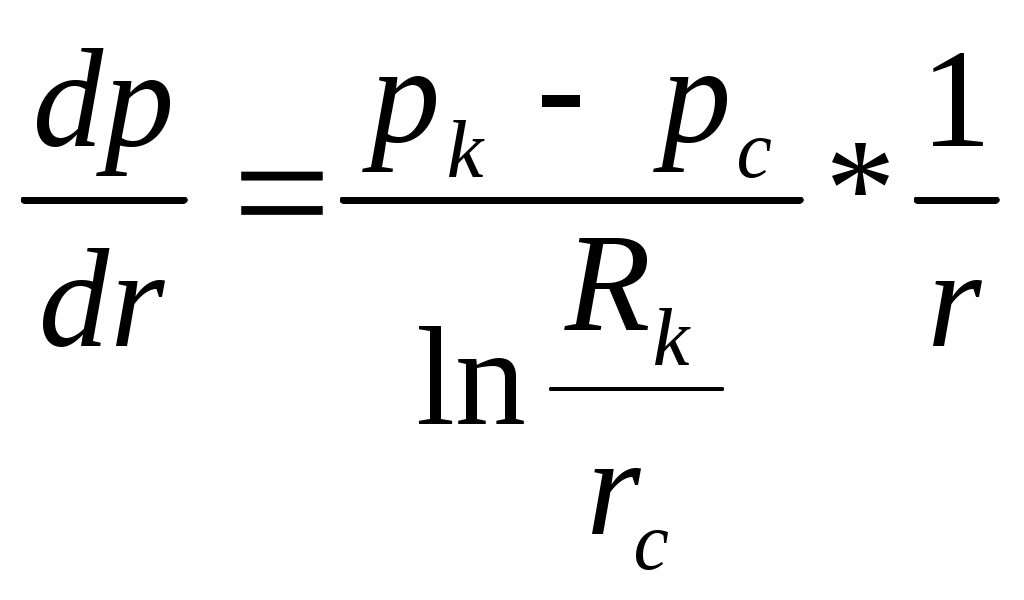 (5.2) (5.2)V Скорости фильтрации по пропласткам: 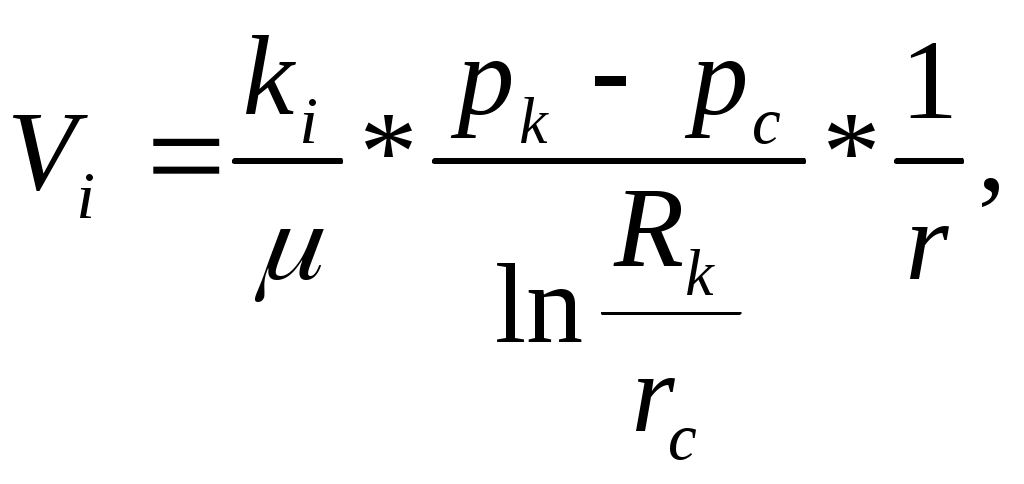 (5.3) (5.3)где μ - динамическая вязкость, Па*с. При равенстве градиентов давления в каждом пропластке из уравнений следует справедливость следующего соотношения: V1/V2=K1/K2 (5.4) т. е. для слоисто-неоднородного кругового пласта скорости фильтрации по пропласткам прямо пропорциональны проницаемостям. Т.о. жидкость будет двигаться с опережением по более нысокопроницаемому пропластку. Необходимо принимать меры по иыравниванию фронтов движения жидкостей в пропластках с различной проницаемостью. 4. Выразим дебит скважины Q для случая слоисто-неоднородного пласта через кср: 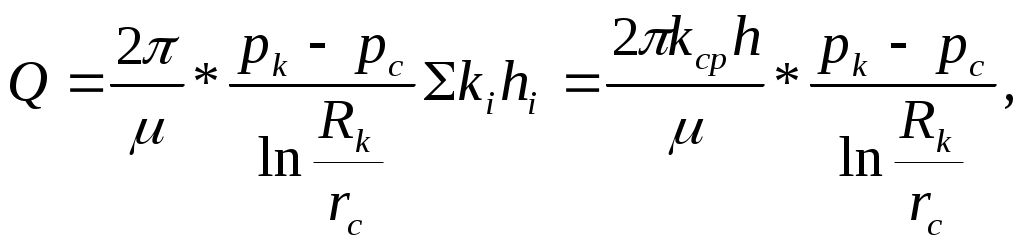 (5.5) (5.5)Средняя проницаемость в общем виде: kcp =∑kihi / h, (5.6) б) случай зонально-неоднородного пласта В практике разработки нефтяных и газовых месторождений значительный интерес представляет задача о притоке жидкости к скважине при наличии вокруг забоя скважины кольцевой зоны с проницаемостью, отличной от проницаемости остальной части пласта, т. е. пласт состоит из двух зон различной проницаемости. Такая задача возникает в следующих случаях: при торпедировании или кислотной обработке призабойной зоны, установке гравийного фильтра, глинизации или парафинизации призабойной зоны, выносе мелких фракций породы из этой зоны и т.д. Очень важной при этом бывает необходимость установления влияния различия проницаемостей кольцевой призабойной зоны и остальной части пласта на продуктивность скважины 1. При стационарной одномерной плоскорадиальной фильтрации несжимаемой жидкости по закону Дарси в зонально-неоднородном пласте, состоящем из 2-х зон с различной проницаемостью ki и к2 (рис. 5.1, б), распределение давления в каждой зоне подчиняется логарифмическому закону, но характер распространения пьезометрической линии зависит от давления Р' на границе этих зон: 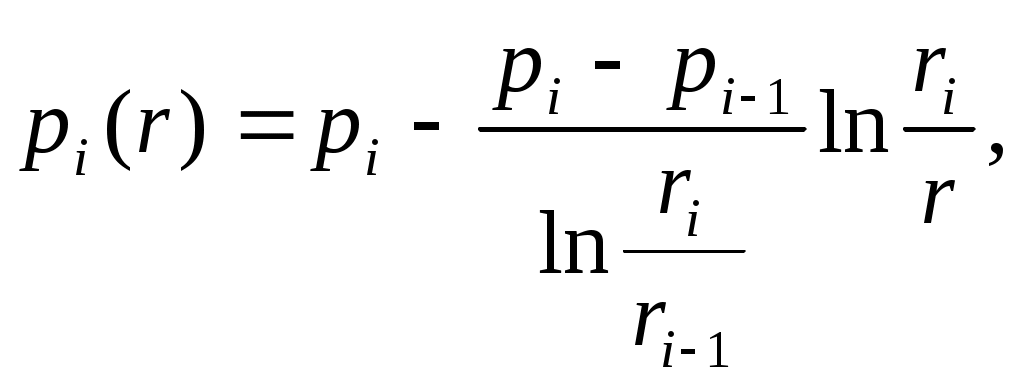 i=1,2,…,n, (5.7) i=1,2,…,n, (5.7)где r - текущий радиус, м: r! -радиус границы между первой и второй зоной, м; Рi-1 - давление на границе этих зон, Па; ri - радиус контура питания пласта, м: Рi - установившееся пластовое давление на контуре питания rk., Па: Распределение градиентов давления в каждой зоне подчиняется гиперболическому закону, но характер их распространения также зависит от давления Р' на границе этих зон: 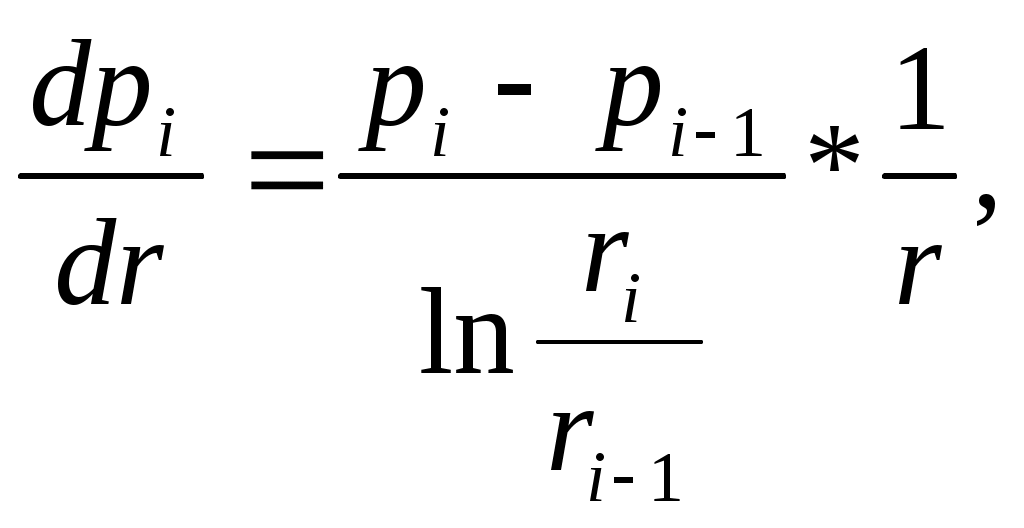 i=1,2,…,n, (5.8) i=1,2,…,n, (5.8)3. Скорости фильтрации по зонам прямо пропорциональны градиентам давления в зонах: 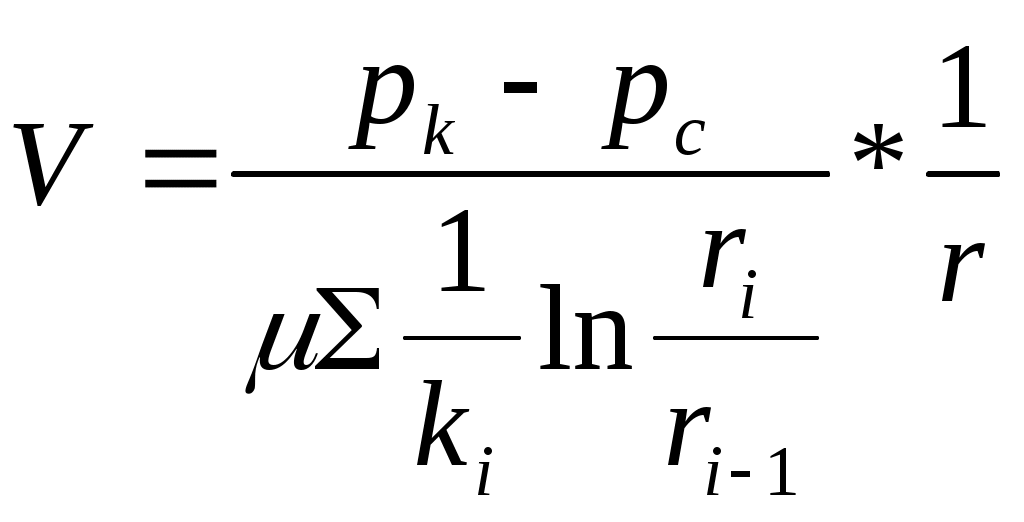 (5.9) (5.9)4. Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине: 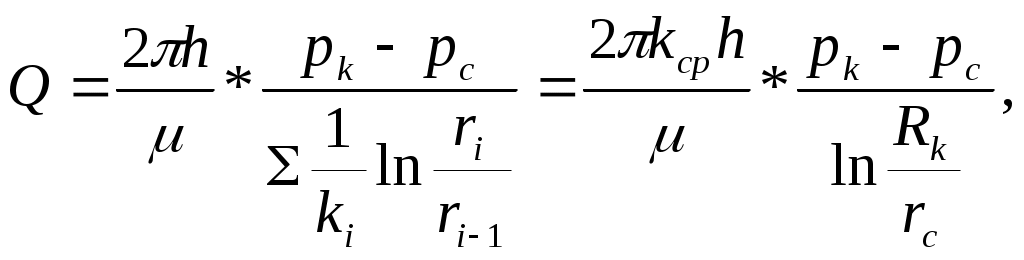 (5.10) (5.10)Среднее значение проницаемости определится:  (5.11) (5.11)РАСЧЕТНАЯ ЧАСТЬ Исходные данные: Рк=8,4 МПа; Рс = 5,9 МПа; Rк = 1400 м; rc = 0.140 м; μ = 5 мПа*с; к1 = 0,2 мкм2; к2 = 0,9 мкм2; h1 = 3 м; h2 = 4 м; r!=700 м а) случай слоисто-неоднородного пласта 1. Скорости фильтрации по зонам прямо пропорциональны градиентам давления в зонах: 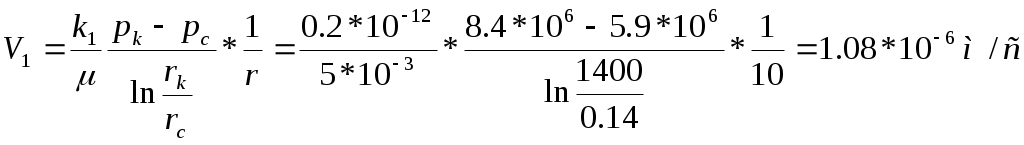 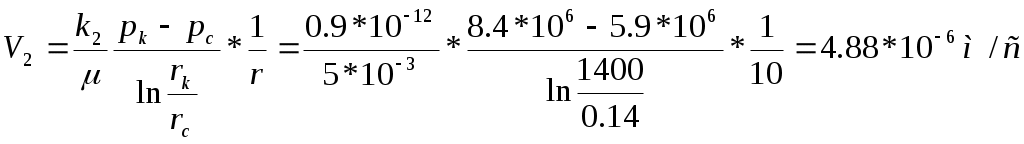 2. Среднее значение проницаемости определится: 3. Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине: 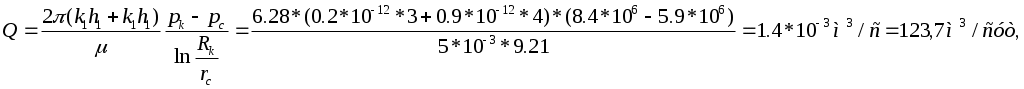 б) случай зонально-неоднородного пласта б) случай зонально-неоднородного пласта1. Средневзвешанное давление: 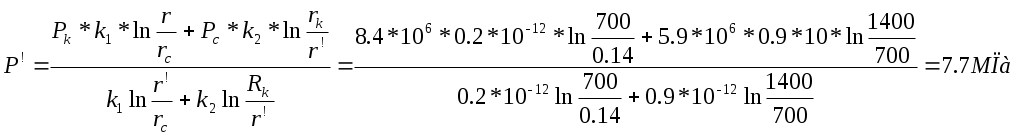 2. Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине: 2. Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине: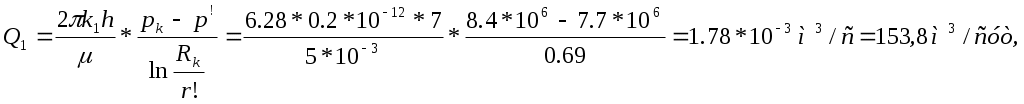 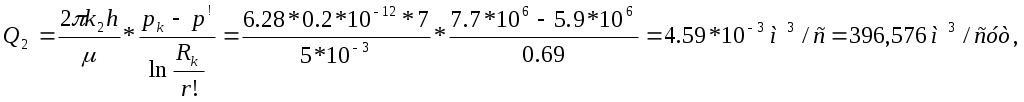 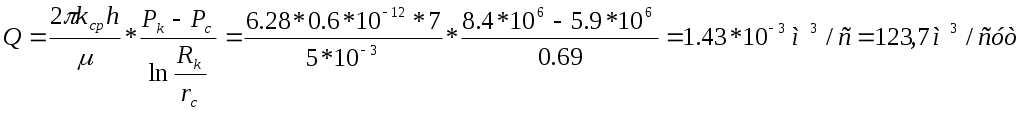 3. Среднее значение проницаемости определится: 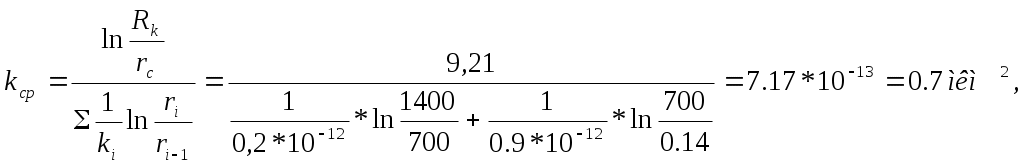 |
