Эконометрика. Пазий2lab. Лабораторная работа 2 Парная линейная регрессия. Мнк. Доверительные интервалы для коэффициентов регрессии Выполнил студент
 Скачать 93.98 Kb. Скачать 93.98 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Челябинский государственный университет» (ФГБОУ ВО «ЧелГУ») Лабораторная работа №2 Парная линейная регрессия. МНК. Доверительные интервалы для коэффициентов регрессии Выполнил студент: Игнатов Дмитрий Группы МП-402
Челябинск 2022 Парная линейная регрессия представляет собой зависимость между двумя переменными – y и x, т.е. модель вида y=f(x) или y=αx+β+ɛ, где у – зависимая переменная, х – независимая или объясняющая переменная, α и β – коэффициенты регрессии, ɛ - ошибка регрессии. Согласно методу наименьших квадратов, неизвестные параметры α и β выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений 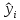 была минимальной. была минимальной.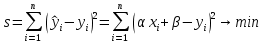 Создаем группу под названием par_regres из 300 элементов.  Создаем ряды Y1, Y2, копируем в них данные из таблицы. Проверяем, что все 300 элементов занесены в таблицу.  Создаем ряды для расчета оценок коэффициентов регрессии α и β, соответственно ряды А и B. Оценки коэффициентов парной линейной регрессии определяются методом наименьших квадратов и вычисляются по следующим формулам: 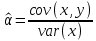 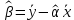 Пользуемся формулой и получаем: 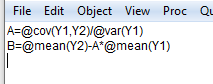 Создаем ряд Y2T для нахождения регрессионной прямой. Она находится по формуле: 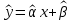 В строку формул вводим уравнение и получаем: 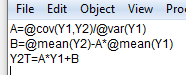 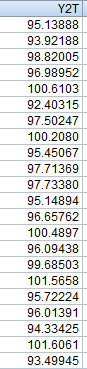 Доверительные интервалы для коэффициентов регрессии определяются следующим образом: 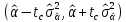 – доверительный интервал для α – доверительный интервал для α 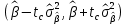 – доверительный интервал для β – доверительный интервал для βГде tc – табличное значение статистики Стьюдента. При числе степеней свободы более 200 tc будет равно: 1.645 на 10% уровне значимости, 1.96 – на 5% уровне значимости, 2.576 – на 1% уровне значимости. Создаем ряды DY2, DA, DB для расчета величин 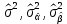 . . 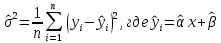 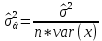 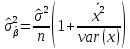 Переносим эти формулы в строку ввода:  Создаем ряды А1, А2, В1, В2 для расчета границ доверительных интервалов с надежностью 0.9 и получаем:  Аналогично рассчитаем границы доверительных интервалов с надежностью 0.95 и 0.99 соответственно:   |
