Лабораторная работа 215 2 свободные колебания в контуре 2 вынужденные колебания в rlc контуре

• Название: Лабораторная работа 215 2 свободные колебания в контуре 2 вынужденные колебания в rlc контуре
• Дата: 28.12.2022
• Размер: 153.12 Kb.
• Имя файла: LABORATORNAYa_RABOTA_215.docx
• Тип: Лабораторная работа; #867990

ЛАБОРАТОРНАЯ РАБОТА № 215

2_6. СВОБОДНЫЕ КОЛЕБАНИЯ В КОНТУРЕ

2_7. вынужденные колебания в rlc-контуре

Ознакомьтесь с теорией в конспекте, учебнике (Савельев, т. 2, § 89, § 90). Запустите программу. Выберите «Электричество и магнетизм» и «Свободные колебания в RLC–контуре». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ с. 5 еще раз.)

ЦЕЛЬ РАБОТЫ:

1. 
   Знакомство с компьютерной моделью процесса свободных затухающих колебаний в электрическом колебательном контуре.
   
2. 
   Экспериментальное исследование закономерностей свободных затухающих колебаний.
   
3. 
   Экспериментальное определение величины индуктивности контура.
   
4. 
   Знакомство с компьютерным моделированием процессов в колебательном RLC-контуре.
   
5. 
   Экспериментальное подтверждение закономерностей при вынужденных колебаниях в RLC-контуре.
   
6. 
   КРАТКАЯ ТЕОРИЯ:
   
7. 
   КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах.
   
8. 
   НАПРЯЖЕНИЕ НА КОНДЕНСАТОРЕ: .
   
9. 
   ЭДС самоиндукции в катушке: .
   
10. 
    НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ: .
    
11. 
    ОПРЕДЕЛЕНИЕ ТОКА: .
    
12. 
    ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных незатухающих колебаний:
    
13. 
    , где ₀ = – собственная частота контура .
    
14. 
    Период: Т = 2 .
    
15. 
    Его решение q(t) = q_v cos(₀ t + ), где  – начальная фаза.
    
16. 
    ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний
    
17. 
    , где  = – коэффициент затухания.
    
18. 
    Его решение: q(t) = q_v0 е^-t cos(t + ), где – частота затухающих колебаний.
    
19. 
    ПОСТОЯННАЯ ВРЕМЕНИ ЗАТУХАНИЯ в контуре  есть время, за которое амплитуда колебаний уменьшается в е = 2,73 раз. На графике зависимости амплитуды затухающих колебаний от времени касательная, проведенная к этому графику в начальный момент времени, пересекает ось времени в точке t = .
    
20. 
    q(t)
    
21. 
    А₁
    
22. 
    А₂ ---- касательная
    
23. 
    А₃
    
24. 
    
    
25. 
    t
    
26. 
    t₂ = Т t₃ = 2Т
    
27. 
    
    
28. 
    ЛОГАРИФМИЧЕСКИМ ДЕКРЕМЕНТНОМ ЗАТУХАНИЯ называется величина, определяемая формулой . ДОБРОТНОСТЬ контура равна Q = .
    
29. 
    Повторите основные определения для колебательного движения, которые приведены в ЛР 1_4. Прочитайте также снова теорию к ЛР 2_3, в которой рассмотрены свободные колебания в контуре.
    
30. 
    ВЫНУЖДЕННЫМИ КОЛЕБАНИЯМИ называются процессы, происходящие в контуре, содержащем конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС, включенные последовательно и образующие замкнутую электрическую цепь.
    
31. 
    Если ЭДС источника меняется по гармоническому закону, то в контуре наблюдаются вынужденные гармонические колебания. При этом ток в контуре также будет переменным, подчиняющимся закону Ома в комплексной форме.
    
32. 
    КОМПЛЕКСНАЯ ВЕЛИЧИНА есть определенная совокупность двух алгебраических чисел , где А – действительная часть, В – мнимая часть, Z – модуль,  – фаза комплексной величины. Графически изображается, как радиус-вектор на комплексной плоскости: его длина равна Z, а угол между вектором и горизонтальной (действительной) осью равен .
    
33. 
    КОМПЛЕКСНЫЙ ТОК и КОМПЛЕКСНОЕ НАПРЯЖЕНИЕ
    
34. 
    – это векторы, которые вращаются с угловой скоростью .
    
35. 
    Здесь – комплексная амплитуда напряжения;
    
36. 
    – комплексная амплитуда тока.
    
37. 
    и – комплексные векторы, которые на комплексной плоскости неподвижны. Они соответствуют «мгновенной фотографии» реальных комплексных токов и напряжений, сделанной в начальный момент времени (t = 0).
    
38. 
    Комплексная амплитуда – сама комплексная величина, взятая в начальный момент времени.
    
39. 
    М атематически:
    
40. 
    (импеданс), Z
    
41. 
    
    
42. 
    
    
43. 
    Импеданс – это отношение комплексной амплитуды напряжения на данном элементе, к комплексной амплитуде тока через данный элемент.
    
44. 
    Модуль импеданса называется ПОЛНЫМ ЭЛЕКТРИЧЕСКИМ СОПРОТИВЛЕНИЕМ цепи.
    
45. 
    ;
    
46. 
    а) Резистор: ; ; фазы напряжения и тока одинаковые. Импеданс равен R: Z_R ≡ X_R = R .
    
47. 
    б) Катушка индуктивности: Действует закон электромагнитной индукции (самоиндукции): .
    
48. 
    Использовав его и закон Ома для комплексных величин, получим:
    
49. 
    ;
    
50. 
    
    
51. 
    – импеданс катушки индуктивности.
    
52. 
    Напряжение на катушке опережает по фазе ток через нее на /2.
    
53. 
    в) Конденсатор: или .
    
54. 
    Пусть тогда .
    
55. 
    Найдем отношение отсюда
    
56. 
    – ­ комплексное сопротивление (импеданс) конденсатора.
    
57. 
    Напряжение на конденсаторе отстает по фазе от тока через него на /2.
    
58. 
    
    
59. 
    Модуль комплексного сопротивления (катушки или конденсатора) называется РЕАКТИВНЫМ СОПРОТИВЛЕНИЕМ (индуктивным или емкостным). Обозначается символом без крышечки над ним.
    
60. 
    
    
61. 
    Все элементы в контуре соединены последовательно, поэтому для нахождения импеданса контура надо просуммировать импедансы всех элементов:
    
62. 
    . После подстановки можем получить модуль импеданса, то есть полное сопротивление контура:
    
63. 
    .
    
64. 
    РЕЗОНАНСОМ для тока называется явление резкого увеличения амплитуды колебаний тока при приближении частоты ЭДС к некоторому значению, называемому резонансной частотой _РЕЗ . Нетрудно видеть, что максимум амплитуды тока будет тогда, когда минимально полное сопротивление контура, или Z_РЕЗ = R и , отсюда , что соответствует частоте свободных колебаний в контуре.
    
65. 
    Максимум напряжения на конденсаторе соответствует резонансу для напряжения, который наблюдается при несколько меньшей частоте ЭДС: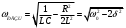
    
66. 
    .
    
67. 
     = – коэффициент затухания для данного контура.
    
68. 
    Амплитуда резонансного напряжения на конденсаторе U_0C пропорциональна амплитуде ЭДС и добротности контура Q: U_0C = Q  ₀.
    
69. 
    При не слишком большом затухании в контуре добротность определяется соотношением
    
70. 
    , где 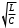 = называется характеристическим сопротивлением контура. Чем больше добротность, тем «острее» резонанс.
    
71. 
    РЕЗОНАНСНОЙ КРИВОЙ называется зависимость амплитуды напряжения на конденсаторе от частоты ЭДС.
    

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.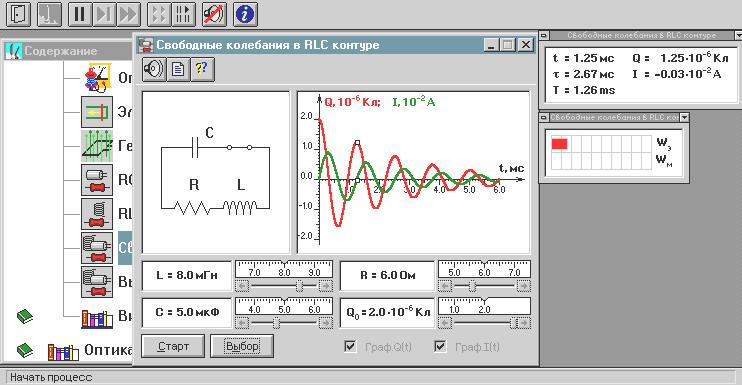



Получите у преподавателя допуск для выполнения измерений.
ИЗМЕРЕНИЯ:

1. 
   Нажмите мышью кнопку «Выбор». Подведите маркер мыши к движку регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину емкости конденсатора и установите числовое значение, равное взятому из табл. 1 для вашей бригады. Аналогичным способом установите величину индуктивности в соответствии с табл. 1.
   
2. 
   Установите сопротивления резистора R = 1 Ом. Нажав кнопку «Старт», наблюдайте график зависимости заряда конденсатора от времени. Измерьте линейкой значения первых шести амплитуд и запишите их в табл. 2. Меняя сопротивление R, повторите измерения амплитуд и заполните таблицу 2.
   

ТАБЛИЦА 1. Значения емкости конденсатора и индуктивности катушки (не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
С, мкФ	3	3	2,7	2,7	2,4	2,4	2	2
L, мГн	6	7	8	9	10	9	8	7

ТАБЛИЦА 2. Результаты измерений при С = ____ мкФ, L = ____ мГн,

Т = ____ мс.

R Ом	А1 мм	А2 мм	А3 мм	А4 мм	А5 мм	А6 мм	 мс	 с-1
1
2
3
4
5
6
t, мс

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

1. 
   Рассчитайте значения периода колебаний и запишите в заголовке табл. 2.
   
2. 
   Рассчитайте время t, при котором измерена соответствующая амплитуда и запишите в табл. 2.
   
3. 
   Постройте на одном чертеже графики экспериментальных зависимостей амплитуды колебания А от времени t (6 линий, соответствующих разным R).
   
4. 
   Для каждого графика постройте касательную к нему в начальный момент времени. Продолжив касательную до пересечения с осью времени, определите экспериментальное значение постоянной времени затухания  и запишите в табл. 2.
   
5. 
   Рассчитайте величины коэффициента затухания  = 1/ и также внесите в табл. 2.
   
6. 
   Постройте график зависимости коэффициента затухания от сопротивления резистора.
   
7. 
   По графику (R) определите индуктивность контура, используя формулу .
   
8. 
   Запишите ответ и сформулируйте выводы по ответу и графикам.
   

Закройте окно теории. Внимательно рассмотрите рисунок для компьютерной модели.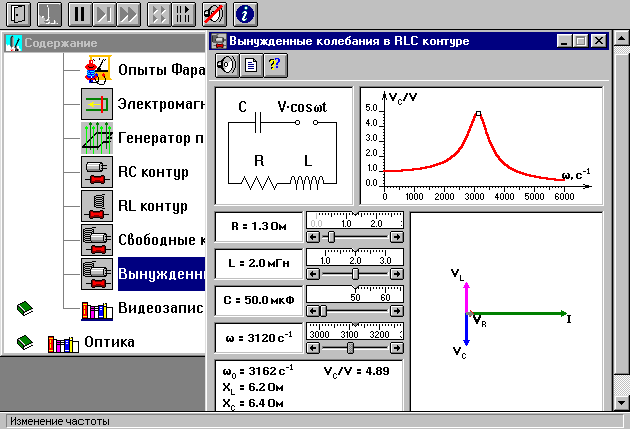


Перерисуйте необходимое в конспект, используя обозначения, принятые в нашей теоретической части (₀ вместо V, U_0C вместо V_C , U_0L вместо V_L и U_0R вместо V_R).

Подготовьте табл. 1, используя образец. Подготовьте также табл. 3 и 4, аналогичные табл.1.

ТАБЛИЦА 1. результаты измерений (12 столбцов). L = ____ мГн								ТАБЛИЦА 2. Значения характеристик (не перерисовывать)
	C, мкФ =	50	55	...	100		Бригады		R, Ом	L1, мГн	L2, мГн	L3, мГн
	РЕЗ, 1/с						1 или 5		1 или 2	1,0	1,7	2,4
	0, 1/с						2 или 6		2 или 1	1,2	1,9	2,6
	U0C/0						3 или 7		1 или 2	1,4	2,1	2,8
	1/						4 или 8		2 или 1	1,6	2,3	3,0

Получите у преподавателя допуск для выполнения измерений.
ИЗМЕРЕНИЯ:

1. 
   Закройте окно теории (если вы ее вызывали), нажав кнопку в правом верхнем углу внутреннего окна. Изменяйте величину емкости конденсатора и наблюдайте изменение резонансной кривой.
   
2. 
   Зацепив мышью, перемещайте движки регуляторов:
   
   1. 
      R – сопротивления резистора,
      
   2. 
      L – индуктивности катушки,
      

и зафиксируйте значения, указанные в табл. 2 для вашей бригады.

3. 
   Установите указанное в табл. 1 значение емкости конденсатора. Изменяя величину частоты ЭДС, следите за перемещением отметки на резонансной кривой и числовым значением добротности (U_0C/₀). Добейтесь максимального значения добротности и соответствующие значения частоты источника ЭДС и собственной частоты контура занесите в табл. 1. Повторите измерения для других значений емкости конденсатора из табл. 1.
   
4. 
   Повторите измерения для двух других значений индуктивности катушки, выбирая их из табл. 2. Полученные результаты запишите в табл. 3 и 4.
   

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА

1. 
   Постройте на одном листе графики зависимости резонансной частоты от корня из обратной емкости при трех значениях индуктивности.
   
2. 
   Для каждой прямой определите котангенс угла наклона по формуле
   

ctg =  A_ЭКСП.

3. 
   Вычислите теоретическое значение константы А_ТЕОР для каждой прямой по формуле А_ТЕОР = .
   
4. 
   Заполните таблицу результатов измерений.
   

Номер измерения	АЭКСП, Гн1/2	АТЕОР, Гн1/2

Сделайте выводы по графикам и результатам измерений.

Вопросы и задания для самоконтроля

1. 
   Что такое колебательный контур?
   
2. 
   Каковы электрические характеристики резистора, конденсатора, катушки?
   
3. 
   Дайте определение гармонических колебаний.
   
4. 
   Что такое период колебания?
   
5. 
   Какая физическая величина испытывает колебания в колебательном контуре?
   
6. 
   Напишите формулу для напряжения на конденсаторе.
   
7. 
   Напишите формулу для напряжения на катушке индуктивности. Какое другое название она имеет?
   
8. 
   Напишите формулу для напряжения на резисторе. Какое другое название она имеет?
   
9. 
   Какие законы выполняются для тока и напряжения на отдельных элементах в колебательном контуре?
   
10. 
    Сформулируйте и запишите в виде формулы закон электромагнитной индукции в общем виде.
    
11. 
    Сформулируйте и запишите в виде формулы закон электромагнитной индукции для проводящего контура.
    
12. 
    Сформулируйте и запишите в виде формулы закон самоиндукции.
    
13. 
    Запишите дифференциальное уравнение для заряда на конденсаторе в контуре, где существуют свободные гармонические колебания.
    
14. 
    Запишите дифференциальное уравнение для заряда на конденсаторе в контуре, где существуют свободные затухающие колебания.
    
15. 
    Напишите формулу циклической частоты свободных гармонических колебаний в контуре.
    
16. 
    Напишите формулу зависимости заряда на конденсаторе от времени при свободных гармонических колебаниях в контуре.
    
17. 
    Напишите формулу циклической частоты свободных затухающих колебаний в контуре.
    
18. 
    Напишите формулу зависимости заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре.
    
19. 
    Напишите формулу для коэффициента затухания.
    
20. 
    Дайте определение постоянной времени затухания.
    
21. 
    Напишите формулу логарифмического декремента затухания. Что он характеризует?
    
22. 
    Напишите формулу связи логарифмического декремента затухания с коэффициентом затухания.
    
23. 
    Напишите формулу для добротности контура. Что определяет добротность?
    
24. 
    Нарисуйте зависимость заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре. Покажите на рисунке, как определяется графически постоянная времени затухания.
    
25. 
    Дайте определение вынужденным колебаниям.
    
26. 
    Что такое колебательный контур?
    
27. 
    Когда возникают вынужденные гармонические колебания?
    
28. 
    Как графически изображается комплексная величина?
    
29. 
    Что такое комплексная амплитуда тока или напряжения?
    
30. 
    Дайте определение импеданса.
    
31. 
    Что такое полное электрическое сопротивление?
    
32. 
    Чему равен импеданс резистора?
    
33. 
    Чему равен импеданс идеальной катушки индуктивности?
    
34. 
    Как формулируется закон электромагнитной индукции для катушки?
    
35. 
    Чему равен импеданс конденсатора?
    
36. 
    Чему равны реактивные сопротивления катушки и конденсатора?
    
37. 
    Чему равно реактивное сопротивление последовательно соединенных катушки и конденсатора?
    
38. 
    Чему равен импеданс колебательного контура?
    
39. 
    Чему равен полное сопротивление колебательного контура?
    
40. 
    Дайте определение резонанса для тока в колебательном контуре.
    
41. 
    На какой частоте наблюдается резонанс для тока в колебательном контуре?
    
42. 
    На какой частоте наблюдается резонанс для напряжения на конденсаторе в колебательном контуре?
    
43. 
    Чему равно отношение амплитуд напряжения на конденсаторе при резонансе и ЭДС?
    
44. 
    Чему равно характеристическое сопротивление контура? Как оно влияет на добротность?
    
45. 
    Что такое резонансная кривая контура?
    

(Подробное изложение теории можно найти в курсе общей физики И. В. Савельева, т. 2, 1970, § 92–101. В последующих изданиях отсутствует).