Лабораторная работа 302 исследование явления дисперсии

• Название: Лабораторная работа 302 исследование явления дисперсии
• Дата: 20.04.2022
• Размер: 466 Kb.
• Имя файла: 302_0.doc
• Тип: Лабораторная работа; #486937

Лабораторная работа №3-02
ИССЛЕДОВАНИЕ ЯВЛЕНИЯ ДИСПЕРСИИ
Цель работы: сформулировать гипотезу исследования, выделить уровни сложности изучаемой системы, исследовать явление дисперсии света с помощью дисперсионной призмы.

Приборы и принадлежности: источник света (ртутная лампа), гониометр Г5, дисперсионная призма.
Краткое теоретическое введение
Дисперсия света в прозрачных материалах, применяемых в оптичес­ких устройствах, играет важную роль при расчете элементов спектраль­ных приборов, при расчете ахроматичности линз или призм, при оценке хроматической аберрации линз.

Во многих спектральных приборах – монохроматорах, спектрографах, спектрофотометрах и т.п. в качестве диспергирующих элементов исполь­зуются спектральные призмы, действие которых основано на явлениях преломления и дисперсии света (дисперсионные призмы). Именно призма определяет основные характеристики этих приборов – угловую дисперсию и разрешающую способность.

Явление дисперсии света представляет собой зависимость показателя преломления n вещества от длины  (или частоты ) световой волны падающего света. Дисперсия характерна для всех веществ. Первые экспериментальные исследования указанной зависимости были проведены И. Ньютоном (в 1672 г.), который пропускал пучок белого света через призму, помещенную в воздухе, и на экране, установленном за призмой, наблюдал спектр.

Согласно классической теории дисперсии, разработанной на основе электромагнитной теории света и электронной теории вещества, явление дисперсии объясняется взаимодействием световых волн с электронами атомов среды. Движение электронов в атоме подчиняется законам квантовой механики, в частности, понятие траектории электрона в атоме теряет всякий смысл. Однако, как показал Лоренц, для качественного понимания многих оптических явлений можно ограничиться гипотезой о существовании в атомах вещества электронов, которые удерживаются около своих положений равновесия квазиупругими силами и совершают гармонические колебания с собственной частотой ₀. Падающая световая волна вызывает вынужденные колебания электронов со своей частотой . Будучи выведенными из положения равновесия, такие электроны колеблются, постепенно теряя энергию колебания на излучение электромагнитных волн. Таким образом, каждая частица излучает вторичные волны. Вторичная волна, складываясь с первичной, образует результирующую волну с амплитудой и частотой, отличной от амплитуды и частоты первичной волны, и, следовательно, изменяется скорость световой волны v в среде (v =  / k, где k – волновое число). Абсолютный показатель преломления вещества n связан со скоростью света в среде следующим соотношением:

(1)

где с – скорость света в вакууме.

Таким образом, световые волны с разной частотой  (т.е. разной длиной волны  = 2с/) имеют в среде разные скорости v и, следовательно, в соответствии с соотношением (1) показатель преломления n данного вещества будет зависеть от длины волны падающего монохроматического света. Белый свет будет разлагаться в спектр. Указанную зависимость можно охарактеризовать функцией

n = f (₀), (2)

где ₀ – длина световой волны в вакууме.

Если вещество поглощает часть лучей, то в областях частот, соответствующих полосам интенсивного поглощения света веществом и вблизи них наблюдается аномальная дисперсионная зависимость. Нормальная и аномальная дисперсионные зависимости отличаются знаком величины (или ); для нормальной дисперсии .

На явлении нормальной дисперсии основано действие призменных спектрографов и спектроскопов. В соответствии с зависимостью (2) свет разных длин волн отклоняется дисперсионной призмой на разные углы, т.е. образуется спектр. Если излучение источника света содержит набор монохроматических лучей различных длин волн ₁, ₂, ₃, …, то спектр будет состоять из отдельных спектральных линий конечной ширины. Ширина спектральной линии определяется дифракцией света на оправе призмы (или на краях диафрагмы, ограничивающей световой поток, падающий на призму).

Качество спектра определяется угловой дисперсией и разрешающей способностью призмы.

Угловая дисперсия D определяет угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на 1 Å, т.е.

(3)

где d – угловое расстояние между спектральными линиями, отличающимися по длине волны на d.

Величина D выражается в рад / Å.

Способность призмы разделять близкие спектральные линии ₁ и ₂ определяется не только угловым расстоянием d между ними, но и шириной 2 спектральной линии (рис. 1). Если спектральные линии размыты и имеют значительную ширину, то даже при сравнительно большом угловом расстоянии между ними результирующая картина, возникающая от их наложения, не позволяет воспринимать эти линии раздельно.

С ледовательно, чем уже спектральные линии, тем более близкие линии можно увидеть раздельно. Эту характеристику призмы называют разрешающей способностью. За меру разрешающей способности принимают величину

(4)

где d – наименьшая разность длин волн двух еще видимых раздельно линий;  – длина волны спектральной линии, вблизи которой производят измерение.

Величину d определяют из критерия Релея, согласно которому две близкие спектральные линии считаются разрешенными, если максимум одной из них совпадает с минимумом другой (рис. 1, б)

d = . (5)

И сследовать дисперсионные призмы можно путем определения показателя преломления для различных длин волн по измерению углов отклонения световых лучей призмой. Углом отклонения  называется угол между направлением падающего на призму луча и направлением луча, вышедшего из призмы (рис. 2). Этот угол  зависит от угла падения i лучей на призму, от преломляющего угла призмы  и от показателя преломления n вещества призмы, который сам является величиной, зависящей от длины световой волны . Причем наиболее удобно наблюдать дисперсионный спектр и делать измерения для призмы, когда она установлена вблизи угла наименьшего отклонения _min в параллельных лучах света. Угол _min функционально связан с показателем преломления n вещества призмы и будет различным для различных длин волн. По результатам измерений может быть построена искомая дисперсионная зависимость (2) и определены характеристики призмы (3) и (4).

Методика постановки данного исследования определяется с учетом расчетных соотношений для искомых физических величин: n, D, R. Найдем выражение, позволяющее определять показатель преломления вещества призмы по результатам измерения других физических величин (углов) при выбранном методе исследования.

Рассмотрим ход луча, проходящего через трехгранную призму (рис. 2), луч света дважды испытывает преломление (на гранях призмы AE и AF) и отклоняется к основанию призмы EF в соответствии с законами преломления.  – преломляющий угол призмы. Угол отклонения луча  на рис. 2 образован пересечением в точке М луча, падающего на призму, с продолжением луча, вышедшего из призмы, i и r – углы падения и преломления на преломляющей поверхности AE; r₁ и i₁ – углы падения и преломления на поверхности AF.

На основании закона преломления

,

где n – показатель преломления вещества призмы; n_возд = 1 – показатель преломления окружающей среды (воздуха). Тогда

sin i = n sin r. (6)

Нормали к преломляющим боковым граням призмы, проведенные через точки С и B, пересекаются в точке D. В треугольнике СDВ угол СDВ является дополнительным для угла . В то же время этот угол СDВ является дополнительным для суммы углов r + r₁ (СDВ + r + r₁ = 180 °), т.е.  = r + r₁.

Угол  является внешним углом треугольника СМВ, поэтому

 = МСВ + МВС = (i – r) + (i₁ – r₁) = i + i₁ – .

Для определения показателя преломления призмы берут обычно тот случай, когда луч внутри призмы идет параллельно ее основанию (рис. 2). При этом угол  имеет наименьшее из всех возможных значений (_min), поэтому такое положение призмы относительно падающего луча называется положением наименьшего отклонения, о котором говорилось выше. В этом случае

i=i₁, r=r₁, =2i – 

или

(7)

Подставляя данные значения (7) в уравнение (6), получим

(8)

Таким образом, в данной работе в соответствии с (8) показатель преломления вещества призмы определяется по результатам измерений углов  и _min.

Задачей данного исследования является также определение характеристик призмы D (3) и R (4). Выражение для угловой дисперсии призмы D можно получить, дифференцируя выражение (8) по . Произведя незначительные преобразования с учетом (7), находим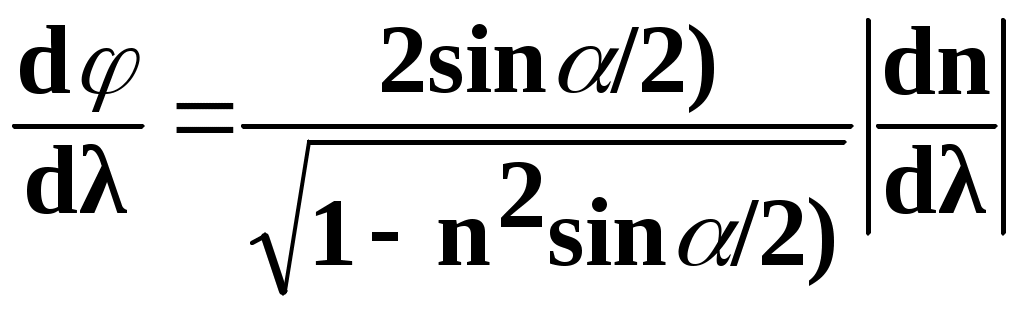

, (9)

где dn/d  дисперсия вещества призмы.

Если преломляющий угол призмы  = 60°, то выражение (9) перепишется в виде

. (10)

Разрешающая способность призмы определяется согласно выражению (4). Используя равенство (5), можно получить следующее соотношение:

(11)

г де (a – b) – разность путей, проходимых в призме крайними лучами (рис. 3).

Для максимального использования разрешающей способности необходимо, чтобы световой пучок покрывал всю боковую поверхность призмы. В этом случае b = 0, а = l (l – основание призмы), тогда

(12)

Используя дисперсионную зависимость, можно определить показатель преломления вещества призмы для различных длин волн (спектральных линий) любого источника. Проводя эксперименты с призмами, выполненными из различных материалов, можно провести сравнительные исследования характеристик различных дисперсионных призм.

Методика и техника измерений

Описание конструкции гониометра
Гониометр – прибор, предназначенный для точных измерений углов оптическим методом. Внешний вид гониометра представлен на рис. 4 а, б.

Он состоит из коллиматора 4, зрительной трубы 9, столика 24, на котором располагается изучаемый объект, отсчетного микроскопа и лимба, скрытого в корпусе. Лимб, столик и корпус прибора могут вращаться вокруг вертикальной оси.

Коллиматор служит для создания параллельного пучка света. Он представляет собой трубу, на одном конце которой имеется объектив, на другом – узкая щель 2, расположенная в фокальной плоскости объектива. Ширину щели можно регулировать с помощью микрометрического винта. Для фокусировки объектива коллиматора служит винт 5. Наклон коллиматора в вертикальной плоскости можно изменять с помощью юстировочного винта 6.



1– стойка коллиматора; 2 – раздвижная щель; 3 – кольцо; 4 – коллиматор; 5 – маховичок фокусировки коллиматора; 6 – юстировочный винт; 7 – винт наклона столика; 8 – шкала; 9 – зрительная труба; 10, 11 – рычажки; 12 – алидада; 13 – механизм соединения лимбы с алидадой; 14 – маховичок; 15 – общий выключатель; 17 – внутри алидады подсветка лимба; 18 – основание; 19 – маховичок отсчетного микроскопа; 20 – автоколлимационный окуляр-куб; 21 – кольцо; 22 – маховичок фокусировки трубы; 23 – юстировочный винт; 24 – столик; 28 – микрометрический винт лимба; 29 – стопорный винт алидады; 30 – подъемный винт; 31 – микрометрический винт алидады.

Зрительная труба состоит из объектива и окуляра, с помощью которого рассматривается изображение, полученное в фокальной плоскости объектива. 23 – юстировочный винт для зрительной трубы. 22 – фокусирующий винт. Зрительная труба укреплена на кронштейне-алидаде 12, которую можно поворачивать вокруг вертикальной оси, проходящей через центр п
редметного столика. Поворот трубы осуществляется от руки после освобождения зажимного винта 29. При закреплении винта 29 можно производить тонкое перемещение трубы винтом 31. Рычажки 10 и 11 позволяют производить совместное или раздельное перемещение трубы и лимба. Для совместного перемещения этот рычажок надо опустить. Стопорный винт служит для закрепления лимба, при этом винтом 28 можно осуществлять тонкое перемещение лимба. Винты 7 и 26 служат для наклона столика.

Таким образом, столик может вращаться самостоятельно совместно с лимбом при неподвижной зрительной трубе и, наконец, совместно с лимбом и трубой.

Лимб гониометра снабжен шкалой с делениями. Отсчет делений по лимбу производится с помощью отсчетного микроскопа с ценой деления 1. Для это
го надо повернуть маховичок 19 настолько, чтобы верхние и нижние двойные штрихи лимба в левой части окна отсчетного микроскопа совместились, как показано на рис. 5. Число градусов будет равно ближайшей цифре, видимой слева от вертикального индекса верхней шкалы. Число десятков минут – числу интервалов, заключенных между верхним штрихом, соответствующим отсчитанному числу градусов, и нижним оцифрованным штрихом, расположенным справа от вертикального индекса. Число единиц отсчитывается по шкале, расположенной в правой части окна поля зрения по левому ряду чисел вертикальной шкалы. Число секунд – в том же окне по правому ряду чисел с помощью неподвижного горизонтального индекса. Положение, показанное на рис. 5, соответствует отсчету 01557. Окуляр зрительной трубы снабжен автоколлимационным устройством, позволяющим установить ось зрительной трубы строго перпендикулярно к интересующей нас плоскости, например к плоскости решетки. Принцип действия этого устройства показан на рис. 6.

Лампочка 5 (см. рис. 6) освещает прозрачный крест на пластине 6. Прошедшие через него лучи отражаются от диагональной грани стеклянного кубика 7, проходят через объектив 8 зрительной трубы 4 и, отразившись от некоторой плоской поверхности, например от дифракционной решетки 3, возвращаются в трубу, образуя в фокальной плоскости 9 объектива изображение светлого креста. Если плоскость поверхности перпендикулярна к оси трубы, то изображение этого креста совместится с визирным крестом, расположенным в плоскости 9.

Н
а рис. 6 обозначено: 1 – источник света; 2 – коллиматор; 3 – призма; 4 – зрительная труба; 5, 6, 7 – автоколлимационное устройство; 8 – объектив зрительной трубы; 9 – фокальная плоскость объектива.
Методика измерений

1. Определение преломляющего угла призмы

П ризма устанавливается на столик гониометра так, что параллельный пучок лучей падает перпендикулярно ее матовой грани а (рис. 7).

Луч I отражается от левой грани призмы, луч II – от правой. Сумма углов около точки D составляет 360°, т.е.

4 +  =  360. (13)

Из треугольника МDN видно, что

 = 90   ( / 2). (14)

Подставляя (14) в (13), получим 4 (90   ( / 2)) +  = 360 .

Отсюда

 =  / 2. (15)

Таким образом, преломляющий угол призмы  можно опытно определить, если измерить угол , на который нужно поместить ось зрительной трубы, чтобы сначала увидеть изображение щели коллиматора, которое дают лучи, отразившиеся от правой грани призмы (₁), а затем от левой (₂)

 = |₁ – ₂|. (16)
2 . Определение угла наименьшего отклонения

Призма устанавливается на столике гониометра так, чтобы в поле зрения трубы появился линейчатый спектр (рис. 8). Наблюдая за спектром через окуляр зрительной трубы, необходимо поворачивать столик гониометра с призмой так, чтобы угол падения i уменьшался, при этом уменьшается и угол  (рис. 2). Для того чтобы спектр оставался в поле зрения, необходимо поворачивать соответственно и зрительную трубу. Момент остановки спектра (т.е. тот момент, когда спектр останавливается, а при дальнейшем повороте столика с призмой начинает двигаться в противоположную сторону) соответствует наименьшему значению угла отклонения (при дальнейшем повороте он будет увеличиваться).

В момент остановки спектра производится отсчет углов для всех линий спектра для правой грани призмы (₁, ₂, …) (рис. 8) и для левой грани призмы (₁, ₂, …). Угол наименьшего отклонения для каждой i-й линии спектра равен

(17)

где _min i и _min i – углы наименьшего отклонения для i-й линии спектра, определяемые, соответственно, для правой и левой граней призмы

_mini = |_i   ₀ |. (18)

Здесь ₀ – угол, определяющий положение изображения щели в отсутствии призмы; знак «+» или «–» определяется положением отсчета _i относительно отсчета ₀ (если для одной из граней берется знак «+», то для другой – «–»).

По результатам измерений _min для всех линий спектра и  согласно (8) определяются значения n для различных линий данного спектра. Используя результаты вычислений и данные табл. 1 (если в качестве источника света используется ртутная лампа), строится зависимость n = f(₀).

Таблица 1

Цвет линий спектра паров ртути	Яркость линий	, нм
Красная	Яркая	670
Оранжевая	Очень слабая	612
Желтая	Яркая	579
Желто-зеленая	Яркая	538
Голубая	Яркая	436
Фиолетовая	Яркая	405

Методика и техника измерений

А. Измерение преломляющего угла  призмы

1. Поместите источник света перед щелью коллиматора гониометра (ртутную лампу).

2. Добейтесь резкого изображения щели, передвигая окуляр вдоль оси зрительной трубы, Для этого необходимо установить зрительную трубу так, чтобы ее визирная нить оказалась на середине изображения щели.

3. Произведите отсчет ₀ (не менее 3 раз) по лимбу, фиксируя положения зрительной трубы. В табл. 3 заносится значение _0ср.

3. На столик гониометра поместите призму, обратив ее матовую поверхность к объективу зрительной трубы, и установите ее параллельно плоскости выходного отверстия коллиматора. Выходящий из коллиматора пучок света должен разделиться на два пучка, один из которых падает на левую, а другой – на правую грань призмы (рис. 7).

4. Глядя в окуляр, переместите зрительную трубу, например, вправо до тех пор, пока ее вертикальная нить не совместится с серединой правого изображения щели; показание ₁, отсчитанное по лимбу, запишите в табл. 2.

5. Переместите трубу в противоположном направлении (влево) до тех пор, пока вертикальная нить не совместится с серединой левого изображения щели, отсчет ₂ занесите в табл. 2.

6. Вычислите значение угла  = |₁ – ₂|.

7. Опыт проведите не менее трех раз и определите _ср.

8. По значению _ср найдите величину преломляющего угла призмы. Все данные занесите в табл. 2.

Таблица 2

№ опыта	Положение трубы
	1	2		ср	

Таблица 3

Рабочая грань призмы	0ср	Цвет линии спектра	, нм	№ опыта	Положение трубы i	iср	min i	min
Правая
Левая

В. Измерение углов наименьшего отклонения

1. Поворачивая столик гониометра, установите призму так, чтобы лучи из коллиматора падали на одну из преломляющих граней призмы (рис. 8). В поле зрения трубы, при соответствующем ее положении, появится линейчатый спектр.

2. Глядя в окуляр, медленно вращайте столик, а за ним и зрительную трубу в направлении, при котором угол падения лучей на грань призмы уменьшается. При этом будет уменьшаться и угол отклонения , поэтому если замедлить вращение трубы, то при продолжении вращения столика спектр уйдет из поля зрения. Пока угол  не достиг своего минимального значения, вращать трубу приходится вслед за столиком. После того, как угол отклонения лучей достиг своего минимального значения _min, при дальнейшем уменьшении угла падения лучей на грань призмы (что происходит, если продолжать вращение столика в прежнем направлении), спектр сначала останавливается, а затем начинает перемещаться в направлении, противоположном первоначальному. Это значит, что угол отклонения лучей призмой снова начал увеличиваться.

Чтобы определить угол наименьшего отклонения лучей, нужно уловить момент остановки спектра и в этот момент прекратить совместное вращение столика и зрительной трубы. Оставляя столик с призмой неподвижными, поворачивайте зрительную трубу, поочередно совмещая ее нить с серединой каждой цветной линии спектра, и определите соответствующее деление лимба _i при данном положении трубы. Значение _i записывают в табл. 3. Опыт произведите не менее 3 раз и определите _iср для каждой из наблюдаемых спектральных линий.

3. Поворачивая столик гониометра, найдите спектр, образовавшийся при преломлении световых лучей на другой грани призмы (если сначала преломление лучей происходило на правой грани, то теперь оно должно происходить на левой грани). Аналогично описанному в п. 2 определите для каждой из наблюдаемых линий спектра, и данные запишите в табл. 3.

4. По формуле (18) определите значения _min i и _min i, используя _0ср и _iср:

_min i = | _iср – _0ср|,

и данные запишите в табл. 3.

5. Определите значения углов наименьшего отклонения и эти значения запишите в табл. 3

.
С. Обработка результатов измерений

1. Используя формулу (8) и данные табл. 3 и 1, вычислите показатель преломления n для всех наблюдаемых длин волн источника света (имеющиеся в лаборатории источники света дают не все указанные в таблицах линии).

2. По данным табл. 3 и 1 постройте дисперсионную кривую n = f(₀).

3. Из графика определите дисперсию n /  вещества для коротковолнового и длинноволнового участков спектра.

4. Используя формулы (9), или (10), или (12), определите дисперсию D и разрешающую способность призмы (в зависимости от используемой призмы и условий эксперимента). При использовании (12) ширина светового пучка (a – b) должна быть известна.

5. Вычислите абсолютную и относительную погрешности.

Вопросы и задания для самостоятельной работы
1. Выделите два уровня сложности по изучению явления дисперсии света. Какова схема наблюдения дисперсии света?

2. Чем отличаются дисперсия нормальная и дисперсия аномальная?

3. Приведите графическое изображение функции, характеризующей явление дисперсии для всех прозрачных бесцветных веществ в видимой части спектра.

4. Изобразите дисперсионную зависимость для веществ, поглощающих часть падающих на них лучей, в области полосы поглощения.

5. Как зависит скорость световых волн в диспергирующих средах от частоты  (или от длины волны ₀) падающего излучения?

6. Дайте определение групповой и фазовой скорости волн. Как соотносится групповая и фазовая скорости для нормальной дисперсии? В каком случае групповая и фазовая скорости равны?

7. Как групповая скорость соотносится с дисперсией вещества?

8. Какая фундаментальная теория положена в основу классической теории дисперсии?

9. Почему фазовая скорость распространения волны может быть больше скорости света?

10. Объясните, почему все экспериментальные методы определения скорости света дают значение групповой скорости, а не фазовой.

11. Какую величину принято называть средней дисперсией вещества в диапазоне длин волн от ₁ до ₂?

12. Какую величину называют дисперсией вещества для данной длины волны?

13. Почему аномальная дисперсия наблюдается в области поглощения и вблизи от нее? Как экспериментально обнаружить область аномальной дисперсии света?

14. Решите следующую задачу: Показатель преломления прозрачного вещества для небольшого интервала длин волн, вдали от линий поглощения, связан с длиной волны соотношением n = А + В/₂. (А и В – размерные константы). Определите: а) дисперсию вещества; б) фазовую скорость; в) групповую скорость.

15. Почему достаточно узкий световой пучок дает спектр после прохождения призмы, а у широкого пучка окрашенными оказываются только края?

16. Укажите существенные различия между спектрами, полученными с помощью дифракционной решетки и с помощью призмы.

17. Приведите пример и опишите какое-либо природное явление дисперсии.

18. Для большинства газов, например для воздуха, водорода, гелия и т.д., собственные частоты колебаний электронов соответствуют ультрафиолетовому свету. Как это сказывается на значении показателя преломления?

19. Объясните, каким образом нужно устанавливать призму под углом наименьшего отклонения?

20. Укажите основные части используемого в работе для измерения углов гониометра, а также объясните, какая часть гониометра при проведении измерений все время остается неподвижной.

21. Покажите ход лучей в призме, используемой в работе, и все характерные углы.

22. Приведите формулу для определения показателя преломления вещества призмы.

23. Что называется угловой дисперсией и разрешающей способностью призмы? Как определяются эти величины?

24. Получите формулу, позволяющую оценить погрешность в определении показателя преломления призмы для некоторой длины волны .

25. Что можно сказать о линейной дисперсии призмы n/ по результатам измерений? Как изменяется линейная дисперсия призмы на различных участках спектра?