Лаба 7.1 инфа 1 курс. лаба7.1 БИК2109 Малевич Татьяна. Лабораторная работа 7 Проект 1 Разработка проекта, решающего задачу принадлежности или непринадлежности точки с заданными координатами геометрической фигуре
 Скачать 223.53 Kb.
|
|
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики»  Кафедра «Информатика»Лабораторная работа №7 - Проект 1 «Разработка проекта, решающего задачу принадлежности или непринадлежности точки с заданными координатами геометрической фигуре» по теме: «Логические данные и выражения. Операторы разветвления VС++. Программная реализация базовых разветвляющиеся структур и типовых алгоритмов». Выполнил: студент гр. БИК2109 Малевич Т.Ф. Вариант №14 Проверил: старший преподаватель Загвоздкина А.В. Москва, 2021 г. 1)Индивидуальное задание 2  )Формализация задания Задание состоит в том, чтобы для выделенной области определить и записать логическое выражение с условием, зависимое от двух переменных x и y (где [x,y] координаты точки), принимающее логическое значение false (0) или true (1), в зависимости от попадания или не попадания точки с координатами X, Y в выделенную область рисунка. Строим график своего индивидуального задания (рис. 1): Р 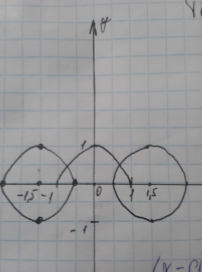 исунок 1- график индивидуального задания Далее запишем условие. Если точка попадает в одну из окружностей или же попадают в дугу, то условие выполняется. Условие является таким: (x+1.5)^2+(y+0)^2<= 1 | | (x-1.5)^2+(y+0)^2<=1 | | y=(1 – x^2)^½ Для C++ это выражение будет записываться так: ((x+1.5)*(x+1.5)+(y*y))<= 1 | | ((x-1.5)*(x-1.5)+(y*y))<=1 | | y= =sqrt(1 – x*x) 3) Схемы алгоритмов Я разработала схемы 3-х алгоритмов. Схема алгоритма Resh1 решения задачи, использующая стандартное разветвление и сложное логическое выражение (рис. 3.1): Р 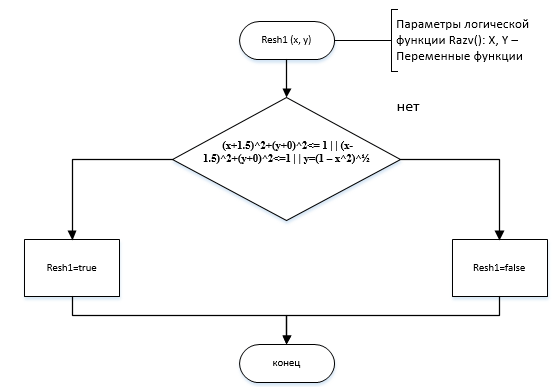 исунок 3.1 - схема алгоритма Resh1 Схема алгоритма Resh2 решения задачи, использующая вложенные разветвления только с помощью операций отношения, без использования логических операций и сложных логических выражений (рис. 3.2): Поправка: в комментарии вместо razv() должен быть razv2(), заметила во время проверки задания перед отправкой. Р 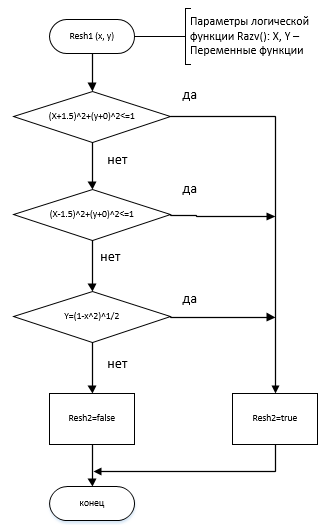 исунок 3.2 - схема алгоритма Resh2 Схема алгоритма Resh3 решения задачи, использующая только сложное логические выражения(рис. 3.3): Р 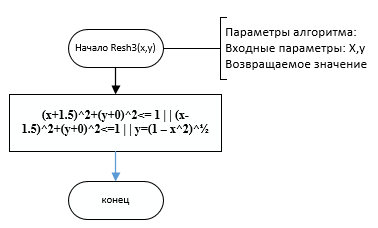 исунок 3.3 - схема алгоритма Resh3 4)Разработка программного проекта Далее разрабатываем программный код проекта для решения задания.  #include bool Resh1(float x, float y) { if (((x-1.5)*(x-1.5)+(y*y))<= 1 || ((x+1.5)*(x+1.5)+(y*y))<=1 || y==sqrt(1-x*x)) return true; else return false; } bool Resh2(float x, float y) { if ((x-1.5)*(x-1.5)+(y*y) <= 1) return true; if ((x+1.5)*(x+1.5)+(y*y) <= 1) return true; if (y==(sqrt(1-x*x))) return true; return false; } bool Resh3(float x, float y) { return (((x-1.5)*(x-1.5)+(y*y))<= 1 || ((x+1.5)*(x+1.5)+(y*y))<=1 || y==sqrt(1-x*x)); } Рисунок 5 - файл с функциями решения  #include using namespace std; void GetXY(float&x, float&y) { setlocale(0, ""); cout<<"Введите координаты точек x, y\n "; cin>>x>>y; } void Put(bool b, float x, float y) { setlocale(0, ""); cout<<"Точка с координатами( "< if (b) cout<<"Попала в заданную область"< else cout<<"Не попала в заданную область"< } Рисунок 6 - файл с функциями ввода и вывода Файл с главной функцией main (рис. 4.3).  using namespace std; void GetXY(float&x, float&y); void Put(bool b, float x, float y); bool Resh1(float x, float y); bool Resh2(float x, float y); bool Resh3(float x, float y); int main() { float x, y; bool b, c, d; GetXY(x,y); cout<<"Решение 1-й функции:"< b=Resh1(x,y); Put(b,x,y); cout<<"Решение 2-й функции:"< c=Resh2(x,y); Put(c,x,y); cout<<"Решение 3-й функции:"< d=Resh3(x,y); Put(d,x,y); system("Pause"); return 0; system("Pause"); return 0; } Рисунок 7 - файл главной функции main 5) Результат работы программы Проверяем программу на числах, попадающих в заданную точку (рис.5.1): 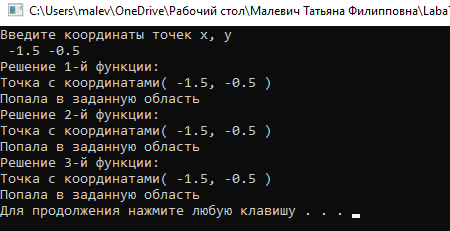 Рисунок 5.1-Результат работы программы с тестовыми числами, попадающими в заданную точку Проверим работу программы на других числах, не попадающих в очки(рис.5.2: Р 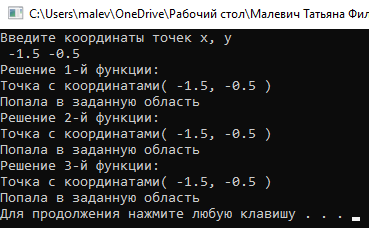 исунок 5.2 -Результат работы программы с тестовыми числами, попадающими в заданную точку 6) Доказательство правильности результата Разработаны с тестовые исходные данные для контрольного решения, проверяющие попадание и непопадание точки с различными координатами в заданную область, и получены результаты: П  ри тестовых данных результаты ручного расчета и вычисления на компьютере совпадают. |