Лабораторная работа 9 Построение модели тренда с учетом автокорреляции остатков ст группы сл120 Цюань Т

• Название: Лабораторная работа 9 Построение модели тренда с учетом автокорреляции остатков ст группы сл120 Цюань Т
• Дата: 14.12.2022
• Размер: 21.46 Kb.
• Имя файла: Lb9.docx
• Тип: Лабораторная работа; #845349

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Владимирский Государственный Университет им А.Г. и Н.Г. Столетовых» (ВлГУ)

Гуманитарный институт

Кафедра социологии

Лабораторная работа №9

«Построение модели тренда с учетом автокорреляции остатков»

Выполнил:

ст. группы СЛ-120

Цюань Т.

Проверил:

к.ф-м.н.

Курбыко И.Ф.

Владимир

2022

Исходные данные

Y_t –денежные доходы в среднем на душу населения в конце декабря, рублей

t – условное время

Год	t	y(t)
2000	1	1658.9
2001	2	2281.1
2002	3	3062
2003	4	3947.2
2004	5	5167.4
2005	6	6399
2006	7	8088.3
2007	8	10154.8
2008	9	12540.2
2009	10	14863.6
2010	11	16895
2011	12	18958.4
2012	13	20780
2013	14	23221.1
2014	15	25684
2015	16	27412
2016	17	30254
2017	18	30865
2018	19	31745
2019	20	33010
Среднее	10.5	16349.35

Задание:

Уравнение линейной модели тренда следующее: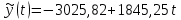



Задание:

1. 
   Используя ряд остатков по линейной модели тренда, найти коэффициент автокорреляции первого порядка ряда остатков.
   
2. 
   Построить уравнение новой линейной модели тренда, используя автокорреляцию остатков.
   
3. 
   Найти ряд остатков по новой модели тренда и вычислить стандартную ошибку модели, а также среднюю относительную ошибку аппроксимации исходных данных.
   
4. 
   Сравнить стандартную ошибку и среднюю относительную ошибку по новой модели с ошибками по начальной линейной модели (см. работу №6).
   
5. 
   Построить прогноз показателя на шаг вперед по новой модели и вычислить соответствующий доверительный интервал прогноза.
   
6. 
   Сравнить результаты прогнозирования по новой модели с прогнозом по первоначальной модели (см. работы №6-8).
   

1. 
   Коэффициент автокорреляции первого порядка ряда остатков равен:
   

r(1)=0,83158

2. 
   Уравнение новой линейной модели тренда, используя автокорреляцию остатков: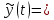
   

-3025,82+1845,25t +0,83158*e(t-1), t=1,2,…,19,20

3. 
   Ряд остатков по новой модели тренда и стандартная ошибка модели, а также средняя относительная ошибка аппроксимации исходных данных равны:
   

Se=	1241,669
Se1=	616,2447
Еотн%=	11,58048
Еотн1%=	7,098543

4. 
   Расчёт ошибок по линейной модели тренда и модели с учетом автокорреляции остатков предыдущей модели показал, что новая модель точнее описывает исходные данные
   

5. 
   Построим прогноз показателя на шаг вперед по новой модели и вычислим соответствующий доверительный интервал прогноза.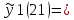
   

-3025,82+1845,25*21+0.83158*e(21)= 35001,57197

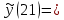-3025,82+1845,25*21= 37664,41913

(32338,72482; 37664,41913)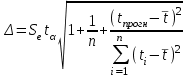



С учетом новой стандартной ошибки Se1= 616,2447 вычислим доверительный интервал прогноза на 2021 год по новой модели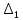

= 2662,847156
Имеем доверительный интервал: (32858.90799; 38589.95833)

Длина нового доверительного интервала составляет 5325,694312

Длина старого доверительного интервала составляет 5731,050344

Таким образом, новая модель меньше по сравнению с первоначальной модели.