Контрольная работа по эконометрики вариант №8. Задача 1 3 Ситуационная (практическая) задача 2 25 Тестовые задания 32 Список использованной литературы 35
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
Титульный лист Эконометрика Вариант 8 Содержание Ситуационная (практическая) задача № 1 3 Ситуационная (практическая) задача № 2 25 Тестовые задания 32 Список использованной литературы 35 Ситуационная (практическая) задача № 1По 25 регионам РФ имеются данные о потребительских расходах в среднем на душу населения, руб., среднедушевых денежных доходах населения, в месяц, тыс. руб., уровне безработицы, % (по данным выборочных обследований рабочей силы; в среднем за год; население в возрасте 15-72 лет) за 2018 год: Таблица 1 Результаты обследования регионов
Требуется: 1. Построить корреляционное поле между потребительскими расходами в среднем на душу населения, тыс. руб. и среднедушевыми денежными доходами населения в месяц, тыс. руб. Выдвинуть гипотезу о тесноте и виде зависимости между потребительскими расходами и среднедушевыми денежными доходами. 2. Оценить тесноту линейной связи между потребительскими расходами и среднедушевыми денежными доходами с надежностью 0,9. 3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости потребительских расходов в среднем на душу населения от среднедушевых денежных доходов населения. Дать содержательную интерпретацию параметров уравнения. 4. Дать интервальные оценки для параметров модели парной регрессии с доверительной вероятностью γ = 0,9. 5. Проверить статистическую значимость параметров уравнения парной регрессии с надежностью γ = 0,9. 6. Проверить качество построенного уравнения регрессии с помощью средней ошибки аппроксимации и с помощью коэффициента детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью γ = 0,9. 6. Для домохозяйства с среднедушевыми денежными доходами населения в месяц 62,5 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,9. 7. Дать точечный и интервальный прогноз потребительских расходов в среднем на душу населения с надежностью γ = 0,9 для гипотетического региона, в котором среднедушевые денежные доходы населения в месяц на 3% больше среднего по выборке. 8. Рассчитать коэффициенты линейного уравнения множественной регрессии для зависимости потребительских расходов в среднем на душу населения от среднедушевых денежных доходов населения и уровня безработицы. Пояснить экономический смысл его параметров. 9. Дать интервальные оценки для параметров модели множественной регрессии с доверительной вероятностью γ = 0,9. 10. Проверить статистическую значимость параметров уравнения множественной регрессии с надежностью γ = 0,9. 11. Проверить качество построенного уравнения регрессии с помощью коэффициента детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью γ = 0,9. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 12. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты. 13. Дать точечный и интервальный прогноз потребительских расходов в среднем на душу населения с надежностью γ = 0,9 для гипотетического региона, в котором среднедушевые денежные доходы населения в месяц на 3% больше среднего по выборке, а уровень безработицы окажется на 2% выше среднего по выборке. Решение: 1. Построим корреляционное поле между потребительскими расходами и среднедушевыми денежными доходами населения в месяц Построим поле корреляции (диаграмму рассеяния). По расположению точек на поле корреляции можно судить о направлении и форме связи между переменными. Поле корреляции представлено на рисунке 1. Вывод. Расположение облака точек на поле корреляции произошло из левого нижнего угла в правый верхний угол. Это говорит о наличии прямой связи между потребительскими расходами в среднем на душу населения и среднедушевыми денежными доходами населения в месяц. Т.е. с увеличением среднедушевых денежных доходов х значения потребительских расходов в среднем на душу населения у тоже в среднем увеличиваются. По форме связи можно предположить линейную зависимость. 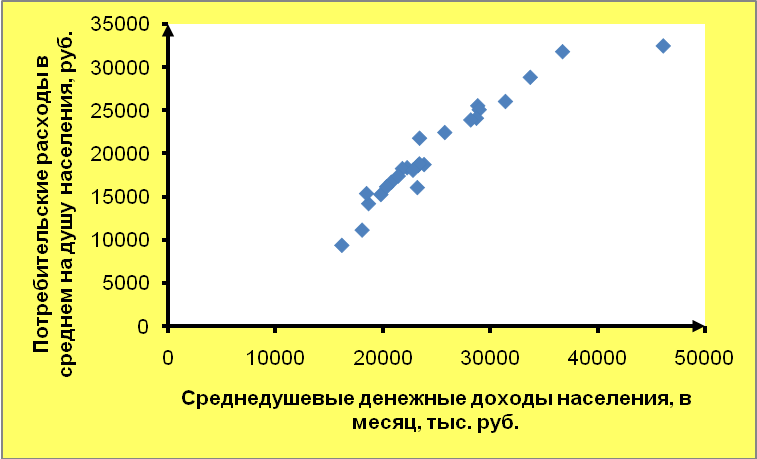 Рисунок 1 – Поле корреляции 2. Оценим тесноту линейной связи между потребительскими расходами и среднедушевыми денежными доходами с надежностью 0,9 Сначала необходимо определить линейный коэффициент парной корреляции. Коэффициент корреляции показывает тесноту и направление линейной связи между переменными. Чем ближе значение коэффициента к единице (по модулю), тем более тесная связь между признаками. Для расчета стром вспомогательную таблицу 2. Расчет средний квадратических отклонений признаков: Расчет коэффициента корреляции: Вывод. Коэффициент корреляции показывает, что связь между потребительскими расходами и среднедушевыми денежными доходами очень тесная и прямая. Таблица 2 Вспомогательная таблица для расчета коэффициента корреляции и построения линейной модели парной регрессии
Выдвигаем нулевую гипотезу о равенстве нулю коэффициента корреляции (незначимости связи между признаками): Альтернативная гипотеза: Для проверки гипотезы рассчитываем значение t-критерия Стьюдента: 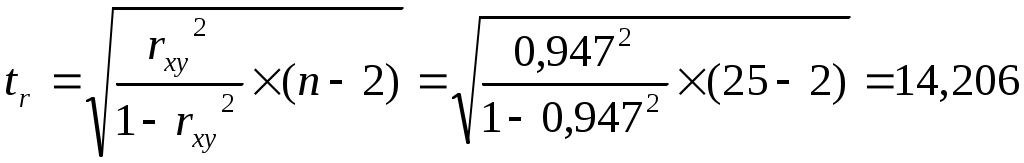 По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости α = 0,1 (доверительная вероятность 90%) и с числом степеней свободы df = n– 2 = 25 – 2 =23: |
