Контрольная работа по эконометрики вариант №8. Задача 1 3 Ситуационная (практическая) задача 2 25 Тестовые задания 32 Список использованной литературы 35
 Скачать 0.84 Mb.
|
Ситуационная (практическая) задача № 2Имеются данные об объеме платных услуг населению, млн. рублей для Новосибирской области за 2010- 2018 г. г. Таблица 6 Динамика объема платных услуг населению
На основе полученных данных требуется: 1. Построить график динамики объема платных услуг населению. 2. С помощью метода серий проверить гипотезу о наличии тренда во временном ряде. 3. Рассчитать коэффициенты автокорреляции. Проверить наличие циклических колебаний во временном ряде. 4. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99. 5. С помощью трендовой модели сделать прогноз объема платных услуг населению на 2021 г. Решение: 1. Построение графика временного ряда График динамики объема платных услуг населению представлен на рисунке 3. 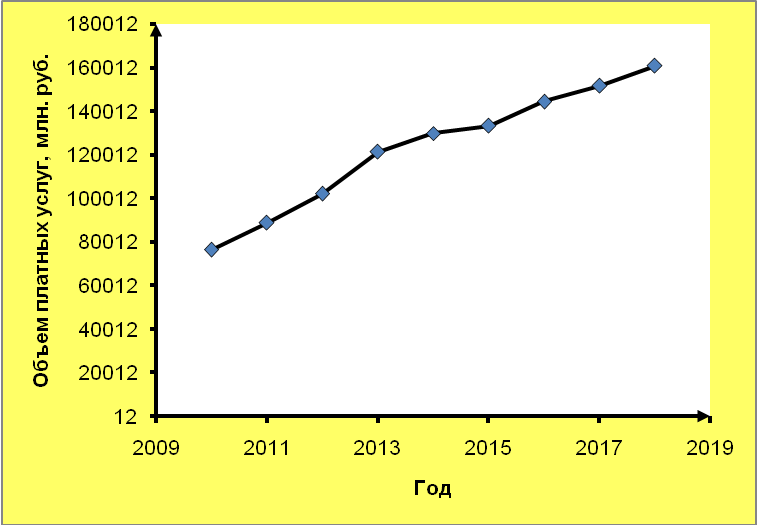 Рисунок 3 – Динамика объема платных услуг населению Вывод. По рисунку 3 видно, что в ряду динамики объема платных услуг населению имеется положительная динамика, ежегодно объем платных услуг населению возрастал, в ряду динамики имеется тенденция к росту. 2. Проверка гипотезы о наличии тренда с помощью метода серий Составляем последовательность: 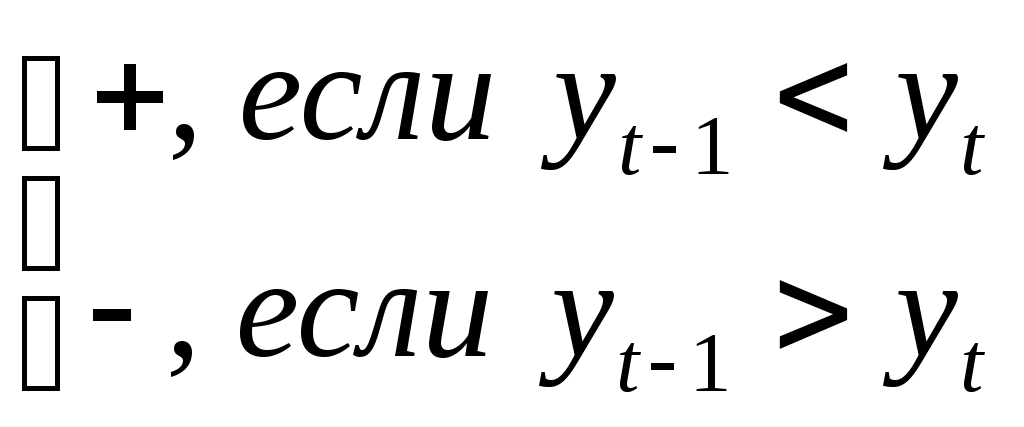 Полученная последовательность "+" и "-" характеризуется количеством серий v(n) = 1 и длиной самой длинной серии t(n) = 8. Проверка гипотезы основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий - слишком маленьким. Поэтому для того, чтобы не была отвергнута гипотеза о случайности исходного ряда (об отсутствии систематической составляющей) должны выполняться следующие неравенства: 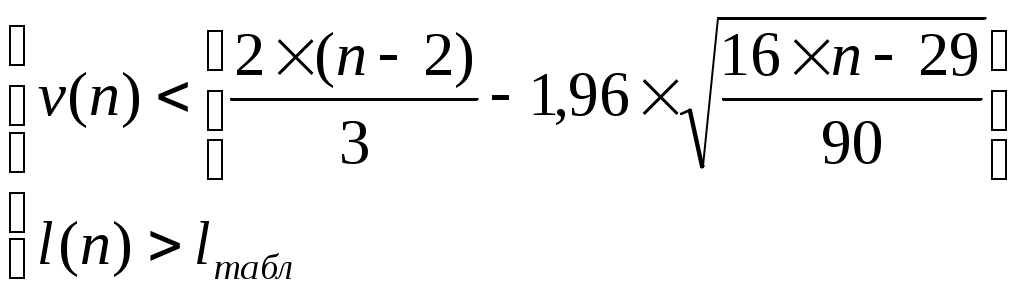 Рассчитываем численное значение для 1-го неравенства:  Поскольку  , то 1-е неравенство выполняется.Находим табличное значение:  Поскольку  , то 2-е неравенство выполняется.Вывод. Оба неравенства выполняются, гипотеза о случайности временного ряда (отсутствие тренда) отвергается, в ряду динамики объема платных услуг населению присутствует трендовая составляющая. Таблица 7 Расчет серий
3. Рассчитаем коэффициенты автокорреляции При наличии тенденции в ряду динамики уровни ряда характеризуются автокорреляцией, т.е. каждый последующий уровень ряда зависит от предыдущего. Для измерения автокорреляции используется коэффициент автокорреляции уровней:  , где - фактические уровни динамического ряда; - уровни того же динамического ряда, но сдвинутые на  шагов во времени; - величина лага (сдвига во времени), определяющая порядок коэффициента автокорреляции.Серию коэффициентов автокорреляции уровней ряда с последовательным увеличением величины лага называют автокорреляционной функцией. Рассчитаем коэффициенты автокорреляции 1-го и 2-го порядков. Вспомогательные расчеты приведены в таблице 8. Расчет коэффициента автокорреляции первого порядка: 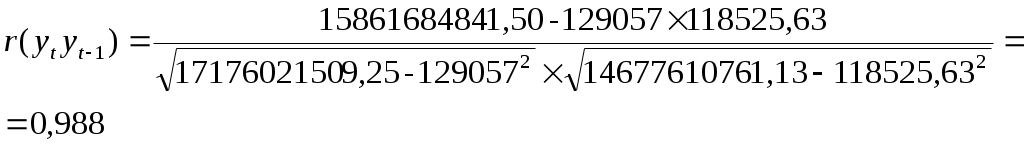 Расчет коэффициента автокорреляции второго порядка: 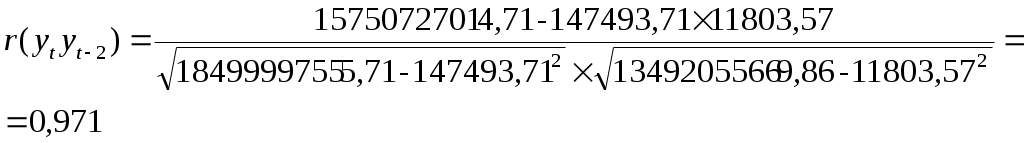 Вывод. Значения коэффициентов автокорреляции первого и второго порядков больше 0,9. Это говорит о сильной тенденции в ряду динамики. Уровни ряда динамики объема платных услуг существенно зависят от предыдущего уровня. Таблица 8 Вспомогательная таблица для расчета коэффициентов автокорреляции
4. Оценка параметров линейной модели тренда Общий вид линейного уравнения тренда:  , гдеа0, а1 – параметры модели. Параметр а1 > 0, в случае положительной динамики у, а1 < 0, в случае отрицательной динамики. Параметры модели можно оценить метод наименьших квадратов (МНК) используя систему нормальных уравнений: 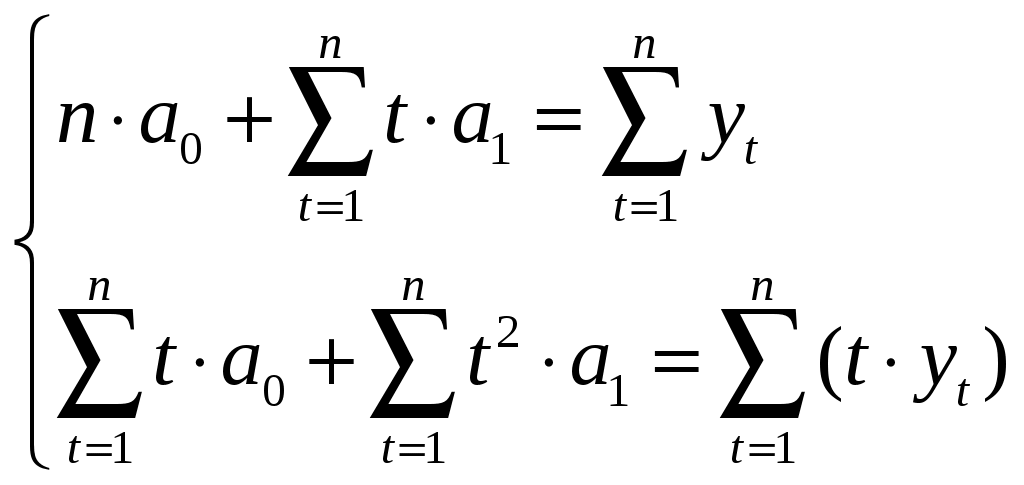 Вспомогательные расчеты приведены в таблице 9. Таблица 9 Вспомогательная таблица для линейной модели тренда
Получили систему нормальных уравнений: 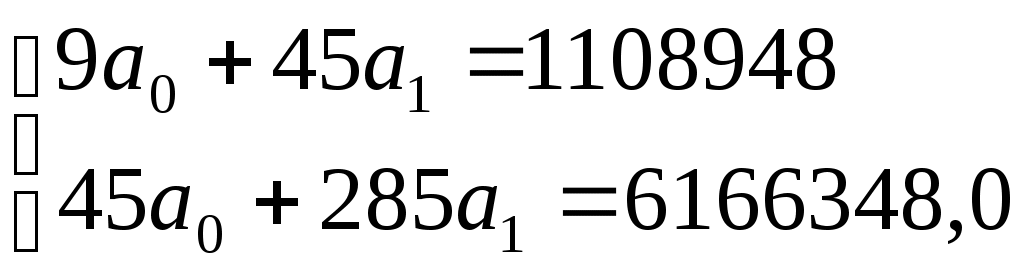 Решая систему относительно неизвестных параметров получаем: а0= 71415,78 а1 = 10360,13 Получили линейное уравнение тренда:  Вывод. По линейной трендовой модели в среднем ежегодно объем платных услуг возрастал на 10360,13 млн. руб. Выровненные уровни объема платных услуг населению получаем путем последовательной подстановки t= 1, 2,…,9 в уравнение тренда.. Рассчитываем случайную компоненту (остатки), как разность фактических и расчетных значений  . Расчет приведен в таблице 9.Коэффициент детерминации: 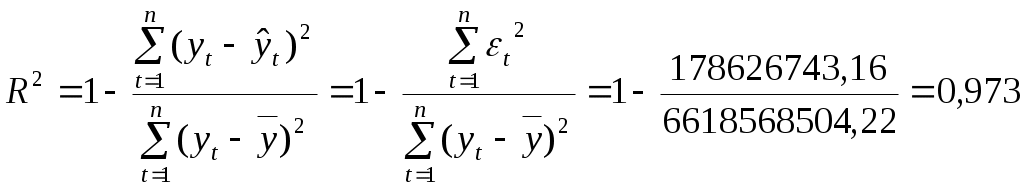 Индекс корреляции:  Вывод. Связь между объемом платных услуг и течением времени заметная. 97,3% вариации объема платных услуг объясняется влиянием фактора времени, остальные 2,7% вариации объема платных услуг происходит под влиянием прочих случайных факторов. Выдвигаем нулевую гипотезу о том, что найденные показатели тесноты связи случайны, т.е. равны нулю:  Для проверки гипотезы рассчитываем значение F-критерия Фишера:  По таблице значений критерия Фишера находим табличное (критическое) значение критерия на уровне значимости α = 0,01 и с числом степеней свободы df1 = 1 и df2 = n– 2 = 9 – 2 = 7: Fтабл = 12,246 Вывод. Поскольку Fтабл < F, то нулевую гипотезу о незначимости показателей корреляции и детерминации отклоняем с вероятностью допустить ошибку в 1%. Построенная линейная модель тренда является статистически значимой. Показатели тесноты и силы связи не случайны.4. Построим прогноз объема платных услуг населению на 2021 г. Прогнозное значение фактора времени:  Прогнозное значение результативного признака (точечный прогноз):  71415,78 + 10360,13×12 = 195737,38 млн. руб.Вывод. По линейной трендовой модели можно ожидать, что в 2021 году объем платных услуг населению составит 195737,38 млн. руб. 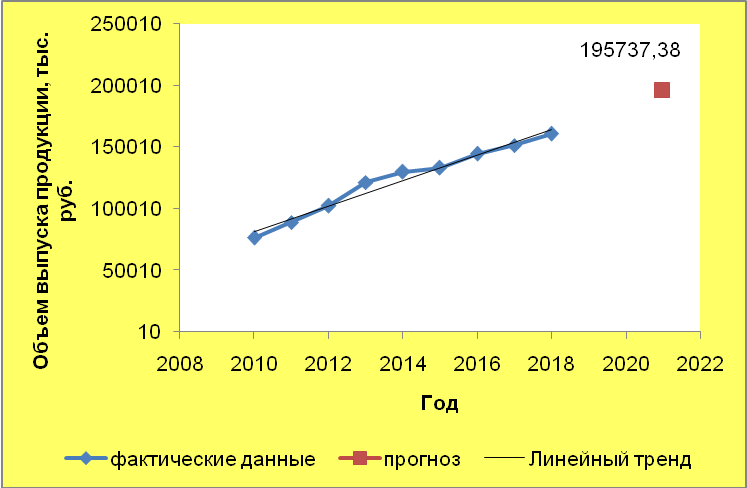 Рисунок 4 – Результаты моделирования и прогнозирования |
