Контрольная работа по эконометрики вариант №8. Задача 1 3 Ситуационная (практическая) задача 2 25 Тестовые задания 32 Список использованной литературы 35
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
Вывод. Средняя относительная ошибка аппроксимации показывает, что в среднем фактические значения потребительских расходов в среднем на душу населения у отличаются от полученных по модели на 7,23%. Т.к. ошибка меньше 10%, то модель считается точной. 7. Дадим прогноз потребительских расходов в среднем на душу населения с надежностью γ = 0,9 для гипотетического региона, в котором среднедушевые денежные доходы населения в месяц на 3% больше среднего по выборке Прогнозное значение факторного признака: Прогнозное значение результативного признака (точечный прогноз): Рассчитываем среднюю квадратическую ошибку прогноза: 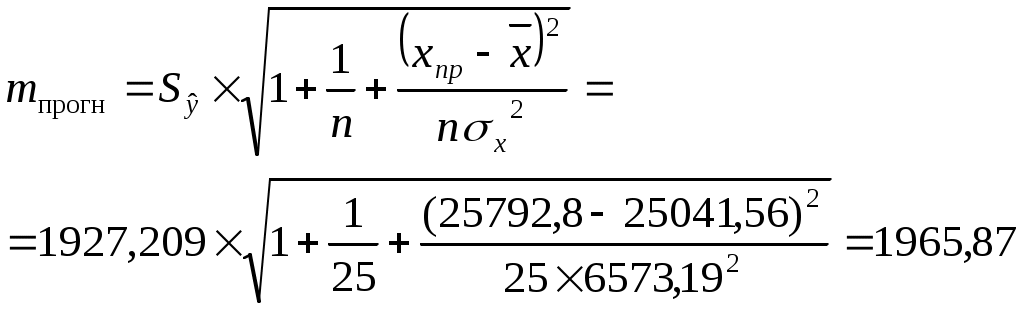 Табличное (критическое) значение критерия на уровне значимости α = 0,1 и с числом степеней свободы df = n– 2 = 25 – 2 =23: Рассчитываем доверительный интервал: Нижняя граница прогноза: Верхняя граница прогноза: Вывод. С вероятностью 90% можно утверждать, что если значение среднедушевых денежных доходов населения в месяц х составит 25792,8 руб., то величина потребительских расходов в среднем на душу населения у будет находится в пределах от 17405,65 до 24144,14 руб. 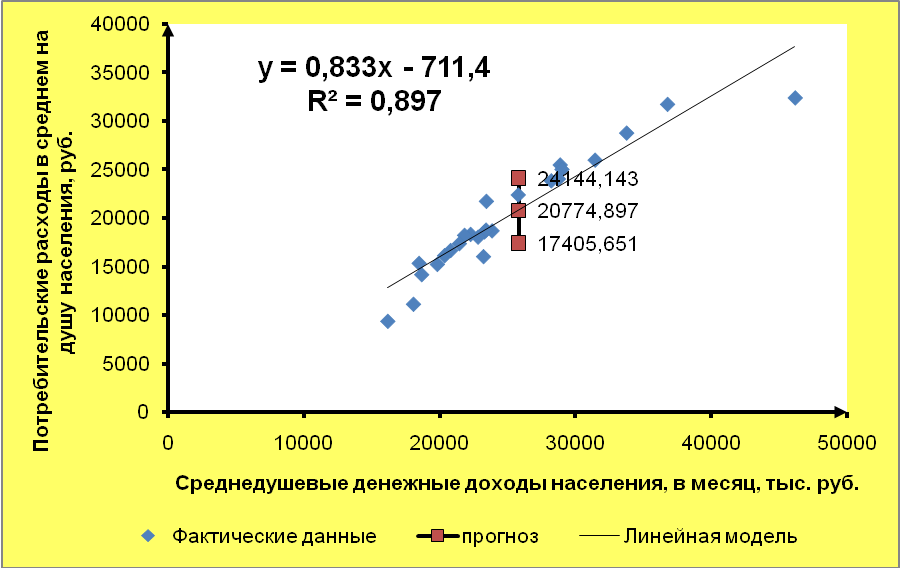 Рисунок 2 – Результаты моделирования и прогнозирования 8. Рассчитаем коэффициенты линейного уравнения множественной регрессии для зависимости потребительских расходов в среднем на душу населения от среднедушевых денежных доходов населения и уровня безработицы Общий вид линейного двухфакторного уравнения регрессии: Вектор неизвестных параметров методом наименьших квадратов рассчитывается по формуле: 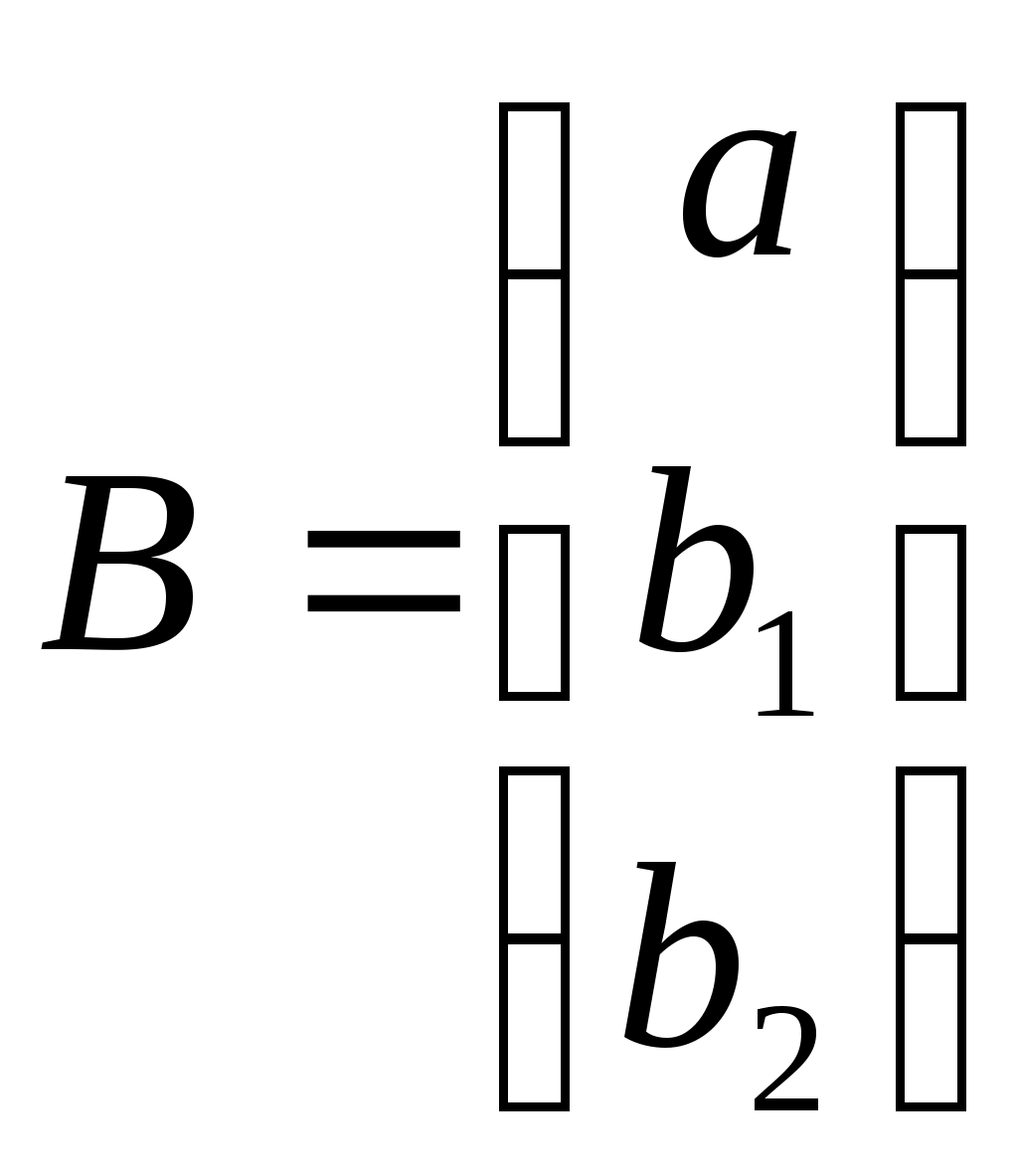 - вектор значений параметров модели; - вектор значений параметров модели;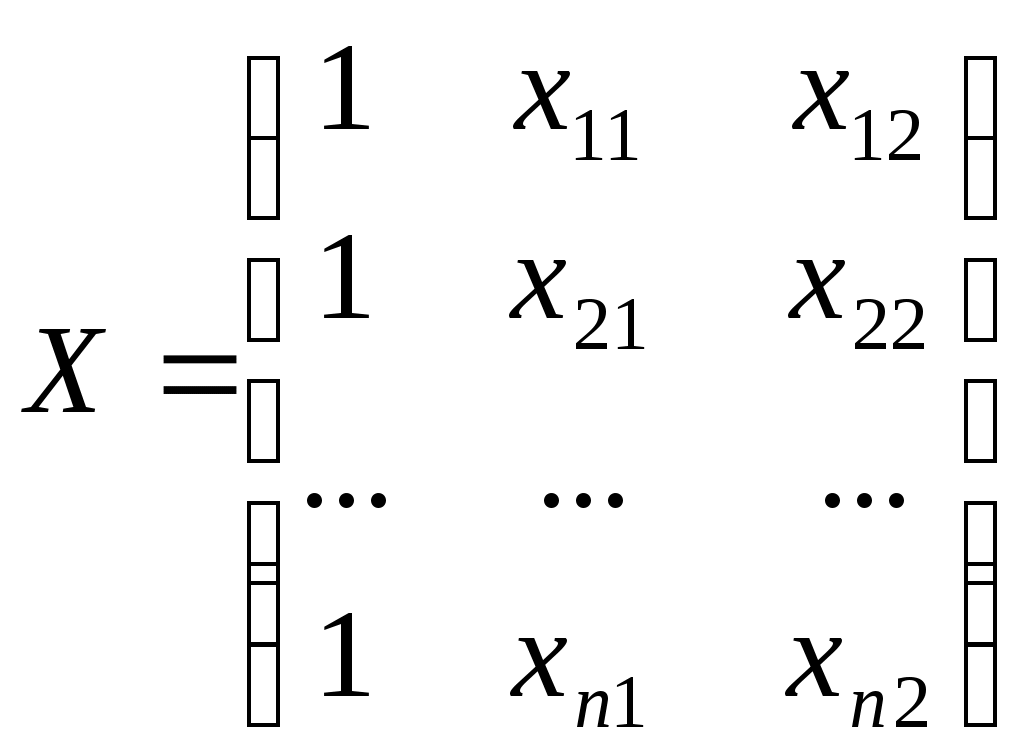 - матрица значений факторов (столбец единиц представляет собой свободный член); - матрица значений факторов (столбец единиц представляет собой свободный член);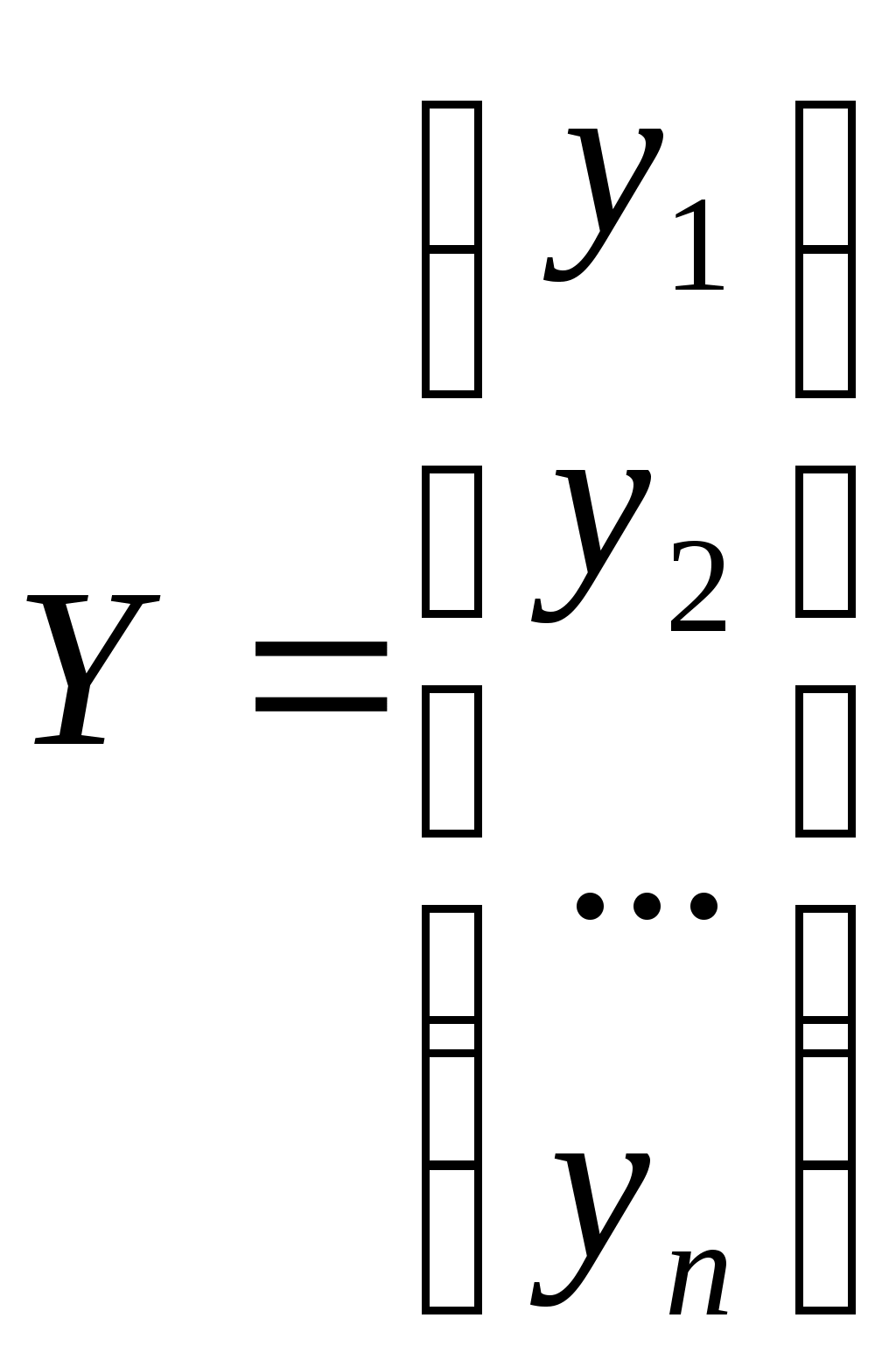 - вектор значений результативного признака. - вектор значений результативного признака.Неизвестные параметры модели можно определить, решив систему нормальных уравнений: 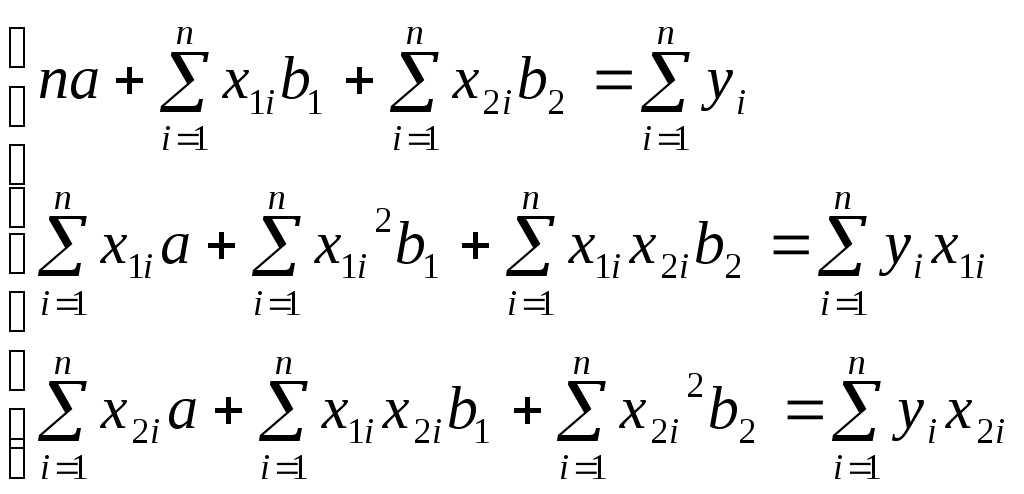 Вспомогательные промежуточные расчеты сумм представлены в таблице 2 и 4. П  олучаем систему: олучаем систему:
Таблица 4 Вспомогательная таблица для построения двухфакторной модели регрессии
Решая систему относительно неизвестных параметров, получаем: 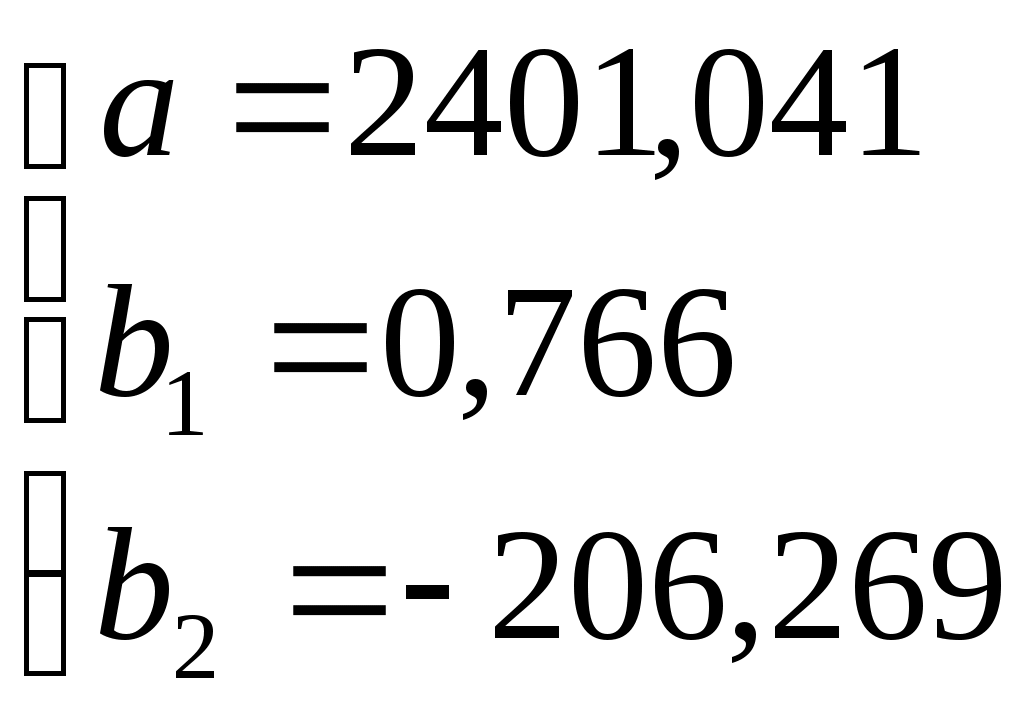 Получили двухфакторную модель регрессии: Вывод. Коэффициент регрессии Коэффициент регрессии Теоретические (расчетные) значения результативного показателя Рассчитываем остатки, как разность фактических и расчетных значений: Расчет представлен в таблице 5. 9. Дадим интервальные оценки параметров Остаточная сумма квадратов отклонений: Рассчитываем среднюю квадратическую ошибку модели: 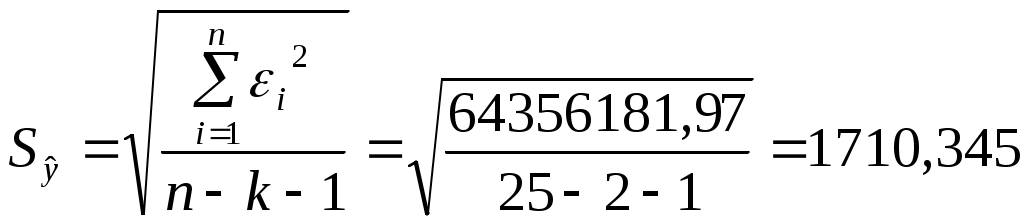 Стандартные ошибки параметров рассчитывают по формуле: 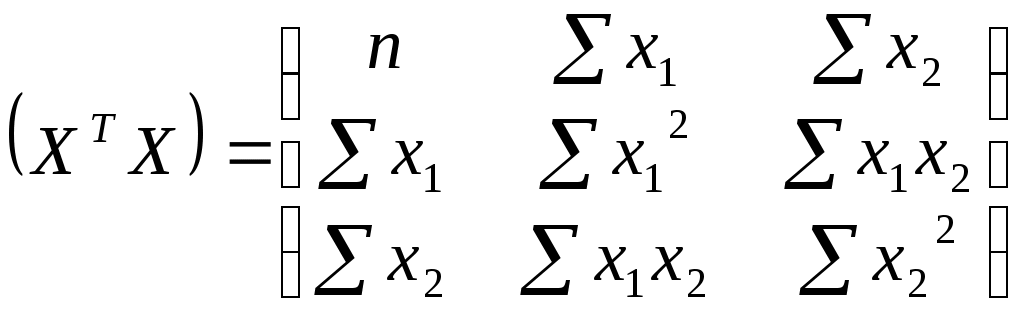 Находим обратную матрицу  Стандартные ошибки параметров модели: Табличное (критическое) значение критерия на уровне значимости α = 0,1 и с числом степеней свободы df = n– k – 1 = 25 – 3 = 22: Доверительный интервал для свободного члена а: Вывод. В доверительный интервал попадает 0, свободный член не является статистически значимым. Доверительный интервал для коэффициента регрессии b1: Вывод. С вероятностью 90% значение коэффициента регрессии b1 будет находится в пределах от 0,594 до 0,865. Т.е. с вероятностью 90% при увлечении среднедушевых денежных доходов населения в месяц х1 на 1 руб. значение потребительских расходов на душу населения у возрастет не менее, чем на 0,594, но не более чем на 0,865 руб. Т.к. в доверительный интервал не попадает 0, то параметр является статистически значимым. Доверительный интервал для коэффициента регрессии b2: -206,269 Вывод. С вероятностью 90% значение коэффициента регрессии b2 будет находится в пределах от -206,269 до -74,290. Т.е. с вероятностью 90% при увлечении уровня безработицы х2 на 1 % значение потребительских расходов на душу населения у снизится не менее, чем на 74,29 руб., но не более чем на 206,269 руб. Т.к. в доверительный интервал не попадает 0, то параметр является статистически значимым. 10. Оценим статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 Выдвигаем нулевые гипотезы о том, что найденные параметры не являются статистически значимыми: Для проверки гипотез рассчитывают t-критерий Стьюдента по формулам: Расчет фактических значений критерия Стьюдента: Вывод. Поскольку Поскольку Таблица 5 Вспомогательная таблица для оценки качества модели
11. Проверим качество построенного уравнения регрессии Рассчитываем множественный коэффициент детерминации: 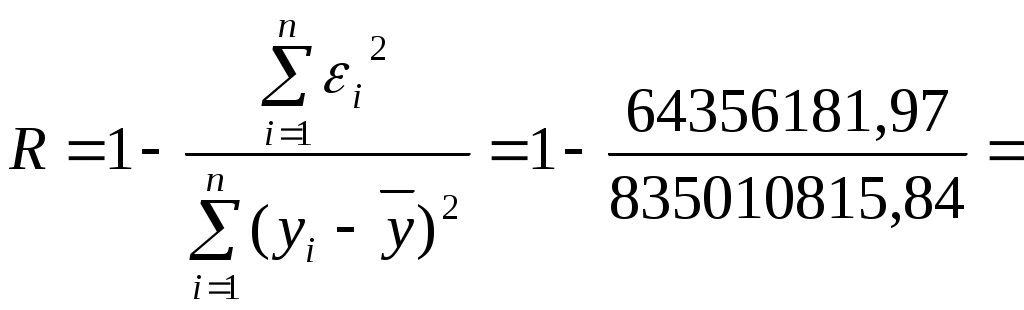 0,923 0,923Вывод. Коэффициент показывает, что 92,3% вариации потребительских расходов на душу населения у происходит под влиянием факторов х1 и х2, включенных в модель. Остальные 7,3% вариации величины потребительских расходов на душу населения у объясняется влиянием прочих случайных факторов. Скорректированный коэффициент детерминации позволяет учесть при оценке качества модели соотношение количества наблюдений и количества оцениваемых параметров модели. Вывод. Показатели детерминации говорят о хорошем качестве модели регрессии. Выдвигаем нулевую гипотезу о том, что найденные показатели тесноты и силы связи случайны, т.е. равны нулю: Альтернативная гипотеза: Для проверки нулевой гипотезы рассчитываем значение F-критерия Фишера: Табличное значение F – критерия при уровне значимости α = 0,1 и числе степеней свободы d.f.1= k = 2 (количество факторов), числе степеней свободы d.f.2= (n – k– 1) = (25 – 2 – 1) = 22 составит Fтабл = 2,561 Вывод. Поскольку 12. Проверим построенное уравнение на наличие мультиколлинеарности Расчет средних квадратических отклонений: Факторы, включаемые в модель должны быть слабо связаны между собой, факторы не должны быть коллинеарными (линейнозависимыми). Коэффициент парной корреляции между факторами: Вывод. Связь между факторами х1 и х2 умеренная и обратная. Выдвигаем нулевую гипотезу о равенстве нулю коэффициента корреляции для генеральной совокупности (незначимости связи между признаками): Альтернативная гипотеза: Для проверки гипотезы рассчитываем значение t-критерия Стьюдента: 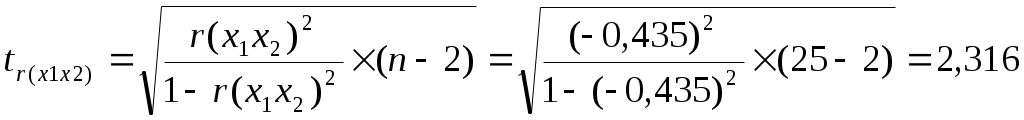 По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости α = 0,1 и с числом степеней свободы df = n– 2 = 25 – 2 =23: Вывод. Поскольку Для более точной оценки мультиколлинеарности проверим гипотезу о независимости объясняющих переменных, т.е. проведем тест на выявление мультиколлинеарности Фаррара – Глоубера. Находим определитель матрицы парных коэффициентов корреляции между факторами: Находим расчетное значение статистики Фаррара – Глоубера: 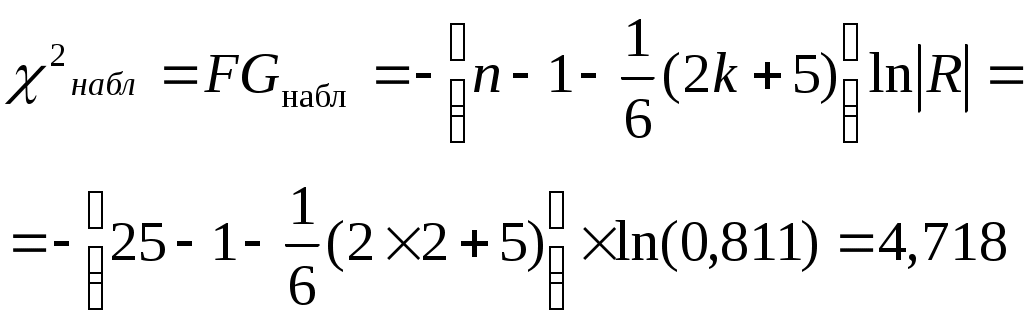 Находим табличное (критическое) значение на уровне значимости α = 0,1 и с числом степеней свободы df= 1: Вывод. Т.к. Оба фактора вместе в модель включать не следует. 13. Дадим прогноз потребительских расходов в среднем на душу населения с надежностью γ = 0,9 для гипотетического региона, в котором среднедушевые денежные доходы населения в месяц на 3% больше среднего по выборке, а уровень безработицы окажется на 2% выше среднего по выборке Прогнозное значение факторных признаков: Вектор прогнозных значений факторных признаков: 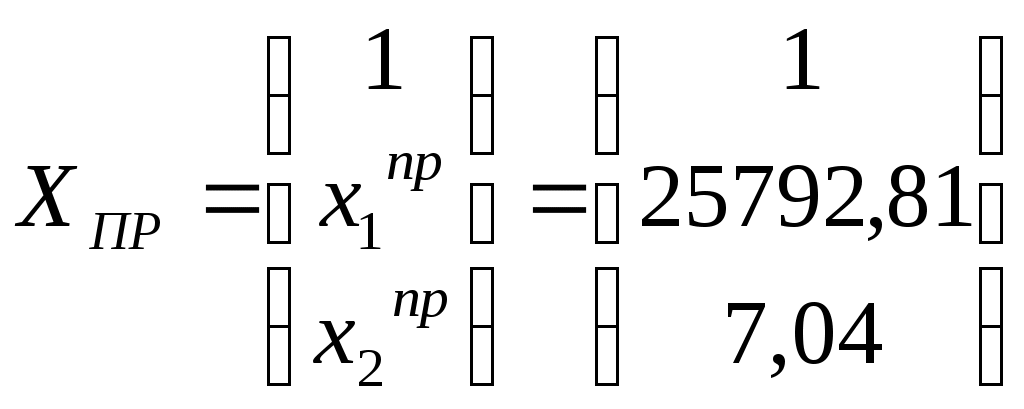 Прогнозное значение результативного признака (точечный прогноз): - 206,269×7,04 = 20695,75 Средняя квадратическая ошибка прогноза рассчитывается по формуле: 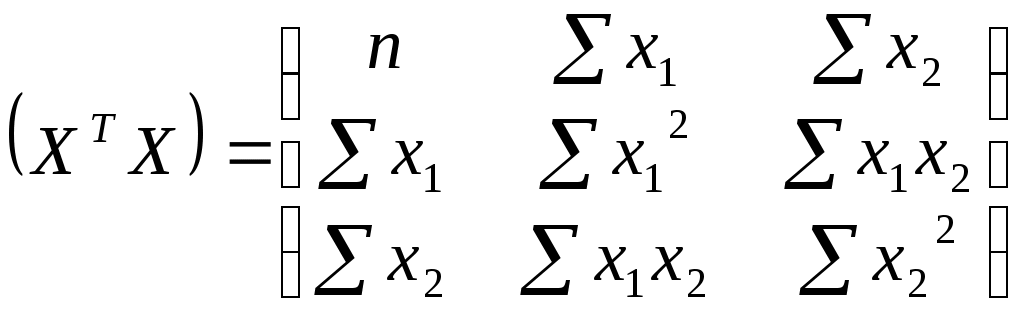 Находим среднюю квадратическую ошибку прогноза: Табличное (критическое) значение критерия на уровне значимости α = 0,1 и с числом степеней свободы df = n– k – 1 = 25 – 3 = 22: Рассчитываем доверительный интервал: Нижняя граница прогноза: Верхняя граница прогноза: Вывод. С вероятностью 90% можно утверждать, что при среднедушевых денежных доходов населения в 25792,81 руб. и уровне безработицы в 7,04% величина потребительских расходов на душу населения у будет находится в пределах от 17699,50 до 23692,01 руб. |
