Лекция 1. Лекция 1 Предмет начертательной геометрии. История развития начертательной геометрии
 Скачать 5.78 Mb. Скачать 5.78 Mb.
|
|
Конспект лекций. «Инженерная и компьютерная графика» Лекция № 1 Предмет начертательной геометрии. История развития начертательной геометрии. «Искусство представлять на листе бумаги, имеющем только два измерения, предметы, имеющие три размера, которые подчинены точному определению». Гаспар Монж Изучает: - методы изображения пространственных геометрических фигур на плоскости (поверхности) - способы решения метрических и позиционных задач в пространстве по этим изображениям. Начертательная геометрия как наука была создана в конце XVIII века великим французским геометром и инженером Гаспаром Монжем.  Гаспар Монж (1746-1818) Основы графических изображений росписи в пещерах-35-12 тысячелетия до н. э. появления чертежей -плана дома XXIV-XXIII вв. до н.э. из района Месопотамии. План вавилонского дома с разрезом по дверным и оконным проемам и указанием клинописью размеров (ок. 1894 - 1595 гг. до н. э.). Древний Египет – развитие арифметики и геометрии Древняя Греция и Рим – геометрия, 5 постулатов Евклида, Витрувий -применил три проекции: план, фасад и профиль. Период Возрождения - совершенствование приемов построения перспективы итальянскими художниками и архитекторами (Леонардо да Винчи, Рене Декарт, Жирар Дезарг) Русские изобретатели - И.И. Ползунов (1728-1766) И.П. Кулибин (1735-1818) Неэвклидова геометрия - Николай Лобачевский (1792-1856) Бернгард Риман (1826-1866) и др. Гаспар Монж (1746-1818) В России – Институт Корпуса инженеров путей сообщения (2 декабря 1809 г.) - К.И. Потье, Ю Я.А. Севастьянов, Н.И. Макаров, В.И. Курдюмов, Н.А. Рынин и др. Принятые обозначения
Символы отношений между геометрическими фигурами
Образование проекций Проецирование — это процесс получения проекций объекта на какой-либо плоскости (поверхности) с помощью проецирующих лучей.  A'= ℓ ∩ π1 (A ∈ ℓ) Проекцией точки A на плоскость проекций называется точка пересечения проецирующей прямой l, проходящей через точку A, с плоскостью проекций. Методы проецирования В зависимости от положения центра проецирования различают следующие виды проецирования:  Центральным называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S — центра проецирования. Параллельным называется такое проецирование, при котором все проецирующие лучи параллельны заданному направлению s. Параллельное проецирование представляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций. При заданном аппарате проецирования каждой точке пространства соответствует только одна точка на плоскости проекций. Одна проекция точки не определяет положения этой точки в пространстве. 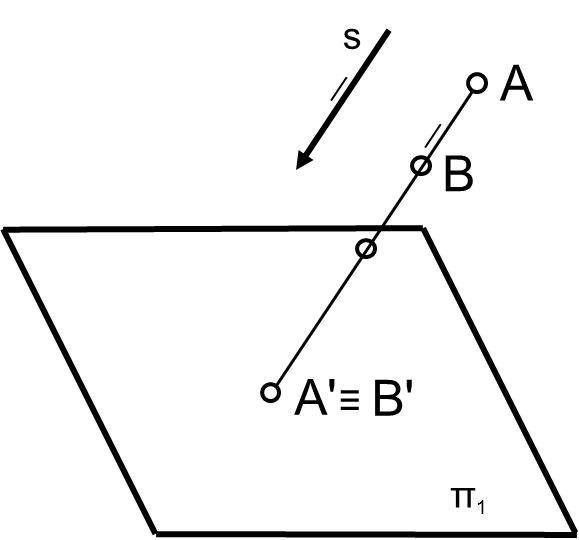 Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве. Проекционный чертёж становится обратимым при введении дополнительной информации. Обратимость чертежа может быть обеспечена проецированием на две (три) непараллельные плоскости проекций. 5. Параллельное проецирование. Инвариантные свойства параллельного проецирования.  1. Проекция точки есть точка. 2.Проекция прямой, в общем случае, прямая. 3.Если точка принадлежит прямой, то и проекция этой точки принадлежит проекции прямой. 4.Если точка делит отрезок прямой в каком-то отношении, то и проекция этой точки делит проекцию отрезка в таком же отношении.  5.Проекция точки пересечения прямых есть точка пересечения проекций этих прямых. 6.Проекции параллельных прямых параллельны. 7.Прямая, параллельная направлению проецирования, проецируется в точку.  8.Плоский многоугольник в общем случае проецируется в многоугольник с тем же количеством вершин. 9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре. 9.1 Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку. 9.2 Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу. 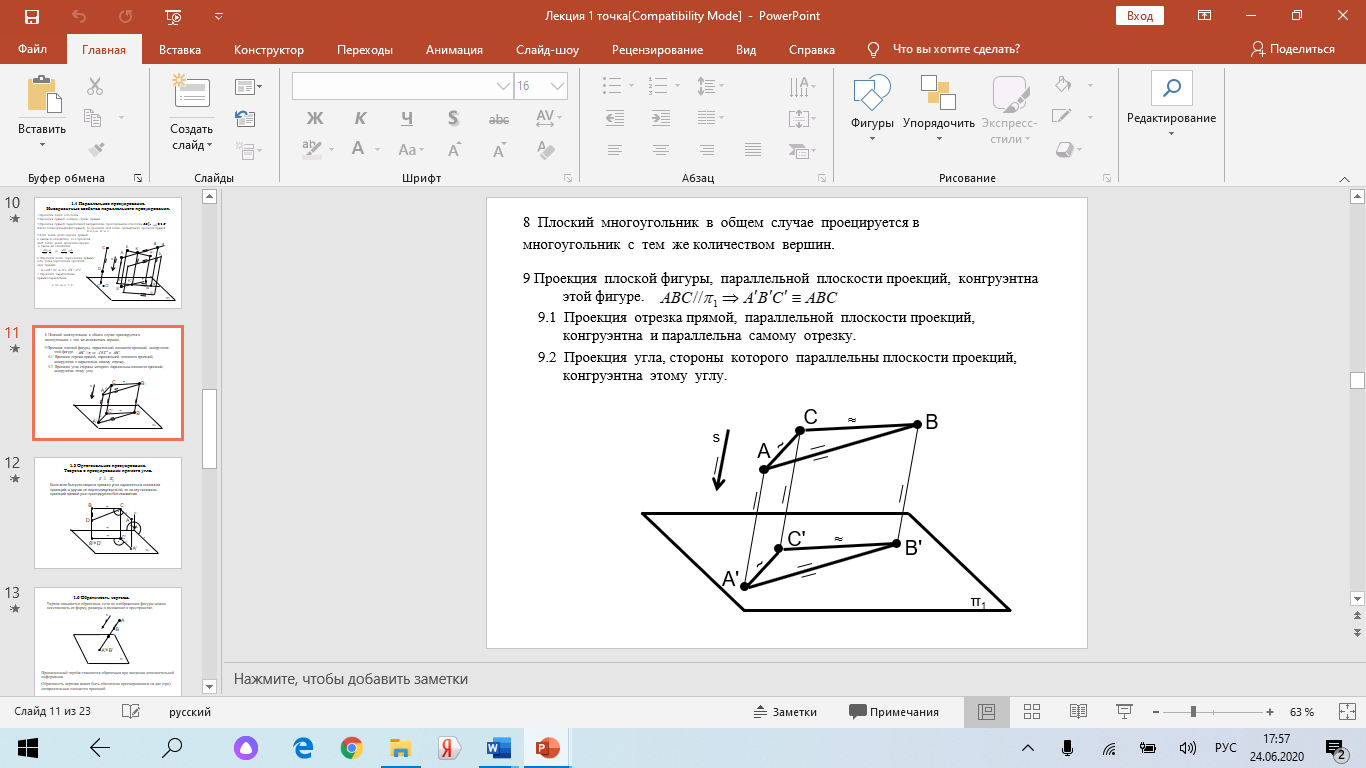 6. Ортогональное проецирование. Теорема о проецировании прямого угла.  Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость проекций прямой угол проецируется без искажения.  7. Обратимость чертежа. Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве. 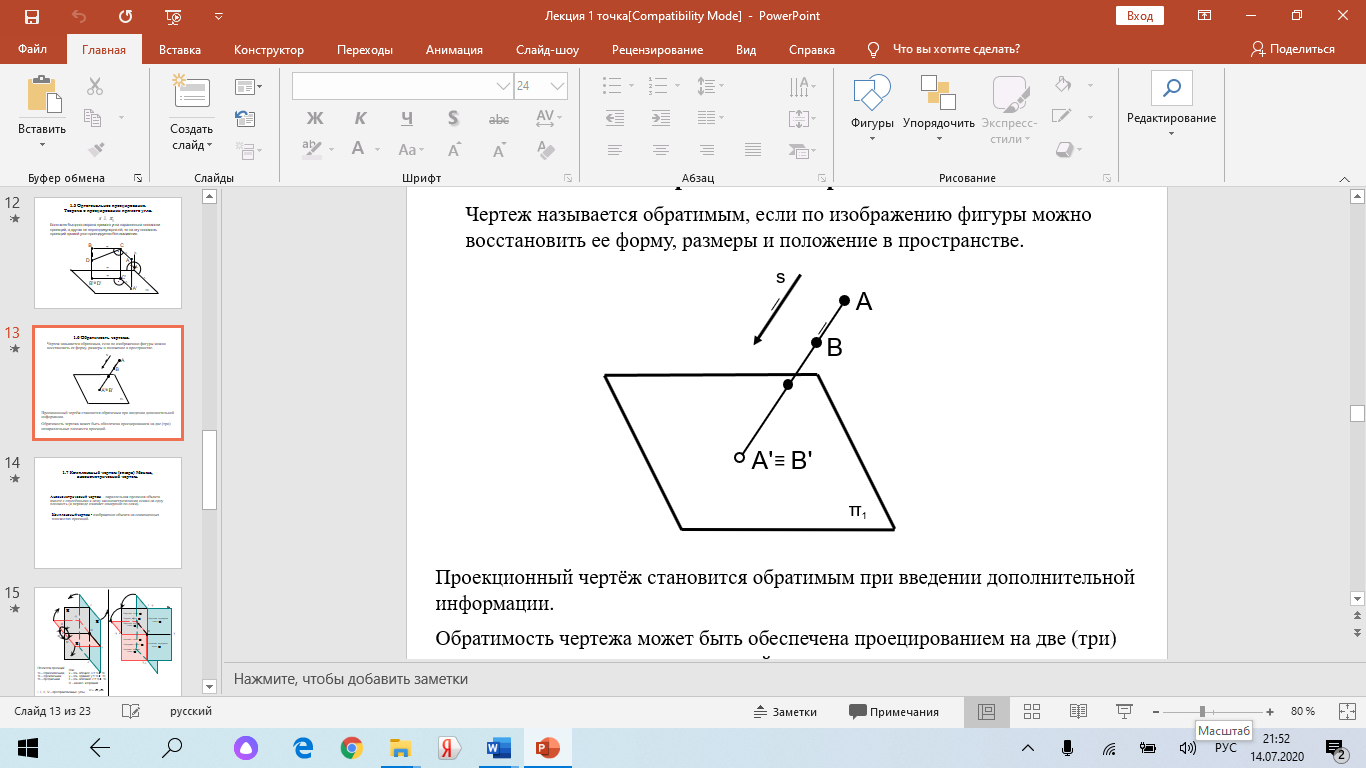 По одной заданной проекции точки (А‘, В‘) невозможно восстановить её положение в пространстве. Точка может находиться в любом месте проецирующего луча. Проекционный чертёж становится обратимым при введении дополнительной информации. Обратимость чертежа может быть обеспечена проецированием на две (три) непараллельные плоскости проекций. 8. Система плоскостей проекций. Эпюра Монжа. Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей — системы трех взаимно перпендикулярных координатных плоскостей.  Для того чтобы получить плоскую (двумерную) модель пространственных координатных плоскостей проекций, горизонтальную и профильную плоскости совмещают с фронтальной (плоскостью чертежа). Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюрой Монжа. 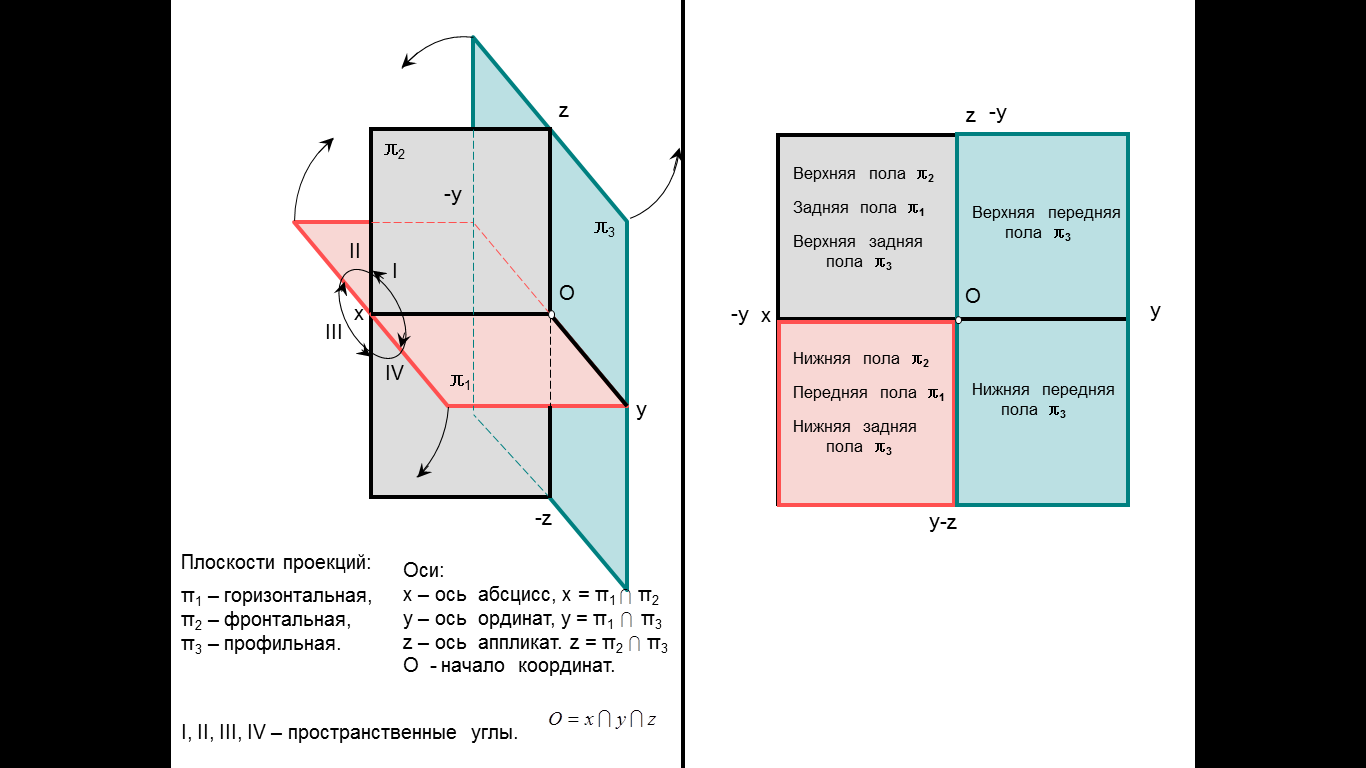 9. Проецирование точки в четырех пространственных углах.     10. Прямая. Способы задания прямой на эпюре. Частные положения прямой в пространстве. По второму инвариантному свойству параллельного проецирования проекция прямой, не перпендикулярной плоскости проекций, есть прямая.  Прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций. 11. Прямые уровня. Прямые параллельные плоскостям проекций (прямые уровня). - Горизонтальная прямая (h); - Фронтальная прямая (f); - Профильная прямая (p). Горизонтальная прямая  Фронтальная прямая   12. Прямые принадлежащие плоскостям проекций  13. Проецирующие прямые (перпендикулярные плоскостям проекций).  14. Взаимное положение прямых. Пересекающиеся, скрещивающиеся и параллельные прямые. 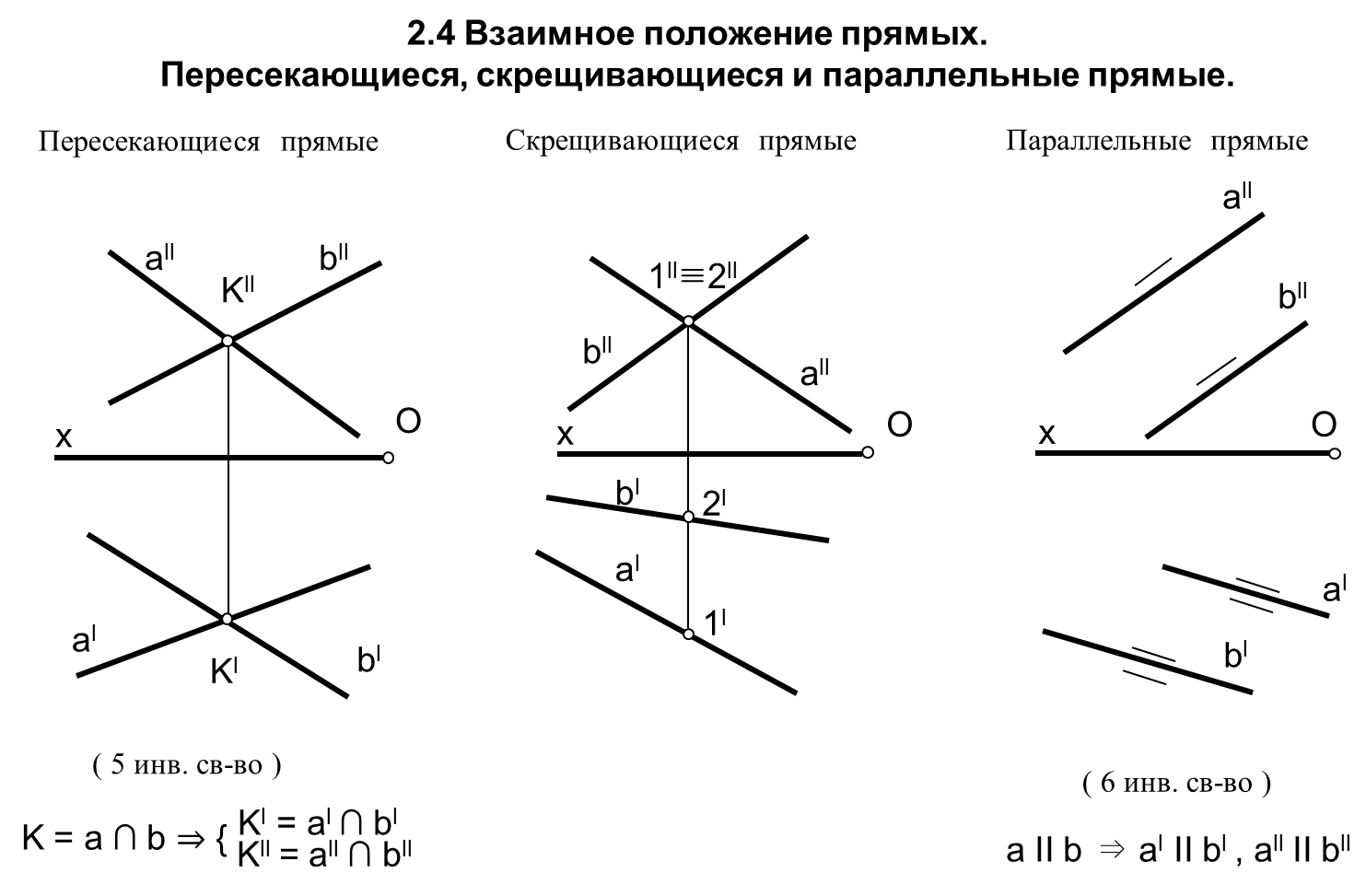 15. Метод конкурирующих точек. Метод конкурирующих точек используется для определения взаимной видимости однихгеометрических объектов относительно других. Это придаёт эпюре большую наглядность. Конкурирующими называются точки, у которых совпадают две какие-либо одноименные проекции. Считается, что наблюдатель смотрит на плоскости проекций из бесконечности. Лучи зрения совпадают с проецирующими прямыми и направлены на горизонтальную плоскость - сверху, на фронтальную плоскость - спереди, на профильную – слева. Видимы точки, находящиеся ближе к наблюдателю, т.е. дальше от плоскостей проекций  16. Проецирование плоскостей. Способы задания плоскостей на эпюре.  1. Тремя точками, не лежащими на одной прямой. 2. Прямой и точкой вне ее. 3. Двумя пересекающимися прямыми. 4. Двумя параллельными прямыми. 5. Плоской фигурой. 6. Следами. На эпюре плоскость задаётся проекциями этих элементов.  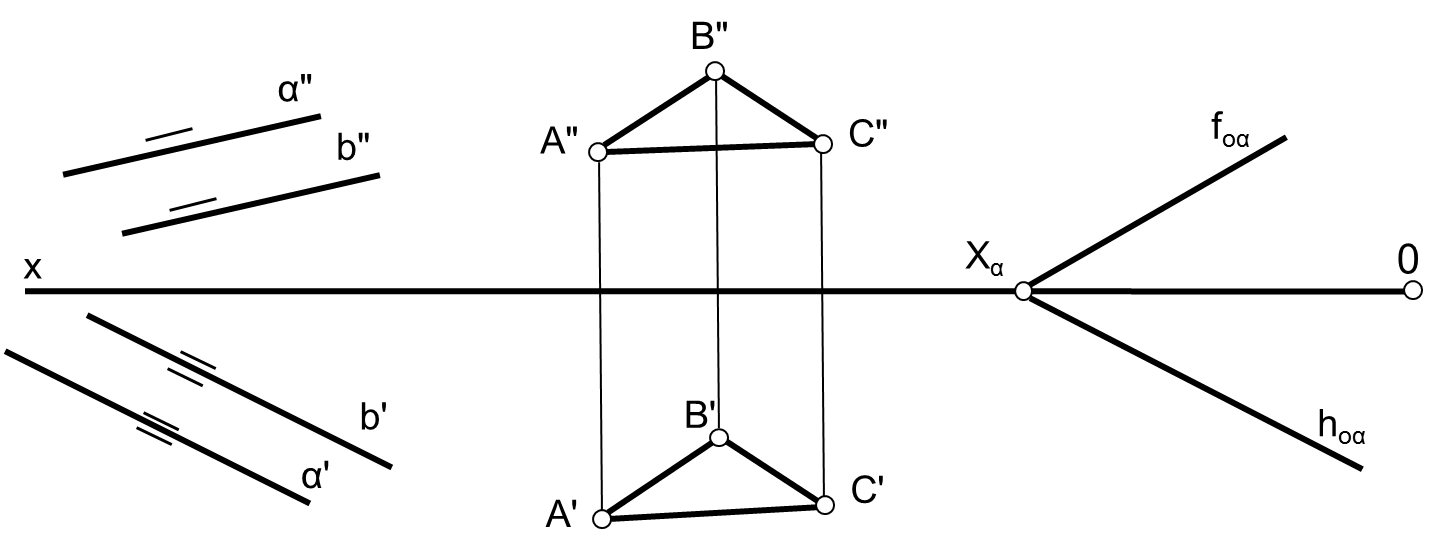 Следом плоскости называется линия (прямая) пересечения плоскости с плоскостью проекций.  17. Главные линии плоскости Горизонталь плоскости - прямая (h), принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций  Фронталь плоскости - прямая (f), принадлежащая этой плоскости и параллельная фронтальной плоскости проекций 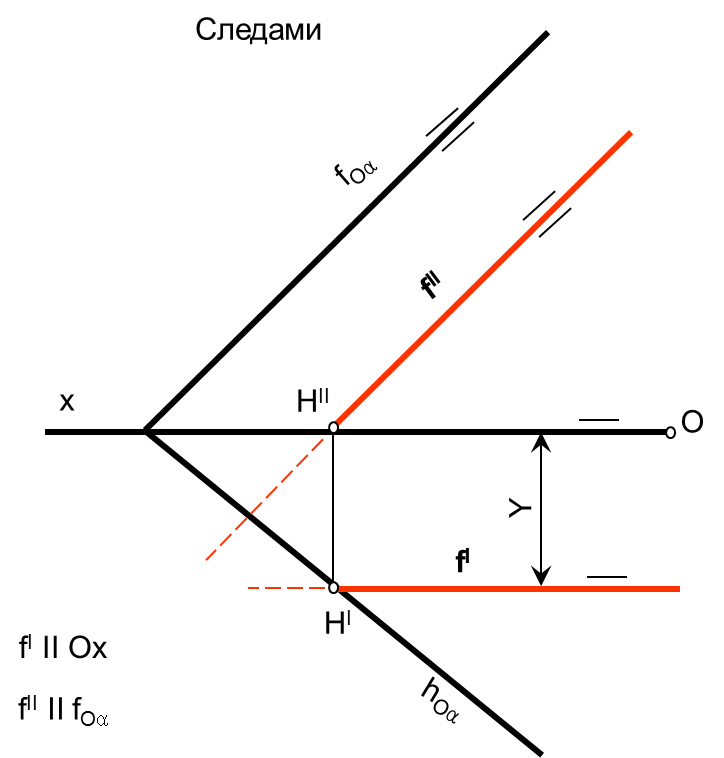  Линия наибольшего ската плоскости - прямая (g), принадлежащая этой плоскости и перпендикулярная её горизонталям. 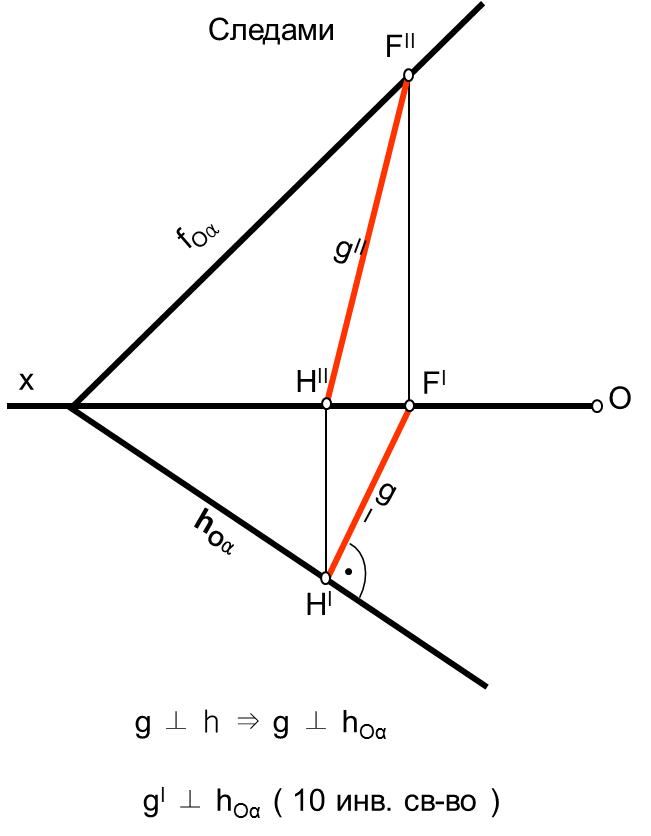  18. Частные положения плоскостей в пространстве. Проецирующие плоскости. Проецирующей называется плоскость перпендикулярная плоскости проекций (┴ πi). Горизонтально проецирующая плоскость α ⊥ π1   Фронтально проецирующая плоскость β ⊥ π2  Профильно проецирующая плоскость ⊥ π3  19. Частные положения плоскостей в пространстве. Плоскости уровня. Плоскость уровня – плоскость параллельная плоскости проекций (параллельна одной и перпендикулярна двум другим). Горизонтальная плоскость γ II π1  Фронтальная плоскость δ II π2  Профильная плоскость η II π3   20. Плоскость односторонней и двухсторонней видимости 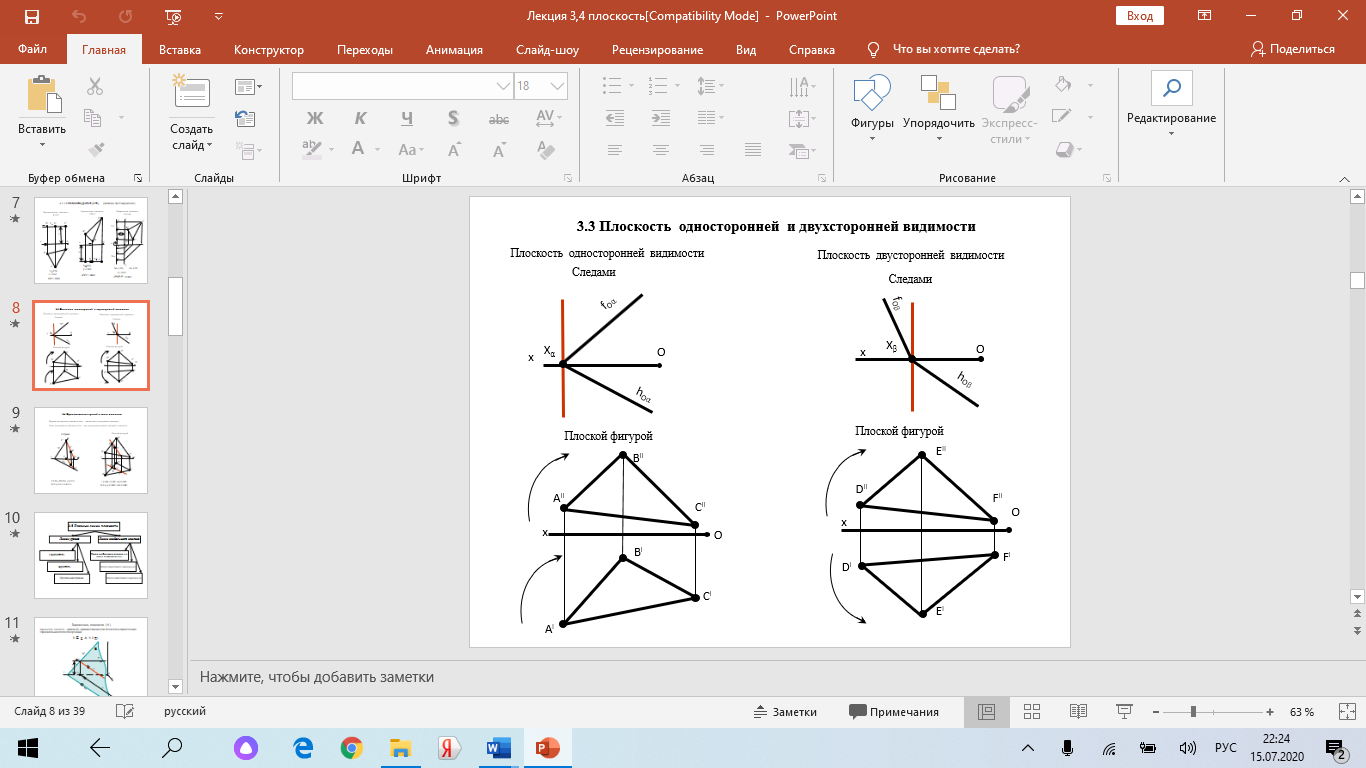 21. Взаимное положение прямой и плоскости. Прямая принадлежащая и параллельная плоскости. Прямая «а» принадлежит плоскости, если две ее точки принадлежат этой плоскости.   Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости.   22. Взаимное положение прямой и плоскости. Прямая перпендикулярная плоскости. Прямаяперпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим вэтой плоскости Чтобы эти прямые углы спроецировались в натуральную величину (см. теорему о проецировании прямого угла), прямые должны быть параллельны плоскостям проекций, т. е. являться горизонталью и фронталью плоскости. Следовательно, прямая a перпендикулярна плоскости, если она перпендикулярна пересекающимся горизонтали h и фронтали f этой плоскости.   23. Взаимное положение плоскостей. Параллельные и перпендикулярные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.   Плоскости перпендикулярны, если одна плоскость проходит через перпендикуляр к другой плоскости.  Поверхности вращения. Принадлежность линий и точек Поверхностью вращения называют поверхность, образующуюся вращением произвольной линии (плоской или пространственной) вокруг оси i.  Точка принадлежит поверхности, если она принадлежит линии, лежащей на поверхности. Линия принадлежит поверхности, если все её точки принадлежат поверхности. Рассмотрим основные типы поверхностей вращения: 1. Конус; 2. Цилиндр; 3. Сфера; 4. Тор. 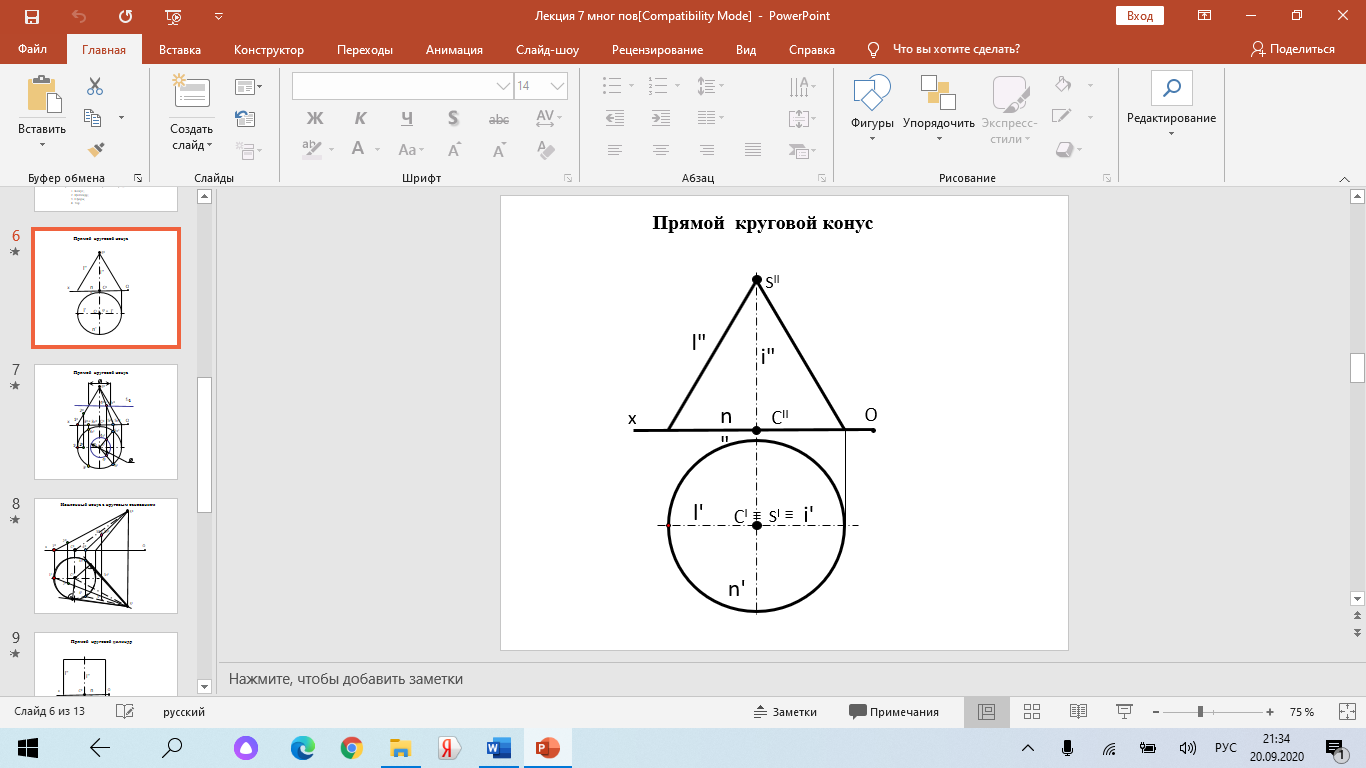  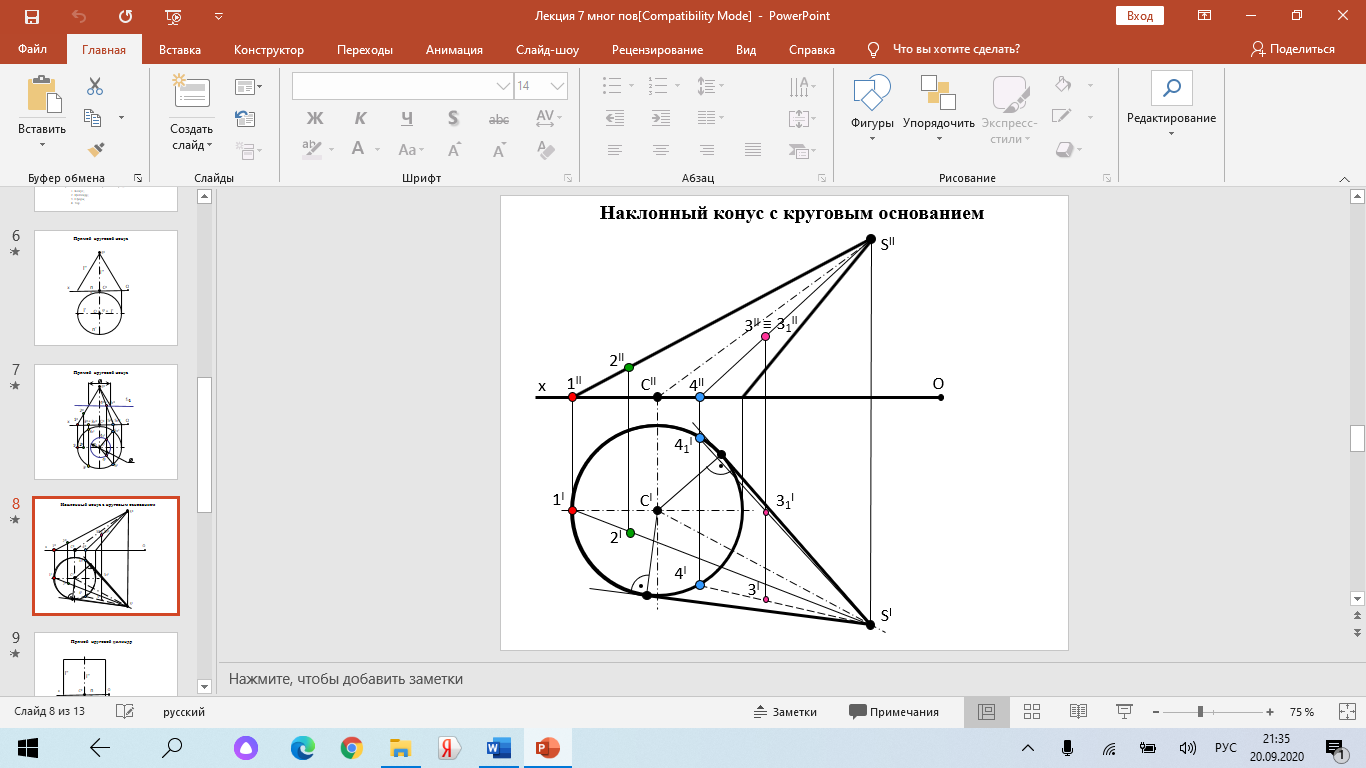 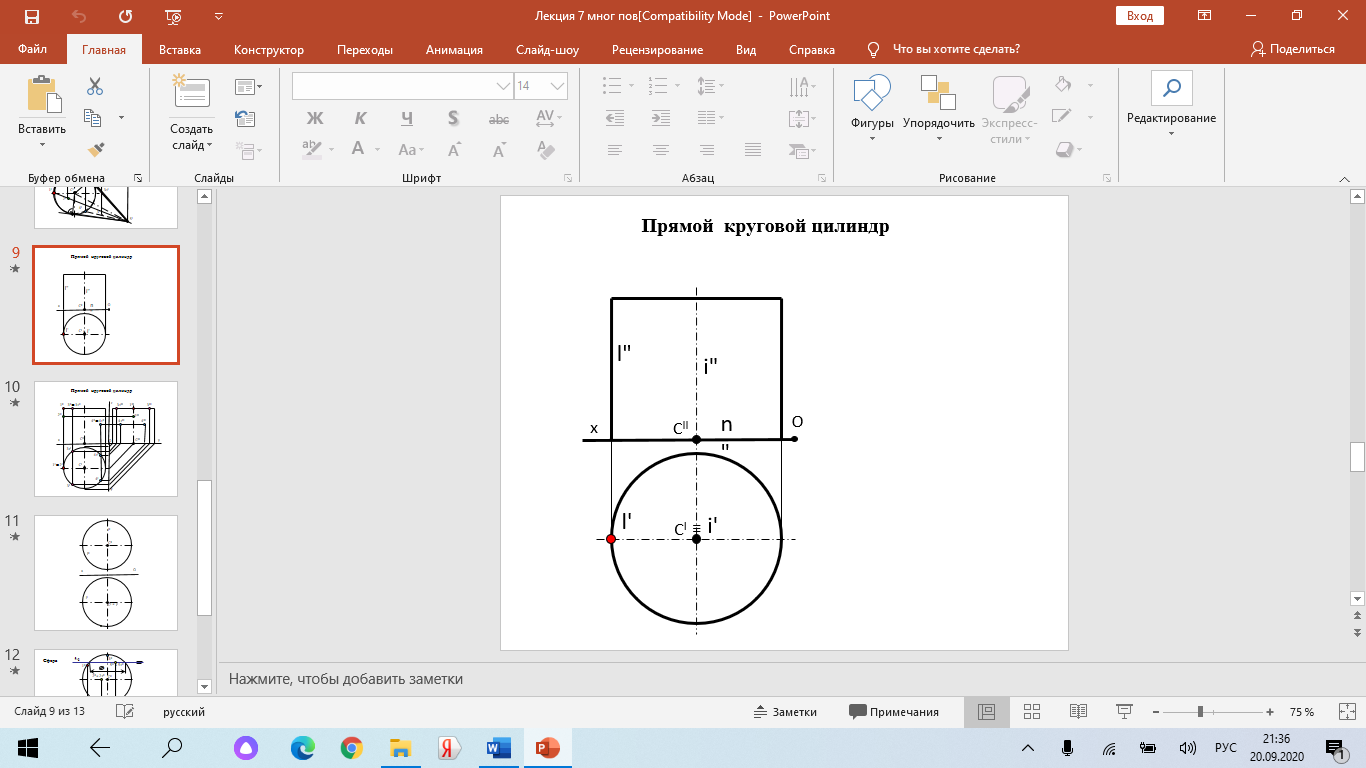  Сфера   Тор  Вырезы Построим линии вырезов в поверхностях несколькими проецирующими плоскостями в поверхностях. Любая линия или плоская фигура, расположенная в проецирующей плоскости, проецируется на плоскость проекций, которой она перпендикулярна, в прямую, совпадающую со следом плоскости Построить линию выреза в прямом круговом цилиндре проецирующими плоскостями в системе трёх плоскостей проекций.  Последовательность решения задачи: 1. Особенностью данной задачи является то, что обе секущие плоскости (,) - фронтально проецирующие, а поверхность прямого кругового цилиндра горизонтально проецирующая. Поэтому в задаче известны две проекции линии пересечения: на π1 они проецируются в окружность, а на π2 - в отрезки, соответствующие проекциям секущих плоскостей. Решение задачи сводится к построению профильной проекции линии пересечения по двум известным проекциям. 2. Построим линию пересечения плоскости с цилиндрической поверхностью. Плоскость является фронтально проецирующей, она пересекает цилиндр по плоской фигуре, ограниченной дугой эллипса. Дуга эллипса проецируется на π1 в дугу окружности, на π2 – в отрезок прямой, на π3 - в дугу эллипса. Линию пересечения построим по пяти характерным точкам (1,2,3,4,5) и двум вспомогательным (6,7). Построим фронтальные проекции этих точек. Для нахождения горизонтальной проекции точек опустим из 1//, 2//, 3//, 4//, 5//, 6//, 7// линии проекционной связи на горизонтальную проекцию поверхности цилиндра (окружность). Профильные проекции точек строим по линиям проекционной связи. Соединяем последовательно найденные проекции точек. 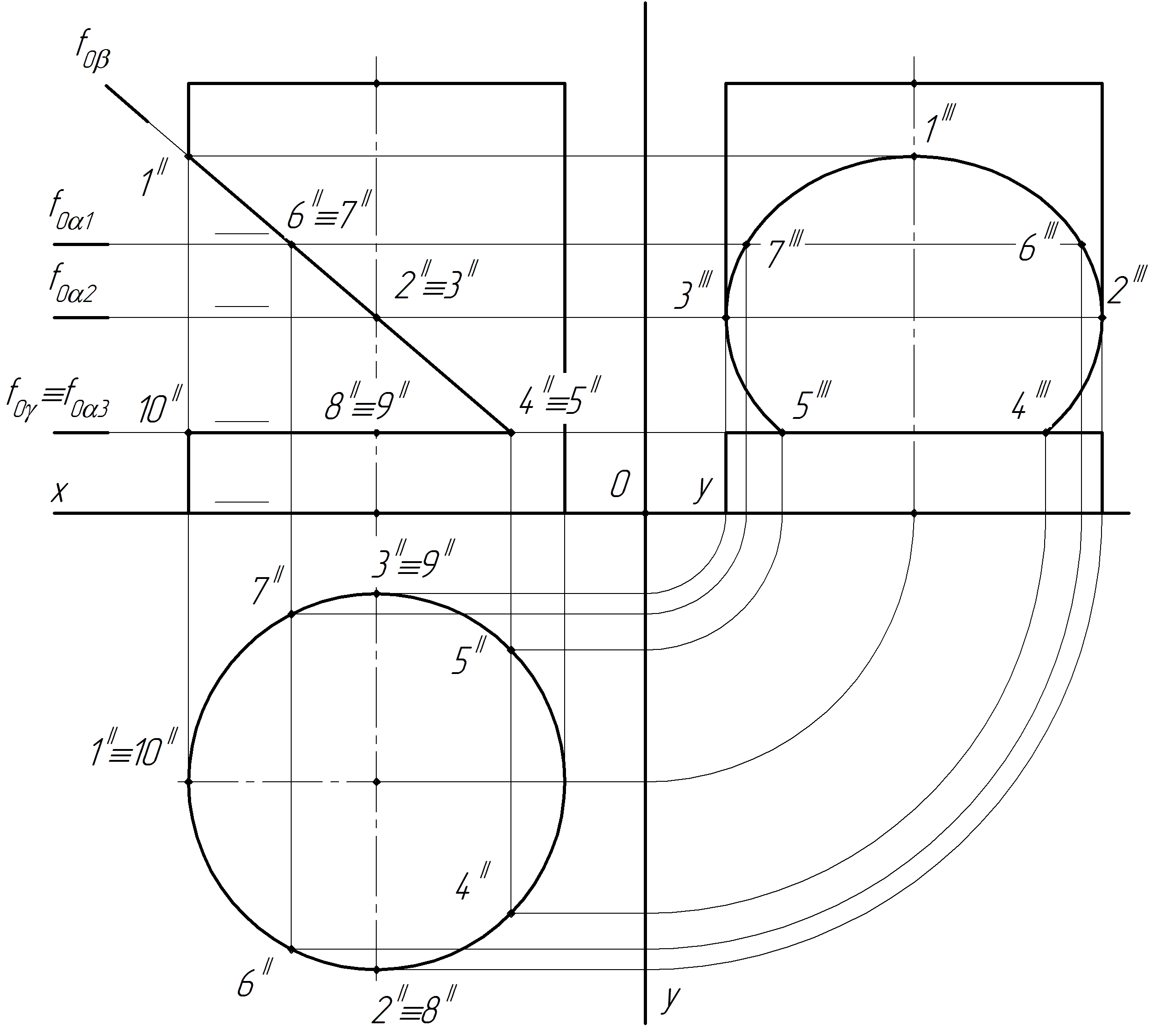 3. Горизонтальная плоскость расположена перпендикулярно оси цилиндра, следовательно, она пересечёт цилиндр по дуге окружности (4,5,8,9,10). Эта дуга проецируется на π1 в натуральную величину, а на π2 и π3 - в отрезки горизонтальной прямой. Отметим фронтальные проекции точек 8,9,10 на фронтальной проекции плоскости . Проведя линии проекционной связи, определяем их горизонтальные проекции 8/, 9/, 10/ на горизонтальной проекции поверхности цилиндра, профильные проекции точек (8///, 9///, 10///) строим по линиям проекционной связи. 4. Обводим видимый контур проекций цилиндра со сквозным вырезом сплошной основной линией (S мм), невидимые части выреза (4//, 5//) показываем штриховой линией (толщина линии S/3 – S/2 мм). Построить горизонтальную проекцию сквозного выреза в прямом круговом конусе. Плоскость, в зависимости от положения в пространстве, может пересекать конус по плоским фигурам ограниченным треугольником, окружностью, эллипсом, параболой, гиперболой или сочетанием данных линий. 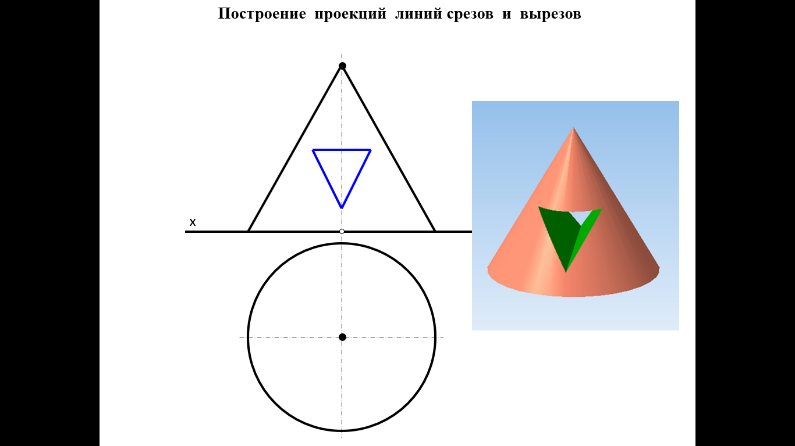 В задаче сквозной вырез образован тремя фронтально-проецирующими плоскостями , и δ. Последовательность решения задачи: 1. Плоскость является горизонтальной, перпендикулярной оси конуса. Она пересекает конус по плоской фигуре, ограниченной дугами окружности (1–3, 2–4). Эти дуги проецируются на π1 в натуральную величину. Горизонтальные проекции точек 1/, 2/, 3/, 4/ строим исходя из принадлежности их поверхности конуса. 2. Плоскости и δ не параллельны ни одной образующей конуса, следовательно, они пересекают конус по плоской фигуре ограниченной дугами эллипсов 1–5–9, 3–7–9, 2–6–10, 4–8–10. Фронтальные проекции (5//, 6//, 7//, 8//, 9//, 10//) точек отмечаем на фронтальных проекциях плоскостей. Горизонтальные проекции строим исходя из принадлежности их поверхности конуса. 3. Обводим видимый контур проекций конуса со сквозным вырезом сплошной основной линией. Строим линии пересечения плоскостей , и δ (1–2, 3–4, 9 – 10), учитываем их видимость.  Построить горизонтальную проекцию сквозного выреза на шаре.  Любая плоскость рассекает шар по кругу. Если секущая плоскость параллельна плоскости проекций, то круг проецируется на эту плоскость в натуральную величину, если нет – то в эллипс. Задан шар с вырезом образованным двумя фронтально-проецирующими плоскостями и . Построить вырезы на горизонтальной и фронтальной проекциях. 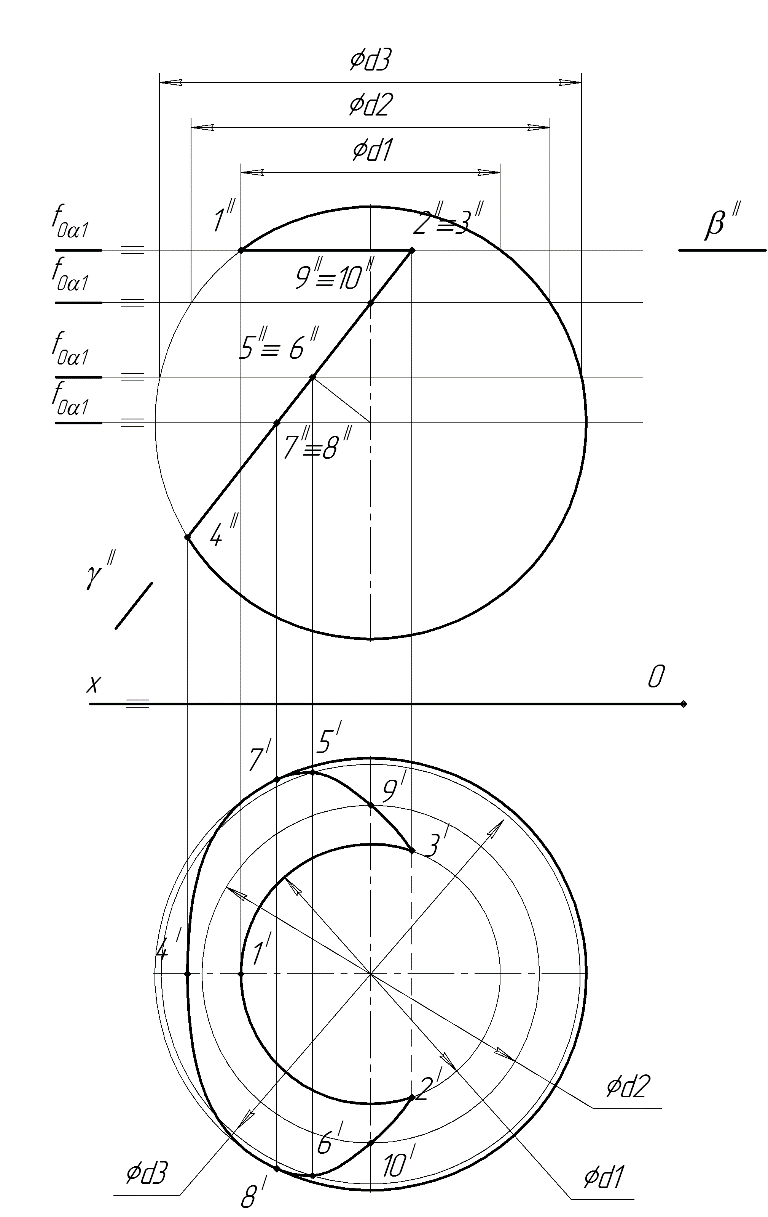 Последовательность решения задачи: 1. Плоскость является горизонтальной. Она пересекает шар по плоской фигуре, ограниченной дугой окружности (2–1–3). Эта дуга проецируются на π1 в натуральную величину. Горизонтальные проекции точек 1/, 2/, 3/ строим исходя из принадлежности их поверхности шара. 2. Плоскость не параллельна π1, следовательно, горизонтальная проекция сечения - плоская фигура, ограниченная дугой эллипса. Отмечаем на фронтальной проекции выреза следующие точки: 4 – точка малой оси эллипса сечения; 5,6 – большая ось эллипса сечения; 7,8 – характерные точки сечения, лежащие на экваторе сферы; 9,10 – дополнительные точки, характерные для профильной проекции. Горизонтальные проекции точек строим исходя из принадлежности их поверхности шара, применяя вспомогательные плоскости αi. 3. Обводим видимый контур проекций шара со сквозным вырезом сплошной основной линией. Строим линию пересечения плоскостей и (2/ – 3/), учитываем видимость. На эпюре в системе трех плоскостей проекций построить линии срезов и вырезов, заданных тел. Показать видимость. Решение задачи начинаем с построения по заданной фронтальной проекции тел горизонтальной и профильной проекций. Линии срезов и вырезов строим по алгоритмам, рассмотренным выше. 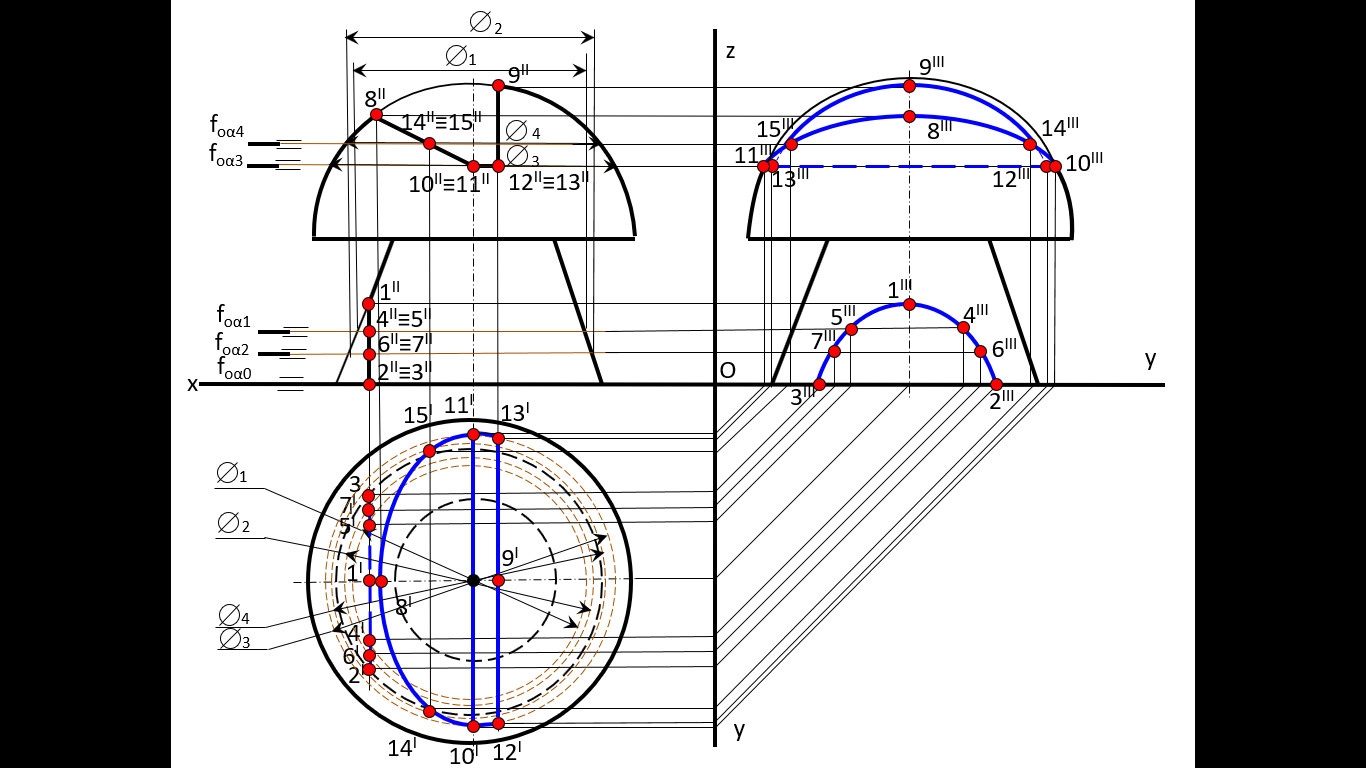 Способ замены плоскостей проекций Способ замены плоскостей проекций заключается в замене существующих плоскостей проекций новыми. Геометрические объекты при этом не меняют своего положения в пространстве. При выборе новой плоскости проекций сохраняется взаимная перпендикулярность плоскостей проекций.   Определить натуральную величину отрезка  Определить расстояние от точки S до плоскости ABC 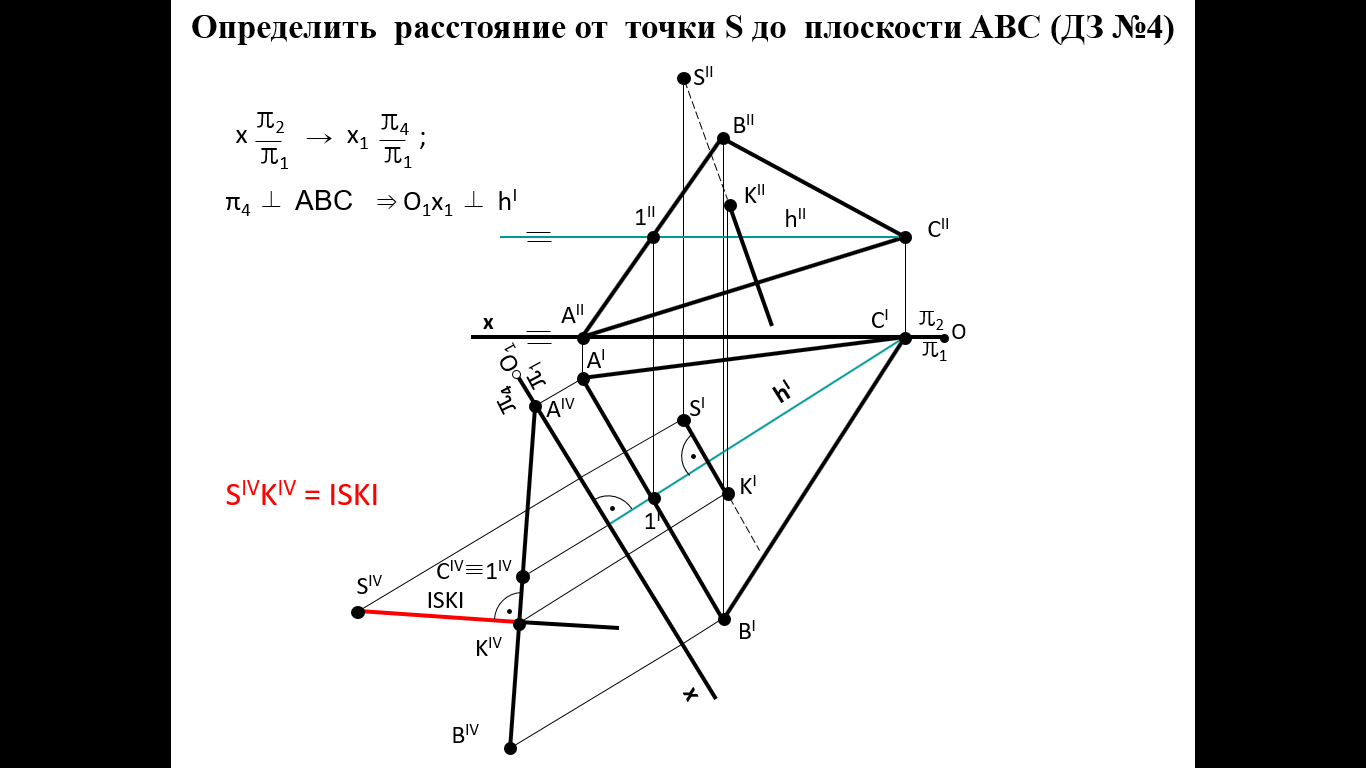 Двойная замена плоскостей проекций Алгоритм решения задач с применением двойной замены плоскостей проекций 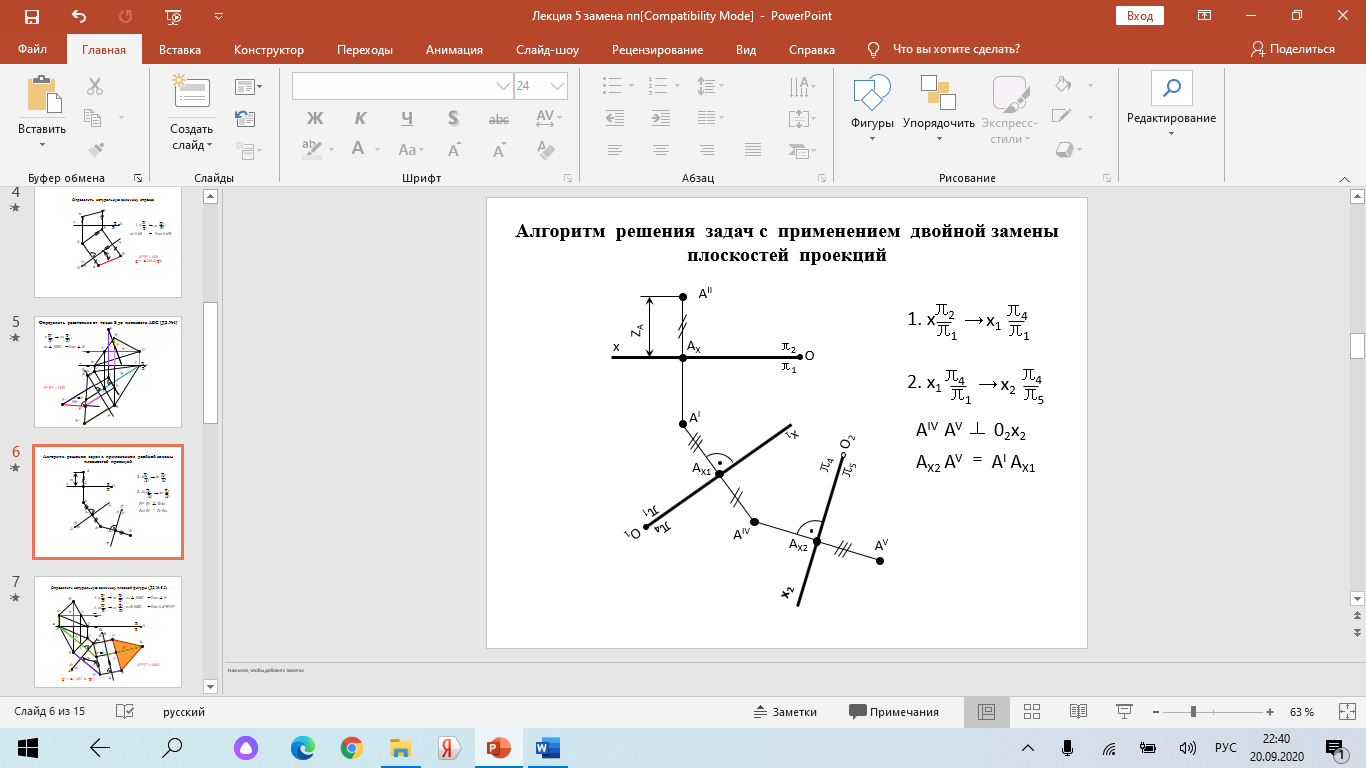 Определить натуральную величину плоской фигуры 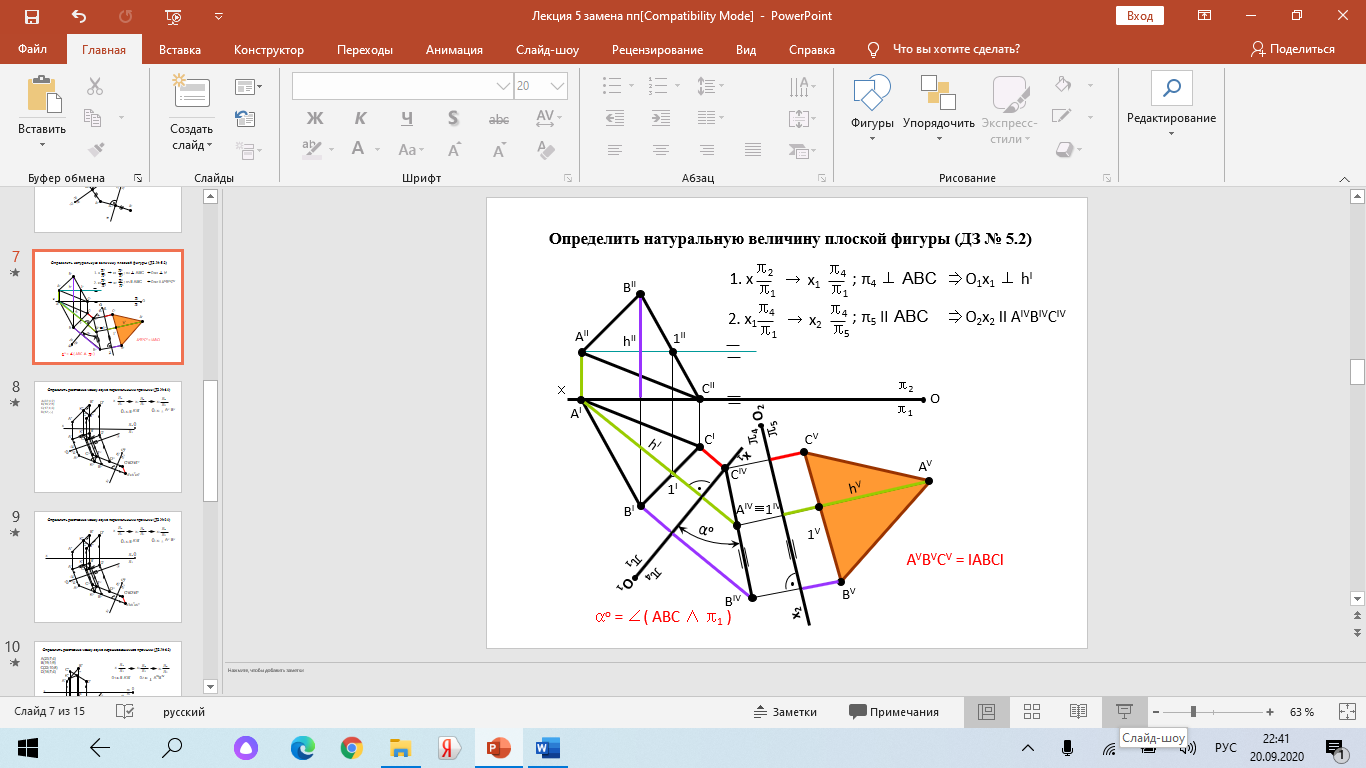 Определить расстояние между двумя параллельными прямыми 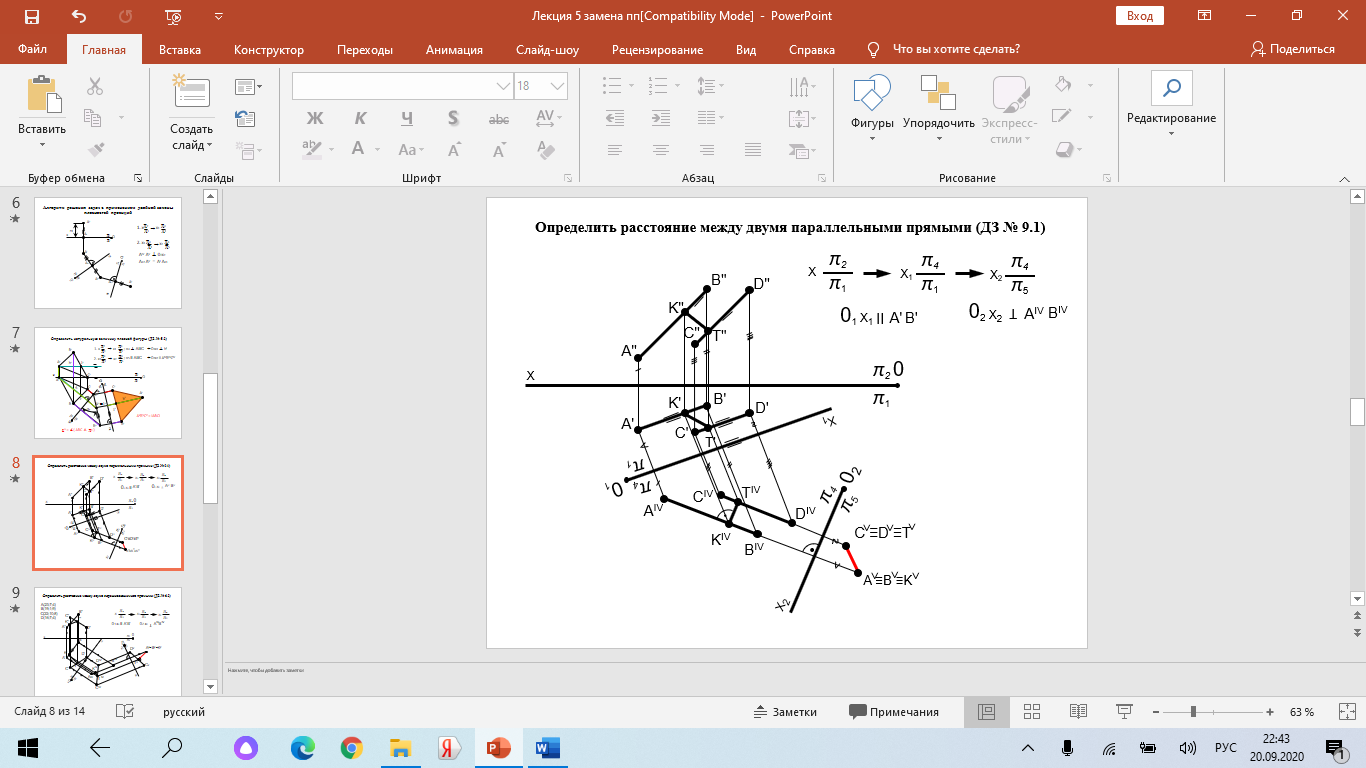 Определить расстояние между двумя скрещивающимися прямыми  Определить расстояние от точки до прямой 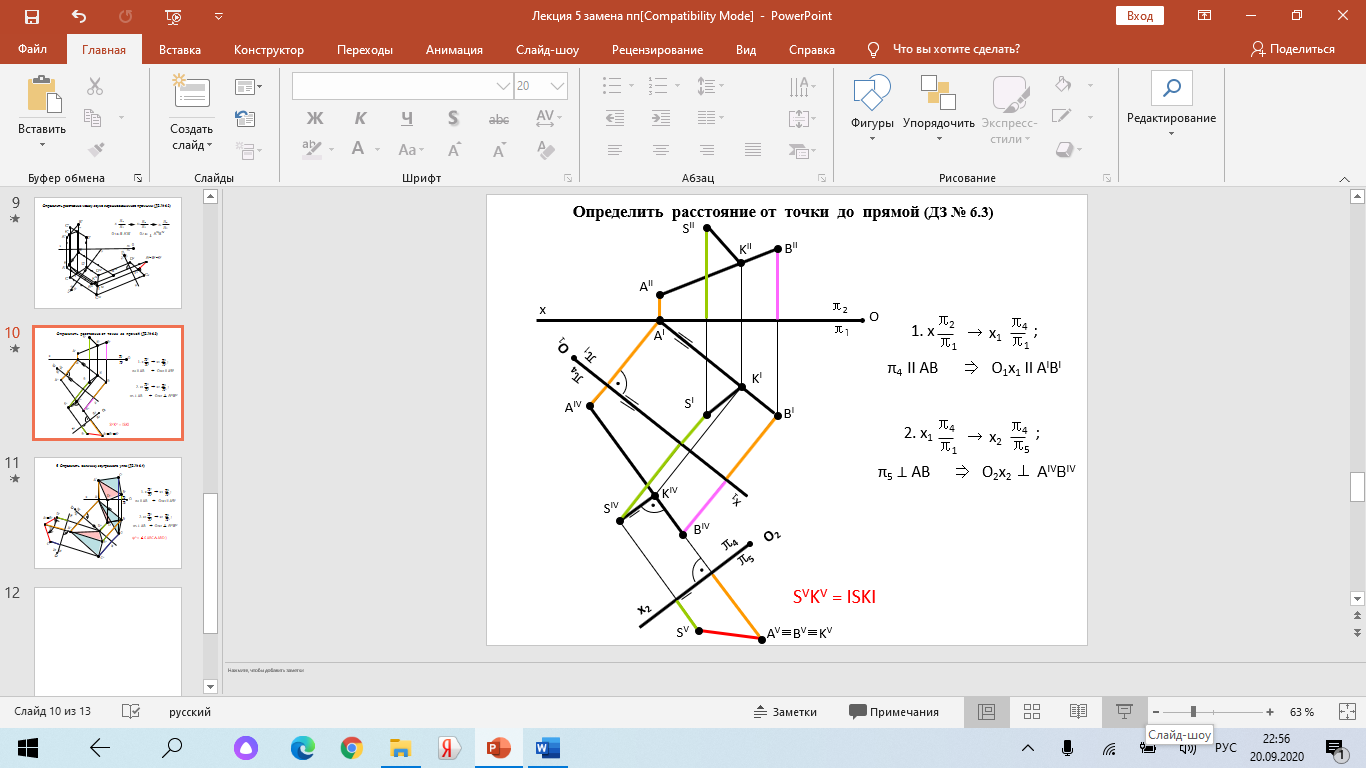 Определить величину двугранного угла  |
