Лекция. Лекция 20. Лекция 20 Основы динамики сооружений Учебные вопросы 20 Предмет и задачи динамики сооружений

• Название: Лекция 20 Основы динамики сооружений Учебные вопросы 20 Предмет и задачи динамики сооружений
• Анкор: Лекция
• Дата: 18.09.2021
• Размер: 0.5 Mb.
• Имя файла: Лекция 20.doc
• Тип: Лекция; #233757
• страница: 1 из 3

Лекция 20

Основы динамики сооружений
Учебные вопросы:

20.1. Предмет и задачи динамики сооружений

20.2. Системы с одной степенью свободы

20.3. Пример расчета балки в виде системы с одной степенью свободы

20.4. Свободные колебания системы с произвольнымчислом степеней свободы


Динамика сооружений - это один из специальных разделов строительной механики, посвященный методам расчета сооружений на динамические нагрузки. Динамические нагрузки по своей природе весьма разнообразны. К такого рода воздействиям относятся природные явления, т.е. сейсмические толчки, ветровые порывы, а также различные динамические воздействия технологического или аварийного происхождения: движение неуравновешенных частей машин и механизмов; падение летящего тела при соударение его с элементами конструкций; работа копров, молотов и других ударных механизмов; движение поездов, кранов и т.д.

Особенностью динамических нагрузок является то, что при их действии сооружение переходит в состояние движения, причем при периодическом повторении динамических воздействий в определенных условиях происходит накопление энергии системы, выра­жающееся в постепенном увеличении амплитуды колебаний.

Это явление, называемое резонансом, особенно опасно для сооружения тем, что разрушение может произойти и при воздействиях с малой интенсивностью.

Существенным отличием динамических методов расчета от статических является введение в уравнениях состояния нового пере­менного - времени и, ввиду их значительности, инерционных сил. При этом, если при решении аналогичных задач при статическом нагружении, уравнения состояния выражались при помощи алгебраических или трансцендентных уравнений, то соответствующая динамическая задача требует уже решения дифференциальных уравнений с производными по времени.

В динамике сооружений следует различать два типа движения или колебания системы. Колебания системы при отсутствии действия внешних сил называются свободными. Если колебания системы сопровождаются действием внешних динамических нагрузок, то колебания называются вынужденными.

Для описания динамических колебаний необходимо ввести в рассмотрение следующие понятия: круговая частота w и пе­риод колебаний . Круговая частота определяет число циклов колебания в течении  секунд, а период определяет интервал времени, в течении которого совершается полный цикл колебаний.

Системы в динамике сооружений различаются по числу степеней свободы. Числом степеней свободы системы называется число независимых геометрических параметров (обобщенных координат), определяющих положение системы (материальных точек) в любой момент времени при ее (их) движении. Число степеней свободы системы складывается из числа степеней свободы материальных точек, принадлежащих системе. Число степеней свободы является основной характеристикой системы при динамических воздействиях.

В динамике сооружений различают два основных подхода: кинетостатический и энергетический.

Кинетостатический подход состоит в том, что сооружение в произвольный момент времени предполагается находящимся в равновесном состоянии под действием заданных динамических и вызванных ими инерционных нагрузок. Далее для составления уравнений состояния применяются классические методы строительной механики (метод сил, перемещений или смешанный).

Энергетический подход основан в определении в равновесном состоянии через закон сохранения энергии с учетом инерционных сил. В частности, когда силы сопротивления движению не учитываются, энергетический принцип в общем случае записы­вается в виде:

,

где K - кинетическая энергия системы; V - потенциальная энергии системы или работа внешних или внутренних сил, так как система в процессе колебания находится в равновесном состоянии.

В настоящей книге при решении конкретных задач ограничимся применением кинетостатического подхода, а для вывода уравнения - метода сил.
20.2. Системы с одной степенью свободы

Рассмотрим систему в виде невесомой балки с сосредоточенной массой m, горизонтальным перемещением и поворотом которого будем пренебрегать. При таких предпосылках единственная материальная точка, т.е. сосредоточенная масса величиной m может совершать перемещения только в вертикальном направлении, следовательно, система имеет одну степень свободы.



Рис.20.1

Будем исследовать дви­жение системы из ее исходного положения равновесия при t= 0 (рис.20.1, а), считая перемещение вниз положительным.

Пусть на балку действует динамическая сила величиной: , где  - частота вынуждающей силы. Обозначая дополни­тельное перемещение мас­сы m от динамических на­грузок через y(t), вводим следующие начальные условия:

; . (20.1)

В процессе движения на массу действует сила инерции и сила сопротивления по Фойхту . Сила сопротивления движению возникает от различных внешних и внутренних причин: сопротивление движению внешней среды, трение в местах соединения элементов и опорных частях, внутреннее неупругое сопротивление материалов конструкций и т.д.

Заметим, что система, обладающая свойствами внутреннего сопротивления называется консервативной, а система, лишенная данного свойства - неконсервативной.

Вводим следующие обозначения:  - вертикальное перемещение балки в точке закрепления массы m от действия вертикальной единичной силы Р = 1, приложенной в той же точке;  - вертикальное перемещение балки в точке закрепления массы m от динамической силы , при этом: ;  - вертикальное перемещение балки в точке закрепления массы от действия вертикальной единичной силы Р = 1, приложенной в точке приложения внешней силы при ее отсутствии.

Применяя метод суперпозиции, очевидно, что, в произвольный момент времени полное перемещение сосредоточенной массы m принимает значение:

, (20.2)

откуда и определяется дифференциальное уравнение движения рассматриваемой системы:

. (20.3)

Принимаем обозначения: - круговая частота соб­ственных колебаний системы; - коэффициент затухания.

С учетом введенных обозначений, уравнение движения системы (14.3) принимает вид:

. (20.4)

Решение дифференциального уравнения (20.4), с учетом начальных условий (20.1) и, учитывая, что для реальных конструкций всегда выполняется , записывается в виде:

. (20.5)

Здесь приняты следующие обозначения:

; ; . (20.6)

Круговая частота называется круговой частотой собственных колебаний системы с учетом сил затухания.

Коэффициент затухания колебания определяется по корректированной гипотезе Фойхта, позволяющей получить наиболее обоснованные результаты для учета диссипации энергии в системе в процессе колебаний, т.е.:

, (20.7)

где  - называется логарифмическим декрементом затухания и определяется через отношения соседних амплитуд колебания, возникающих через промежуток времени :

. (20.8)

Для различных конструкций средние значения приводятся в таблице 20.1.
Таблица 20.1

Наименование конструкции
Стальные мосты Железобетонные мосты Железобетонные балки Железобетонные рамы Железобетонные ребристые перекрытия	0,17 0,63 0,56 0,25 0,57

Выражение (20.5) определяет перемещение сосредоточенной массы при действии силы , изменяющейся во времени по произвольному закону. Первый член выражения характеризует собственные колебания системы, а второй, интегральный член - вынужденные колебания.

Так как , то решение (20.5) преобразуется и принимает вид:

. (20.9)

Здесь приняты следующие обозначения:

; ; . (20.10)

Если в момент времени t = 0 система находится в состоянии покоя, т.е. , то решение (20.9) с учетом (20.10) преобразуется в виде:

.

Величина k_Д называется коэффициентом динамичности и характеризует эффект от динамической нагрузки по отношению к аналогичной статической нагрузке величиной P(t) = P₀ = const.

Коэффициент динамичности существенно зависит от отношения . При коэффициент динамичности стремится принять максимальное значение и колебания системы при называются резонансными, а амплитуда колебаний принимает опасное значение:

.
20.3. Пример расчета балки в виде системы с одной степенью свободы
Проверить прочность балки в рабочем режиме вибратора, расположенного по середине пролета балки (рис.20.2, а), учитывая только вертикальную составляющую вертикальной силы: , принимая: G = 15 кН - вес вибратора; Р₀ = P_a = 3 кН - вес не­уравновешенных частей вибра­тора; e = 0,01 м - эксцентриситет относительно оси вращения неуравновешенных частей; = 30 с^-1 - круговая частота внешней силы; l = 4 м - пролет балки. Поперечное сечение балки выполнено из двутавра №20, материал Ст3. Следовательно, Е=2,1×10⁸ кН/м² - модуль деформации материалов; J_x =1,84×10^-5 м⁴ - момент инер­ции; W_x = 1,84×10^-4 м³ - момент сопротивления поперечного сечения; R = 25×10⁴ кН/м² - расчетное сопротивление;  = 0,1 - логарифмический декремент. Интенсивность распределенных нагрузок принимается равной: q = 4 кН/м.

На первом этапе для выполнения расчетов необходимо определить величину коэффициента динамичности. Для этого сначала определим величину коэффициента затухания .

Воспользуемся эпюрой моментов, изображенной на рис.20.2, б и по формуле Мора определим :

.

Круговая частота собственных колебаний без учета затуханий: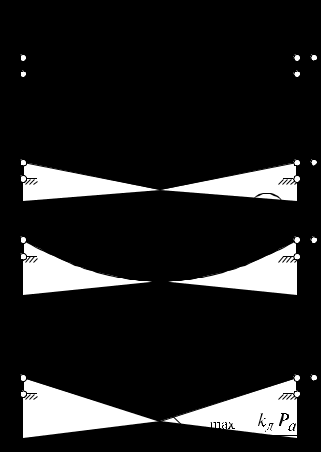

c^-1.


Рис.20.2

Собственная частота системы с учетом затухания колебания принимает значения:

 c^-1.

Коэффициент динамичности определяется из (14.10) по формуле:



.

Последовательно определим максимальное значение момента в опасном сечении (рис.20.2, в, г) от статических и динамических сил:

кН×м;

кН×м.

Максимальное напряжение в опасном сечении принимает значение:

кН/м²,

т.е. прочность конструкций обеспечена.
20.4. Свободные колебания системы с произвольнымчислом степеней свободы
Рассмотрим свободные колебания системы с конечным числом степеней свободы. В качестве объекта рассмотрим упругую невесо­мую балку, изображенную на рис.14.3 и с n сосредоточенными мас­сами m₁, m₂, m₃,..., m_n. Пренебрегаем продольными деформация­ми оси балки в процессе колебаний. При этом положение системы однозначно определяется перемещениями сосредоточенных масс y_i (t) (i = 1,2,3,...,n) в произвольные моменты времени t, вызван­ными упругими деформациями балки в поперечном направлении.