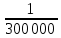универ. Геодезия. Лекция 1. Лекция по теме 1 Общие сведения о геодезии Лектор доцент Максимова М. В
 Скачать 335.36 Kb. Скачать 335.36 Kb.
|
|
Московский Государственный Университет Геодезии и картографии (МИИГАиК)  Кафедра Прикладной геодезии Дисциплина «Геодезия» Лекция по теме №1 «Общие сведения о геодезии» Лектор: доцент Максимова М.В. Москва, 2018 г. ОглавлениеОглавление 2 1. Геодезия, ее научные и практические задачи и роль в государстве 3 2. Краткая историческая справка о развитии геодезии 5 3. Понятие о форме и размерах Земли, поверхности относимости 7 4. Определение положения точек земной поверхности. Системы координат, применяемые в геодезии 9 5. Проектирование точек, малых участков земной поверхности на горизонтальную плоскость. Измеряемые в геодезии величины. Единицы мер, применяемые в геодезии 13 6. Изображение земной поверхности на сфере и на плоскости. Влияние кривизны Земли на горизонтальные расстояния и на высоты точек. Понятие о плане, карте, профиле местности. Аэрофотоснимок 16 1. Геодезия, ее научные и практические задачи и роль в государствеГеодезия в переводе с греческого языка означает «землеразделение». Как одна из наук о Земле геодезия возникла в далекой древности из практических потребностей человека. Это наука об измерениях на земной поверхности, о методах изображения поверхности земли на планах и картах и о методах определения фигуры и размеров Земли. Появление лазерного излучения, бурное развитие микроэлектроники и автоматики во второй половине XX в. привели к повсеместному внедрению в науку и практику ЭВМ и информационных систем. Ускоренное развитие получила информатика. В геодезии в последнее время широко внедряются ГНСС- и ГИС-технологии, как наиболее эффективные современные технологические процессы. Системы спутникового позиционирования (GPS и ГЛОНАСС) - специальные приемники и антенны для приема сигналов от спутников. Они обеспечивают автономное определение координат точек земной поверхности с геодезической точностью. ГИС-технологии - это программное обеспечение, современные высокие технологии и аппаратные средства (электронные тахеометры и регистраторы), применяемые для ввода и вывода пространственной информации в геодезических, географических, геофизических, геологических и других целях. Современная геодезия решает целый ряд научных и практических задач и делится на несколько самостоятельных дисциплин. Определение формы и размеров Земли и создание государственных опорных сетей составляет предметвысшей геодезии. Построением сетей сгущения и изображением местности на планах и картах занимается топография или геодезия. Прикладная геодезия решает геодезические задачи при изысканиях, строительстве и эксплуатации инженерных сооружений. Разработкой и изучением методов и процессов создания карт на обширные территории, всю поверхность Земли и поверхности других планет занимается картография. Развитие фотографии и авиации способствовало съемке земной поверхности с самолета и развитию аэрофотосъемкии фотограмметрии. С запуском искусственных спутников Земли, других космических летательных аппаратов, с изучением шельфа океанов и морей появились новые ветви геодезии: космическая геодезия, исследование природных ресурсов аэрокосмическими методами, морская геодезия. В наши дни в России возникла острая потребность в специалистах по геодезии для составления и ведения государственного кадастра, появляются новые разделы и дисциплины науки геодезии. Геодезия развивается в тесной связи и на основе других наук. Математика вооружает геодезию средствами анализа и методами обработки результатов измерений. На основе законов физики создаются оптико-механические, оптико-электронные и лазерные геодезические приборы. Астрономия обеспечивает геодезию необходимыми исходными данными. Знание географии и геоморфологии помогает более полно и правильно отобразить на картах земную поверхность (ее неровности, растительный покров, реки, озера и т. д.) и результаты деятельности людей (населенные пункты, дороги, промышленные предприятия и другие сооружения). Для графического оформления планов и карт топографам и геодезистам необходимы знания, приемы и навыки топографического черчения. Результаты геодезических измерений и прежде всего планы и карты широко используются в промышленности и на транспорте, в сельском и лесном хозяйствах, при геологической разведке и разработке месторождений полезных ископаемых, планировке и застройке городов, в науке и обороне страны. Трудно переоценить роль точных геодезических наблюдений и измерений в современных высоких технологиях и технологиях будущего, в предсказаниях землетрясений в сейсмоактивных регионах и в экологии. 2. Краткая историческая справка о развитии геодезииИзвестно, что геодезические измерения на местности в Китае, Греции, Индии, Вавилонии производились еще в ХХ-Х вв. до н. э. В Древнем Египте в ХХ-ІХ вв. до н. э. при сооружении каналов применяли нивелирование. В Греции Аристотель в IV в. до н.э. определил название науки об измерениях на поверхности Земли – геодезия. Эратосфен (III в. до н. э.) впервые вычислил размеры земного шара из градусных измерений. Александрийский астроном Гиппарх во II в. до н.э. изобрел астролябию (угломерный прибор) и ввел в употребление понятие «географические координаты». По знаменитым сочинениям Герона (II в. до н.э.) «Измерения», «О диоптре» известно о высоком уровне геодезических знаний того времени. Достоверных данных о развитии геодезии в первом тысячелетии нашей эры нет. Во второй половине второго тысячелетия в Европе в связи с оживлением торговых связей, расширением пространств мореплавания развиваются геодезические и картографические работы как следствие открытий в области математики, физики, точной механики и оптики. К этому периоду относятся изобретения зрительной трубы, микроскопа, верньера, уровней и т. д. Первые сведения о геодезических измерениях в России относятся к XI в., когда между Керчью и Таманью по льду была измерена ширина Керченского пролива. Первой русской картой является карта Московского государства «Большой Чертеж», созданная в XVI в. Первая карта Сибири составлена в 1667 г. при Тобольском воеводстве. С укреплением государства Российского при Петре I, в начале XVIII в., открыты Навигацкая школа в Москве и Морская академия в Петербурге, из стен которых вышли первые русские геодезисты, топографы и астрономы; с 1779 г. их подготовка началась в Константиновском Межевом институте (ныне Московский государственный университет геодезии и картографии (МИИГАиК)). Со времени организации в России Корпуса военных топографов (1822) съемочные работы стали ускоренно развиваться. На рубеже ХVІІІ-ХІХ вв. и в первой половике XIX в. выполнены знаменитые градусные измерения: Большое французское и Дуга Струве в России. Измерение В.Я. Струве - К. П. Теннера общей протяженностью 3000 км (25°20') от Северного Ледовитого океана до устья Дуная с ошибкой всего 12 м остается образцом работ тех лет. В XIX в. в геодезии был разработан способ математической обработки результатов астрономических и геодезических измерений - метод наименьших квадратов, предложенный А. Лежандром в 1806 г. и обоснованный в 1808-1810 гг. К. Ф. Гауссом. В последующие годы русские ученые П. А. Чебышев, А. А. Марков, А. М. Ляпунов и другие развили этот метод. Геодезические и съемочные работы в советский период базировались на результатах исследований, проведенных геодезистами под руководством Ф. Н. Красовского. В 1928 г. был открыт Центральный научно-исследовательский институт геодезии, аэросъемки и картографии (ЦНИИГАиК). В 1940 г. по результатам отечественных измерений определены фигура и размеры эллипсоида Красовского (Ф. Н. Красовский, А. А. Изотов). М. С. Молоденским разработана новая теория изучения фигуры Земли и ее внешнего гравитационного поля. Созданы отечественные научные школы аэрофотогеодезии и прикладной геодезии. В 60-х годах были образованы Новосибирский институт прикладной геодезии (НИИПГ) и Государственный научно-производственный центр «Природа» (Госцентр «Природа»). К середине 60-х годов на всю территорию страны была создана Государственная астрономо-геодезическая сеть высокой точности. В середине 50-х годов - карта масштаба 1: 100 000, к концу 80-х годов - карта масштаба 1: 25 000, новые генпланы более чем 2100 городов в масштабах 1: 5000 и 1: 2000. К 90-м годам более 50% территории СССР было покрыто съемками в масштабах 1: 10 000, 1: 5000, 1: 2000 и крупнее. С 1965 г. начаты и велись в больших объемах работы по съемке шельфа морей и океанов. Контроль и общее руководство за выполнением всех топографо-геодезических работ в СССР осуществляло Главное управление геодезии и картографии при Совете Министров СССР (ГУГК). 3. Понятие о форме и размерах Земли, поверхности относимостиНеобходимость знания фигуры и размеров Земли возникла в связи с потребностями мореплавания. В наши дни требуются более точные данные о размерах Земли. В истории вопроса о фигуре Земли различают три периода. До конца XVII в. Землю принимали за шар. Последующие 150 лет, когда И. Ньютон обосновал, что Земля сплюснута у полюсов, ее стали считать сфероидом (фигура равновесия вращающейся вязкой массы). В 1735 г. Французская академия наук снарядила две экспедиции для выполнения градусных измерений в Перу (ближе к экватору) и Лапландию (ближе к Северному полюсу), которые подтвердили выводы И. Ньютона. Последние 150 лет - современный период - наука пришла к выводу, что сфероид - это лишь второе приближение к истинной фигуре Земли. Землю стали считать, по определению немецкого физика Листинга, геоидом (в переводе с греческого «гео» - земля, «эйдос» - вид) - телом, имеющим неправильную математическую фигуру. Геоид - фигура Земли, ограниченная уровенной поверхностью, совпадающей со средней уровенной поверхностью воды в открытых морях и океанах, мысленно продолженной под материками так, что для всех точек земной поверхности она перпендикулярна отвесным линиям, проходящим через эти точки. Поверхность геоида - сложная поверхность, связанная с плотностью и распределением масс внутри Земли (рис. 1). Для целей практической геодезии достаточно Землю принять за простейший из сфероидов - эллипсоид вращения - фигуру, образованную вращением эллипса вокруг его малой оси. До второй половины XX в. в разных странах принимались разные размеры земных эллипсоидов. Это объяснялось не только недостаточной изученностью формы и размеров Земли, но и, главным образом, исторически сложившейся практикой топографо-геодезических работ в разных странах. В 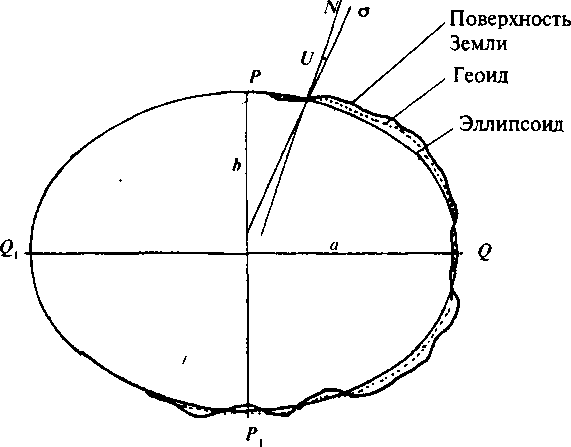 Германии с 1841 г. принят эллипсоид Бесселя (большая полуось эллипса а = 6 377 397 м; сжатие α = 1/299, 2). До 1946 г. эллипсоид Бесселя принимался и в России (СССР), с 1946 г. принят эллипсоид Красовского (а = 6 378 245 м; α = 1/298, 3). В США с 1909 г. - эллипсоид Хейфорда (а = 6 378 388 м; α = 1/297, 0). Рис. 1. Геоид. Эллипсоид. Поверхность Земли: σ - отвесная линия; Ν - нормаль к эллипсоиду; U - уклонение отвеса. Единые общепринятые размеры земного эллипсоида впервые учреждены XVI ассамблеей Международного геодезического и геофизического союза (Франция, Гренобль, 1975 г.): большая полуось а = 6 378 140 ± 5м (рис. 1); сжатие (α = (а-b) /а) α = 1/298, 257. В последующие годы размеры земного эллипсоида уточнялись: в 1983 г. – а = 6 378 137 ± 1 м, α = 1/298, 256; в 1987 г. – а = 6 378 136 ± 1 м, α= 1/298, 256. Чтобы земной эллипсоид ближе подходил к геоиду, его соответственно располагают в теле Земли или, как говорят, ориентируют. Эллипсоид, с определенными размерами и определенным образом ориентированный в теле Земли, называется референц-эллипсоидом. Поверхность референц-эллипсоида является той поверхностью, на которую проектируют (относят) все измерения, выполненные на физической поверхности Земли. Такая поверхность называется поверхностью относимости. Во многих случаях практики геодезических работ достаточно считать, что поверхность относимости (поверхность референц-эллипсоида) совпадает с поверхностью геоида (с уровенной поверхностью) и ее можно принять за поверхность шара, равновеликого по объему с земным эллипсоидом. Например, для эллипсоида Красовского радиус такого шара R = 6371,11 км. 4. Определение положения точек земной поверхности. Системы координат, применяемые в геодезииПоложение любой точки земной поверхности определяется однозначно, если известны ее координаты и высота. В геодезии, как правило, применяются геодезические, астрономическиеипрямоугольные координаты. В геодезической системе координат основной координатной поверхностью считают поверхность референц-эллипсоида. Проектирование точек физической поверхности Земли на эту поверхность выполняется по нормалям. Основными координатными линиями являются геодезические меридианы и параллели. Плоскостью геодезического меридиана называют сечение эллипсоида плоскостью, проходящей через малую (полярную) ось. Плоскостью геодезической параллели называют плоскость сечения эллипсоида, перпендикулярную полярной оси. Положение точки на эллипсоиде определяется пересечением меридиана и параллели, которое задается соответственно долготой и широтой. Г  еодезичекая широта В - угол от плоскости экватора до нормали N к поверхности эллипсоида в данной точке М (рис. 2). Широта изменяется от 0 до 90°, к северу - северная, к югу - южная. Геодезическая долгота L - угол между плоскостью начального меридиана (Гринвичского) и плоскостью меридиана данной точки М. Долгота изменяется от 0 до 180°, к востоку - восточная, к западу - западная. Геодезический азимут А - угол в плоскости, перпендикулярной нормали, от северного направления меридиана в данной точке до направления данной линии MD, измеренный по ходу часовой стрелки. Азимут изменяется от 0 до 360°. Рис. 2. Геодезические координаты. Азимут: М - произвольная точка земной поверхности; PP' - малая ось эллипсоида (полярная ось); PQP' - Гринвичский меридиан (начальный меридиан); В - геодезическая широта точки М; L - геодезическая долгота точки М, А- геодезический азимут линии MD, ΝΜ - нормаль к поверхности эллипсоида в точке М; σМ - отвесная линия в точке М; QM0Q' - экватор; О - центр эллипсоида; U- уклонение отвесной линии. Астрономические широта φ, долгота λ и азимут а определяются аналогично геодезическим, но относятся они к отвесной линии σМ в данной точке. Отвесная линия зависит от распределения и плотности масс внутри Земли и всегда совпадает с направлением силы тяжести в данной точке. Угол U, образованный нормалью и отвесной линией в данной точке, называется уклонением отвесной линии. Величина угла U на территории бывшего СССР не превышает 1' и в практике массовых инженерно-геодезических работ может не учитываться. Тогда, принимая Землю за шар и не учитывая уклонение отвеса, геодезические и астрономические координаты будут равны между собой. В этом случае они иногда называются географическими координатами. Д 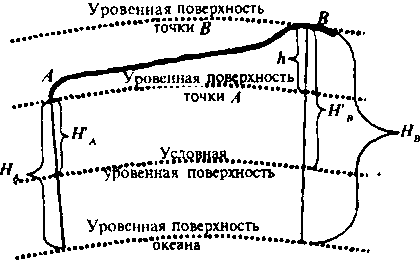 ля полного определения положения точки на земной поверхности необходимо, кроме плановых координат, знать высоты Н точек. В зависимости от выбора начала отсчета высот различают: абсолютные высоты, или альтитуды, и относительные, или условные, высоты. За начало отсчета абсолютных высот принимают средний уровень океана (рис. 3). Числовые значения высот в геодезии называются отметками. Рис. 3. Высоты точек: НА, НВ- абсолютные высоты точек: Н'A, Н'B - относительные высоты; А - превышение между точками А и В. Могут применяться и другие системы координат. Например, система прямоугольных пространственных координат X, Υ, Ζ с началом в центре земного эллипсоида. Оси X и Υ располагаются в плоскости экватора, первая - в плоскости начального меридиана, вторая - ей перпендикулярно, ось Ζ - по земной оси. Такая система координат называется геоцентрической. На ограниченных участках земной поверхности, когда сферичностью Земли можно пренебречь, применяют систему плоских прямоугольных координат X, Υ. В отличие от математики (рис. 4,а), где принята левая система плоских прямоугольных координат с положительным направлением оси абсцисс X, совпадающим с направлением неподвижного радиуса (на восток), в геодезии принята правая система плоских прямоугольных координат (рис. 4,б) с положительным направлением оси X, совпадающим с северным направлением меридиана и направлением оси Y - на восток. Из рис. 4 очевидно, что тригонометрические функции углов и знаки координат в одноименных четвертях левой и правой систем совпадают. 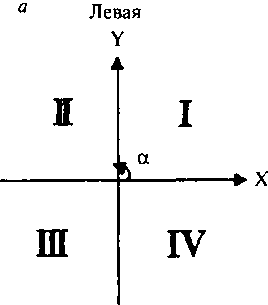 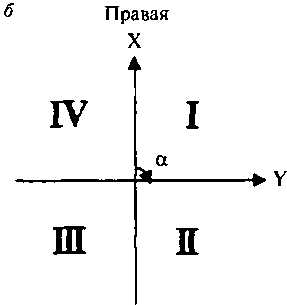 Рис. 4. Системы плоских прямоугольных координат, принятые в математике (а) и геодезии (б) Выбор правой системы координат в геодезии обусловлен удобством и простотой отыскания северного направления меридиана, от которого отсчитываются углы (по тени в полдень, по Полярной звезде, по Солнцу). 5. Проектирование точек, малых участков земной поверхности на горизонтальную плоскость. Измеряемые в геодезии величины. Единицы мер, применяемые в геодезииФизическая земная поверхность представляет собой сложные пространственные формы: горы, котловины, хребты, лощины и т. п. Равнинные участки встречаются редко. Прежде, чем изобразить участок поверхности Земли на плане или карте, необходимо предварительно все точки неровной поверхности спроектировать на уровенную поверхность, совпадающую с горизонтальной плоскостью для малых участков, и определить координаты и высоты этих точек. Такое проектирование точек поверхности Земли на горизонтальную плоскость в геодезии осуществляется ортогонально (перпендикулярно) по отвесным линиям. На рис. 5 показан малый участок поверхности Земли. 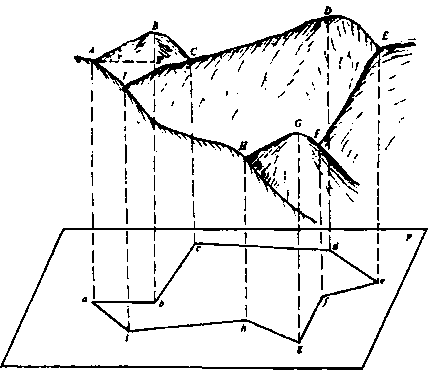 Рис. 5. Ортогональная проекция Точки пространственного многоугольника ABCDEFGHI требуется спроектировать ортогонально на горизонтальную плоскость Р*. Каждой точке земной поверхности будет соответствовать точка на горизонтальной плоскости. Так, точка а является горизонтальной проекцией точки А на местности, b - проекция точки В и т. д. Плоский многоугольник abcdefghi является горизонтальной проекцией пространственного многоугольника. Горизонтальная проекция ab = АВ' = ABcosv, где v - угол наклона (вертикальный угол) линии местности АВ. Проекция линии АВ на вертикальную плоскость ВВ' = ABsinv = h (превышение точки В над точкой А). Угол bаі является горизонтальной проекцией пространственного угла ВАІ. Итак, на местности измеряют длины наклонных линий АВ, ВС, CD и т.д., вертикальные и горизонтальные углы. Горизонтальную проекцию линии местности в геодезии называют горизонтальным проложением и обозначают буквой S. Таким образом, задача геодезических измерений на местности сводится к измерениям длин (наклонных, горизонтальных и вертикальных) и углов (горизонтальных и вертикальных) с последующим вычислением координат и высот точек. Единицы мер. Единицей линейных мер является международный метр - одна десятимиллионная часть четверти земного (Парижского) меридиана, хранимый в Париже. В России находятся два экземпляра копий этого метра (№ 11 и 28) из 32 имеющихся. Современное определение метра введено в 1960 г. Согласно ему, 1 м равен 1 650 763,73 длин волн оранжевого излучения светящегося газа криптона-86. Линейные меры 1 км (километр) = 1000, 000 м; 1 м (метр) = 1, 000 м; 1 дм (дециметр) = 0, 100 м; 1 см (сантиметр) = 0, 010 м; 1 мм (миллиметр) = 0, 001 м. По линейным мерам выводятся меры площадей и объемов: 1 км2 (квадратный километр) = 1 000 000, 000 000 м2 = = 100 га; 1 га (гектар) = 10 000, 000 000 м2; 1 м2 (квадратный метр) = 1, 000 000 м2; 1 дм2 (квадратный дециметр) = 0, 010 000 м2; 1 см2 (квадратный сантиметр) = 0, 000 100 м2; 1 мм2 (квадратный миллиметр) = 0, 000 001 м2. Единицей объема является 1 м3 (1 кубический метр). Угловые меры подразделяются на градусы и грады. Градус - девяностая часть прямого угла, град - сотая часть прямого угла: 1° = 1 градус = 1° 00'00" = 60' (минут); 1' = 1 минута = 0° 01'00" = 60" (секунд); 1" = 1 секунда = 0° 00' 01"; lg = 1 град = 1, 0000g = 100с (десятичных минут); 1c = 1 десятичная минута = 0, 0100g = 100сс (десятичных секунд); 1cc = 1 десятичная секунда = 0, 0001g. Полная окружность содержит 360°, или 400g. Между угловыми единицами имеются следующие соотношения: 1g = 0, 9°; 1°= 1, 111g; 1c = 0, 54'; 1' = 1, 851c; 1cc = 0, 324"; 1"= 3, 08641975cc. Перевод одних угловых мер в другие облегчается при использовании соответствующих таблиц. В современной литературе и практике вводятся новые угловые единицы: гон и миллигон: 1 гон = lg = 0,9°; 1 гон = 1000 мгон; 1 мгон = 0, 001 гон = 0, 1c = 10cc = 3, 2"= 0, 054'. Значения углов можно выражать в радианной мере. В таком случае соответствующий угол понимается как центральный угол окружности, а его величина выражается отношением длины соответствующей дуги к радиусу. Величине одной дуговой меры соответствует угол ρ (радиан), для которого длина дуги равна радиусу. Значения радиана: в шестидесятичной угловой мере ρ° = 180/π = 57,2958° = 57,3°; ρ' = 3437,75' = 3438'; ρ"= 206264,8" = 206265"; в десятичной угловой мере ρg = 200g/π = 63,6620g =63,7g; рс = 6366,20c ; ρcc = 636620cc. В геодезии также находят применение меры массы, температуры, времени, давления и частоты колебаний. Единицей массы является 1 кг (один килограмм), единицей температуры является 1°С (один градус по шкале Цельсия), единицей времени - 1 с (одна секунда), единицей давления - 1 Па (один паскаль). 100 Па = 1 гПа (один гектопаскаль) = 1 мбар (один миллибар) = 0,001 бар =  мм рт. ст. (0,750 062 мм рт. ст.). За единицу измерения частоты колебаний принят 1 Гц (один герц) - одно колебание в 1 с. 1 кГц (один килогерц) = = 1000 Гц, 1 МГц (один мегагерц) = 1000 кГц = 1 000 000 Гц. мм рт. ст. (0,750 062 мм рт. ст.). За единицу измерения частоты колебаний принят 1 Гц (один герц) - одно колебание в 1 с. 1 кГц (один килогерц) = = 1000 Гц, 1 МГц (один мегагерц) = 1000 кГц = 1 000 000 Гц.6. Изображение земной поверхности на сфере и на плоскости. Влияние кривизны Земли на горизонтальные расстояния и на высоты точек. Понятие о плане, карте, профиле местности. АэрофотоснимокИзобразить земную поверхность, казалось бы, естественным на сфере, например, на глобусе. Для этого достаточно нанести на поверхность глобуса сетку меридианов и параллелей и по координатам φ и λ нанести все контуры и предметы. Зная высоты, можно изобразить и неровности местности. Но изображение на глобусе не будет наглядным даже при значительных его размерах. Например, на глобусе радиусом в 1 м самая высокая гора Эверест над поверхностью такого глобуса обозначится песчинкой чуть больше 1 мм. К тому же изображение на сфере невозможно использовать для целей проектирования инженерных сооружений. Поэтому поверхность Земли изображают на плоскости. Установим искажение при замене дуги сферы отрезком касательной. Пусть на поверхности Земли, принятой за поверхность шара радиусом R, расположены произвольные точки А и В (рис. 6).  Рис. 6. К влиянию кривизны Земли Если заменить дугу S отрезком касательной t, то получим, ΔS = t - S, где ΔS - влияние кривизны Земли на горизонтальное расстояние. Докажем, что при S ≤ 10 км и R = 6371 км искажение ΔS является малой величиной и ею можно пренебречь. По построению t=Rtgε, (1) 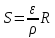 (2) (2)По малости угла ε (ε < 5’) 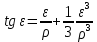 (3) (3)С учетом формул (1) - (3) имеем 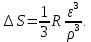 Принимая 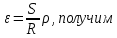 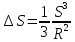 или в относительной мере 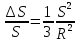 . .Для разных длин дуги S влияние кривизны ΔS в абсолютных и относительных величинах приведено в табл. 1. Таблица 1. К влиянию кривизны земли на расстояния
Замена дуги S ≤ 10 км отрезком касательной t не окажет заметного влияния на горизонтальные расстояния, так как ΔS/S≤1/1000000, что меньше погрешностей современных геодезических средств линейных измерений. Поэтому малые участки земной поверхности будут ортогонально изображаться на плоскости без заметных искажений. Такое уменьшенное и подобное ортогональное изображение на бумаге малого участка поверхности Земли называют планом. Но с увеличением расстояний искажение ΔS растет очень быстро, так как оно пропорционально 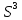 и уже при 20 км равно 7 см, при 100 км - 10 м и его необходимо учитывать. и уже при 20 км равно 7 см, при 100 км - 10 м и его необходимо учитывать.Большие участки или всю поверхность Земли нельзя изобразить на плоскости без искажений (без складок или разрывов). Задача состоит в том, чтобы определить их закономерности математически. Построенное по определенным математическим законам, уменьшенное и искаженное изображение части земной поверхности или всей поверхности Земли на бумаге называют картой. Для качественной и количественной характеристики неровностей местности по заданному направлению строят профиль местности. Уменьшенное изображение на бумаге вертикального профиля (разреза) местности называется профилем. При изображении земной поверхности широкое применение находят аэрофотоснимки. Аэрофотоснимок, в отличие от плана, не ортогональная, а центральная проекция участка местности (рис. 7). 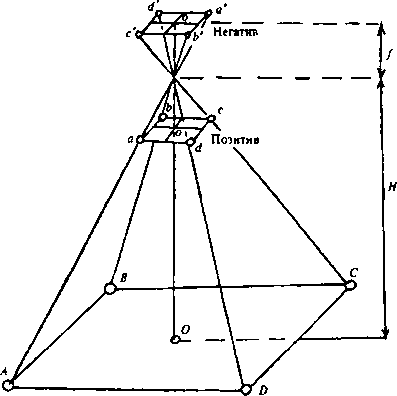 Рис. 7. Центральная проекция: f - фокусное расстояние камеры; H - высота фотографирования; 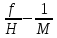 - масштаб аэрофотоснимка - масштаб аэрофотоснимкаРассмотрим далее влияние кривизны Земли на превышения и высоты точек. На рис. 6 ВВ' = Δh - ошибка за кривизну Земли в превышении или высоте точки определяется из соотношения (R+Δh)2 = R2 + t2. На основе вышесказанного, принимая S = t и отбрасывая (Δh)2 как величину второго порядка малости, получаем 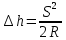 . .Соответственно вычислим Δh для разных S и занесем в таблицу 2 Таблица 2. К влиянию кривизны земли на высоты
В практике инженерно-геодезических работ высоты точек и превышения между точками, как правило, требуется знать с ошибкой не более 1 мм. Значит, влияние кривизны Земли на превышения и высоты следует учитывать практически всегда. |