реферат на тему элементы математической логики. Методическое пособие для проведения кружка по геометрии, разработать эор по теме Элементы математической логики
 Скачать 231.69 Kb. Скачать 231.69 Kb.
|
СодержаниеВведение 3 Глава 1. Теоретическая часть 5 §1. Алгебра высказываний 5 §2. Логичесикие операции 5 §3. Формулы алгебры логики 8 §4. Множество. Операции над множеством 9 5. Законы алгебры множеств. Соответствии между операциями алгебры множеств и алгебры логики 12 §6. Разработка ЭОР. Теоретическая часть 13 Глава 2. Практическая часть 14 §1. Решения задач базового уровня 14 §2. Решения задач профильного уровня 15 §3. Решение задач повышенного уровня 16 §5. Разработка ЭОР. Практическая часть 16 Глава 3. Контрольная часть 17 Заключение 19 Библиотический список 20 ВведениеПроизводственная практика (проектно-технологическая), предусмотрена федеральным государственным образовательным стандартом высшего образования и является обязательным элементом учебного процесса, ориентированного на научно-исследовательскую и профессионально - практическую подготовку обучающихся. Проектно-технологическая практика направлена на подготовку бакалавра к последующей научно-исследовательской деятельности в системе высшего образования или при последующем обучении в магистратуре. Термин «логика» происходит от греческого слова «логос», что означает «слово», «мысль». Основоположником логики как науки является древнегреческий ученый Аристотель (384 – 322 гг. до н.э.). Логика, созданная Аристотелем, носит название «традиционная или формальная логика», она есть наука о законах и формах правильного мышления. На протяжении многих веков логика Аристотеля дополнялась, усовершенствовалась различными философами, целыми философскими школами. Цель данной практики: разработать методическое пособие для проведения кружка по геометрии, разработать ЭОР по теме «Элементы математической логики». Задачи практики: Осуществить поиск информации, опираясь на программу исследования; Проанализировать литературу по заданной теме; Получить новые знания на основе анализа, и других методов в области школьного образования; Разработать методическое пособие из раздела «Элементы математической логики» по геометрии; Разработать вопросы, связанные с данной темой; Разработать электронный образовательный ресурс по теме «Элементы математической логики». Методы исследования: анализ научной и учебной литературы, наблюдение, обобщение опыта обучения математике и информатике. Глава 1. Теоретическая часть§1. Алгебра высказыванийВысказывание и его логические операции Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь». Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... то ...», «тогда и только тогда», принято называть сложными или составными. Сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются малыми буквами латинского алфавита: х, у, z, ..., а, b, с, ...; истинное значение высказывания цифрой 1, а ложное значение - буквой цифрой 0. Если высказывание а истинно, то будем писать а = 1, а если а ложно, то а = 0. §2. Логичесикие операцииОтрицанием высказывания х называется новое высказывание 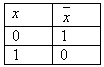 Таблицы такого вида принято называть таблицами истинности. Пусть х высказывание. Так как Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно Конъюнкция высказываний х и у обозначается символом х&у (  Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно. Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний. Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у», читается «х или у». Высказывания х, у называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:  В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях. Импликация высказываний х, у обозначается символом 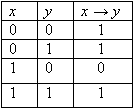 Употребление слов «если.... то...» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х. Употребление слов «если ..., то ...» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается. Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если х, то у». Если при этом известно, что х истинно и доказана истинность импликации Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквивалентность высказываний х, у обозначается символом 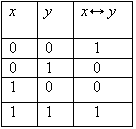 Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности. §3. Формулы алгебры логикиВыражение, составленное из логических переменных с помощью операций над высказываниями и обращающееся в конкретное высказывание при подстановке вместо логических переменных конкретных высказываний, называется формулой высказываний. Таким образом, появляется возможность применять логические операции многократно, получая с их помощью всё более сложные высказывания. При этом возникает одно затруднение: при записи сложных высказываний может оказаться неясным порядок, в котором следует проводить операции. Если формула не содержит скобки, то прослеживается следующий приоритет логических операций: инверсия, конъюнкция, дизъюнкция, импликация (эквиваленция). Логические функции, истинные на всех наборах значений входных переменных, называются тождественно-истинными (тавтологией). Логические функции, ложные на всех наборах значений входных переменных, называются тождественно-ложными. Если у двух логических функций (формул) совпадают таблицы истинности, то есть на всех наборах значений входных переменных они принимают одинаковые значения, то их называют равносильными. Таблица истинности – это табличное представление логической формулы, в котором перечислены все возможные сочетания значений истинности входных сигналов вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значений формулы.  Порядок выполнения логических операций в сложном логическом выражении. Для изменения указанного порядка выполнения операций используются круглые скобки: Инверсия→Конъюнкция→Дизъюнкция→Импликация→Эквивалентность Алгоритм построения таблиц истинности для сложных выражений: 1. Определить количество строк: количество строк = 2n+ строка для заголовка, n – кол-во простых высказываний. 2. Определить количество столбцов: количество столбцов = кол-во переменных + кол-во логических операций o определить количество переменных (простых выражений); o определить количество логических операций и последовательность их выполнения. 3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.  §4. Множество. Операции над множествомМножеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое". Следующие совокупности объектов являются множествами: множество деревьев в лесу, множество целых чисел, множество корней уравнения exsinx = 0.5. Всякое множество состоит из элементов. Множества обозначают большими буквами А, В, С, а элементы – маленькими буквами а, b, c. А = {a1, a2, a3} – множество, состоящее из трех элементов; А = {a1, a2, …} – множество, состоящее из бесконечного числа элементов. Если элемент a принадлежит множеству А - a Î А Если элемент a не принадлежит множеству А- a Ï А. Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А = В. Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В,и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А. Если А Í В и В Í А, то по ранее введенному определению А = В. Пусть А – множество четных чисел, В – множество целых чисел, С –множество нечетных чисел. Тогда А Ì В, С Ì В, А Ë С, В Ë А. Множество, не содержащее ни одного элемента, называется пустыммножеством и обозначается Æ. Существуют следующие способы задания множеств: 1. Перечислением элементов множества. A = {1, 3, 5, 7, 9} – конечное множество; B = {1, 2, …, n, …} – бесконечное множество. 2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: A = {açуказание свойства элементов}. Здесь a является элементом множества A, a Î А. A = {a ça – простое число} – множество простых чисел; B = {b çb2 – 1 = 0, b – действительное число} – множество, состоящее из двух элементов, B = {– 1, 1}; Z = {x ç Операции над множествами Объединением множеств А и В называется множество АvВ, все элементы которого являются элементами хотя бы одного из множеств А или В: а) Пусть А = {4, 5, 6}, В = {2, 4, 6}.Тогда А vВ = {2, 4, 5, 6}. б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда АvВ множество чисел, которые делятся на 2 или на 3: АvВ = {2, 3, 4, 6, 8, 9, 10, …}. Пересечением множеств А и В называется множество А В, все элементы которого являются элементами обоих множеств А и В: а) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда АВ = {4, 6}. б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А В множество чисел, которые делятся и на 2 и на 3: А В = {6, 12, 18, …}. Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество. Относительным дополнением множества В до множества А называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В Тогда А \ В – множество чисел, которые делятся на 2, но не делятся на 3, а В \ А – множество чисел, которые делятся на 3, но не делятся на 2: А \ В = {2, 4, 8, 10, 14, …}. В \ А= {3, 9, 15, 21, 27, …}. Универсальным множеством называется такое множество U, что все рассматриваемые в данной задаче множества являются его подмножествами. Абсолютным дополнением множества А называется множество Пусть А – множество положительных четных чисел. Тогда U – множество всех натуральных чисел и Счетные множества Можно сказать также, что множество счетно, если его элементы можно перенумеровать. 1. A1 = {–1, –2, …, – n, …}; 2. A2 = {2, 22, …, 2n,…}; 3. A3 = {2, 4, …, 2n,…}; 4. A4 = {…, – n, …, – 1, 0, 1, …, n,…}; Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел. Существуют бесконечные множества, элементы которых нельзя перенумеровать. Такие множества называются несчетными. 5. Законы алгебры множеств. Соответствии между операциями алгебры множеств и алгебры логикиПроведем аналогию с алгеброй логики. Используя определения множественных операций, сопоставим их операциям алгебры логики. Вспомните законы алгебры логики, и «переведите» их на язык алгебры множеств.  Любой из этих законов легко доказывается с помощью известного нам метода – с помощью диаграмм Эйлера-Венна. Мы доказывать все эти законы не будем (это элементарные вещи), оставьте страницу и докажите их самостоятельно. Но чтобы не быть голословными, давайте выберем любой из законов и проверим. С помощью кругов Эйлера можно доказать следующие свойства множеств, справедливые для произвольных множеств А, В, С и D: 1) 2) 3) 4) 5) 6) §6. Разработка ЭОР. Теоретическая частьБыл разработан ЭОР, который включает в себя всю теоретическую часть по теме «Элементы математической логики». Ресурс состоит: «Содержания», «Полезные ссылки» и «Теоретическая часть» Глава 2. Практическая часть§1. Решения задач базового уровняЗадача 1 «Сегодня суббота или воскресенье» Решение. Пусть A — «сегодня суббота», а B — «сегодня воскресенье». Тогда «сегодня суббота или воскресенье» представимо формулой: A ⊕ B .(Это сложное высказывание состоит из двух простых высказываний A и B,соединенных связкой «или» в разделительном смысле.) Задача 2 «В квартире грязно и холодно». Решение. Пусть A — «в квартире грязно», а B — «в квартире холодно». Тогда «в квартире грязно и холодно» представимо логической формулой: A& B Задача 3 «Если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном настроении или с головной болью». Решение. Пусть: A — «допоздна работаешь с компьютером», B — «пьешь много кофе», C — «утром просыпаешься в дурном настроении», E — «утром просыпаешься с головной болью». Тогда сложное высказывание «если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном настроении или с головной болью» представимо формулой: (A&B)→(C˅E) §2. Решения задач профильного уровняЗадача 1 Доказать с помощью равносильных преобразований равносильность формул: A→(B→C)≡A˄B→C Решение. Приведем левую часть к правой: A→(B→C)≡  ˅( ˅( )≡( )≡(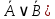 ˅ C≡ ˅ C≡  При выполнении данного задания использовались законы 15-й, закон, выражающий ассоциативность дизъюнкции, закон де Моргана. Задача 2 Выяснить, является ли следующая формула выполнимой:F=(¬A∨B)→(A∧C) Решение. Построим таблицу истинности заданной формулы, используя определения логических операций. Имеем:  Поскольку на трех наборах (достаточно хотя бы на одном) функция принимает значение 1, то формула выполнима. §3. Решение задач повышенного уровняЗадача 1 Задача 1. Построить всевозможные высказывания из двухместного предиката x=y=7, заданного на множестве целых чисел Z Решение. (  y)(x=y=7) – предикат одноместный; ( y)(x=y=7) – предикат одноместный; ( )( )( )(x+y=7) – истинное высказывание; ( )(x+y=7) – истинное высказывание; ( x)( x)( y)(x+y=7) – ложное высказывание. y)(x+y=7) – ложное высказывание.§5. Разработка ЭОР. Практическая частьПрактическая часть содержит разборы решения задач разных уровней сложности (рис. 2). Глава 3. Контрольная часть1. Укажите, какое из следующих предложений является высказыванием: 1) Доброе утро! 2)  ; ; 3) Сколько у вас детей? 4) 14 делится на 7. 2. Установите, какое из следующих высказываний является истинным: 1)  ; 2) 18 делится на 5; ; 2) 18 делится на 5; 3) Лондон – столица Франции ; 4)  . .3. Укажите название закона логики высказываний  : :1) закон двойного отрицания; 2) закон исключенного третьего; 3) закон идемпотентности; 4) закон контрапозиции. 4. С помощью равносильных преобразований упростите формулу:  . .1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . .5. Формулу  преобразуйте так, чтобы она содержала только операции отрицание и конъюнкция: преобразуйте так, чтобы она содержала только операции отрицание и конъюнкция:1)  ; 2) ; 2)  ; ; 3)  ; 4) ; 4)  . .6. Найдите дизъюнктивную нормальную форму формулы 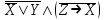 : :1)  ; 2) ; 2)  ; ;3) 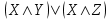 ; 4) ; 4) 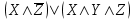 . . 7. Найдите совершенную конъюнктивную нормальную форму формулы  : :1)  ; 2) ; 2)  ; ;3)  ; 4) ; 4)   . .8. Укажите, какая из следующих функций не является булевой функцией: 1)  ; 2) ; 2)  ; ;3)  ; 4) ; 4)  . .9. Укажите, какое из следующих предложений является предикатом: 1)  ; 2) ; 2) 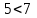 ; 3) ; 3)  ; 4) ; 4) 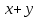 . .10. Определитe множество истинности предиката  , заданного на множестве , заданного на множестве 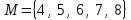 : :1) 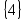 ; 2) ; 2)  ; 3) ; 3)  ; 4) . ; 4) .11. Найдите множество истинности предиката  , заданного на R: 1) , заданного на R: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . .ЗаключениеВ процессе прохождения учебной практики была проанализирована литература по теме «Элементы математической логики», разобраны задачи разных уровней трудности: задачи базового уровня, задачи профильного уровня и задачи повышенной сложности. Каждая задача имеет подробный разбор решение, поэтому переход от одного блока задач к другому не составит труда у обучающихся. Также проверить усвоения знаний поможет раздел «Контрольная часть», который содержит 11 задач на разные уровни сложности. Разработанный электронный образовательный ресурс содержит всю теоретическую и практическую части, контрольная часть состоит из тестирующей программы. Библиотический списокАнисимов А. Е. Сборник заданий по основам программирования./ А.Е.Анисимов, В.В.Пупышев. – М: Интернет-университет информационных технологий, Бином. Лаборатория знаний, 2006. – 352 с. Голубенко Н.Б. Информационные технологии в библиотечном деле. Н.Б .Голубенко. – Ростов-на-Дону: Феникс, 2012. – 288с. Кадыров И. Взаимосвязь внеклассных и факультативных занятий по математике / И. Кадыров. Москва: Просвещение, 1983. 63 с. Решу ЕГЭ / URL: https://ege.sdamgia.ru/ Дата обращения: 07.04.2022. 5. Гурова Л. М., Зайцева Е. В. Математическая логика и теория алгоритмов : учеб. пособие / М. : Изд-во МГГУ, 2006 . – 262 с. 6. Лавров И. А. Математическая логика : учеб. пособие / под ред. Л.Л. Максимовой – М. : Академия, 2006 . – 240 с. 7. Тонких Г.Д. Элементы математической логики: учебно-методическое пособие / Забайкал. гос. ун-т. – Чита, 2016. 119 с. |
