эссе. Эссе. Молекулярнокинетическая теория газов
 Скачать 5.94 Mb.
|
|
"Молекулярно-кинетическая теория газов" молекулярный физика кинетический газ Введение В механике рассматривалось движение материальных точек или твердых тел, форма которых была неизменной, жестко фиксированной. Процессами, которые происходят внутри твердых тел, мы не интересовались. Изучением внутренних свойств вещества занимается молекулярная физика. Молекулярной физикой называется раздел физики, в котором изучаются свойства вещества на основе молекулярно-кинетических представлений. Здесь считается, что вещество состоит из молекул и рассматриваются различные формы движения этих молекул (перемещения, повороты, столкновения, колебания и др.). При изучении вещества приходится иметь дело с системами, содержащими огромное число элементов. В 1 см3 воздуха при нормальных условиях содержится примерно  молекул. Описать движение всех молекул невозможно и не нужно. Для изучения систем, состоящих из большого числа частиц, созданы специальные разделы физики: статистическая физика и термодинамика.Статистической физикой называется раздел физики, в котором свойства вещества и поля исследуются статистическими методами. К статистическим методам можно отнести теорию вероятностей, математическую статистику, теорию случайных процессов и ряд других разделов математики. Молекулярная физика является одним из элементов статистической физики. Термодинамикой называется раздел физики, в котором изучаются общие свойства макроскопических систем с позиций термодинамических законов. Сами термодинамические законы являются обобщением опытных данных. В термодинамике не учитывается молекулярная структура вещества, и ее выводы справедливы для всех макроскопических систем. Молекулярная физика и термодинамика взаимно дополняют друг друга, образуя единое целое, но различаясь методами исследования. Мы будем рассматривать равновесную термодинамику, т.е. изучать общие свойства макроскопических систем, находящихся в состоянии равновесия, а также переходные процессы между состояниями равновесия. Существует также неравновесная термодинамика, позволяющая с позиций общих законов рассматривать неравновесные процессы. 1. Основные понятия статистической физики и термодинамики Термодинамической системой называется совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами. Простейшими примерами термодинамических систем являются газ, жидкость, твердое тело, их соединения и пр. Термодинамическая система характеризуется различными параметрами, важнейшими из которых являются температура Т, давление р, объем V. Их называют параметрами состояния. Состояние системы, при котором параметры состояния не меняются во времени, называют равновесным. Термодинамическим процессом называют переход системы из одного состояния в другое. Такой переход связан с нарушением равновесия системы, когда происходит изменение хотя бы одного из термодинамических параметров. Будем считать, что такое изменение происходит достаточно медленно, так что в любой момент времени состояние системы можно считать почти равновесным (квазиравновесным). Если по координатным осям откладывать значения каких-либо равновесных параметров, то равновесное состояние системы можно изобразить точкой на координатной плоскости. Термодинамический процесс можно изобразить соответствующей термодинамической кривой. На рисунке показана  диаграмма некоторого термодинамического процесса. Система переходит из состояния 1 в состояние 2, оставаясь при этом в состоянии квазиравновесия во всех промежуточных точках. Рис. Процесс называется обратимым, если все его состояния являются равновесными. В противном случае процесс называют необратимым. Круговым процессом или циклом называют процесс, при котором система после ряда изменений возвращается в исходное состояние.  Рис. При молекулярно-кинетическом описании вещества в качестве единицы количества вещества часто выбирают один моль. Молем называют количество вещества, содержащее столько же молекул, сколько атомов содержится в 12 г углерода   . Это число называют числом (постоянной) Авогадро и оно равно  моль-1.Для описания состояния газа обычно используются три параметра: объем, давление и температура. Понятие объема всем известно. Давлением называется физическая величина, численно равная силе, действующей на единицу площади по нормали к ней  .Единицей давления является 1 паскаль  .Часто давление измеряют в атмосферах. Приближенно  .В механике для описания движения материальной точки использовалось понятие координаты, скорости, ускорения, массы, импульса, силы и др. В молекулярной теории от некоторых параметров приходится отказываться (координаты, скорости отдельных частиц и пр.) и вводить ряд новых параметров, которых нет в механике, например, температуру. Температурой называется физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура измеряется в градусах Цельсия ºС или К (существуют и другие системы, напр., шкала Фаренгейта, … ). Если t - температура в градусах Цельсия, а T - температура в градусах Кельвина, то между ними существует отношение  .Отметим, что понятие температуры полностью отсутствует в механике. В статистической физике введение понятия температуры связано с существованием большого числа элементов макроскопической системы (статистический ансамбль) и вводится как некоторая усредненная характеристика энергии отдельной частицы. . Идеальный газ Простейшей моделью, описывающей газы, является модель идеального газа. В этой модели делаются следующие предположения: ) молекулы газа настолько удалены друг от друга, что взаимодействие между ними отсутствует; ) молекулы могут абсолютно упруго сталкиваться друг с другом и со стенками сосуда, в который они помещены; ) собственный объем молекул газа пренебрежимо мал. При не очень больших давлениях большинство газов ведут себя как идеальные. Более сложные процессы, например, превращение газа в жидкость в рамках идеального газа описать нельзя. Для описания состояния газа обычно используются три параметра: объем, давление и температура. Опытным путем, еще до создания молеку4лярно-кинетической теории, был установлен ряд законов, описывающих движение идеальных газов. Рассмотрим эти законы. Закон Авогадро: Моль любого газа при фиксированных значениях давления и температуры имеет один и тот же объем. При нормальных условиях этот объем равен 22,41·10-3 м3/моль. Число молекул в одном моле вещества называют числом Авогадро (постоянная Авогадро): 1/моль.Закон Дальтона: Давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов:  .Отметим, что парциальным давлением газа смеси называется давление, которое оказывал бы один этот газ, если бы он занимал тот же объем при той же температуре. Уравнением состояния газа называется уравнение, устанавливающее связь между параметрами Р, V и Т. Используя полученные из опыта соотношения для идеального газа, Б. Клапейрон получил соответствующее уравнение состояния газа  .Записанное выражение называют уравнением Клапейрона. Входящая сюда величина В изменяется при изменении количества газа. Менделеев записал уравнение Клапейрона для одного моля газа  .Здесь Vm - объем одного моля газа, который, согласно закону Авогадро, является постоянной величиной. Величину R называют молярной газовой постоянной или просто газовой постоянной, ее числовое значение R=8,31 Дж/моль·К. Само уравнение называют уравнением Клапейрона-Менделеева. Молярной массой вещества называется масса одного моля вещества. Если т - масса всего вещества, а μ - масса одного моля, то число молей определяется формулой  .Объем ν молей вещества  и уравнение Клапейрона-Менделеева можно записать в виде .Постоянной Больцмана называется величина  Дж/К.Запишем уравнение состояния для одного моля, выражая давление через температуру и концентрацию молекул:  ,где  - концентрация молекул (число молекул в единице объема).3. Молекулярно-кинетическое описание идеального газа Рассмотрим некоторые характеристики идеального газа с точки зрения молекулярно-кинетической теории. Будем считать, что внутри закрытого сосуда объема V содержится N молекул газа при температуре Т. Молекулы находятся в движении, сталкиваются между собой и со стенками сосуда. При столкновениях происходит обмен энергией между молекулами, а также между молекулами и стенками сосуда. Вычислим давление газа на стенку, используя упрощенную модель. Введем следующие допущения: ) все молекулы имеют одну и ту же скорость v; ) молекулы движутся в трех взаимно перпендикулярных направлениях; ) отражения молекул от стенок абсолютно упругие; ) столкновения между молекулами не учитываются. Если молекула массой  движется перпендикулярно к стенке со скоростью v и упруго отражается, то изменение ее импульса .Записывая закон Ньютона в форме  ,можем найти выражение для давления на стенку, создаваемого одной молекулой при отражении  .Число молекул, долетающих до стенки и попадающих на площадку 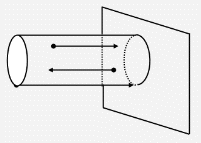 за время  равно числу молекул, содержащихся в цилиндре высотой  и движущихся по направлению к стенке: . Рис. Давление на стенку  .Уравнение  называют основным уравнением молекулярно-кинетической теории идеальных газов. Кинетическая энергия движущейся молекулы определяется формулой  .Следовательно, основное уравнение можно записать по-другому  .Первоначальную упрощенную модель можно сделать более реальной, считая, что молекулы движутся по всем направлениям и могут иметь любую скорость. Средней квадратичной скоростью называется величина  .Учитывая распределение молекул по скоростям и направлениям, основное уравнение молекулярно-кинетической теории газов можно получить в виде  .Сравним полученное выражение с уравнением Клапейрона-Менделеева и введем понятие температуры с молекулярно-кинетической точки зрения. Учитывая, что средняя кинетическая энергия одной молекулы  ,запишем  .Имеем  .Тогда  ,где Е - суммарная кинетическая энергия поступательного движения всех молекул, содержащихся в одном моле. Сравнивая эту формулу с уравнением Клапейрона-Менделеева  ,получим  ,т.е. температура является мерой кинетической энергии молекул. Выразим энергию через температуру:  .Отсюда видно, что средняя кинетическая энергия поступательного движения одной молекулы с точностью до коэффициента  совпадает с температурой Т. В частности, при Т=0 имеем  , т.е. все молекулы неподвижны. Соответственно получим  .Зная температуру Т, легко определить среднюю скорость движения молекул  .При комнатной температуре получим для молекул кислорода О2  м/c, для водорода Н2  м/c.4. Распределение Максвелла Молекулы газа имеют различные направления и скорости. Молекулы взаимодействуют между собой и со стенками сосуда, поэтому в системе устанавливается равновесное распределение молекул по скоростям и направлениям. Рассмотрим такое равновесное распределение. Из соображений симметрии, учитывая отсутствие в пространстве выделенных направлений, ясно, что в равновесном состоянии все молекулы распределены по направлениям равномерно. При каждой температуре существует свое равновесное распределение молекул по скоростям, которое описывается формулой Максвелла. Функцией распределения молекул по скоростям  называется функция, которая определяет относительное число молекул, скорости которых заключены в интервале от v до v+dv: .Можно показать, что функция f(v) определяется выражением:  .Эта функция называется распределением Максвелла. График этой функции показан на рисунке 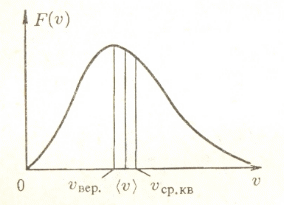 Рис. Из приведенного графика видно, что существует наиболее вероятное значение скорости молекулы. Для его определения надо приравнять нулю производную этой функции. Опуская выкладки, запишем результат  .(получить этот результат самостоятельно). Используя выражения для функции распределения можно получить среднее значение скорости и другие характеристики движения. Найдем выражение для функции распределения молекул по энергиям. Выражая энергию через скорость ,запишем  .Выразим f(v) и dv через ε и dε. После преобразований, учитывая условие  ,получим  .Эта функция описывает распределение молекул по энергиям теплового движения. Среднее значение энергии одной молекулы (математическое ожидание случайной величины ε) определяется формулой  .Для интерпретации этой формулы введем следующее понятие. Числом степеней свободы молекулы называется число независимых переменных, которые полностью определяют положение молекулы в пространстве. Рассмотрим простейшие случаи: одноатомная молекула рассматривается как материальная точка и имеет три пространственные координаты (x,y,z) (три поступательных координаты).  двухатомная молекула может быть представлена в виде  и имеет три поступательных и две вращательных степени свободы. трехатомная и более сложные молекулы имеют три поступательных и три вращательных степени свободы 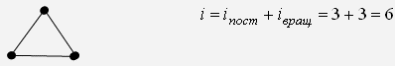 В более сложных случаях следует учитывать наличие колебательных степеней свободы 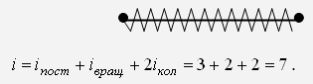 Закон Больцмана о равномерном распределении энергии по степеням свободы: Для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степень свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT. Из закона Больцмана следует, что средняя энергия молекулы определяется формулой  ,где i - число степеней свободы молекулы. Из закона Больцмана вытекает физический смысл температуры: температура - это величина, пропорциональная средней энергии, приходящейся на одну степень свободы. Учитывая наличие различных степеней свободы, можно определить среднюю энергию различных молекул. Энергию одного моля можем записать в виде  ,где R=kNA - термодинамическая постоянная. Для ν молей получим  .Изменение энергии идеального газа при изменении температуры  .При  ,  ,  получим .Отсюда следует физический смысл газовой постоянной: Величина  равна изменению внутренней энергии одного моля идеального газа, приходящемуся на одну степень свободы при изменении температуры на 2К.5. Распределение Больцмана Важную роль в различных приложениях играет формула Больцмана, описывающая изменение плотности газа в различных силовых полях. Рассмотрим сначала изменение атмосферного давления с высотой. Выделим столбик воздуха высотой h и составим уравнение, описывающее изменение давления с высотой. 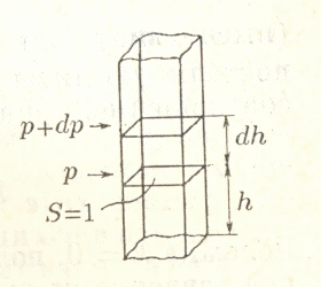 Рис. Имеем  .Полагая  и используя уравнение состояния ,получим  .Следовательно,  , .Учитывая условие  , получим  . Окончательно имеем .Полученную формулу называют барометрической. Она лежит в основе приборов для определения высоты - высотомеров. Запишем уравнение состояния в виде  .Подставляя эти выражения в барометрическую формулу, получим  .Полученная формула называется распределением Больцмана. Она описывает зависимость концентрации молекул воздуха от высоты. График этой функции приведен ниже.  Рис. Выражая молярную массу через массу одной молекулы  ,преобразуем формулу Больцмана к другому виду:  ,где  - потенциальная энергия молекулы в поле тяготения. Отметим, что природа поля U может быть любая. Обычно под распределением Больцмана понимают последнюю формулу.6. Явления переноса Физической кинетикой называется наука, изучающая процессы, возникающие при нарушениях равновесия. При изучении физической кинетики широко используются методы термодинамики, статистической физики и молекулярно-кинетической теории. Из многочисленных проявлений физической кинетики рассмотрим теплопроводность, диффузию и внутреннее трение. При нарушении равновесия система стремится вернуться в равновесное состояние. При этом в системе происходят процессы, связанные с переносом какой-либо физической величины: массы, заряда, энергии, импульса и пр. Отметим, что явления переноса обычно представляют собой необратимые процессы. Потоком физической величины называется количество этой величины, переносимое в единицу времени через заданную поверхность. Примеры: поток жидкости, поток света, поток тепла,… Для простоты будем рассматривать поток через плоскость перпендикулярную оси х. . Теплопроводность. Известно, что тепло передается от более нагретых участков к менее нагретым. Количественно процесс теплопроводности описывается законом Фурье: тепловой поток через площадку S пропорционален градиенту температуры  ,где  - коэффициент теплопроводности. Это эмпирическое уравнение, полученное Фурье. Минус указывает на то, что тепло передается от более нагретых частей к менее нагретым. Используя аппарат молекулярно-кинетической теории, можно показать, что для идеальных газов коэффициент λ определяется формулой ,где  - удельная теплоемкость при постоянном объеме,  - средняя скорость теплового движения молекул,  - средняя длина свободного пробега молекулы.Удельной теплоемкостью при постоянном объеме называется количество теплоты, необходимое для нагревания 1 кг газа на 1ºК при постоянном объеме. Средней длиной свободного пробега молекулы называется средний путь, который проходит молекула между двумя последовательными столкновениями. При теплопроводности происходит перенос энергии от более нагретых областей к менее нагретым. . Диффузия. Диффузией называется самопроизвольное выравнивание концентраций в смеси нескольких различных веществ, вызванное тепловым движением молекул. Если в сосуде, разделенном перегородкой, содержатся различные газы, то после удаления перегородки газы перемешаются. 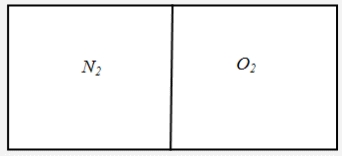 Рис. Диффузия описывается законом Фика: поток массы пропорционален градиенту плотности вещества  ,где D - коэффициент диффузии. Минус указывает на то, что перенос происходит от областей с большей к областям с меньшей концентрацией. Можно показать, что D определяется формулой  .Отметим, что при диффузии происходит перенос массы. . Внутреннее трение (вязкость). Рассмотрим две параллельные плоскости, между которыми находится газ или жидкость. Пусть одна плоскость неподвижна, а вторая движется со скоростью V.  Рис. Между соседними слоями жидкости возникнут силы внутреннего трения, которые описываются законом Ньютона: сила внутреннего трения между двумя слоями газа пропорциональна градиенту скорости  ,где η - коэффициент вязкости. При внутреннем трении возникает поток импульса между слоями жидкости или газа, т.е. здесь передается импульс. Можно показать, что коэффициент вязкости определяется формулой  .Нетрудно проверить, что коэффициенты переноса связаны соотношениями  .Связь между коэффициентами переноса указывает на то, явления переноса имеют общую природу - тепловое движение молекул. 7. Основные формулы молекулярно-кинетической теории 1. Закон Дальтона  .2. Уравнение Клапейрона-Менделеева  ,  .3. Основное уравнение молекулярно-кинетической теории  .. Закон Больцмана  .. Барометрическая формула 6. Формула Больцмана  7. Закон Фурье 8. Закон Фика . Закон Ньютона .Список использованной литературы 1. Трофимова Т.И. Курс физики, М.: Высшая школа, 1998, 478 с. . Трофимова Т.И. Сборник задач по курсу физики, М.: Высшая школа, 1996, 304с . Волькенштейн В.С. Сборник задач по общему курсу физики, СПб.: «Специальная литература», 1999, 328 с. . Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями, М.: Высшая школа, 1999, 592 с. . Все решения к «Сборнику задач по общему курсу физики» В.С. Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с. . Красильников О.М. Физика. Методическое руководство по обработке результатов наблюдений. М.: МИСиС, 2002, 29 с. . Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с. |