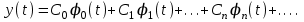Лекция № 1 Обобщенная структурная схема системы передачи информа. Обобщенная структурная схема системы передачи информации
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Л  екция № 1. Обобщенная структурная схема системы передачи информации. Ортогональные и ортонормальные системы функций. Цель: Рассмотреть обобщенную структурную схему системы передачи информации и ортогональные представления сигналов измерительной информации. План: Обобщенная структурная схема системы передачи информации. Виды сигналов измерительной информации. Временная форма представления сигнала. Ортогональные представления сигналов. Ортогональные и ортонормальные системы функций Кусочно-постоянные ортогональные функции: Радемахера, Уолша, Хаара 1. Обобщенная структурная схема системы передачи информации. Обобщенная структурная схема системы передачи информации приведена на рис. 1  Рис.1 Обобщенная структурная схема системы передачи информации. Понятие «информация» является центральным понятием кибернетики. Имеется множество определений понятия «информация»: от наиболее общего философского (информация есть отображение реального мира) до наиболее узкого практического (информация есть сведения, являющиеся объектом хранения, передачи и преобразования). Понятие «информация» есть научное подтверждение гипотезы, что вся материя обладает свойством отражения. Понятие «отражение» как свойство всей материи более общее, чем понятие «информация», являющееся понятием кибернетики и встречающееся только у организованных систем материи, живых организмов и в обществе. Различают понятия «информация» и «сообщение». Сообщение – это форма представления информации. При телеграфной передаче – это текст телеграммы, при разговоре – механические колебания с различной частотой и интенсивностью голосовых связок, при измерении – показания измерительного прибора. Сообщение для передачи его в соответствующий адрес должно быть преобразовано в сигнал. Под сигналом понимается изменяющаяся физическая величина (физический процесс) однозначно отображающая передаваемое сообщение с заданной точностью и пригодная для обработки и передачи на расстояние. Сигнал – это материальный носитель сообщения. Физическая среда, по которой происходит передача сигналов от передатчика к приемнику, называется линией связи. В широком смысле преобразование сообщений в сигнал называется кодированием сообщений. В узком смысле кодирование – это отображение дискретных сообщений сигналами в виде определенных сочетаний символов. Устройство, осуществляющее кодирование называется кодером. С помощью кодирующего устройства сообщение, которое может иметь любую физическую природу, преобразуется в первичный сигнал (для технических устройств обычно в электрический сигнал). Для преобразования первичного сигнала к виду, пригодному для использования в линии связи предназначается передатчик. В передатчике осуществляется воздействие на один или несколько параметров несущей частоты. Этот процесс называется модуляцией, а модулируемые параметры называются информативными. Пример:  При передаче сигналы подвергаются воздействию помех. Под помехами подразумеваются любые мешающие внешние возмущения или воздействия (атмосферные помехи, посторонние источники сигналов), а также искажения сигналов в самой аппаратуре (аппаратурные помехи). На приемной стороне осуществляется обратная операция декодирования, т.е. восстановления по принятому сигналу переданного сообщения. Решающее устройство осуществляет обработку принятого сигнала с целью наиболее полного извлечения из него информации (фильтрация, ограничение, интегрирование, перемножение, сложение и т.д.) Декодирующее устройство (декодер) преобразует принятый сигнал к виду, удобному для восприятия информации. 2. Виды сигналов измерительной информации. Сигнал, как материальный носитель сообщения, представляет собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой величиной х. Такой параметр (у) называется информативным. Существует множество различных видов сигналов. Важным классификационным признаком сигналов является характер их изменения во времени и по информативному параметру (у). Часто изменение сигнала по информативному параметру называют изменением по уровню. Рассмотрим основные виды сигналов, используемых в ИИС. Непрерывные (аналоговые) по уровню и времени.  Рис. 2. Сигналы, непрерывные (аналоговые) по уровню и времени.  , , – измеряемая величина, – измеряемая величина, – информативный параметр. – информативный параметр.Для постоянных токов и напряжений информативными параметрами являются их мгновенные значения. В гармонических сигналах информативными параметрами могут быть амплитуда A, угловая частота  или фаза или фаза  . .Изменение информативного параметра гармонического сигнала в соответствии с изменением измеряемой величины х, называют модуляцией этого сигнала (рис.3). Если с изменением х в гармоническом сигнале меняется один из параметров A,  или или  , то говорят, что осуществляется, соответственно, амплитудная (АМ) (рис.3a), частотная (ЧМ) (рис.3б) или фазовая (ФМ) (рис.3в) модуляции. , то говорят, что осуществляется, соответственно, амплитудная (АМ) (рис.3a), частотная (ЧМ) (рис.3б) или фазовая (ФМ) (рис.3в) модуляции.При фазовой модуляции фаза сигнала определяется относительно второго (опорного) гармонического сигнала у0.
Рис. 3 Виды модуляций сигналов: а) Амплитудная модуляция; б) Частотная модуляция; в) Фазовая модуляция. Непрерывные сигналы по уровню и дискретные по времени. Теоретическая и реальная модель сигналов, непрерывных по уровню и дискретных по времени приведена на рис. 4
Рис. 4. Теоретическая и реальная модели сигнала: а) Измеряемая физическая величина; б) Теоретическая модель амплитудно-импульсной модуляции; в) Реальная модель амплитудно-импульсной модуляции. В реальных системах информативными параметрами могут быть амплитуда, частота или длительность , при этом в зависимости от того, какой из этих параметров функционально связан с х, имеет место соответственно амплитудно-импульсная модуляция (АИМ), частотно-импульсная модуляция (ЧИМ) (рис. 5,а) или широтно-импульсная модуляция (ШИМ) (рис. 5,б) сигнала.
Рис. 5 Виды модуляции; a)Частотно-импульсная модуляция; б)Широтно-импульсная модуляция. 2.3. Сигналы, непрерывные по времени и квантованные по уровню. В таких сигналах информативный параметр может принимать только некоторые разрешенные уровни уi, отстоящие друг от друга на конечные интервалы (кванты) у.  Рис. 6.Сигналы, непрерывные по времени и квантованные по уровню. 2.4. Сигналы, дискретные по времени и квантованные по уровню.  Рис. 7 Сигналы, дискретные по времени и квантованные по уровню. Для описания реальных физических сигналов применяют различные математические модели сигналов: 1. Квазидетерминированные сигналы, т.е. сигналы, у которых известен вид функции, описывающей сигнал, а неизвестными (информативным) являются ее параметры. 2. Случайные сигналы. Сигнал рассматривается как случайный процесс. Описание таких сигналов основывается на теории вероятностей и теории случайных функций. В этом случае изменение сигнала во времени и пространстве характеризуется законом распределения, математического ожиданием, дисперсией и корреляционной функцией. 3. Сигналы представляют в виде комбинации случайной и детерминированной составляющих, в частности в виде суммы сигнала измерительной информации (квазидетерминированная составляющая) и помехи (случайная составляющая). 3.Временная форма представления сигнала. Рассмотрим примеры моделей квазидетерминированных сигналов. При скачкообразном изменении измеряемой величины x(t), сигнал y(t) на выходе безинерционного измерительного преобразователя может быть записан с использованием единичной ступенчатой функции (рис. 8).
Рис.8 Единичная ступенчатая функция С помощью этой функции сигнал измерительной информации может быть записан в виде:  , ,где  – коэффициент преобразования – коэффициент преобразованияСхема получения одиночного прямоугольного импульса приведена на рис. 9
Рис. 9 Схема получения одиночного прямоугольного импульса. Амплитудно - модулированный гармонический сигнал. Амплитудно - модулированный гармонический сигнал приведен на рисунке 10. 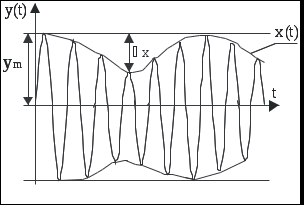 Рис.10 Амплитудная модуляция гармонического сигнала. На рисунке 10 обозначено: 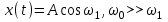 , - изменение физической величины , - изменение физической величины , - изменение модулированного сигнала. , - изменение модулированного сигнала.где  – частота несущих колебаний; – частота несущих колебаний; >> >> m – коэффициент амплитудной модуляции, определяющий влияние x(t) на амплитуду  синусоидальных колебаний; m=x/ синусоидальных колебаний; m=x/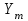 ; ;x – девиация амплитуды. Учитывая, что coscos = ½[cos(+)+cos(-)], получим  Видно, что в сигнале присутствуют колебания трех частот: 0,0-1 и ,0+1 (рис. 11):  Рис. 11 Спектральные составляющие с частотами 0,0-1 и ,0+1 Периодическая последовательность прямоугольных импульсов. Периодическая последовательность прямоугольных импульсов приведена на рисунке 12. Для описания периодической последовательности прямоугольных импульсов постоянного тока применяют выражение:  где Ym – амплитуда импульсов, - длительность импульсов. T = tk+1-tk – период  Рис. 12 Периодическая последовательность импульсов. 4. Амплитудно-импульсно модулированный периодический сигнал. Для его математического описания используют следующее выражение:  5. Представление сигналов с помощью –функции. –функция определяется в соответствии с выражением:
 При этом выполняется следующее соотношение:  В общем случае – функция определяется как:
 С помощью функции можно выразить значение реального сигнала U(t) в конкретный момент времени  . .  -это равенство, называемое стробирующим свойством -функции, справедливо для любого текущего момента времени t. Заменив  на t и приняв в качестве переменной интегрирования на t и приняв в качестве переменной интегрирования  , получим: , получим: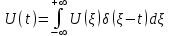 Реакцию системы на произвольный входной сигнал можно определить как суперпозицию реакций на бесконечную последовательность смещенных функций с «площадями», равными соответствующим значениям входного сигнала. Сигналы измерительной информации могут быть описаны на интервале времени t суммой относительно простых функций. В общем случае, для точного описания сигнала, необходимо использовать бесконечный ряд:  где 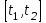 – интервал существования сигнала – интервал существования сигналаВ качестве  нашли применение полиномы Лагранжа, Лагерра, Лежандра, Чебышева и др. нашли применение полиномы Лагранжа, Лагерра, Лежандра, Чебышева и др.При выбранном наборе базисных функции сигнал y(t) полностью определяется совокупностью безразмерных коэффициентов Ск. Такие совокупности чисел называются дискретными спектрами сигналов. Для теоретического анализа базисные функции к(t) нужно выбирать так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость ряда. В случае практической аппроксимации реального сигнала совокупностью базисных сигналов, решающее значение приобретает простота их технической реализации. 4.Ортогональные представления сигналов. Вычисление спектральных составляющих сигнала облегчается при выборе в качестве базиса разложения системы ортогональных функций. Систему функций 0(t), 1(t),к(t), …l(t),…,n(t) называют ортогональной на отрезке 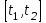 , если для всех k и 1 за исключением случая k = 1, удовлетворяется условие , если для всех k и 1 за исключением случая k = 1, удовлетворяется условие Эта система функций будет ортонормированной (ортонормальной) , если для всех 1  Если это соотношение не выполняется и  то систему можно нормировать, умножая функции l(t) на 1/  Определим коэффициенты Сk при представлении сигнала y(t) совокупностью ортонормированных функций в виде:  , , 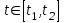 (1) (1)Правую и левую части уравнения (1) умножаем на к(t) и интегрируем на интервале 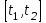 : : В этом уравнении, в силу ортонормированности, остается член суммы с номером k. Тогда имеем:  или, с учетом ортонормированности:  Широко известной ортонормированной системой является совокупность тригонометрических функций:  , ,  , ,  , k=1,2,3 , k=1,2,3Она ортогональна на отрезке [-  , , ]. Так как соответствующее разложение исторически появилось первым, и было названо рядом Фурье, то соотношение (1) называют обобщенным рядом Фурье, а значения Ск - обобщенными коэффициентами Фурье. ]. Так как соответствующее разложение исторически появилось первым, и было названо рядом Фурье, то соотношение (1) называют обобщенным рядом Фурье, а значения Ск - обобщенными коэффициентами Фурье.5. Ортогональные и ортонормальные системы функций Сигналы измерительной информации могут быть разложены по различным ортогональным системам функций 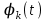 . Систему функций . Систему функций
называют ортогональной на отрезке [t1, t2], если для всех k и l за исключением случая k = l, удовлетворяется условие
При этом предполагается, что  , ,т.е. никакая из функций рассматриваемой системы (2) не равна нулю. Условие (3) выражает попарную ортогональность функций системы (2). Величина 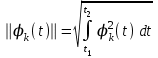 называется нормой функции 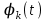 . .Функция 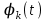 для которой выполняется условие: для которой выполняется условие: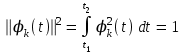 называется нормированной функцией, а система нормированных функций 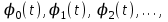 в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой. в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.В математике доказывается, что если функции 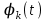 непрерывны, то произвольная кусочно-непрерывная функция y(t), для которой выполняется условие: непрерывны, то произвольная кусочно-непрерывная функция y(t), для которой выполняется условие:
может быть представлена в виде суммы ряда:
В общем случае, для точного описания сигнала, необходимо использовать бесконечный ряд: 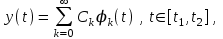 (4) (4)где [t1,t2] – интервал существования сигнала. При выбранном наборе базисных функции сигнал y(t) полностью определяется совокупностью безразмерных коэффициентов Ск. Такие совокупности чисел называются дискретными спектрами сигналов. Для теоретического анализа базисные функции к(t) нужно выбирать так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость ряда. В случае практической аппроксимации реального сигнала совокупностью базисных сигналов, решающее значение приобретает простота их технической реализации. Вычисление спектральных составляющих сигнала облегчается при выборе в качестве базиса разложения системы ортогональных функций. Определим коэффициенты Ск при представлении сигнала y(t) совокупностью ортонормированных функций в виде:  . .Правую и левую части уравнения умножаем на k(t) и интегрируем на интервале [t1, t2]:  . .В этом уравнении, в силу ортогональности, все слагаемые вида  при 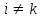 обращаются в нуль. В правой части остается одно слагаемое с номером k. обращаются в нуль. В правой части остается одно слагаемое с номером k. . .Тогда имеем: 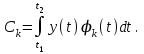 Ортонормированной системой является совокупность тригонометрических функций:  Она ортогональна на отрезке [-, ]. Так как соответствующее разложение исторически появилось первым и было названо рядом Фурье, то ряд (4) называют обобщенным рядом Фурье, а значения Ск – обобщенными коэффициентами Фурье. 5 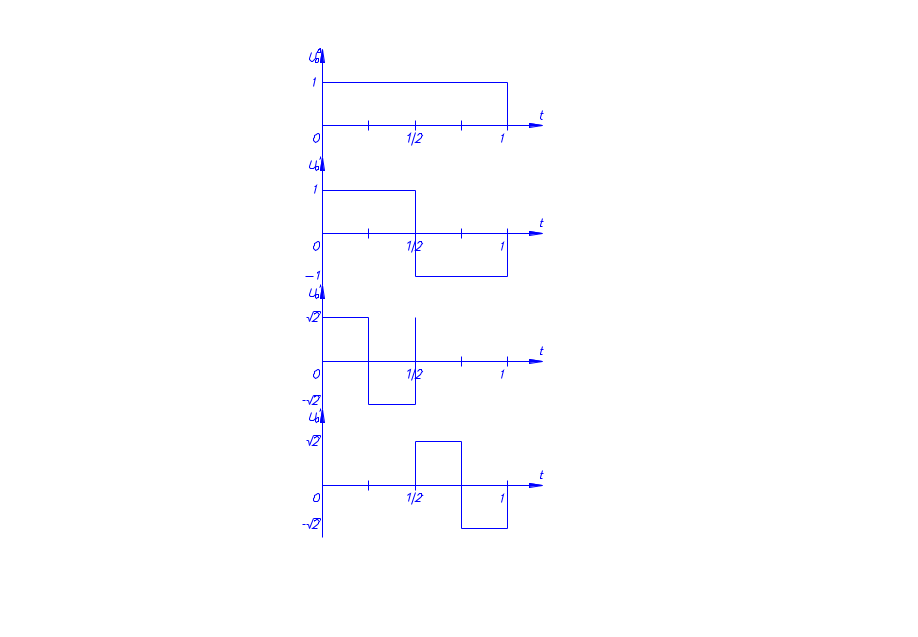 . Кусочно-постоянные ортогональные функции . Кусочно-постоянные ортогональные функцииКроме тригонометрических ортогональных функций могут применяться в качестве базисных и другие ортогональные функции. Особое значение приобретает использование кусочно-постоянных функций, основными среди которых являются функции Радемахера, Уолша и Хаара. Применение преобразования Фурье требует выполнение большого числа умножений на меняющиеся от точки к точке значения косинуса или синуса, которые занимают большую часть машинного времени. Кусочно-постоянная базисная функция имеет на выделенном интервале времени постоянное значение 1, -1 или 0. Поэтому основной причиной применения в качестве базисных кусочно-постоянных базисных функций является существенное упрощение и ускорение обработки информации. Функции Радемахера Функции Радемахера (рис. 13) заданы для значений t в интервале от 0 до Т (Т – период функции). Если использовать относительные единицы  то функции Радемахера задаются в интервале от 0 до 1. Любые две из этих функций взаимно ортогональны. Если за основу принять синусоидальное колебание то функции Радемахера задаются в интервале от 0 до 1. Любые две из этих функций взаимно ортогональны. Если за основу принять синусоидальное колебание  , где m – целое положительное число, и принять для произвольной величины k, что sign k = 1 при k >0 и sign k = -1 при k <0, то функции Радемахера можно представить в следующем виде: , где m – целое положительное число, и принять для произвольной величины k, что sign k = 1 при k >0 и sign k = -1 при k <0, то функции Радемахера можно представить в следующем виде: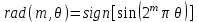 . . Рис. 13. Функции Радемахера. Используется также обозначение  Функции Радемахера являются периодическими 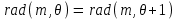 . .В отличие от полного набора синусоид и косинусоид, все функции Радемахера нечетные и, следовательно, не могут быть использованы для аппроксимации четных сигналов. Они образуют неполный набор функций. Поэтому применение их ограничено. Полными ортогональными системами базисных кусочно-постоянных функций являются системы функций Уолша и Хаара. .Ортонормированная система функций УолшаОтрезок существования функций [-Т/2, Т/2], принимаемые значения 1. Если ввести безразмерное время  то k-ую функцию Уолша можно обозначить символом то k-ую функцию Уолша можно обозначить символом  . .На рис. 14 приведены первые 8 функций Уолша. Все функции Уолша ортонормированные, т.е.  и ортогональные. Покажем ортогональность функций Уолша 1-го и 2-го порядков: 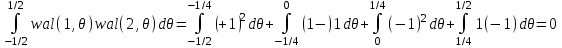 . .Разложение сигнала, заданного на отрезке [-Т/2, Т/2] в обобщенный ряд Фурье по функциям Уолша, имеет вид:   Рис. 14. Первые 8 функций Уолша. Рис. 14. Первые 8 функций Уолша.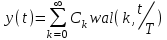 . .Функции Уолша могут быть представлены в виде произведения функций Радемахера  . В таблице 1 приведены 15 функций Уолша, выраженные через функции Радемахера. . В таблице 1 приведены 15 функций Уолша, выраженные через функции Радемахера. Таблица 1.Выражение функций Уолша через функции Радемахера
Номера функций Радемахера, образующих функции Уолша  , определяются по номерам последних, выраженным в двоичном коде Грея. Номера перемножаемых функций Радемахера отвечают номерам разрядов, в которых имеются единицы, закодированного кодом Грея числа n. Разряды отсчитываются, начиная с младшего разряда (справа на лево). Код Грея связан следующим образом с обычным двоичным кодом. Если в обычной двоичной системе счисления число n = ak-1ak-2…a0, то в коде Грея n = bk-1bk-2…b0, где b0 = a0+a1, b1 = a1+a2, …, bk-1 = ak-1; + - знак суммирования по модулю два. , определяются по номерам последних, выраженным в двоичном коде Грея. Номера перемножаемых функций Радемахера отвечают номерам разрядов, в которых имеются единицы, закодированного кодом Грея числа n. Разряды отсчитываются, начиная с младшего разряда (справа на лево). Код Грея связан следующим образом с обычным двоичным кодом. Если в обычной двоичной системе счисления число n = ak-1ak-2…a0, то в коде Грея n = bk-1bk-2…b0, где b0 = a0+a1, b1 = a1+a2, …, bk-1 = ak-1; + - знак суммирования по модулю два.Функции Уолша могут быть заданы и для других интервалов изменения 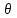 , например, в интервале , например, в интервале  . ..Система функций Хаара (рис. 15). 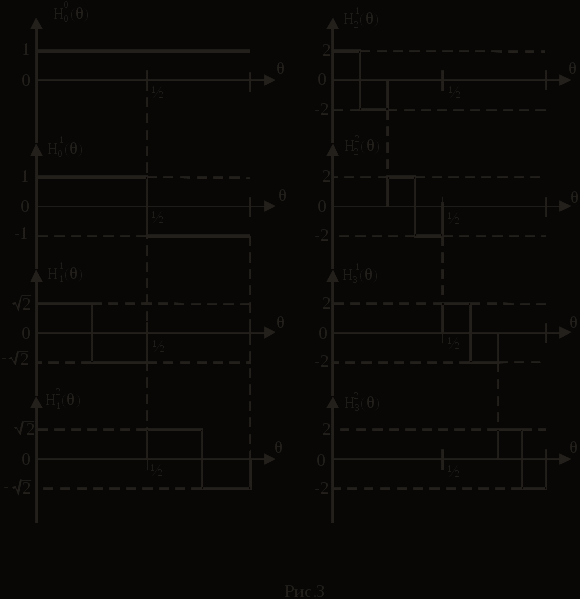  Рис. 15. Функции Хаара. Функция Хаара принимает на разных участках интервала ее задания три различных значения, одно из которых нуль, а два других разные. Контрольные вопросы: 1. Виды сигналов измерительной информации. 2. Временная форма представления сигнала. 3. Ортогональная и ортонормальная система функций. 4. Базисный набор функций. 5. Обобщенный ряд Фурье. 6. Определение коэффициентов 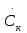 . .7. Кусочно – постоянные ортогональные функции. 8. Функции Радемахера. 9. Функции Уолша. 10. Функции Хаара. 11. Определение функций Уолша через функции Радемахера | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





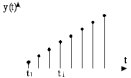






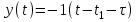
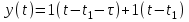


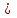
 .
.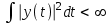 ,
,