|
Общее уравнение плоскости в пространстве имеет вид:
|
1. Ax + By + Cz = 0 2. Ax + By + D = 0
3. Ax + By + Cz + D = 0 4. Ax + By = 0
|
|
Уравнение плоскости, проходящей через точку 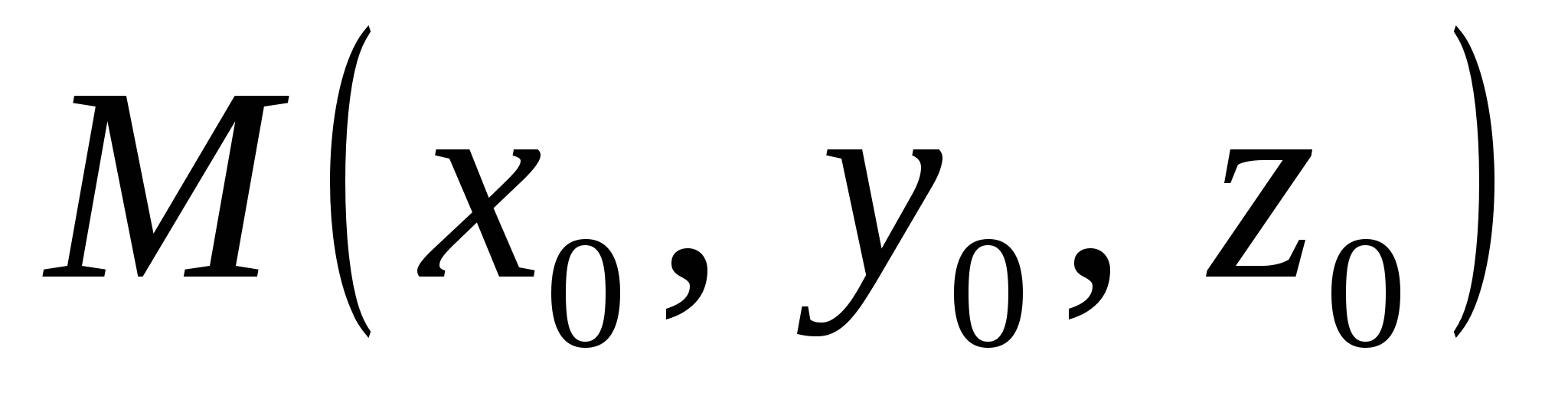 перпендикулярно вектору перпендикулярно вектору 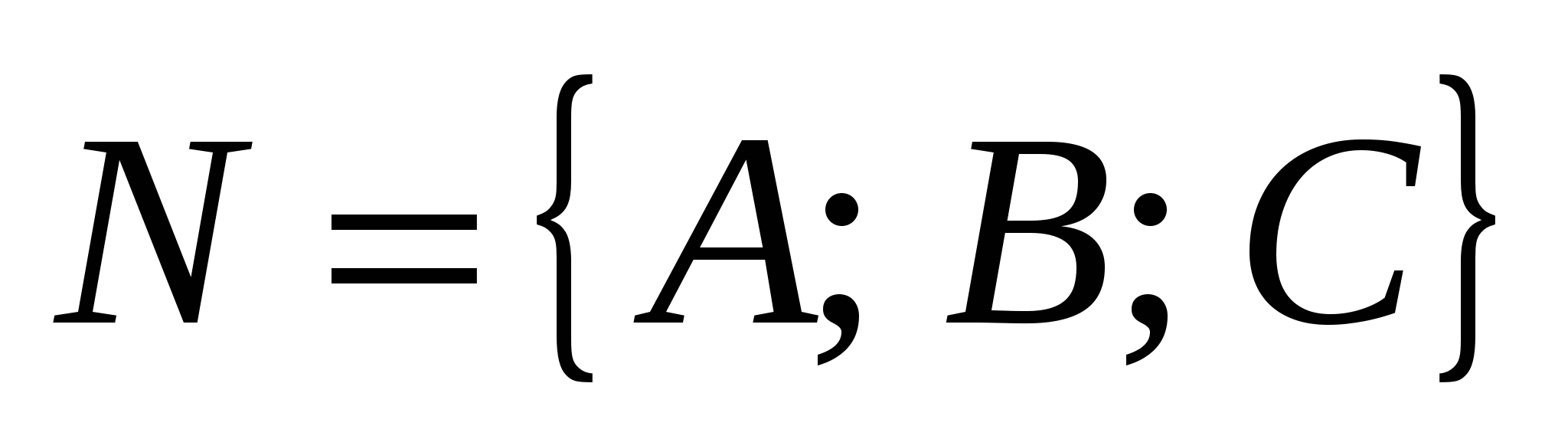 , имеет вид: , имеет вид:
|
1. 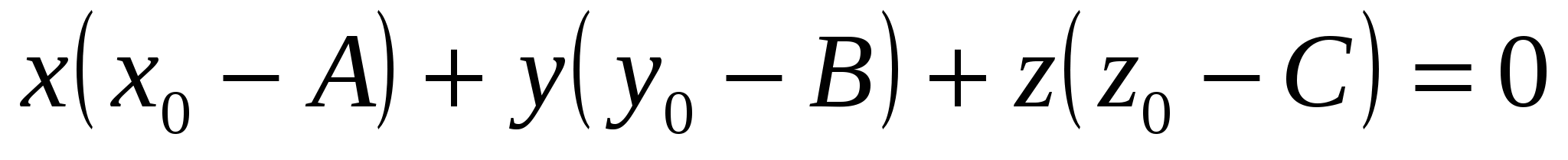
2. 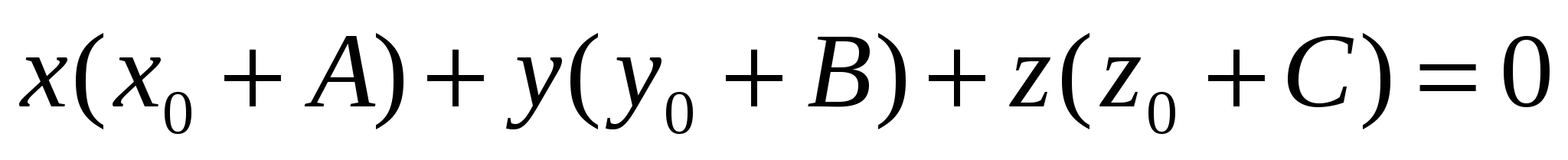
3. 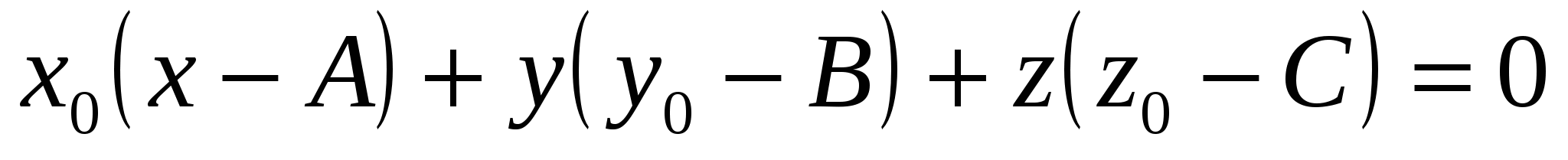
4. 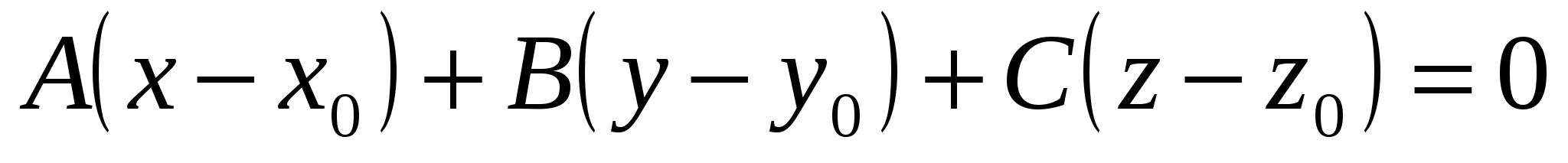
|
|
Какое из уравнений задает плоскость, параллельную оси Ох:
|
1. 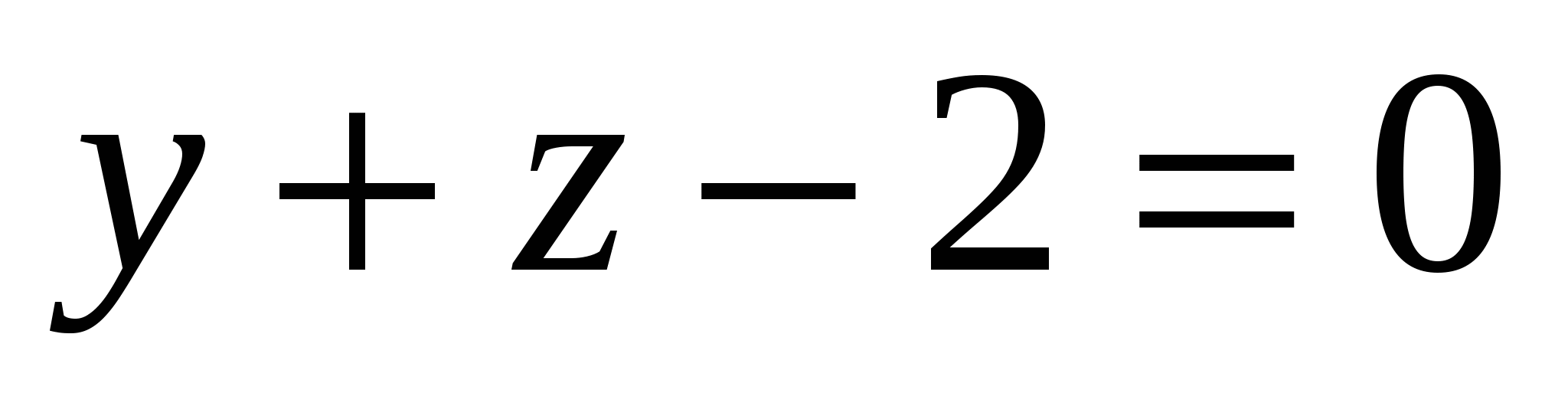 2. 2. 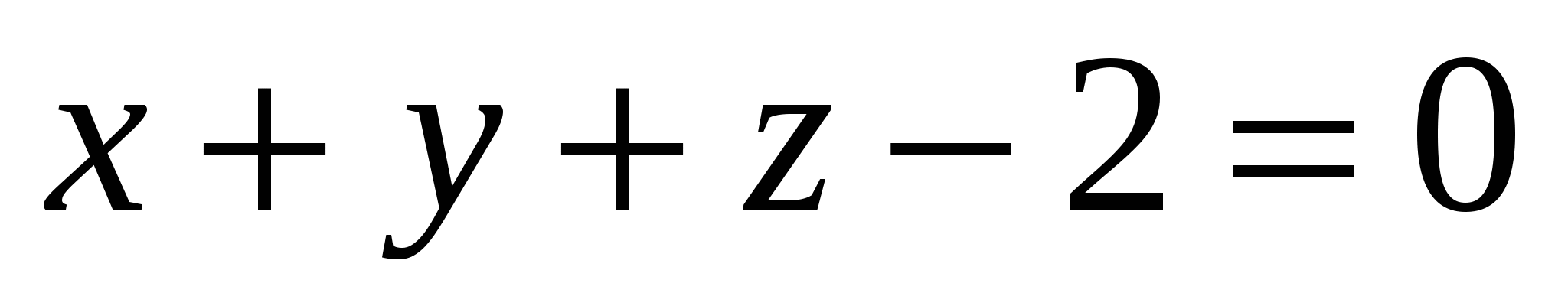
3. 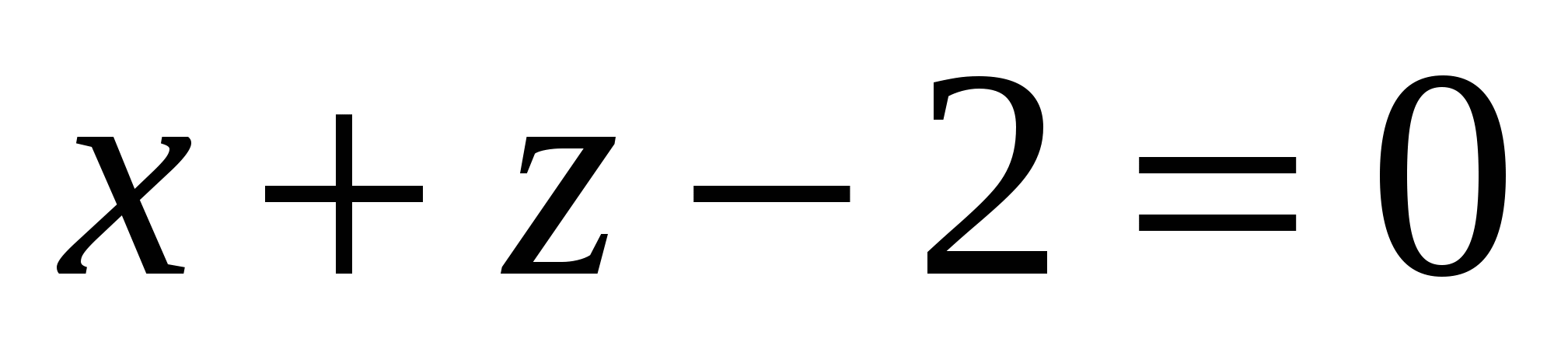 4. 4. 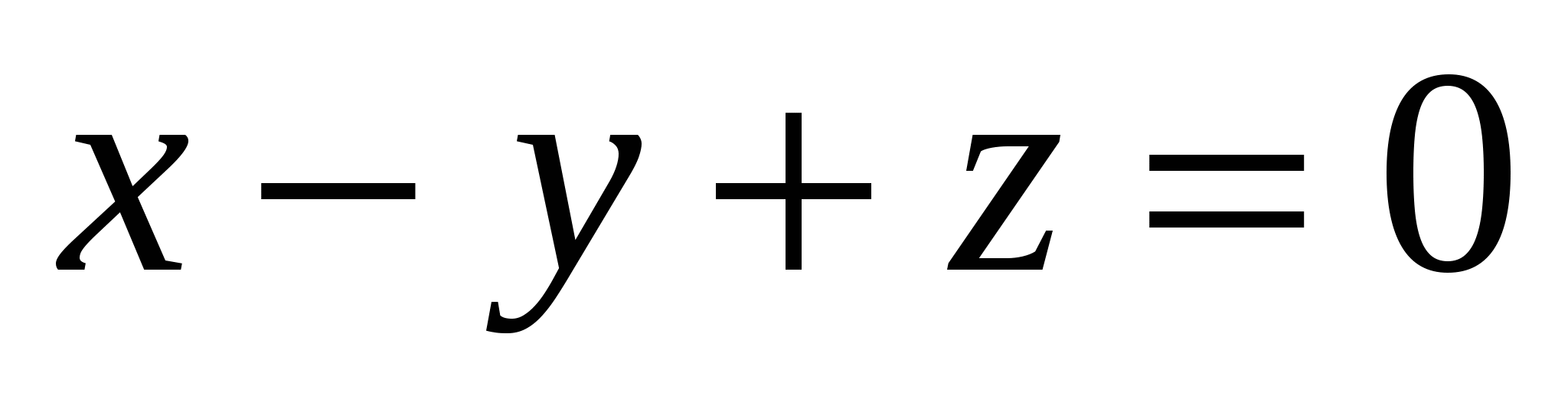
|
|
Какая из заданных плоскостей параллельна плоскости
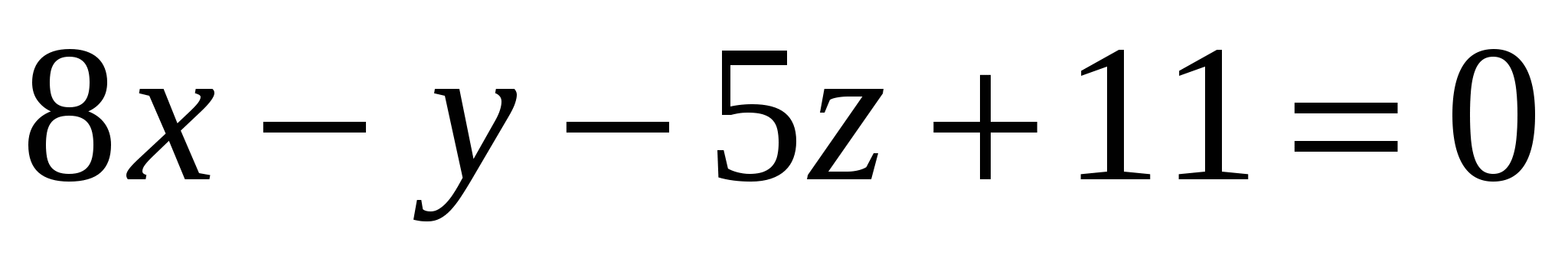 ? ?
|
1. 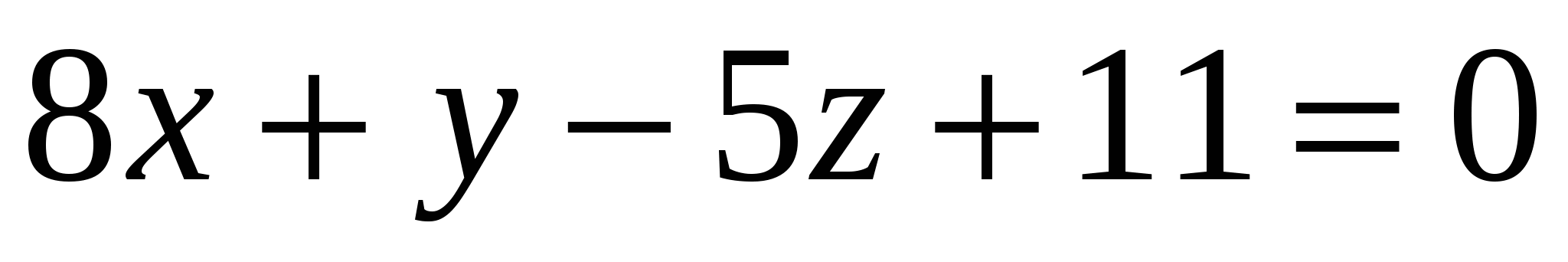
2. 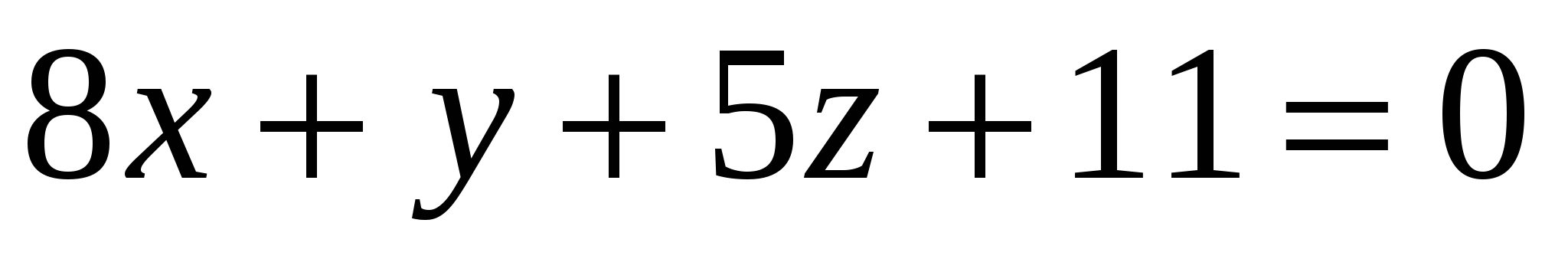
3. 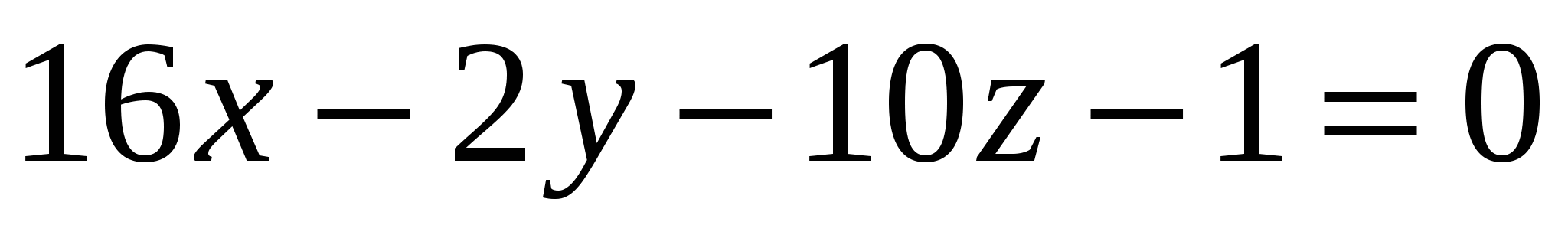
4. Правильного ответа в пп. 13 нет
|
|
Угол  между двумя плоскостями между двумя плоскостями 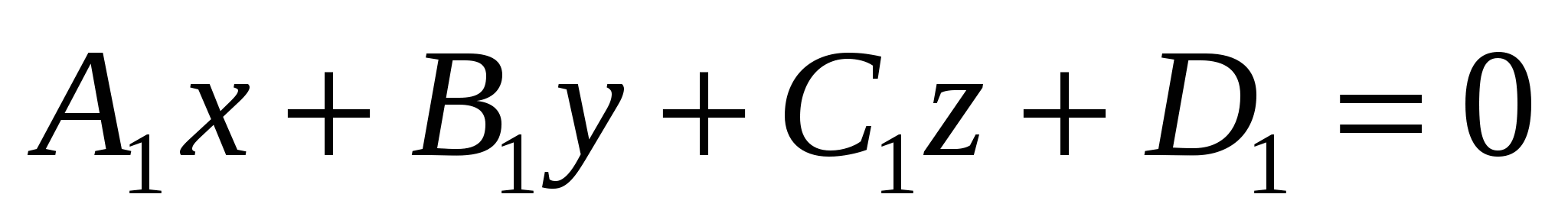 и и 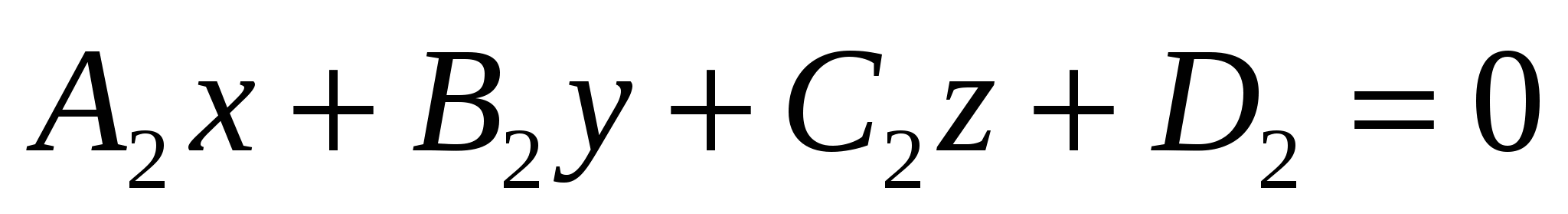 вычисляется по формуле: вычисляется по формуле:
|
1.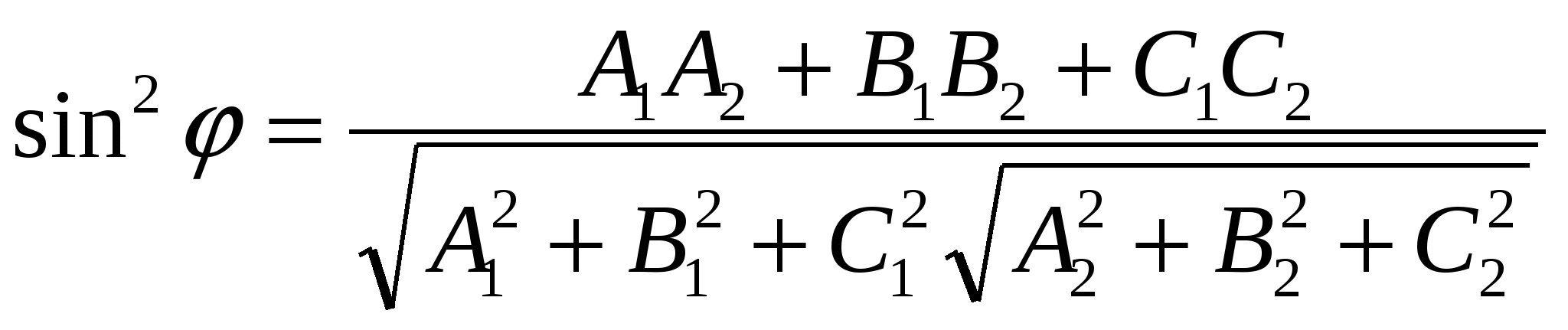 2. 2.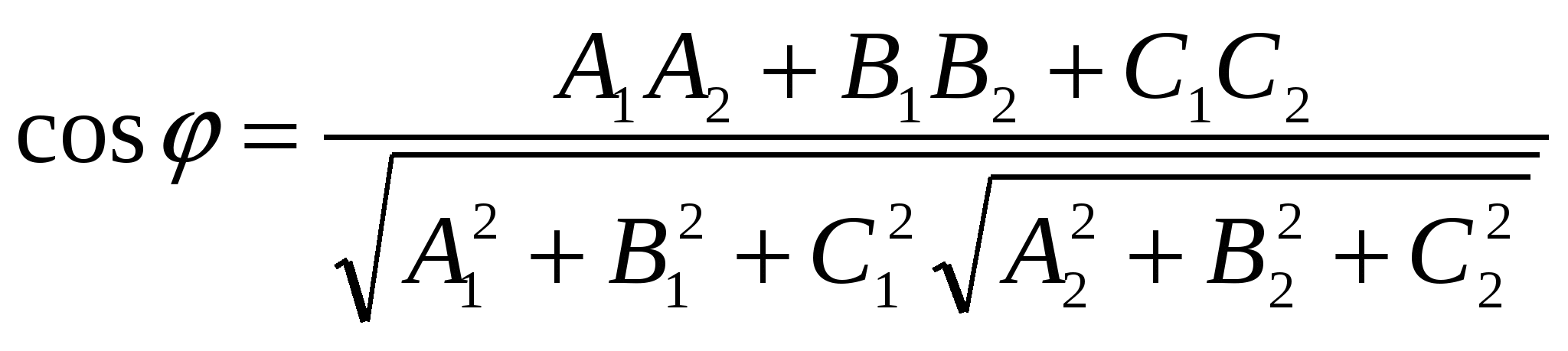
3. 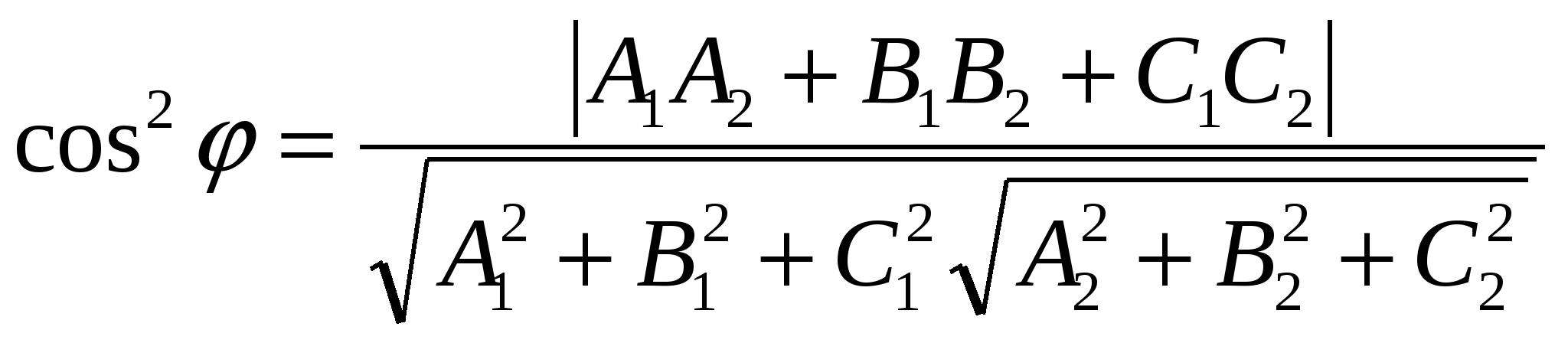
4. правильного ответа в пп. 13 нет
|
|
Какая из заданных плоскостей перпендикулярна плоскости
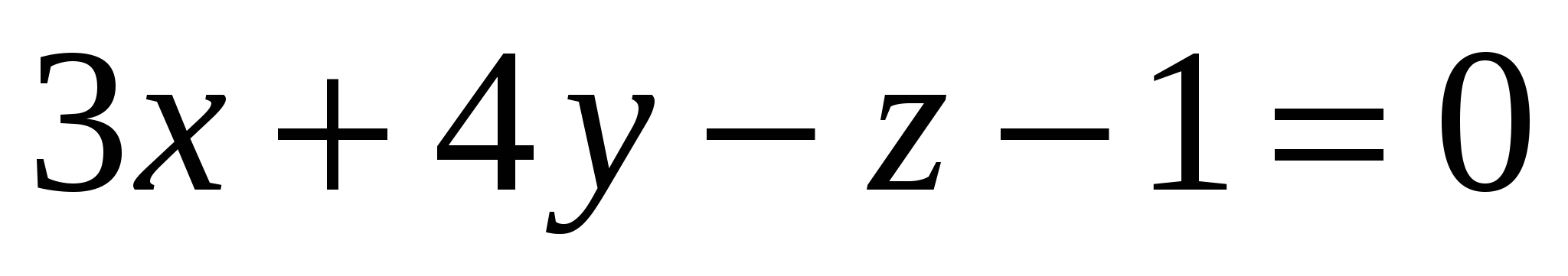 ? ?
|
1. 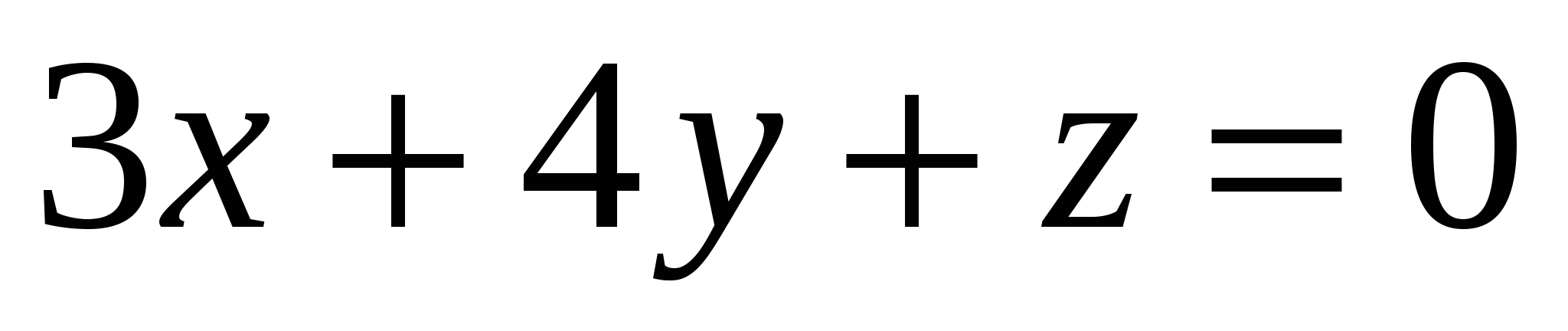 2. 2. 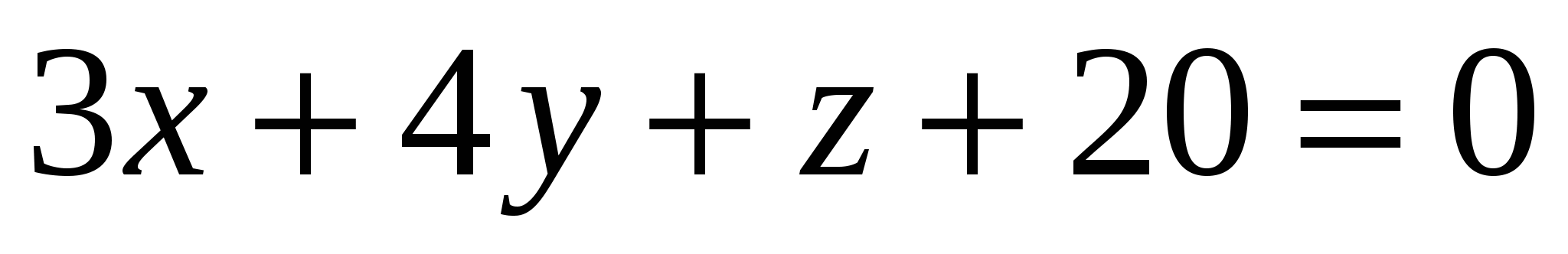
3. 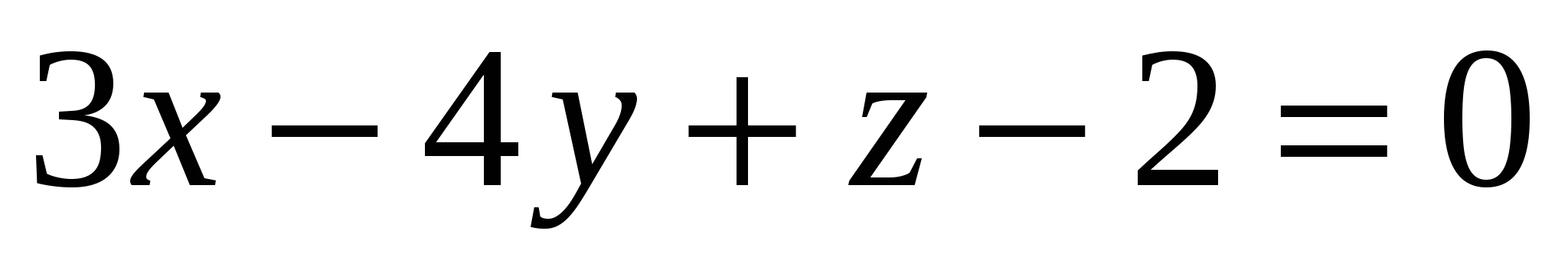 4. 4. 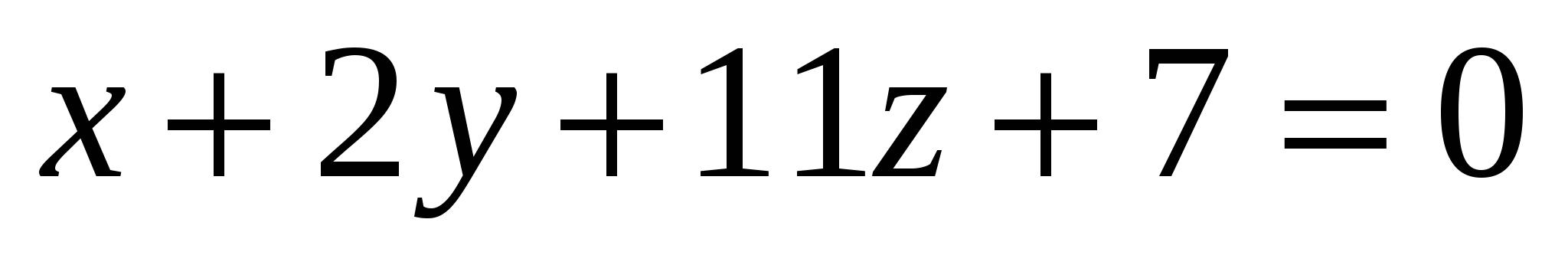
|
|
Если в общем уравнении плоскости
Ax + By + Cz + D = 0
коэффициент D = 0, то эта плоскость …
|
1. Параллельна плоскости Оxу
2. Проходит через начало координат
3. Параллельна прямой x = y = z
4. Правильного ответа в пп. 13 нет
|
|
Заданы уравнения прямой в пространстве 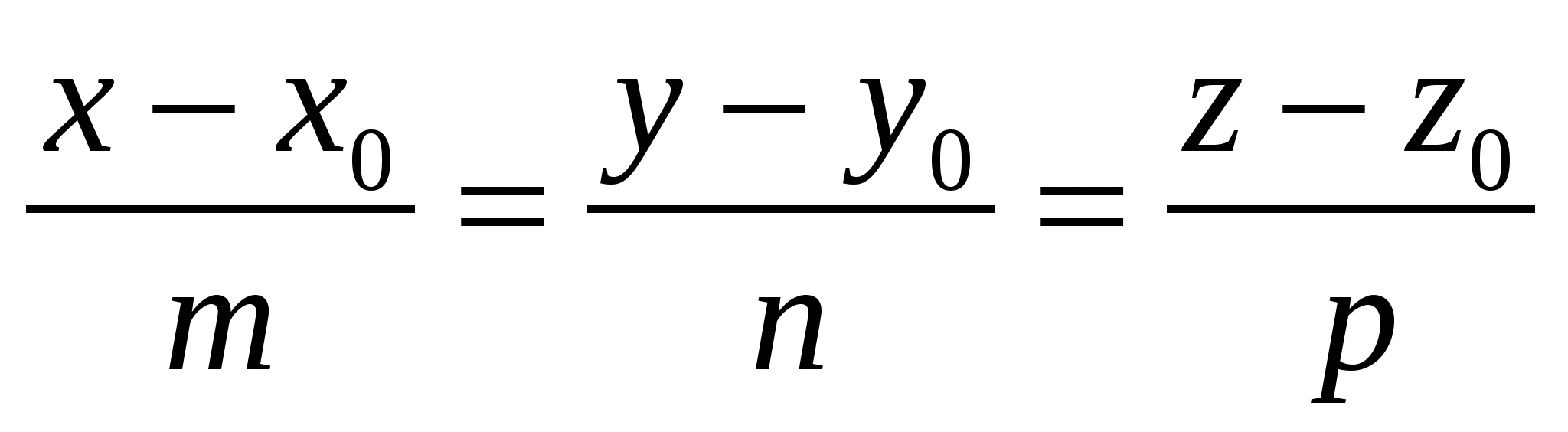 , тогда эта прямая , тогда эта прямая
|
1. параллельна вектору 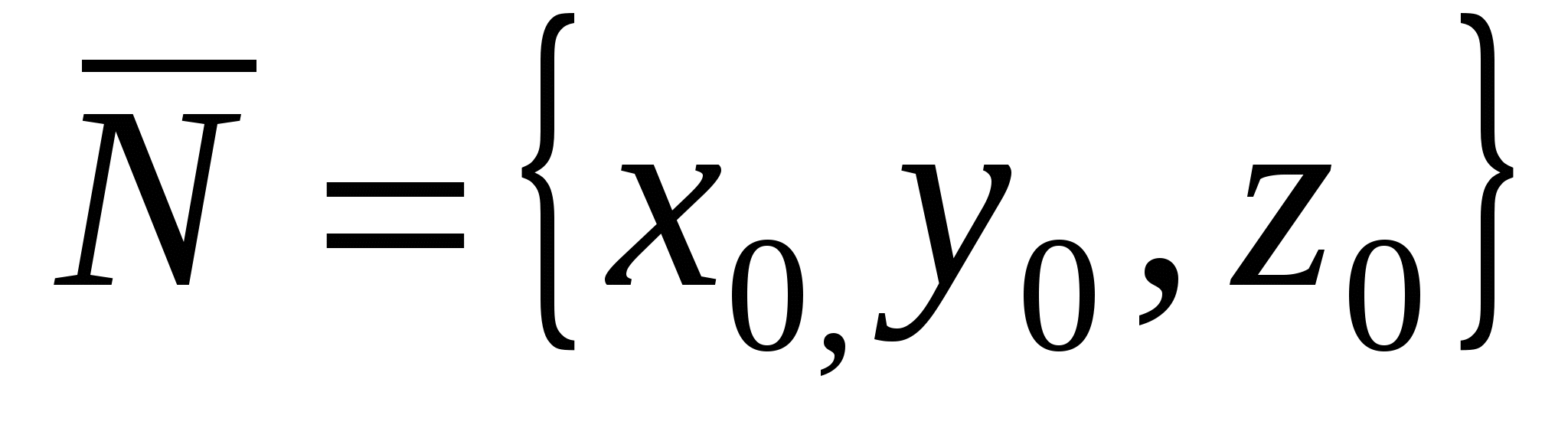
2. перпендикулярна вектору 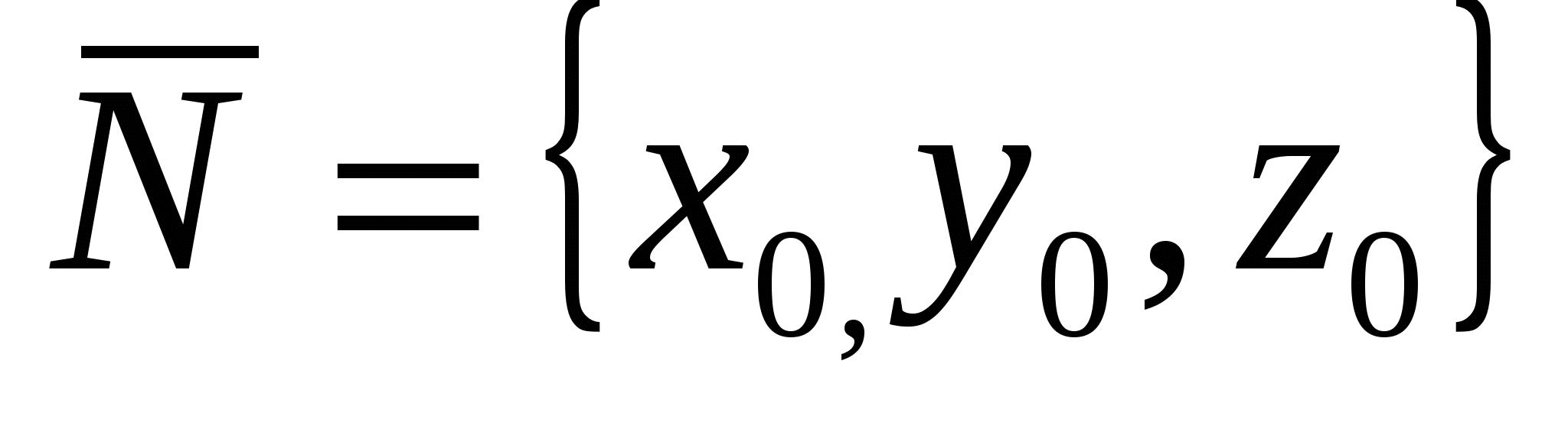
3. параллельна вектору 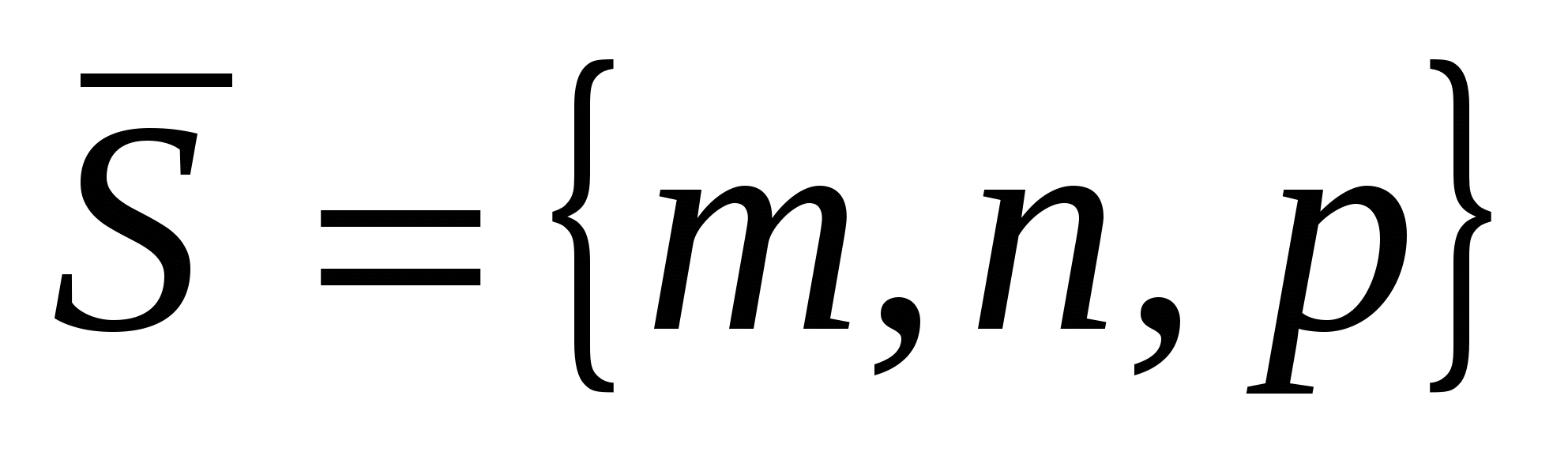
4. перпендикулярна вектору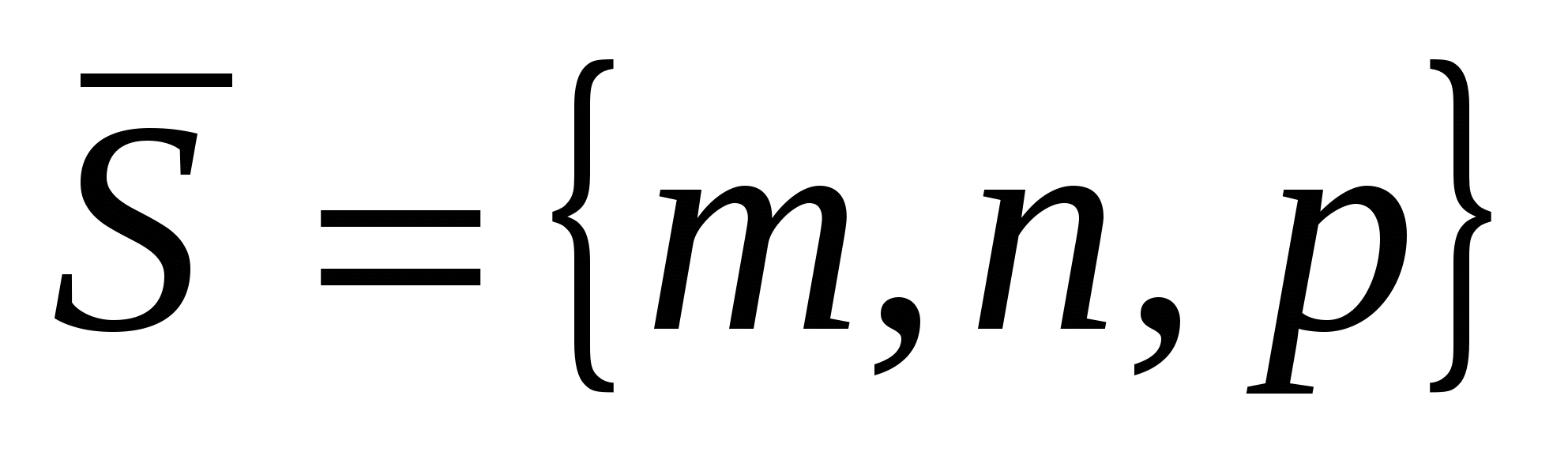
|
|
Укажите, какая из следующих плоскостей перпендикулярна вектору
 = {1; 3; 5} : = {1; 3; 5} :
|
1. 2x + 6y 10 z 11 = 0
2. 2x 6y + 10 z 11 = 0
3. x + y z 110 = 0
4. 5x + y 3 z 16 = 0
|
|
Указать условие параллельности двух плоскостей:
A1 x + B1 y + C1 z + D1=0
и
A2 x + B2 y + C2 z + D2 = 0:
|
1. A1 A2 + B1 B2 + C1 C2 + D1D2 = 0
2. A1 A2 + B1 B2 + C1 C2 = 0
3. 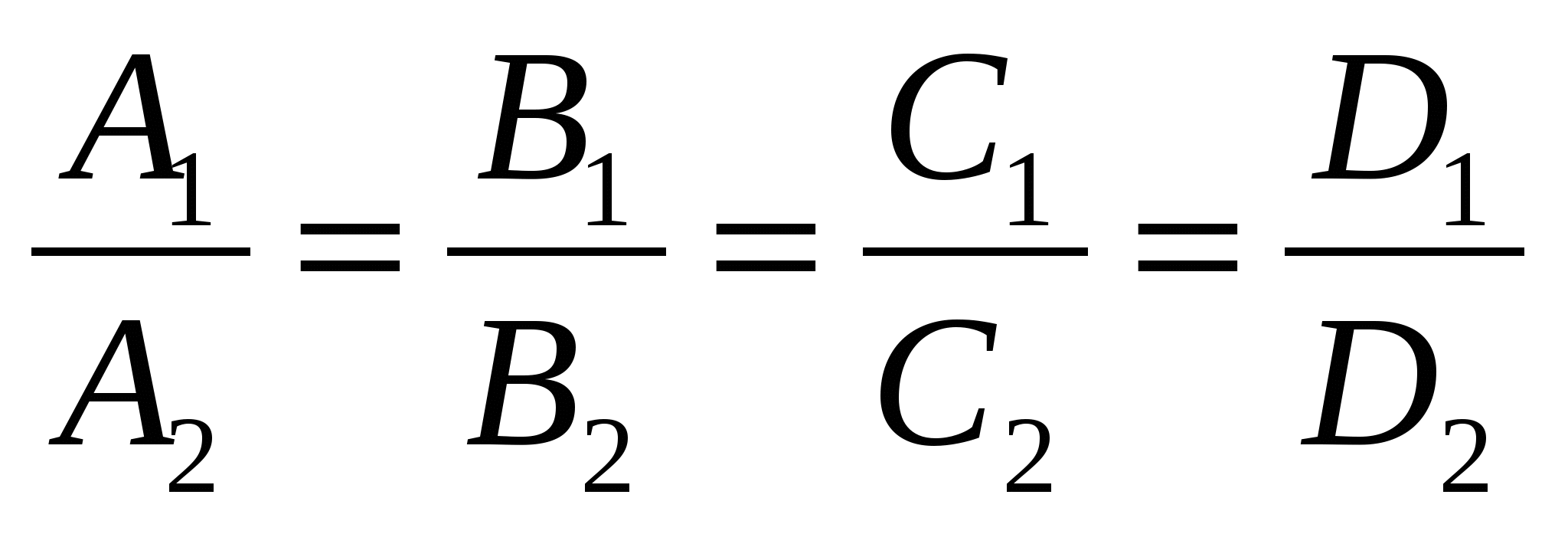
4. 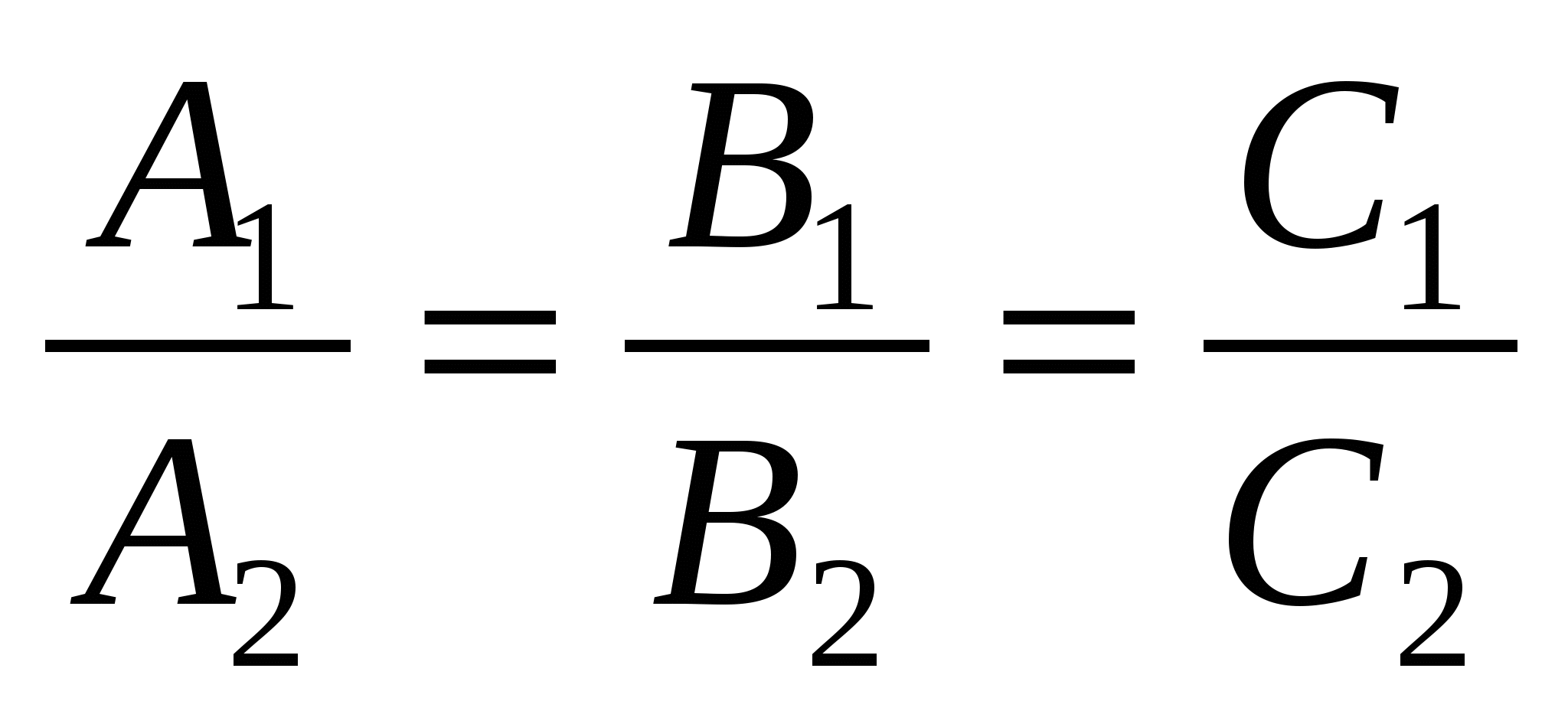
|
|
Расстояние 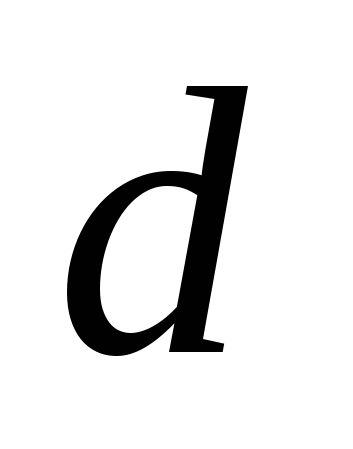 от точки от точки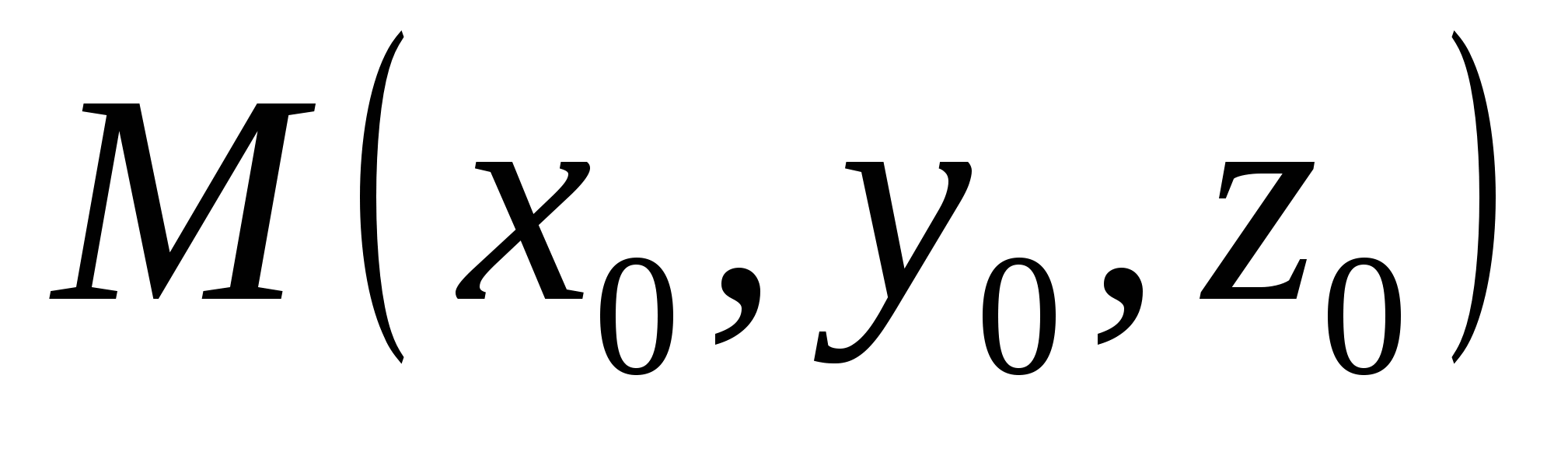 до плоскости до плоскости 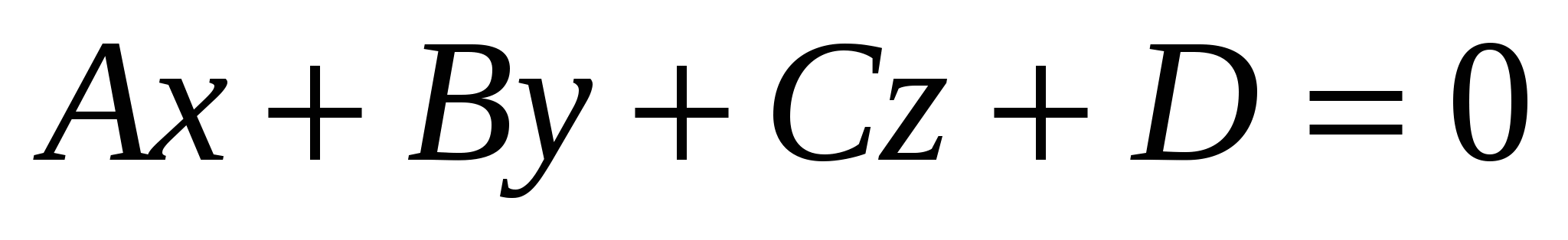 вычисляется по формуле вычисляется по формуле
|
1. 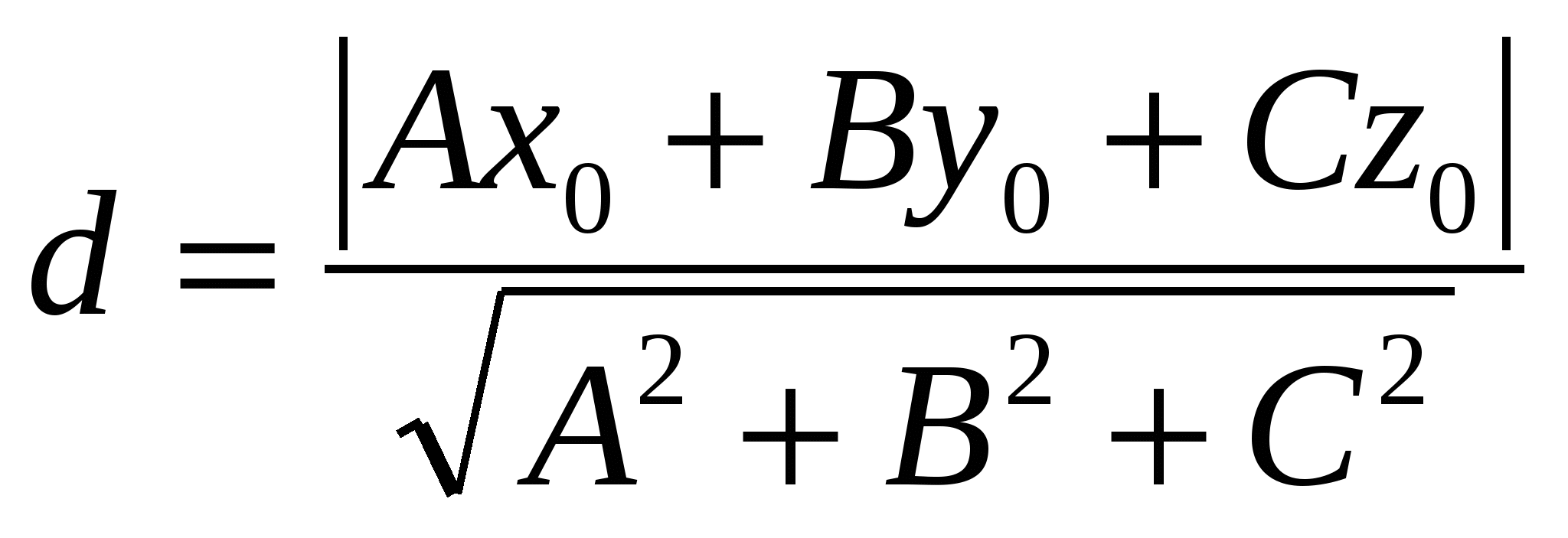
2. 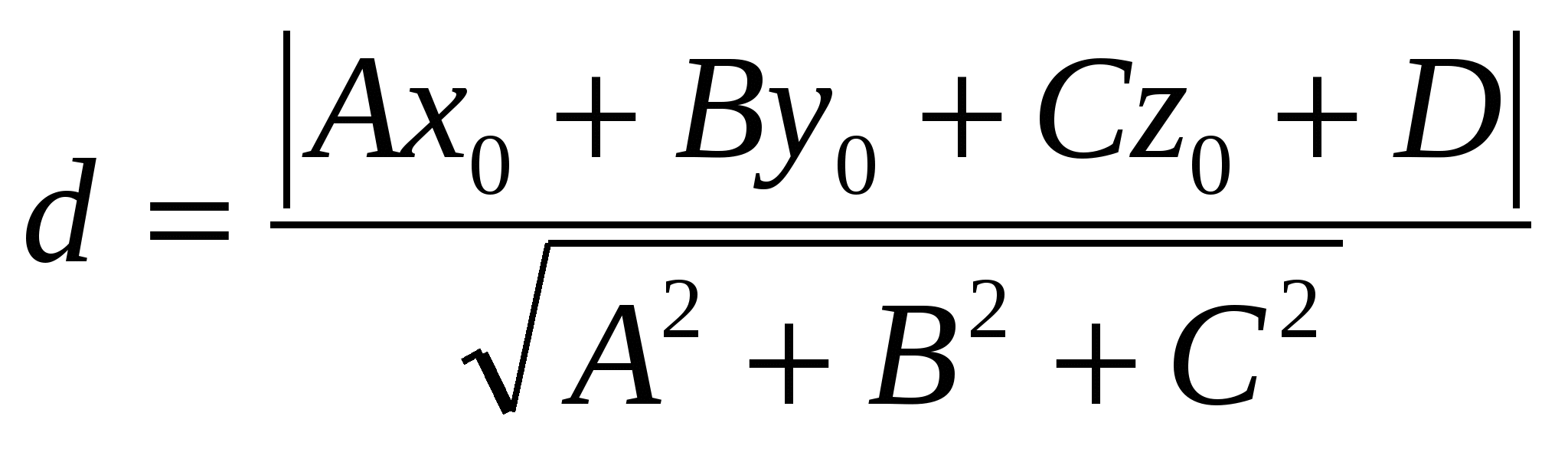
3. 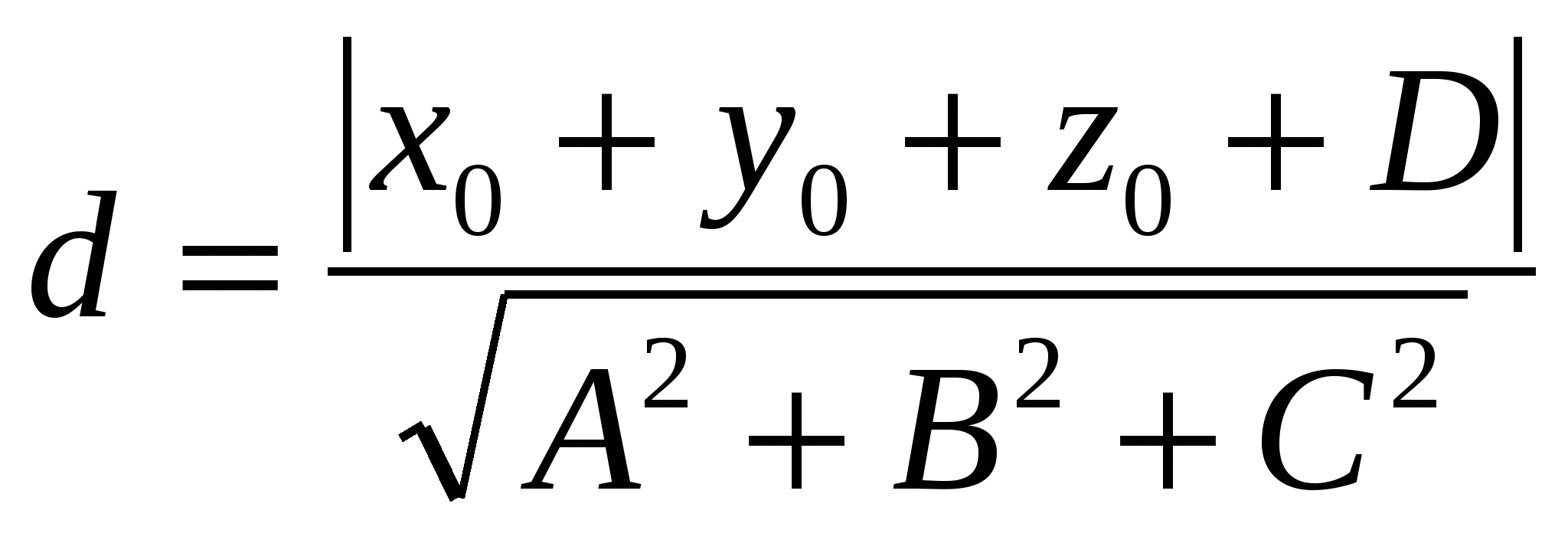
4. 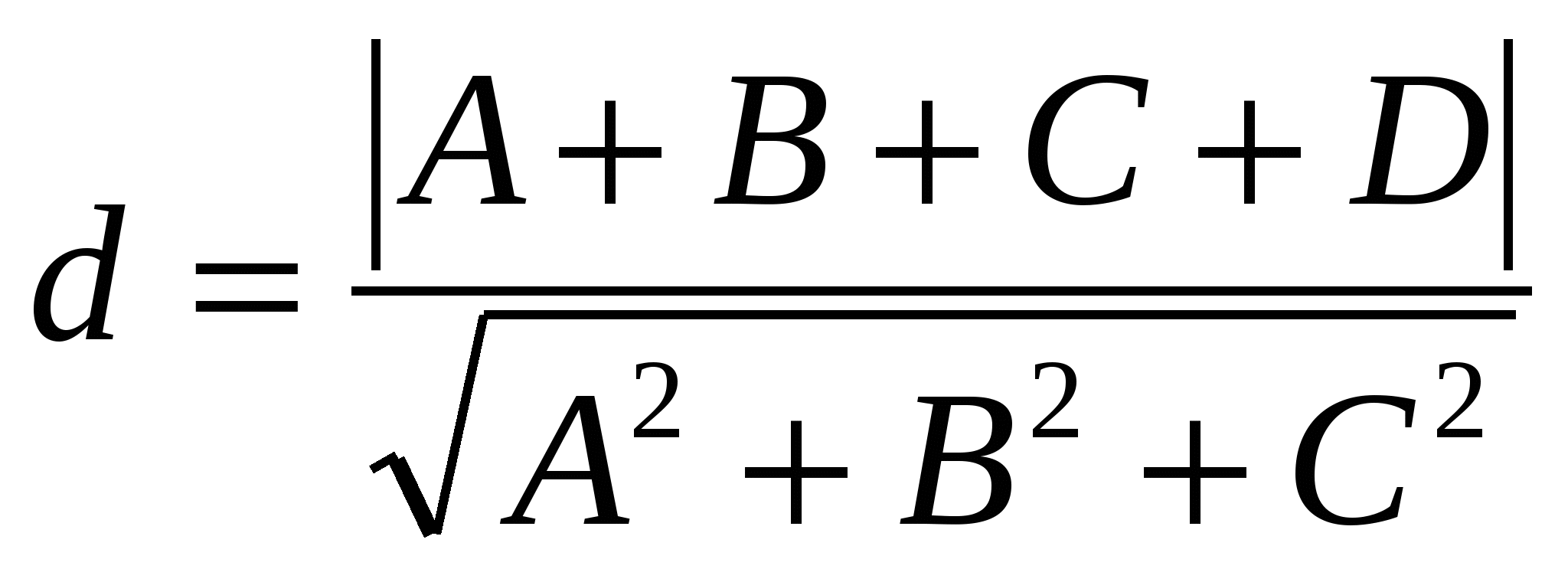
|
|
Для плоскости
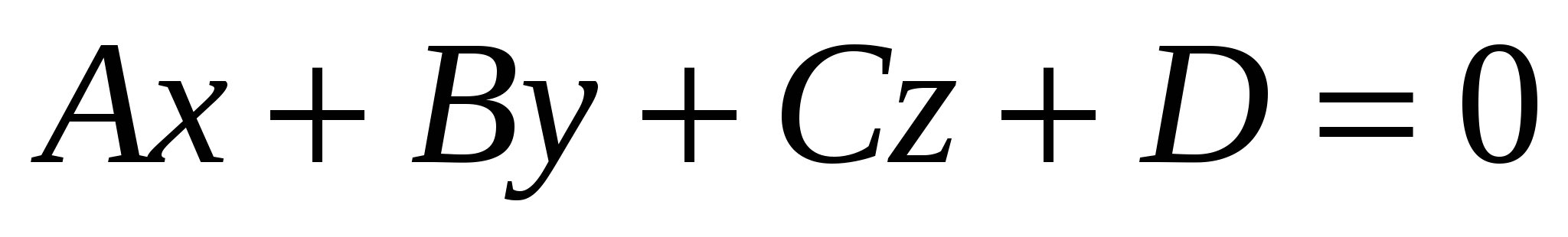
нельзя составить уравнение "в отрезках", если …
|
1. A = 0 2. D = 0
3. A 0 4. A + B + C = 0
|
|
Заданы канонические уравнения прямой в пространстве:
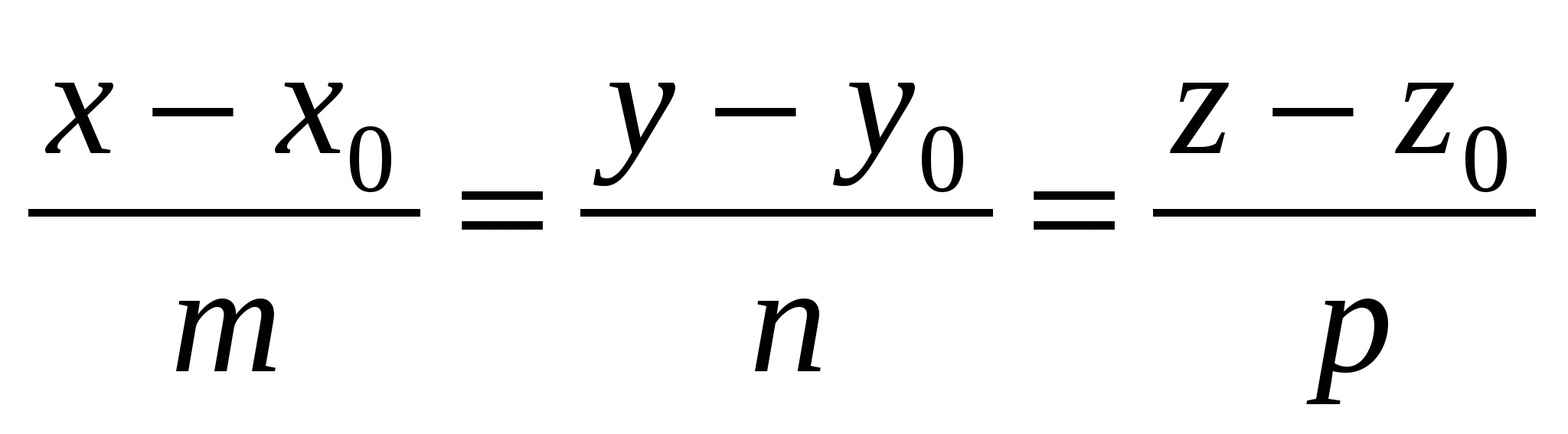 , ,
тогда эта прямая …
|
1. Проходит через точку M(xo, yo, zo)
2. Проходит через точку M(m, n, p)
3. Проходит через точку M(p, n, m)
4. Проходит через начало координат
|
|
Указать параметрические уравнения прямой, проходящей через точку
M(xo, yo, zo),
и параллельной вектору
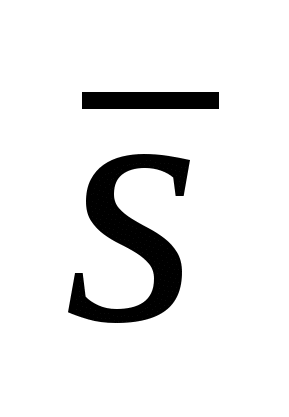 = { m; n; p}: = { m; n; p}:
|
1. 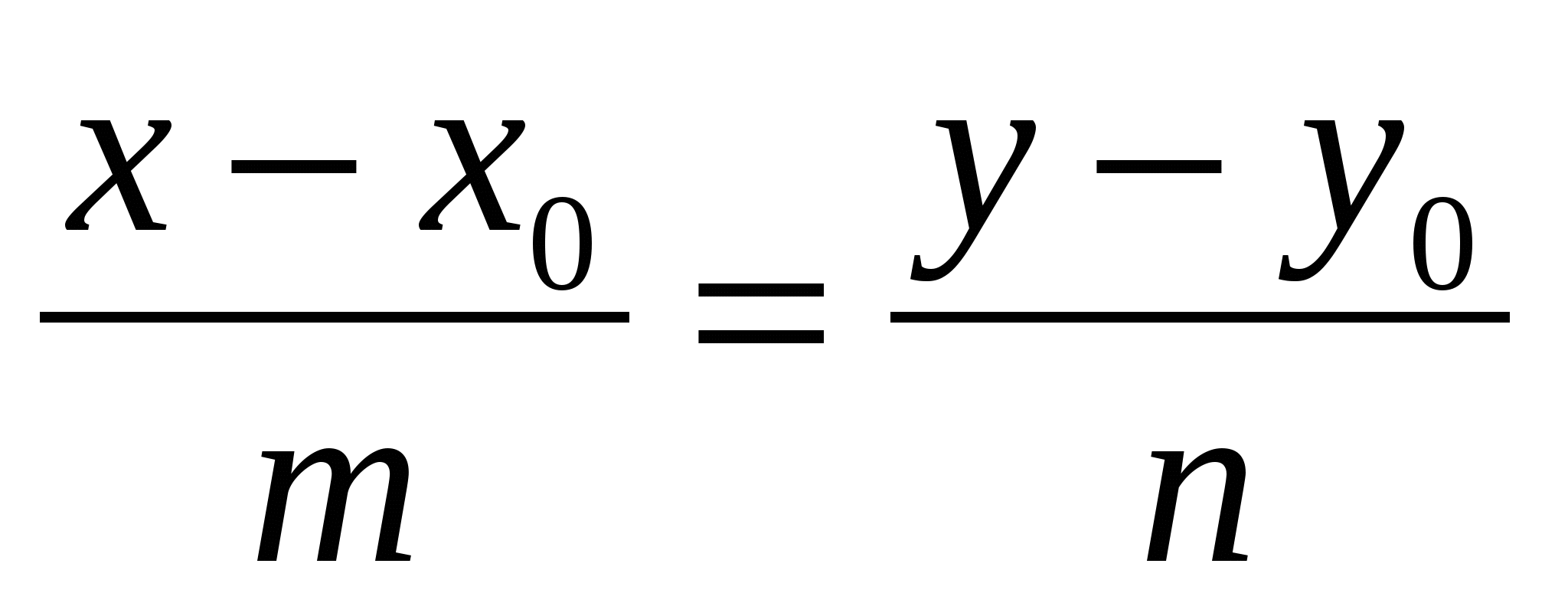
2. . x = xo t m , y = yo t n , z = zo t p
3. x = mt + xo, y = nt + yo, z = pt + zo
4. x = mt xo, y = nt yo, z = pt zo
|
|
Условие перпендикулярности двух прямых
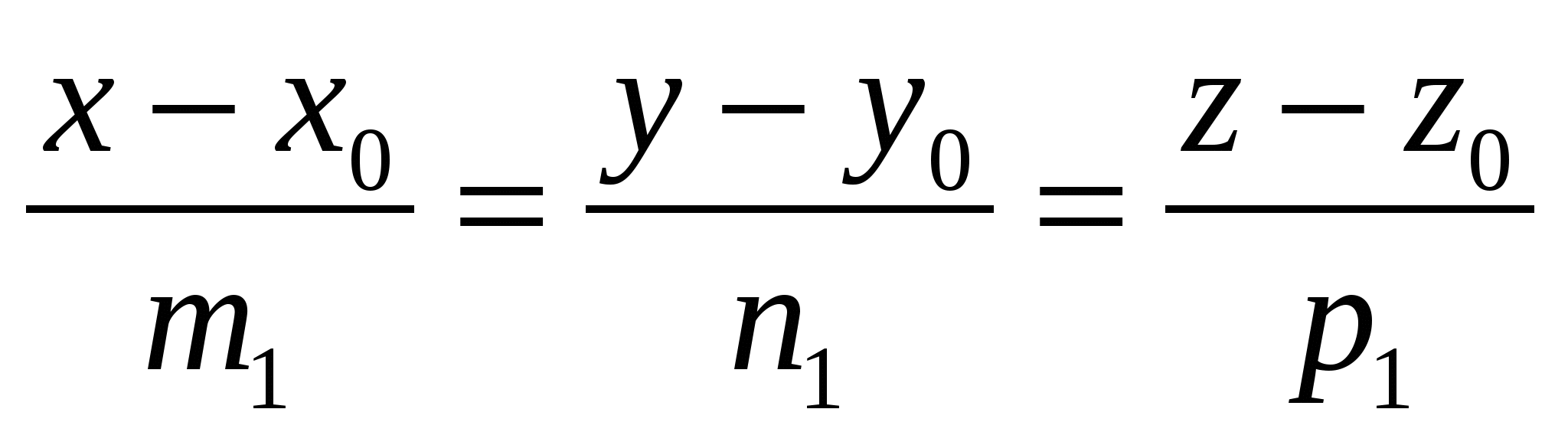 и и
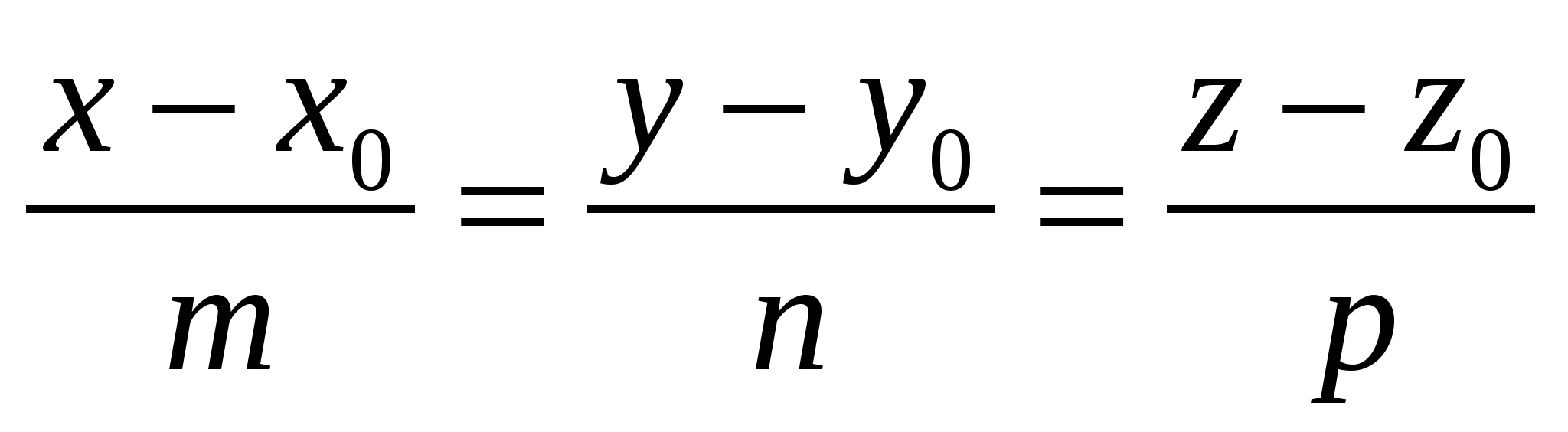
в пространстве:
|
1. 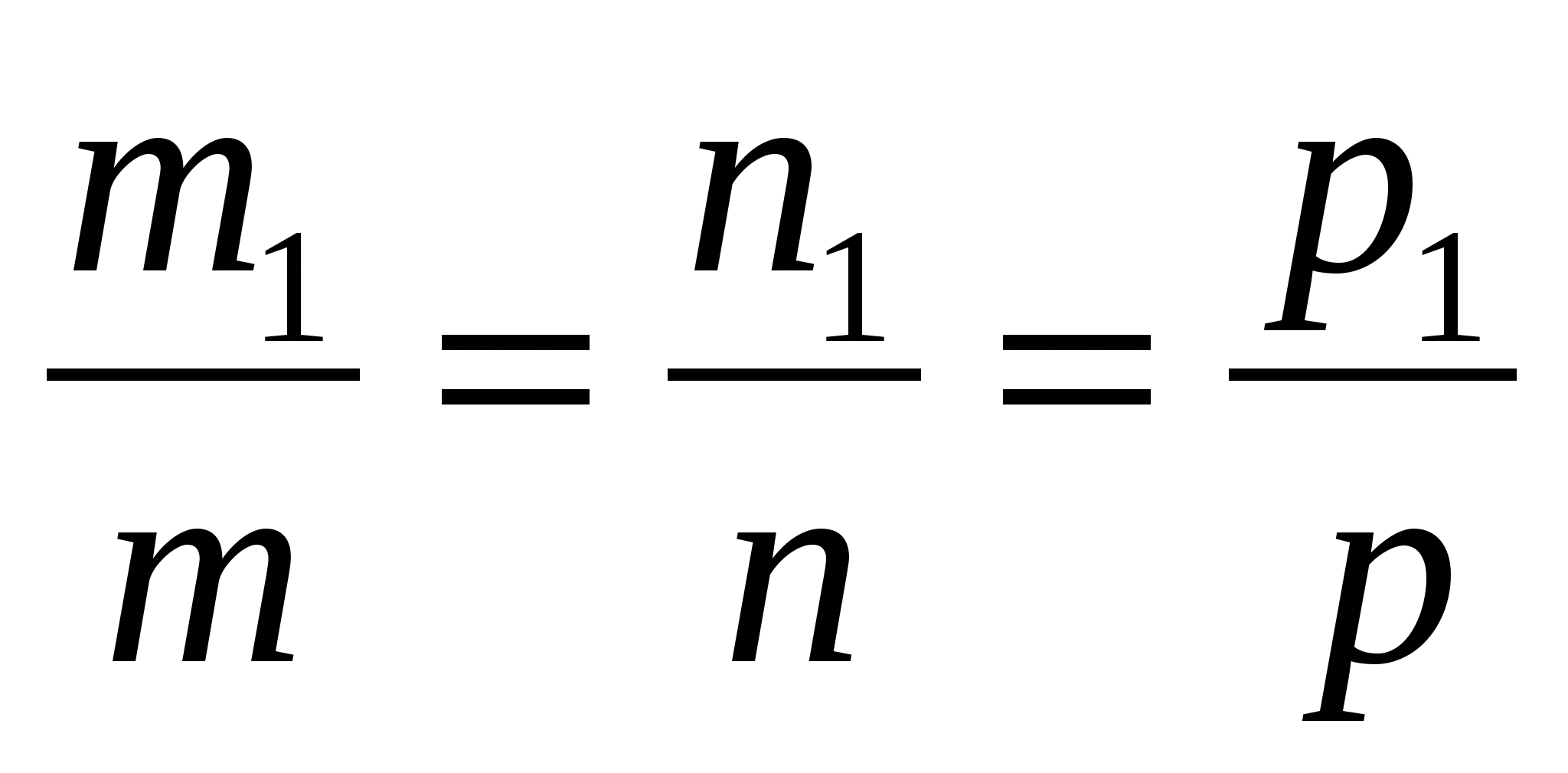
2. 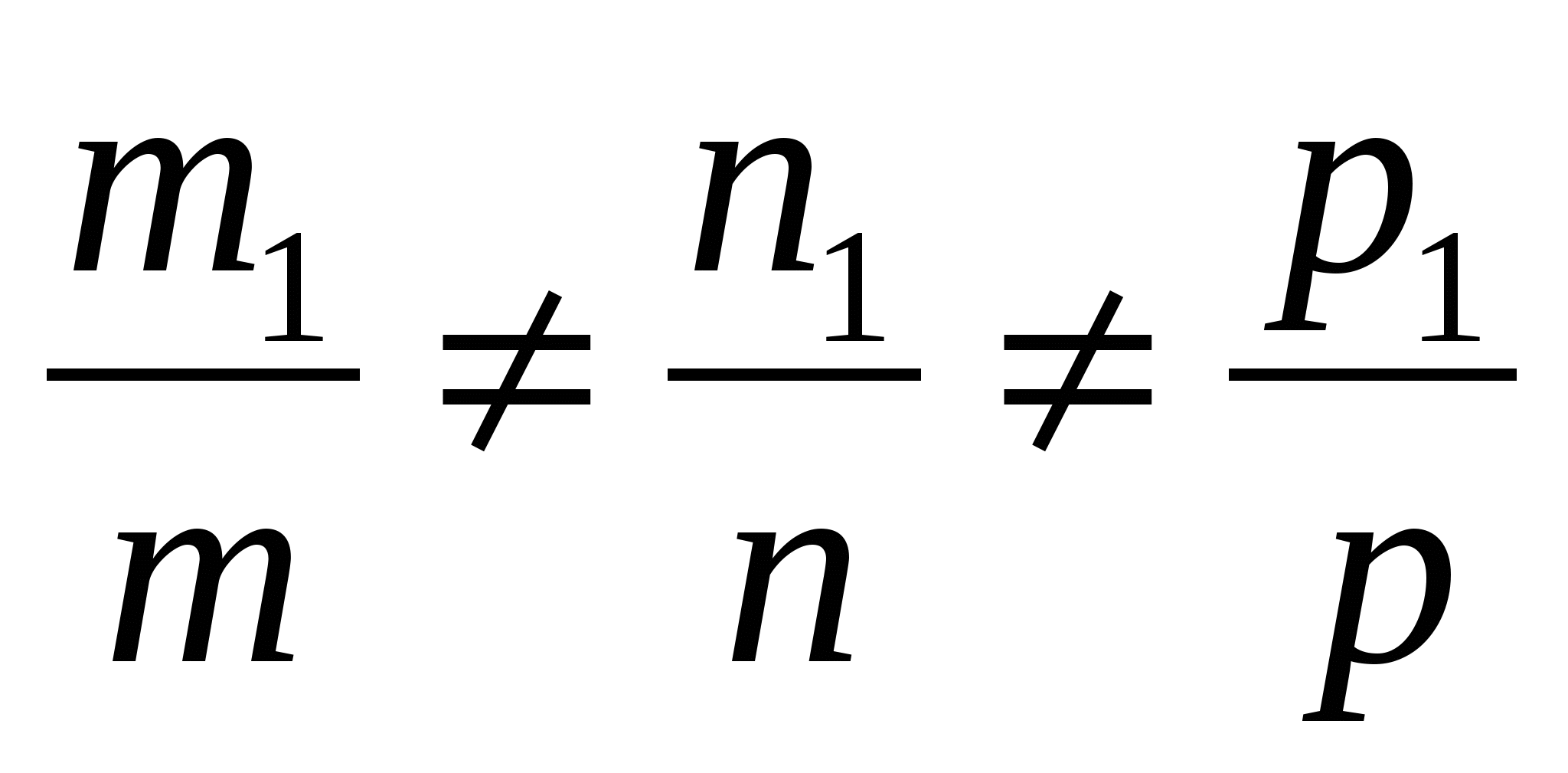
3. 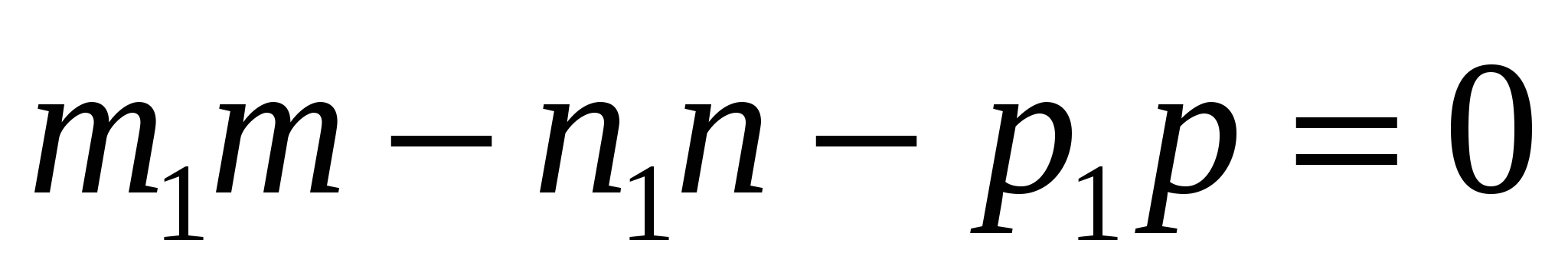
4. 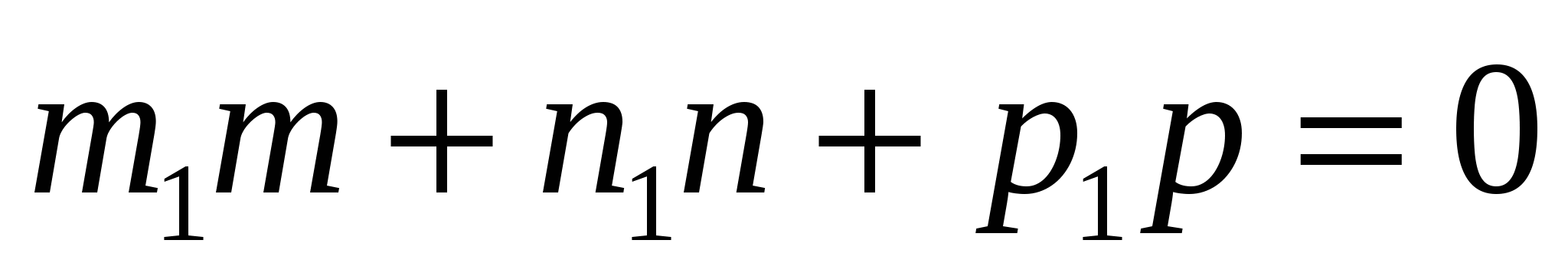
|
|
Условие параллельности двух прямых
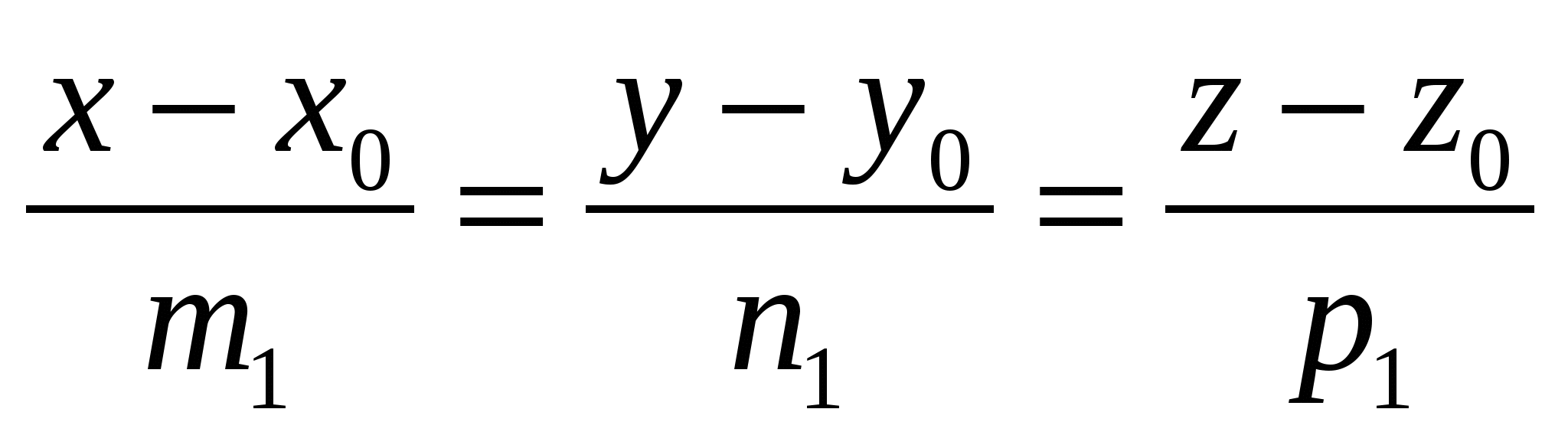 и и
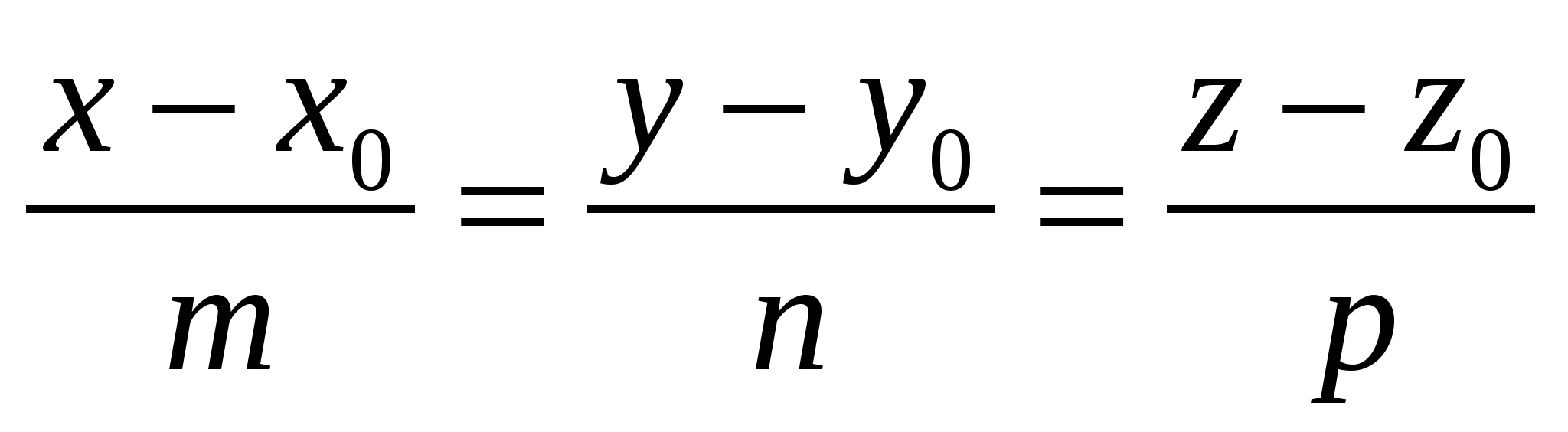
в пространстве:
|
1. 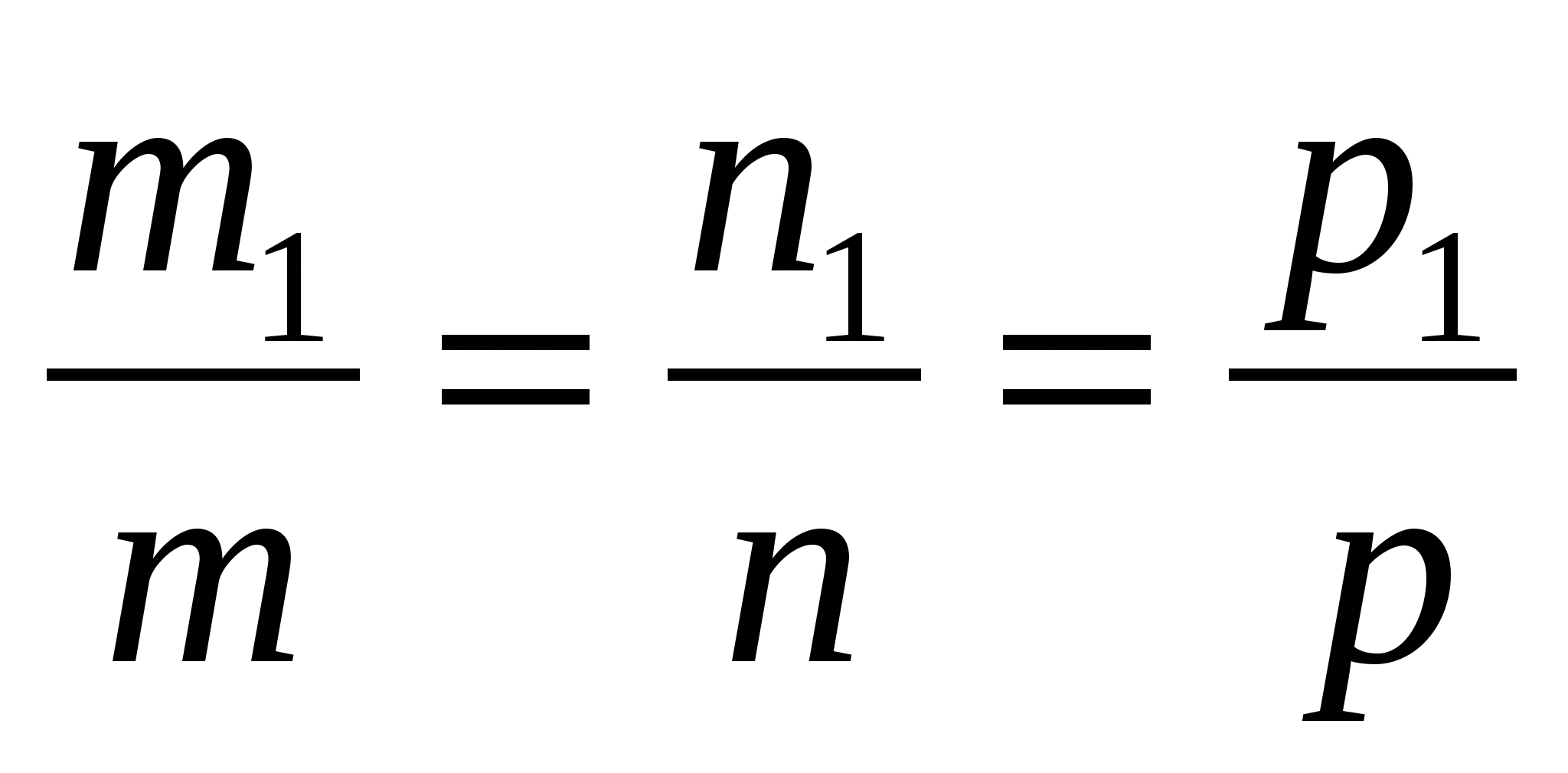
2. 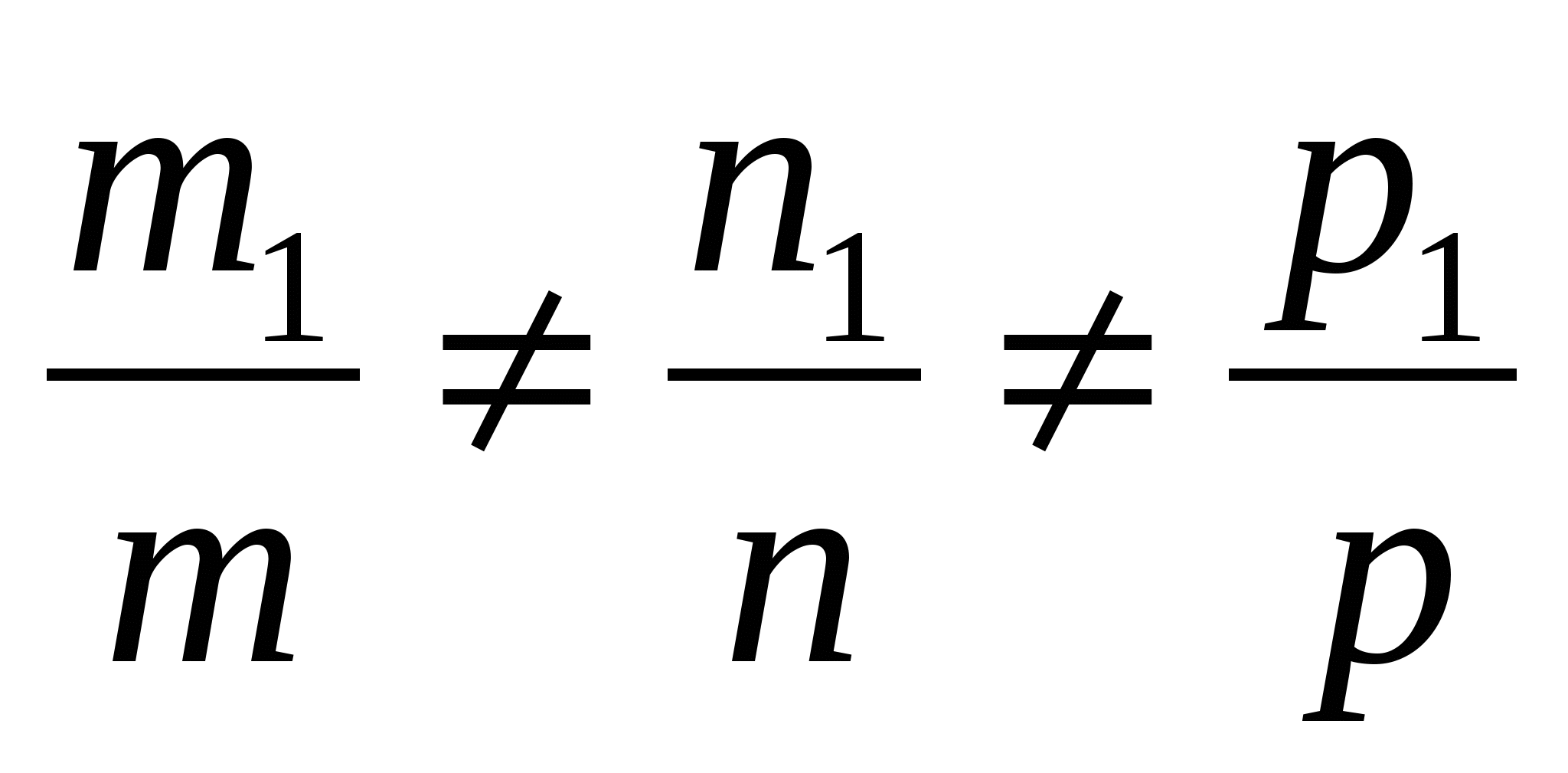
3. 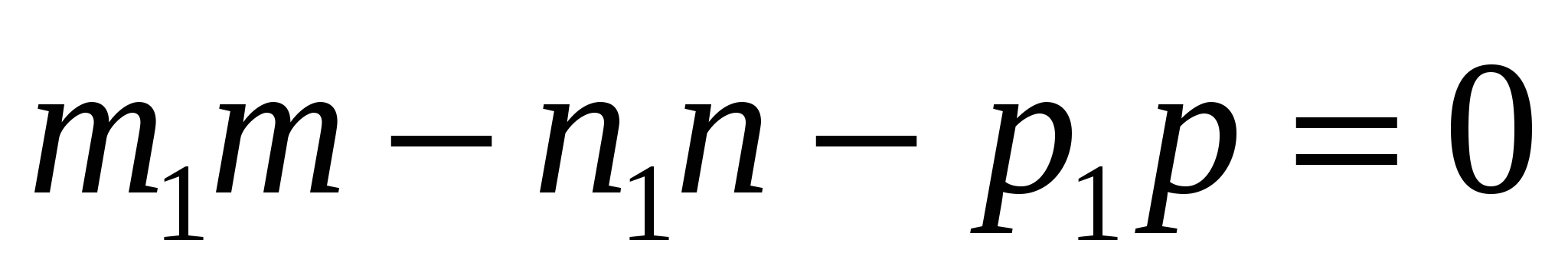
4. 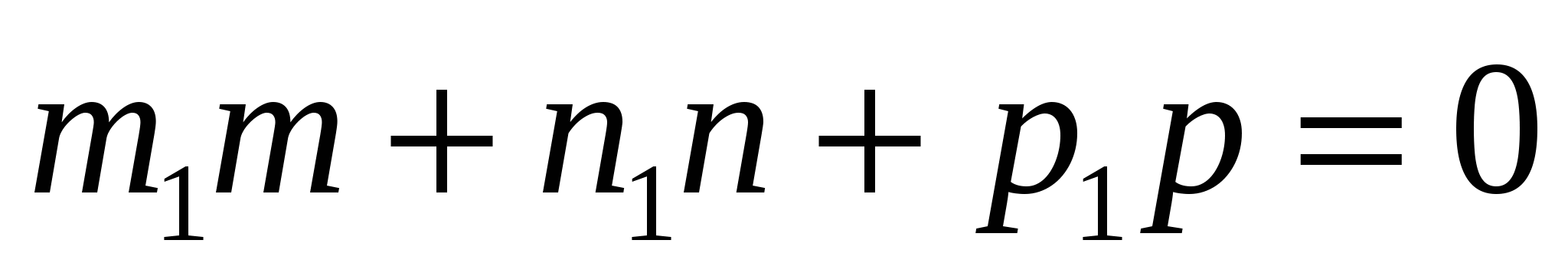
|
|
Уравнения прямой, проходящей через две заданные точки 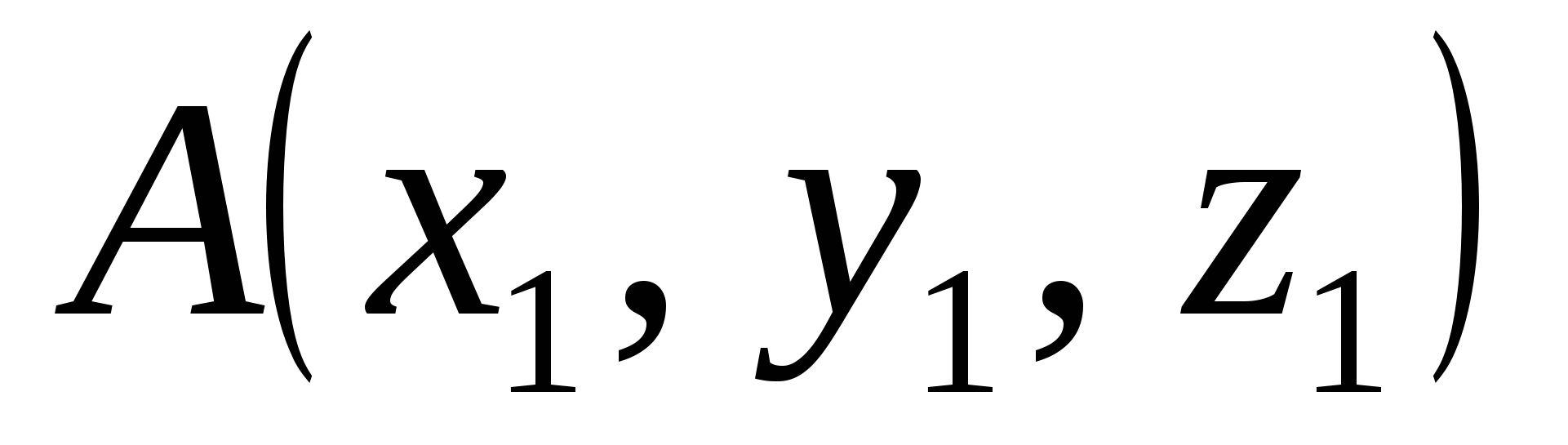 и и 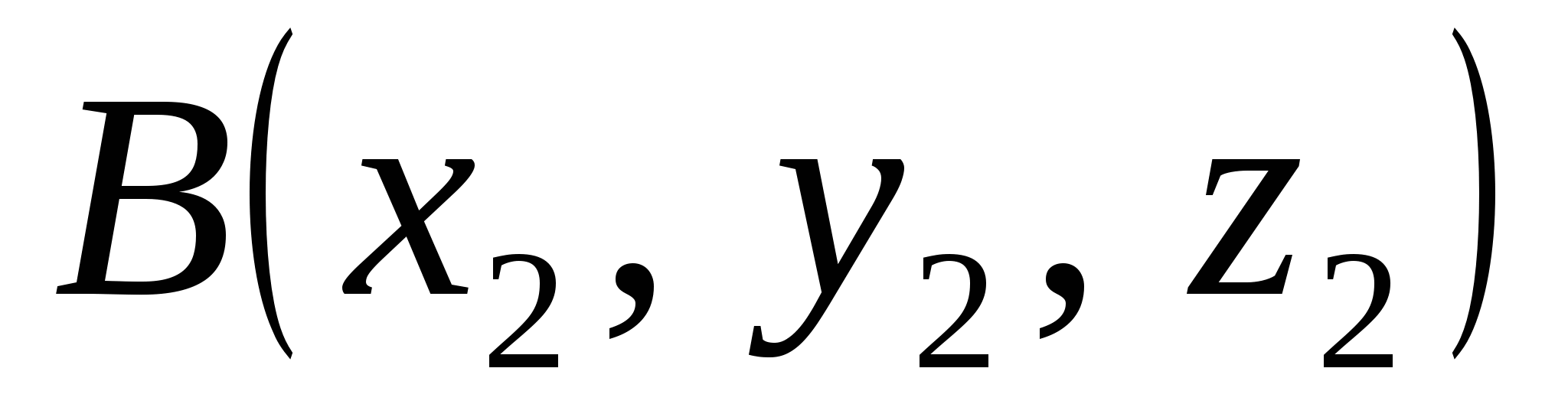 , имеют вид: , имеют вид:
|
1. 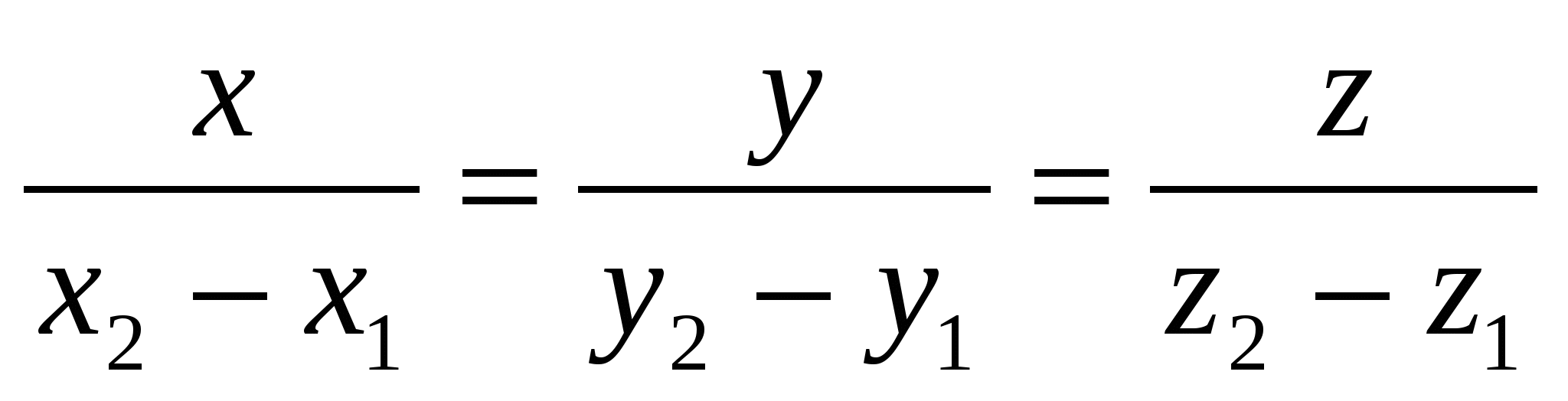
2. 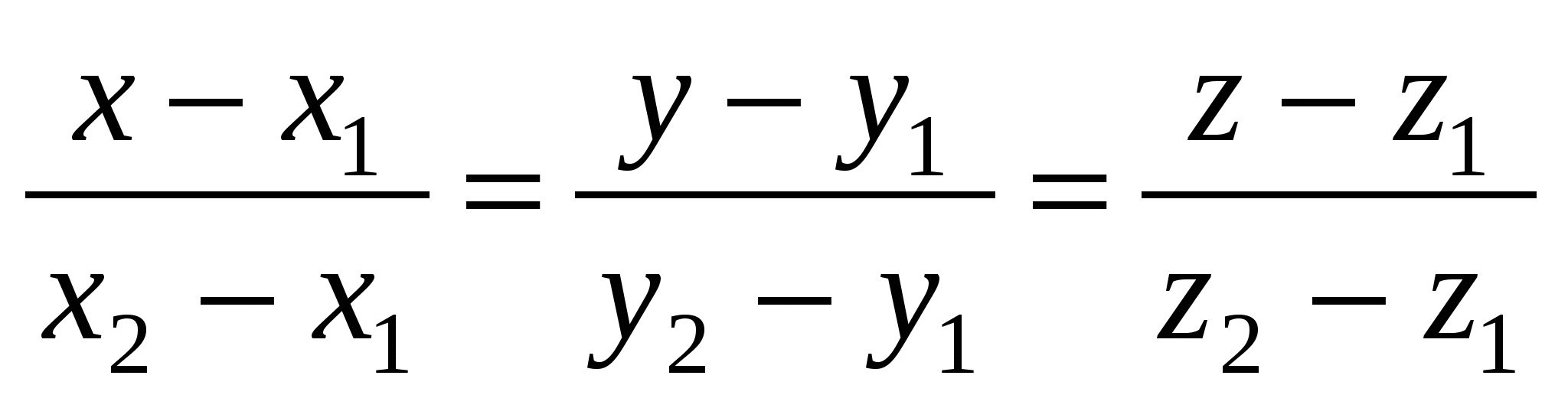
3. 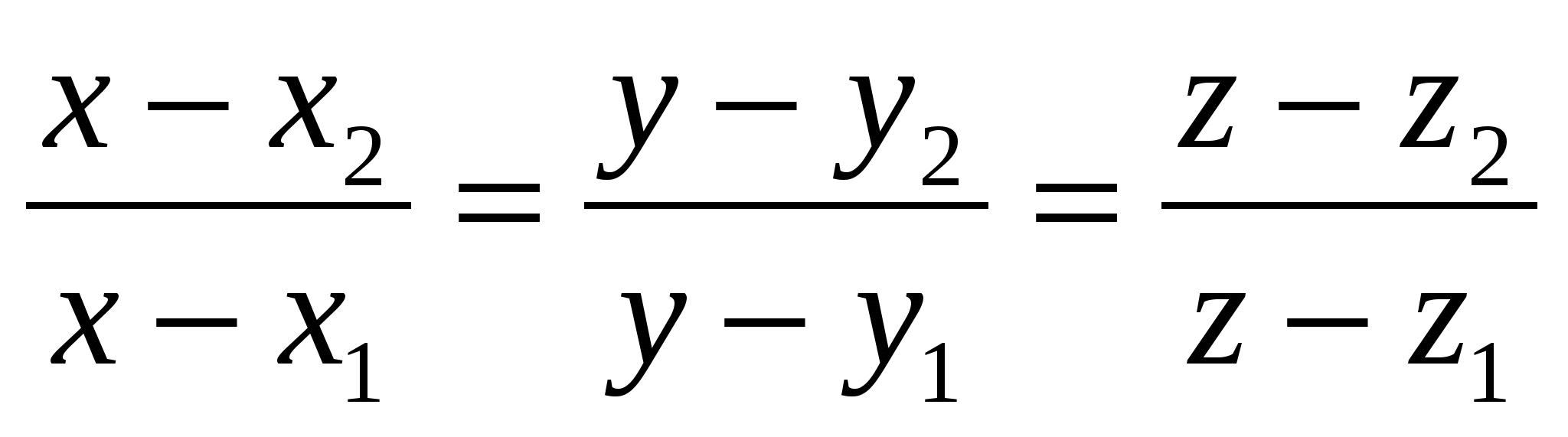
4. В пп. 13 нет правильного ответа
|
|
Какая из заданных прямых параллельна прямой
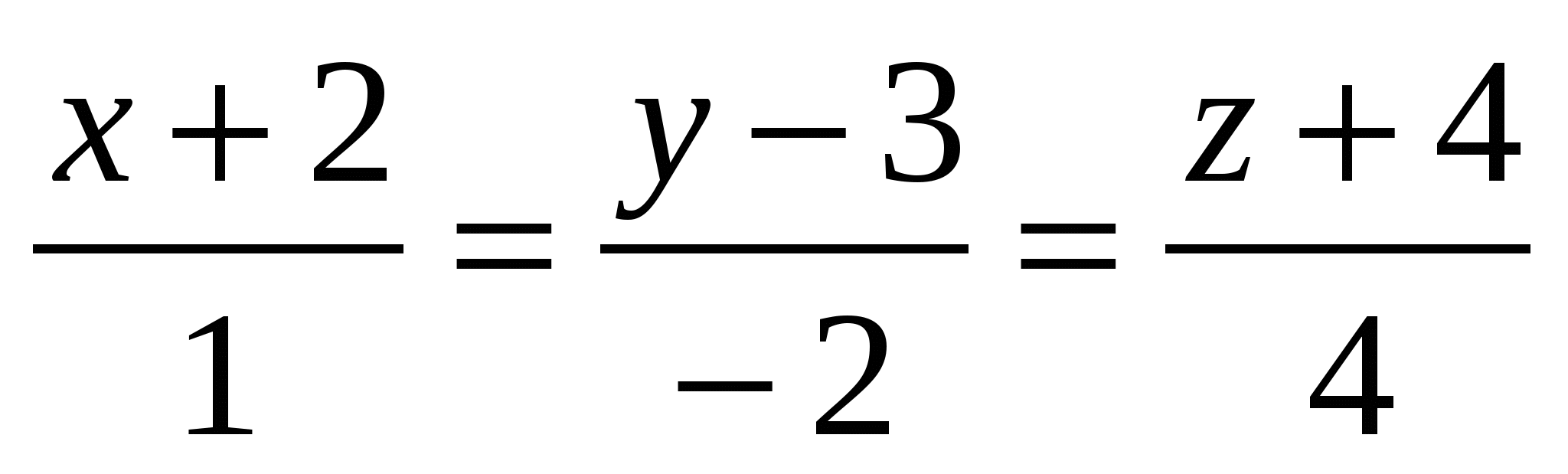 : :
|
1. x = t + 2, y = t 5, z = t + 4
2. x = 2 t + 2, y = 4 t 5, z = 8 t + 3
3. x = t + 2, y = 3 t 5, z =4 t + 3
4. x = 40 t + 2, y = 3t, z = –7t + 3
|
|
В пространстве Охуz уравнения
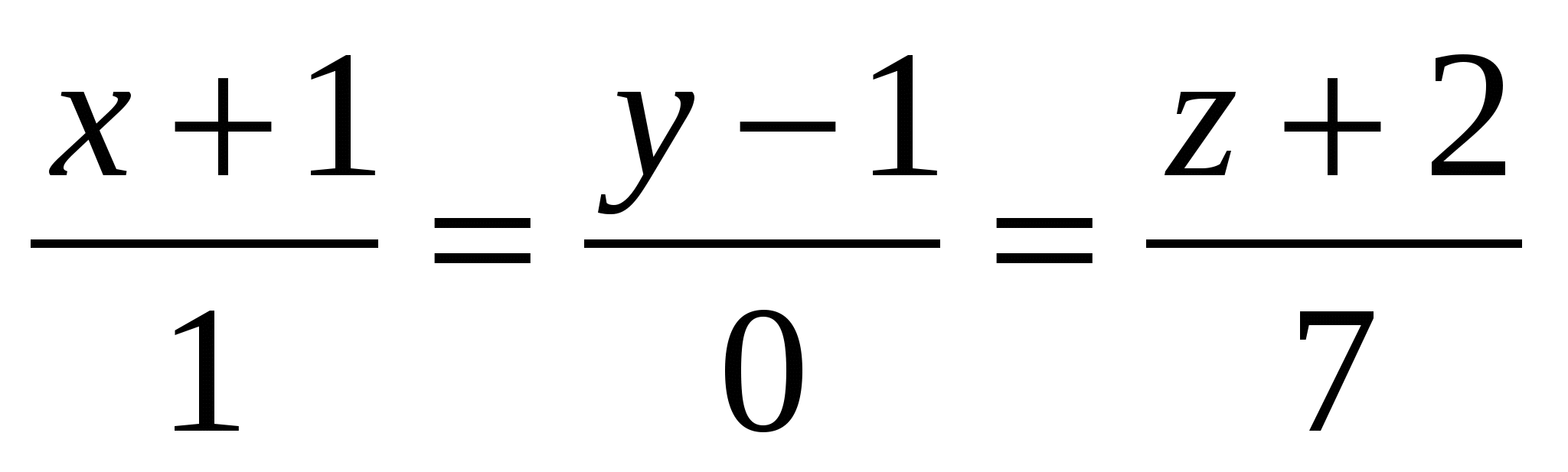
определяют:
|
1. Прямую, перпендикулярную оси Оу
2. Плоскость, перпендикулярную оси Оу
3. Прямую, параллельную оси Оу
4. уравнения не имеют смысла, так как осуществляется деление на 0.
|
|
Какая из указанных плоскостей перпендикулярна прямой
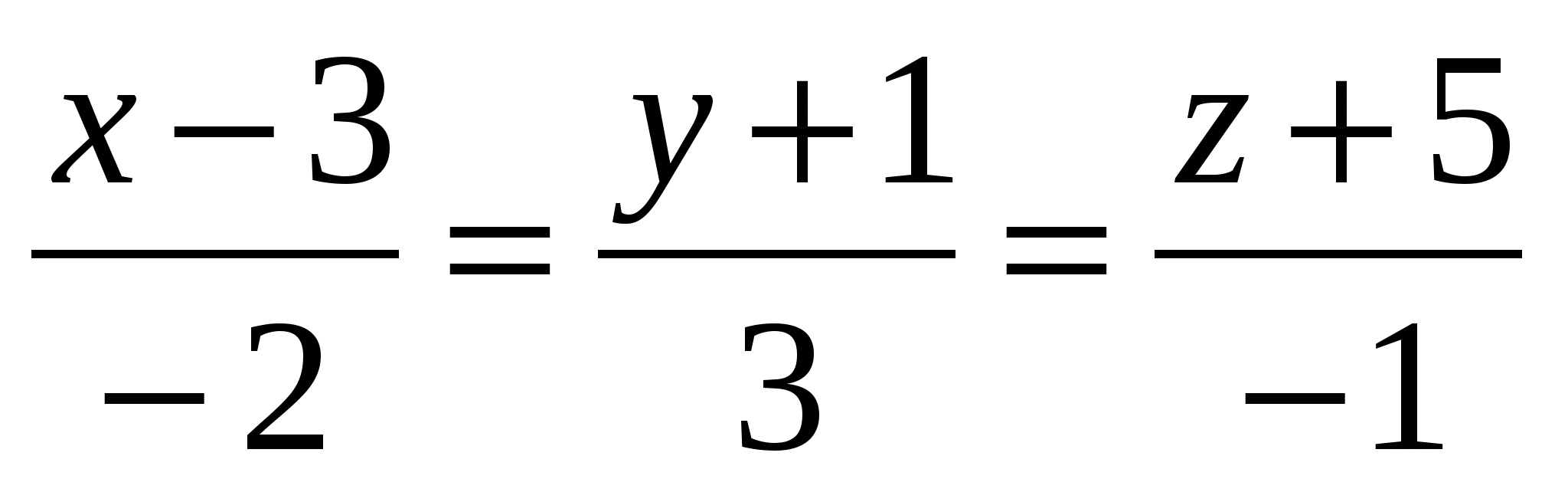 : :
|
1. 2x + 6y 3z 15 = 0
2. 4x 6y + 2z 17 = 0
3. 2x + y z 31 = 0
4. 5x + y + 3 z 27 = 0
|
|
Условие перпендикулярности прямой
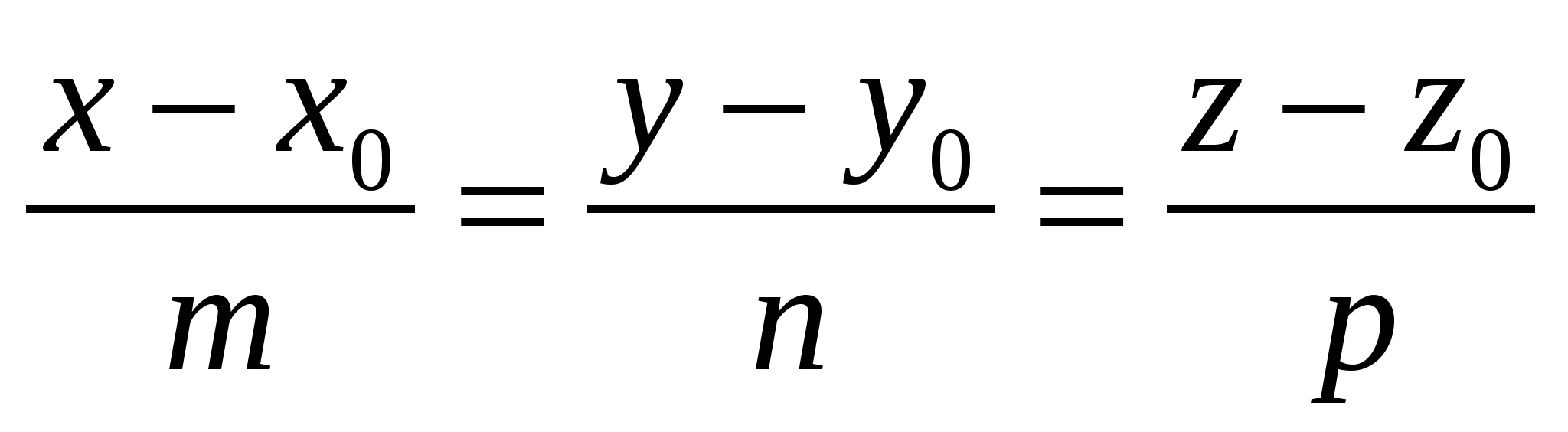
и плоскости
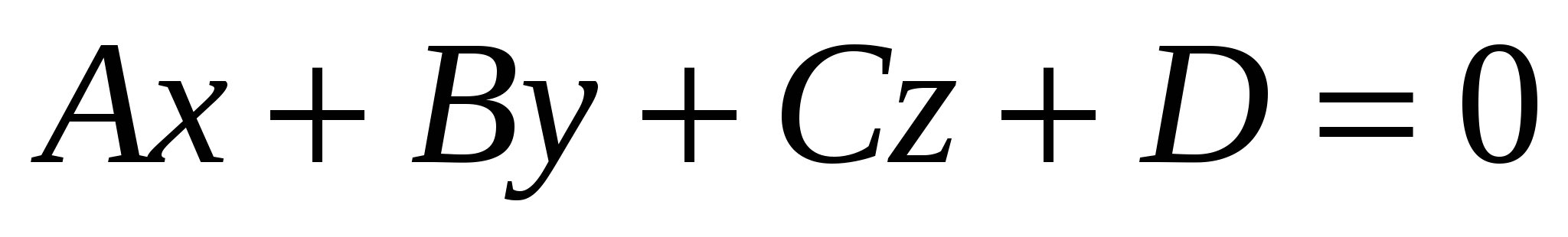 : :
|
1. 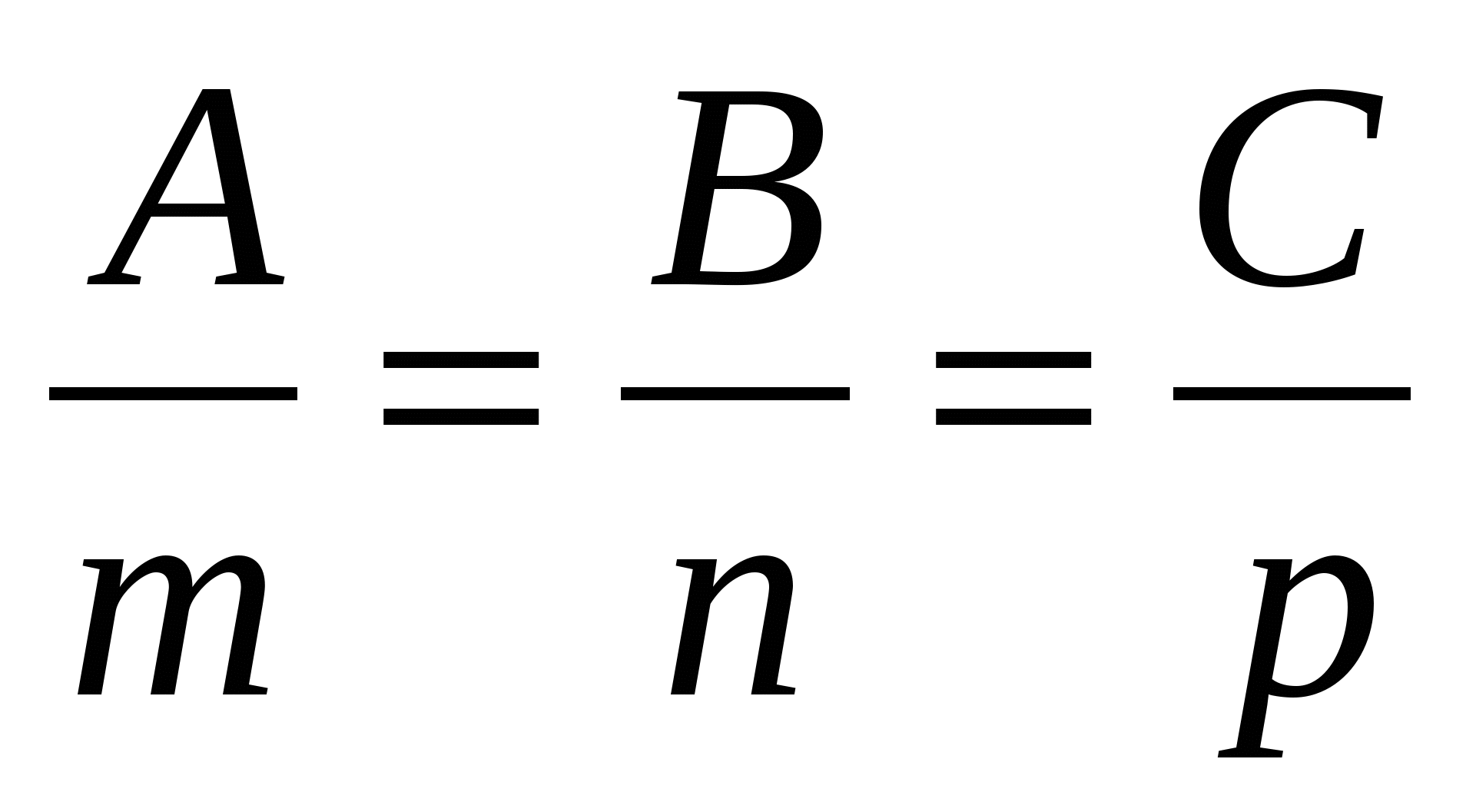
2. 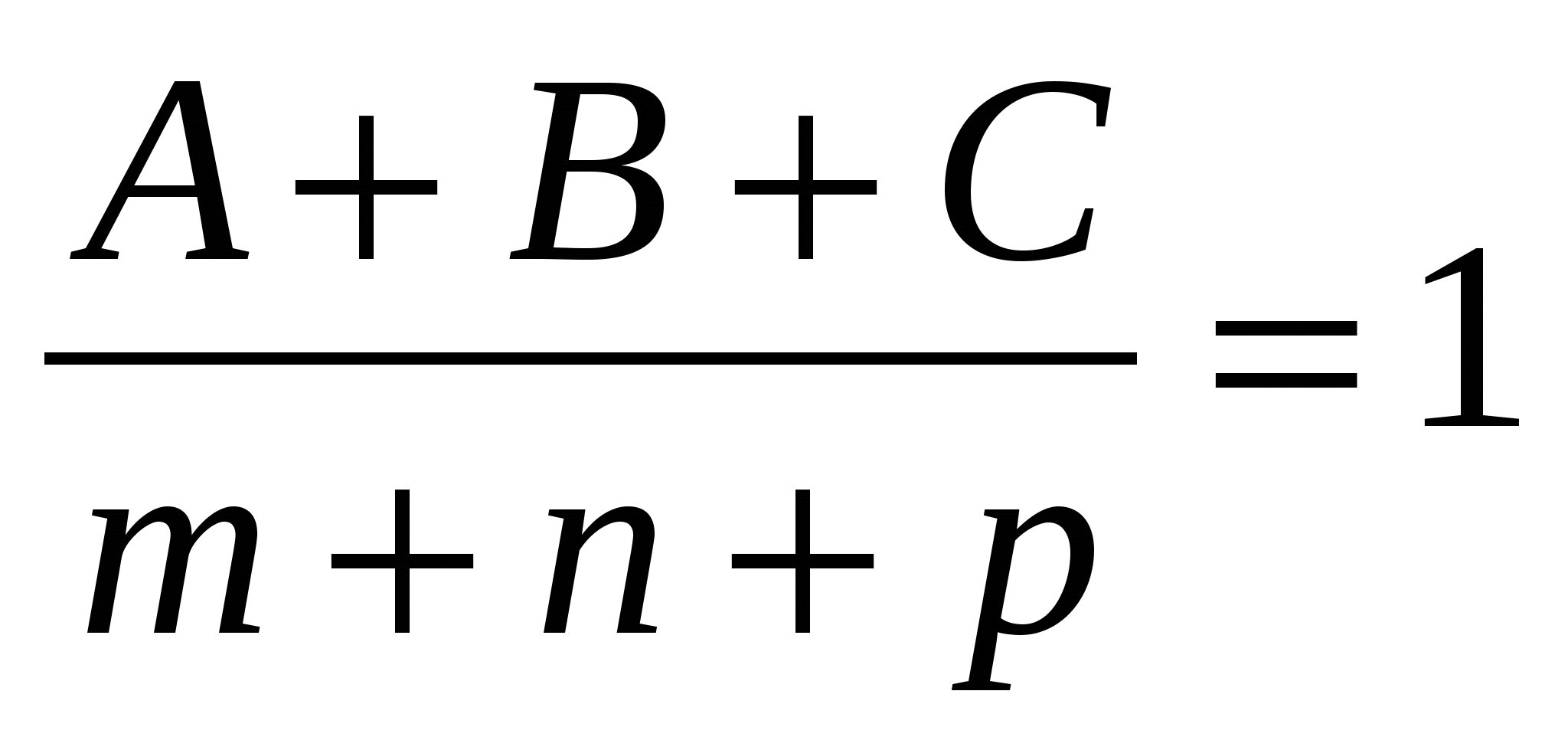
3. 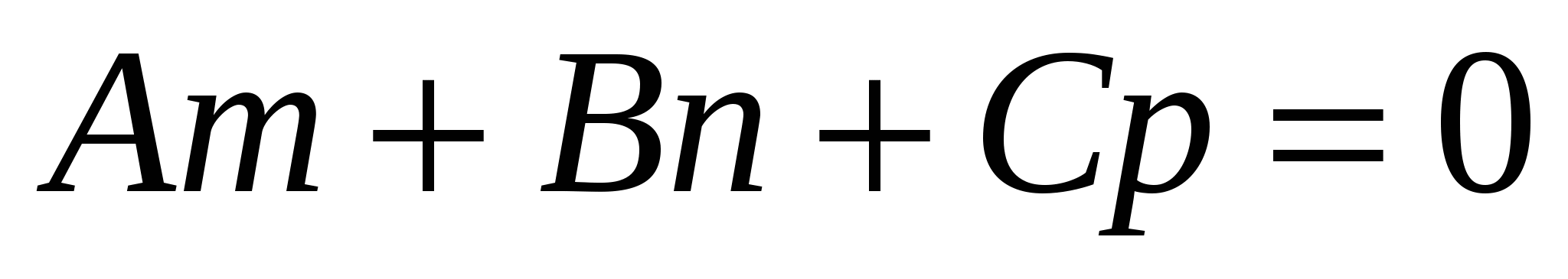
4. 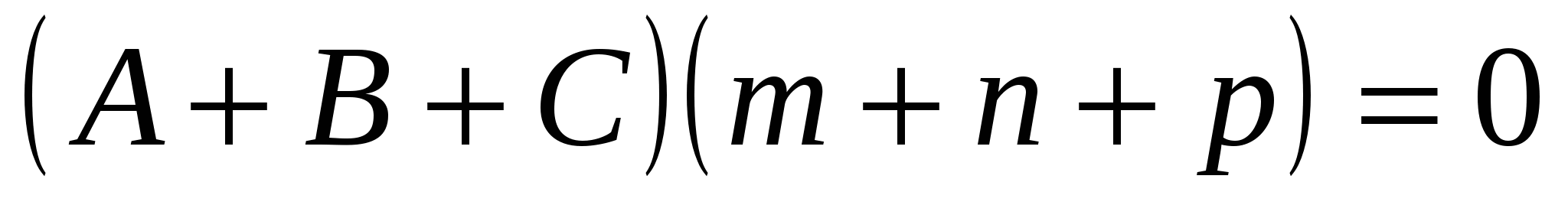
|
|
Канонические уравнения прямой, проходящей через точку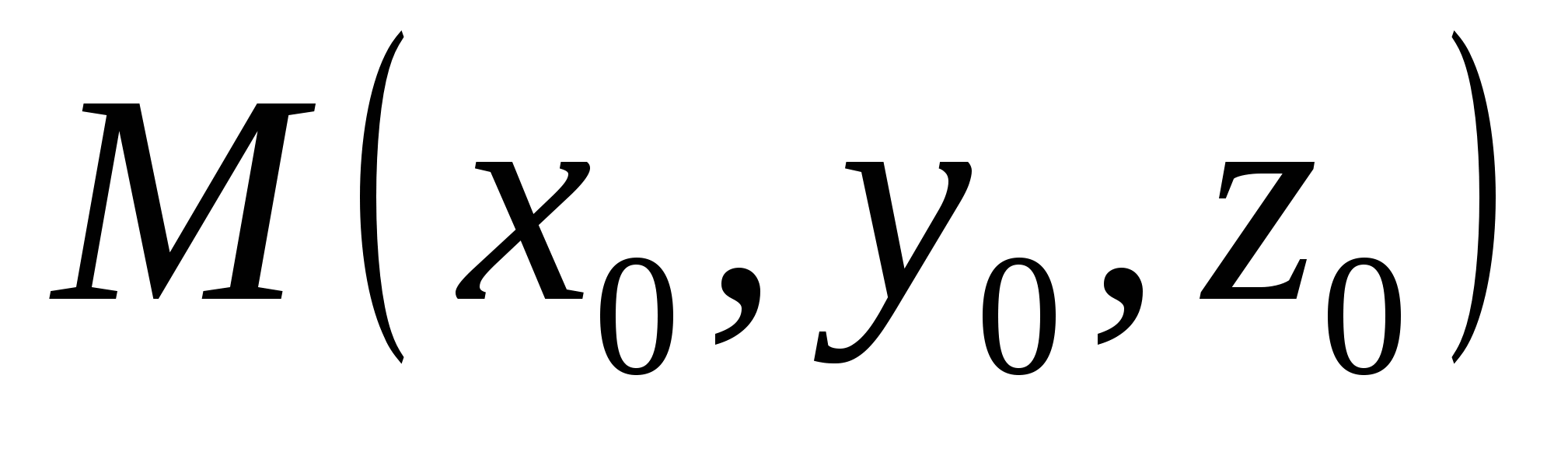 , параллельно вектору , параллельно вектору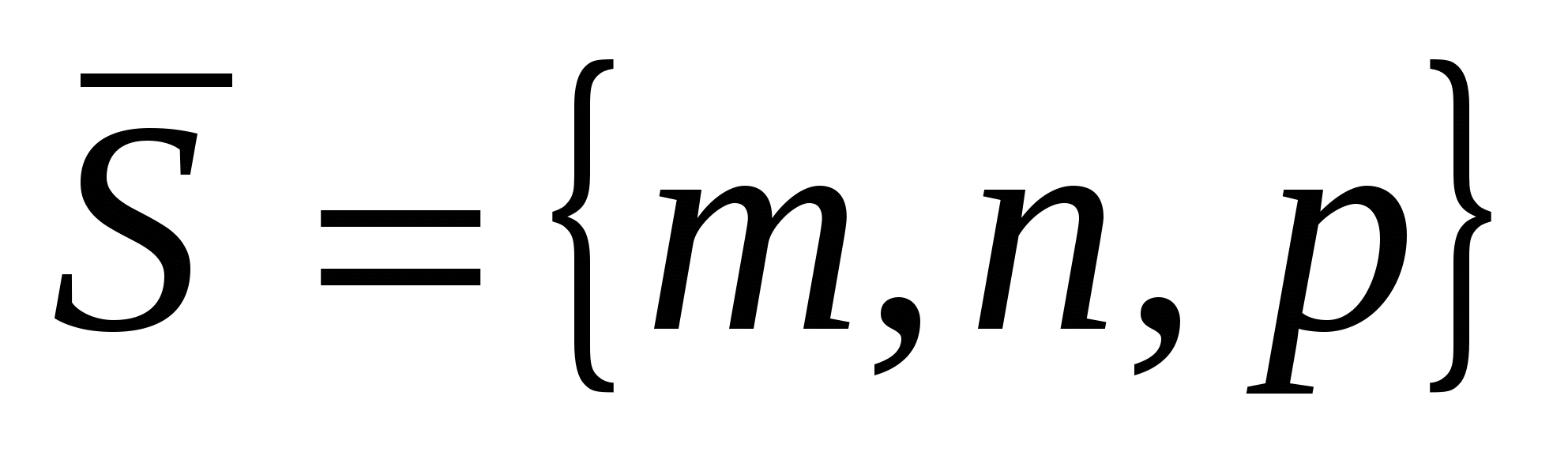 в пространстве имеют вид в пространстве имеют вид
|
1. 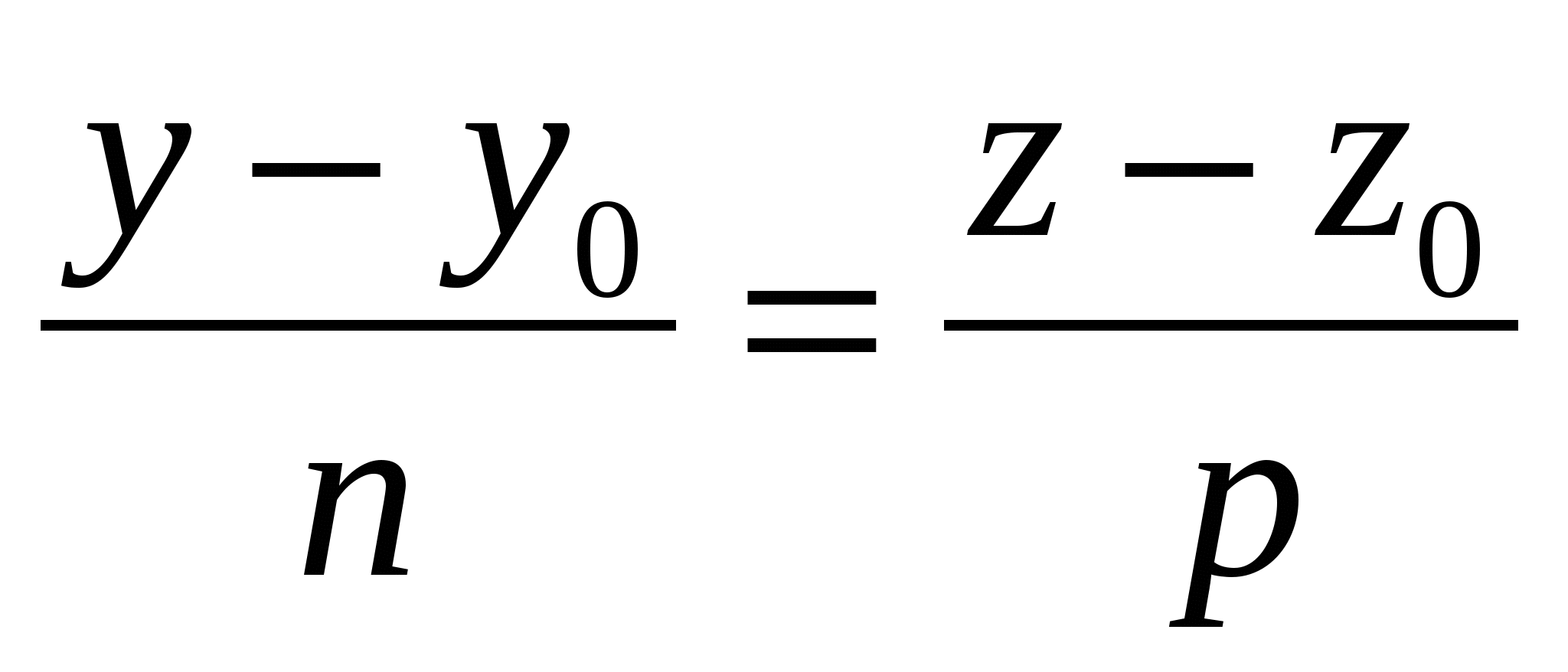
2. 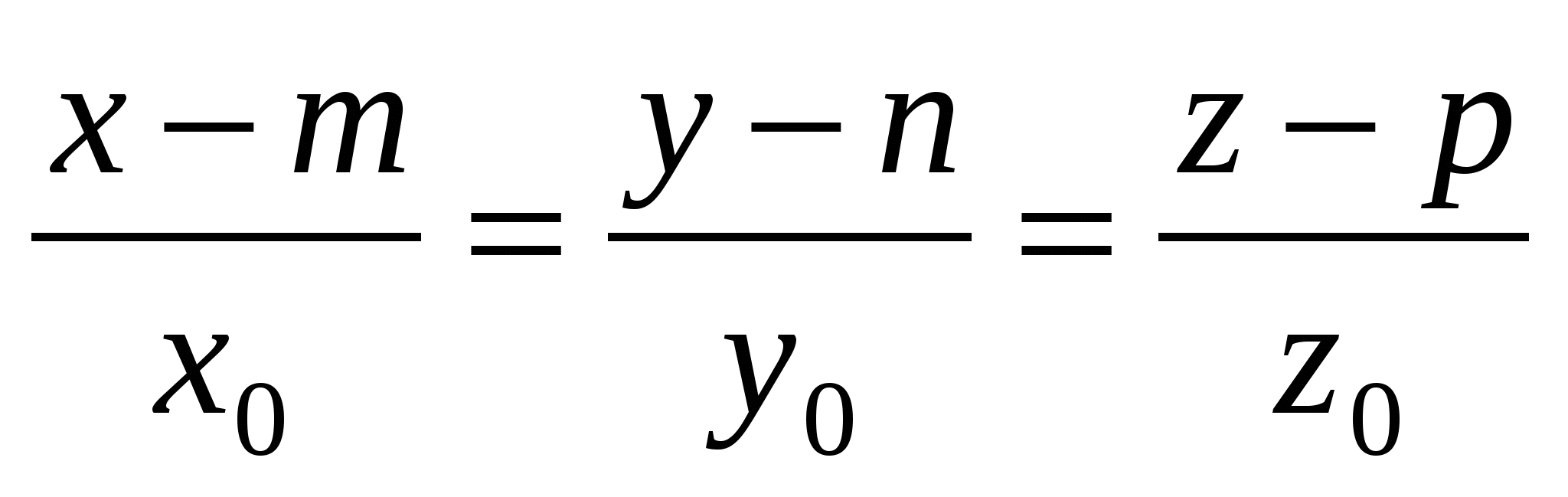
3. 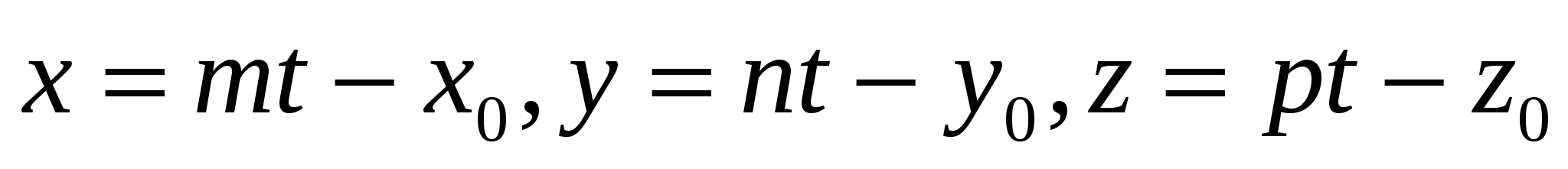
4. 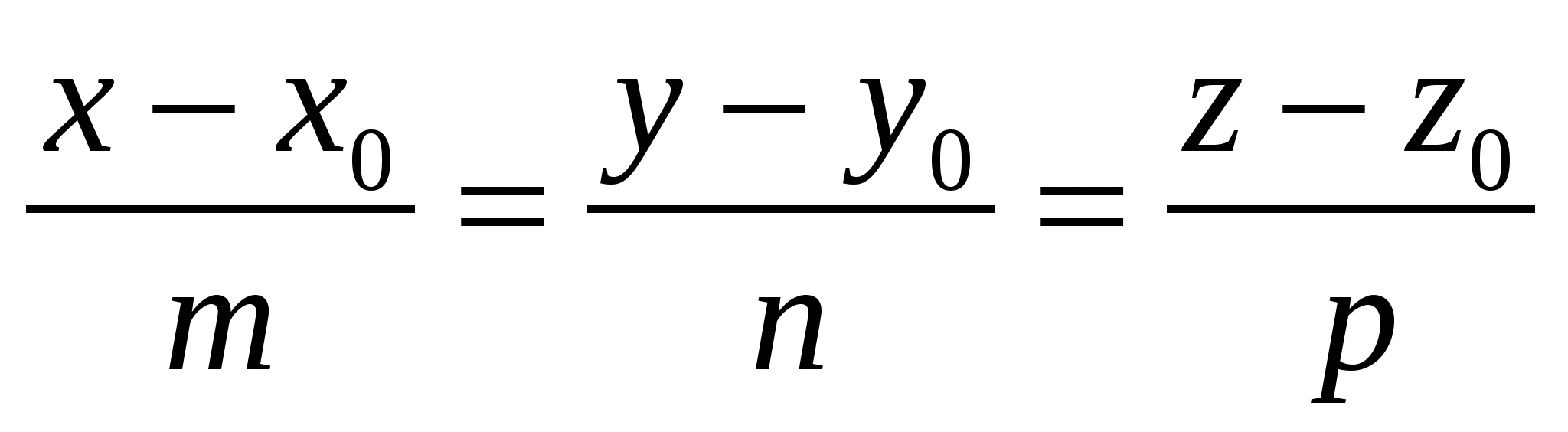
|
|
Общее уравнение плоскости имеет вид
x + 2y 3 z 6 = 0,
тогда ее уравнение в отрезках …
|
1. x ∕ 6 y∕3 + z ∕ 2 = 0 2. x + 2y 3 z = 18
3. 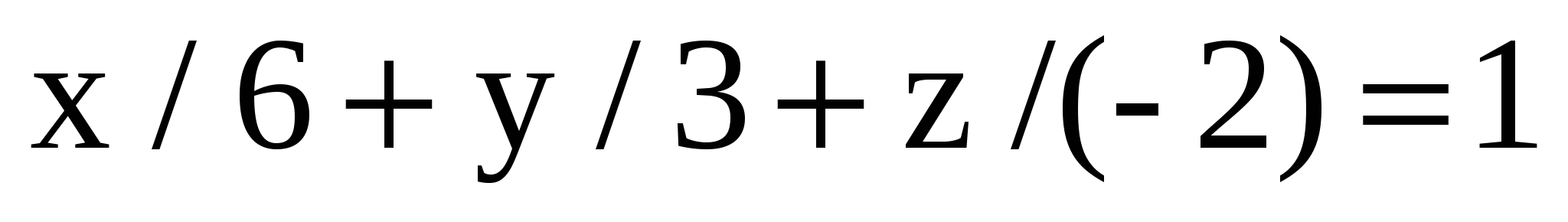 4. x + 2y 3 z = 0 4. x + 2y 3 z = 0
|
|
Расстояние от точки 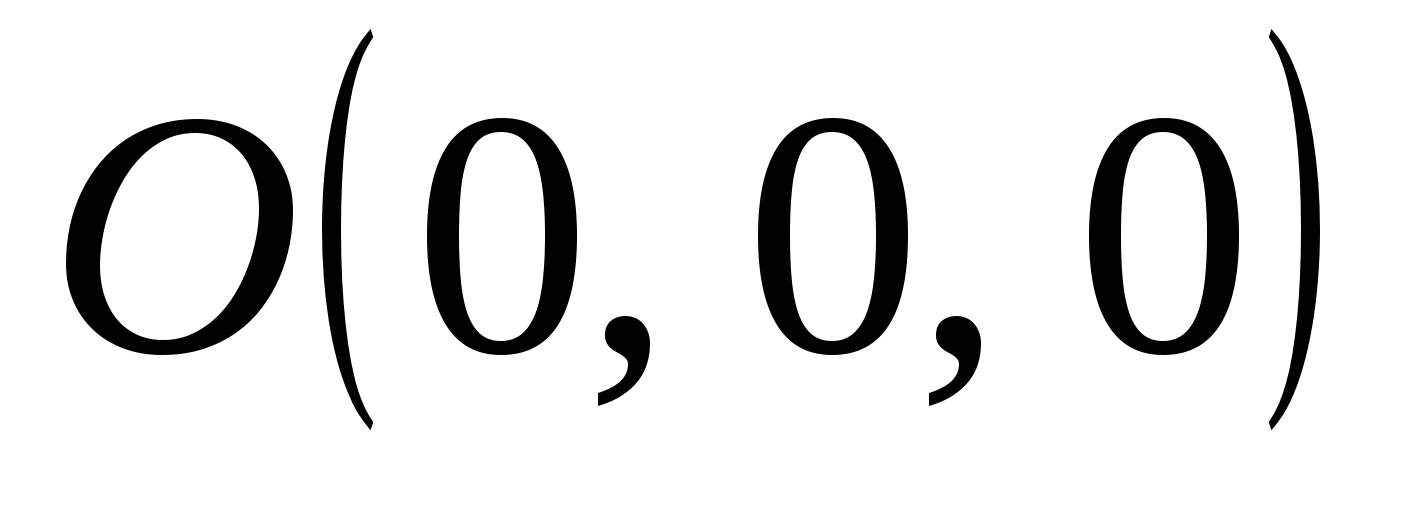 до плоскости до плоскости 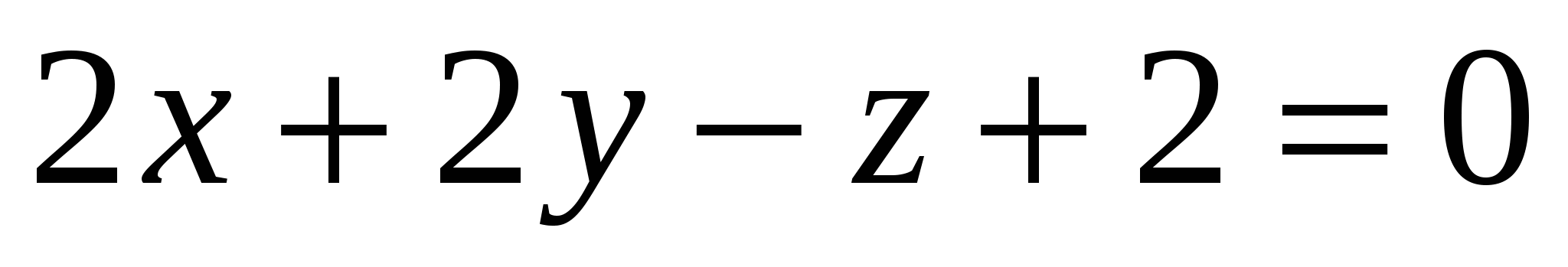 равно равно
|
1. 2 2. 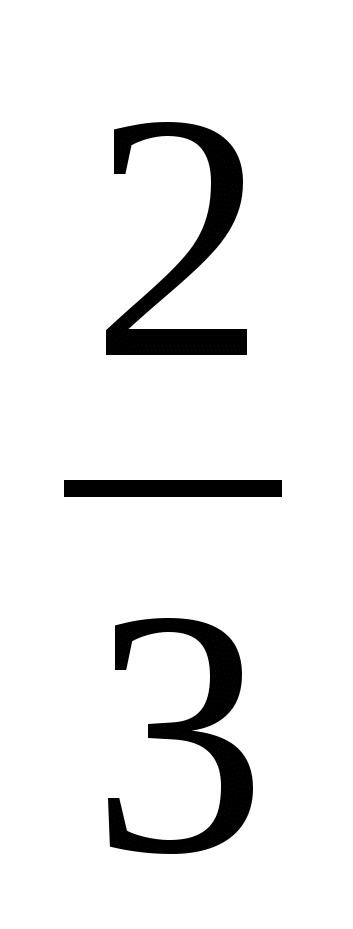 3. 1 4. 3. 1 4. 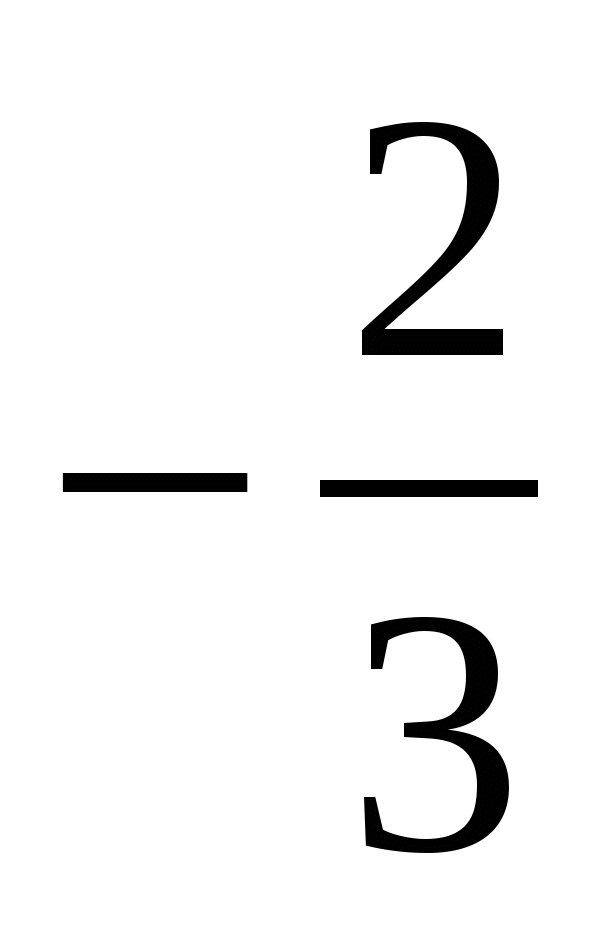
|
|
Условие параллельности прямой
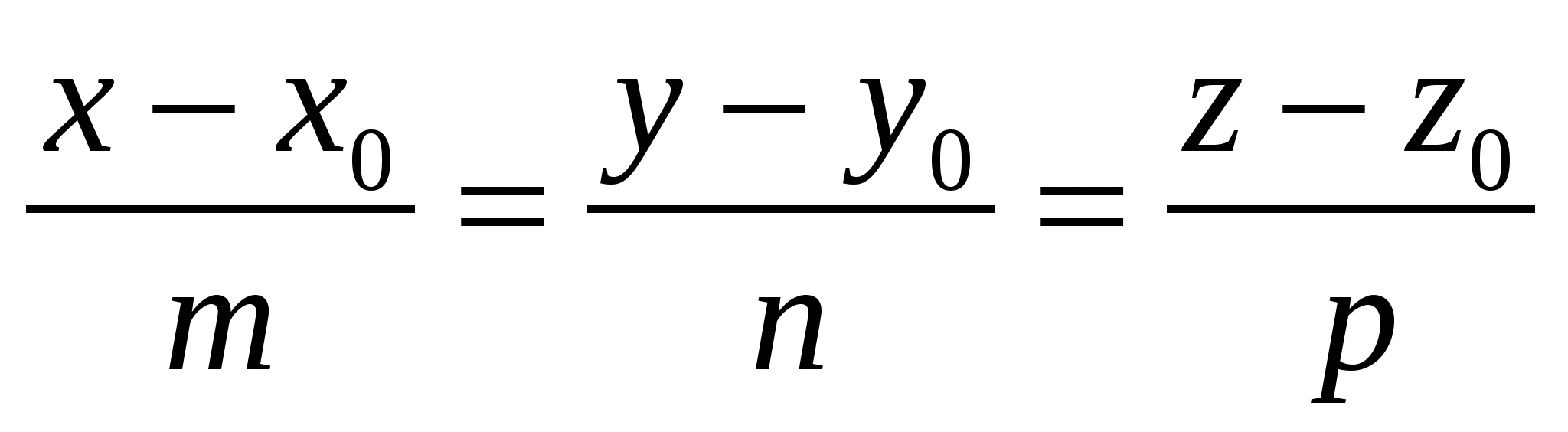
и плоскости
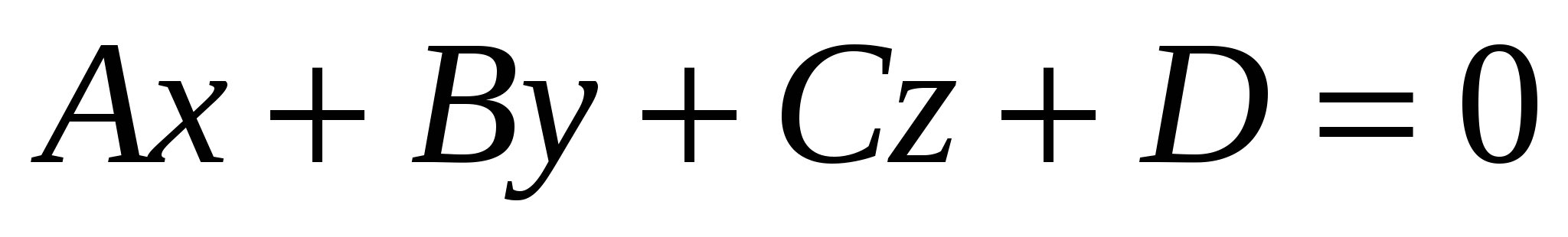 : :
|
1. 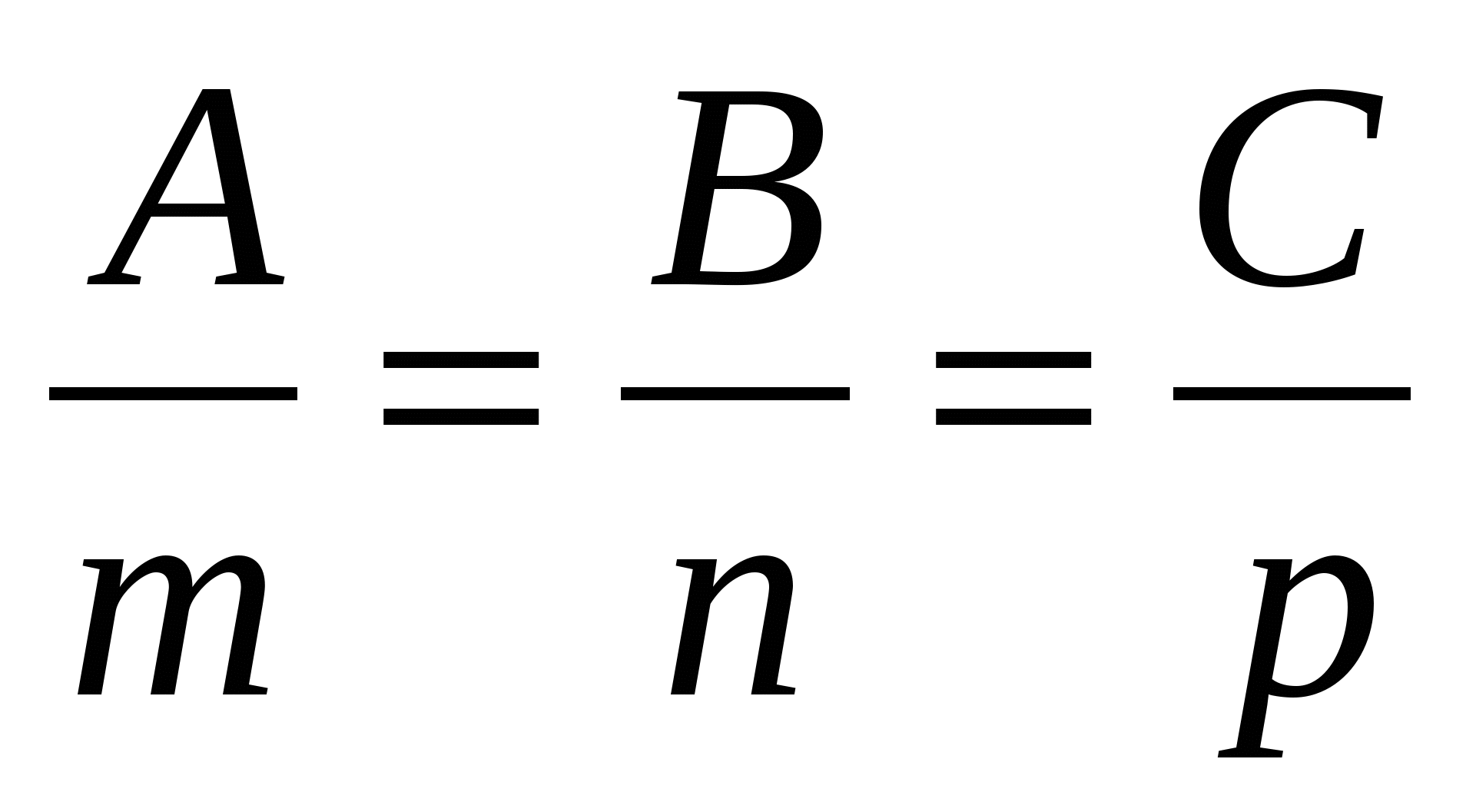
2. 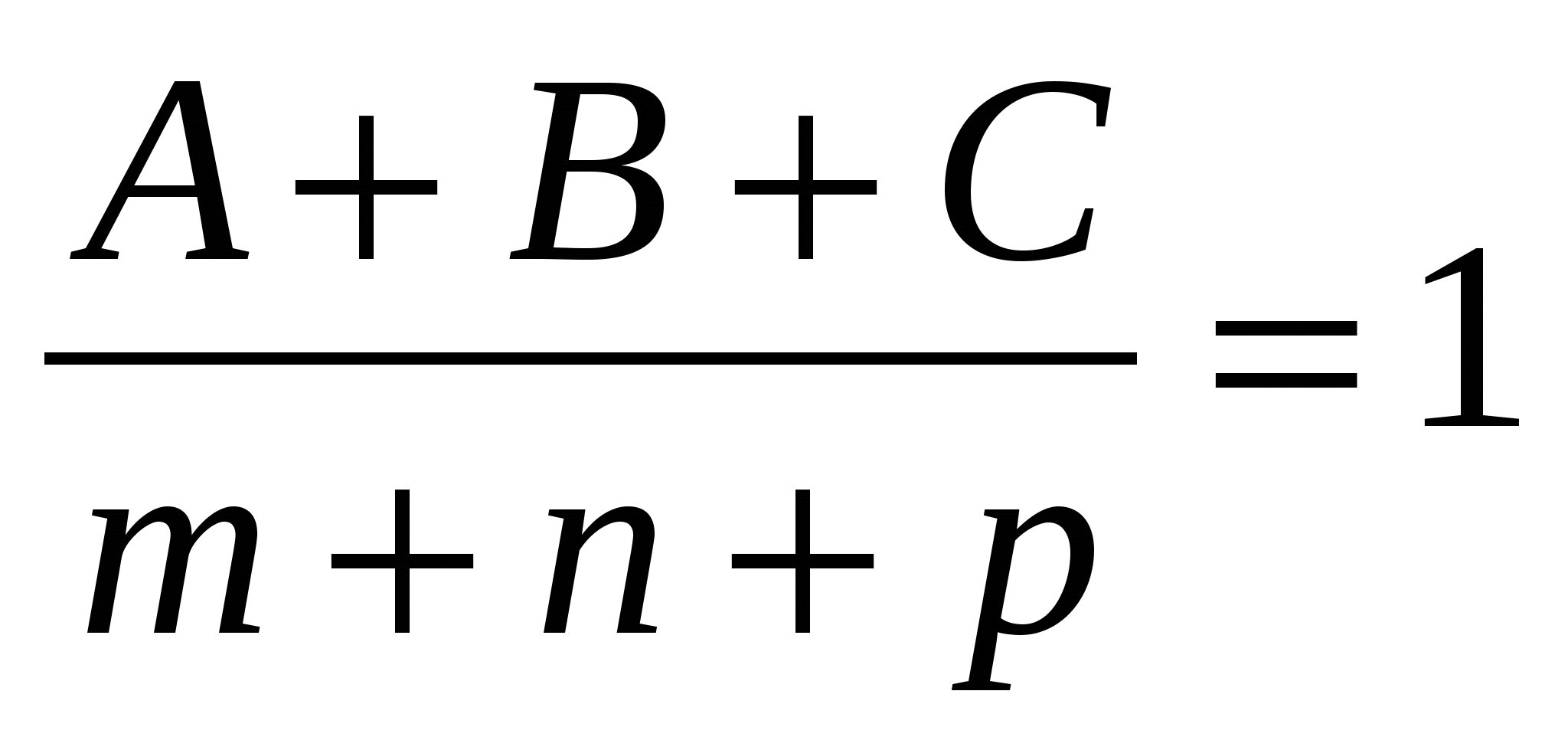
3. 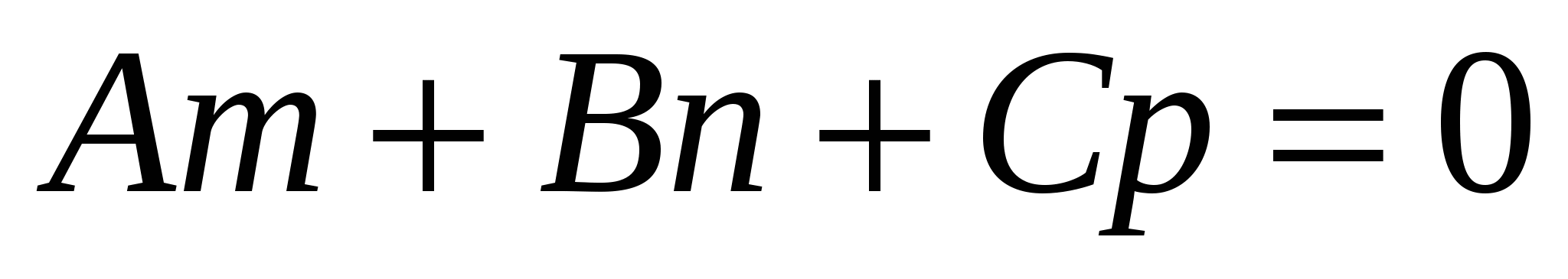
4. 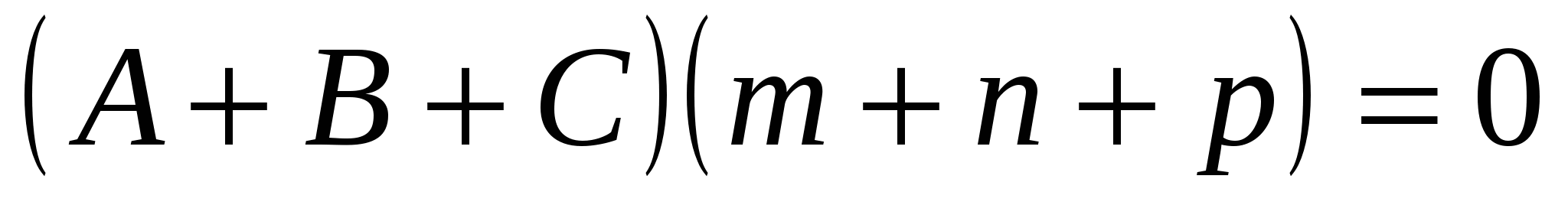
|
|
уравнение пучка плоскостей, проходящего через линию пересечения двух плоскостей в пространстве 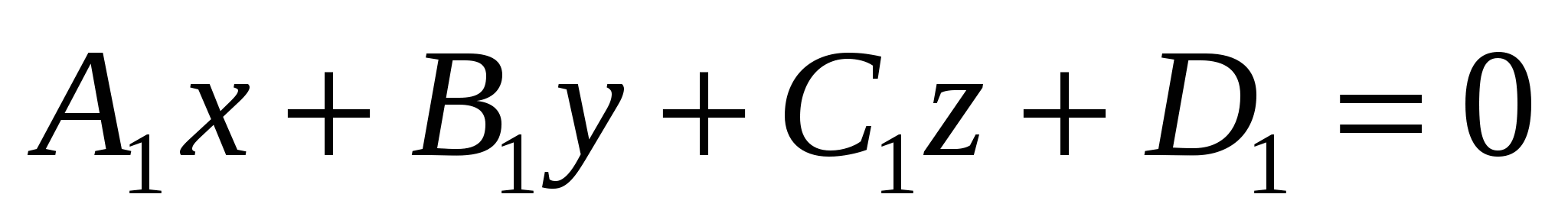 и и 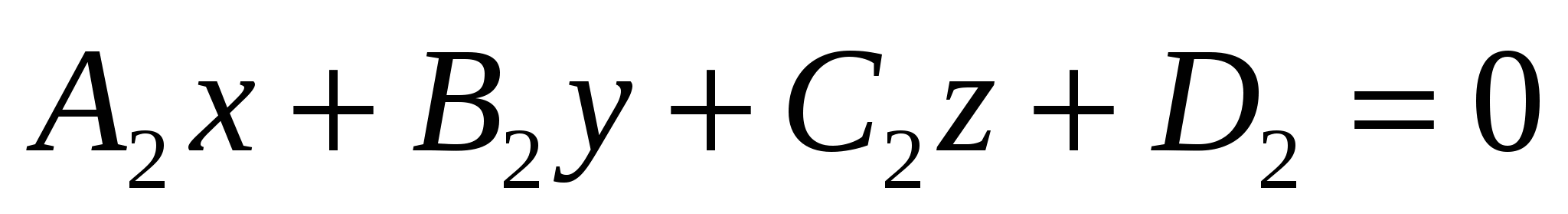 , имеет вид , имеет вид
|
1. 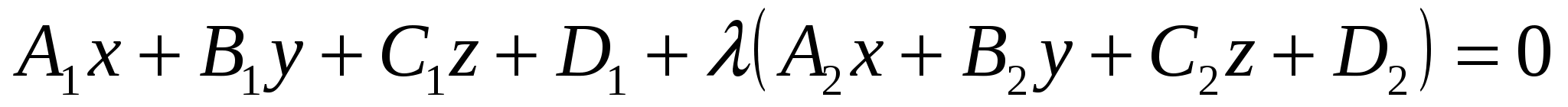
2.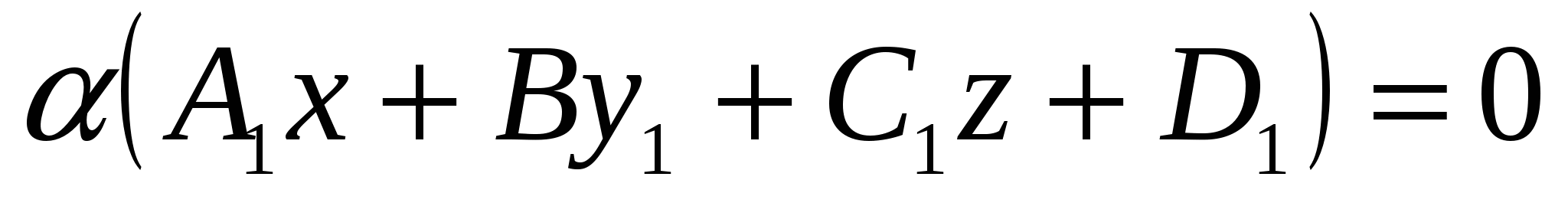
3.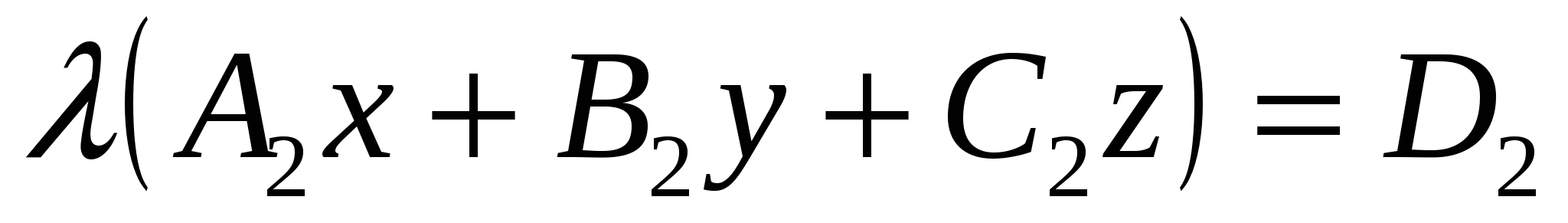
4.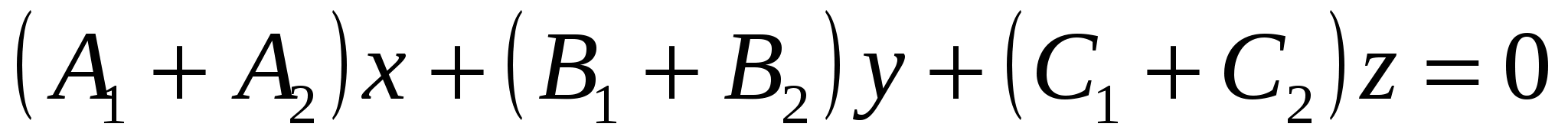
|
|
Какая из заданных плоскостей находится на расстоянии трех единиц от начала координат:
|
1. 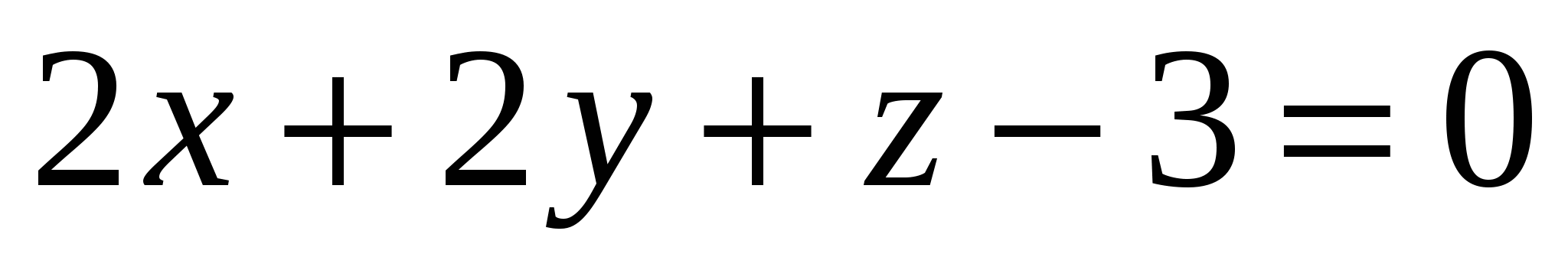 2. 2. 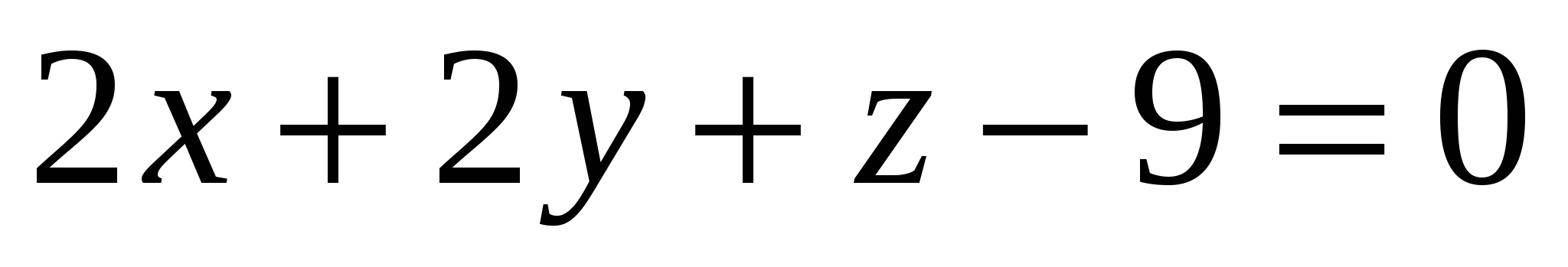
3. 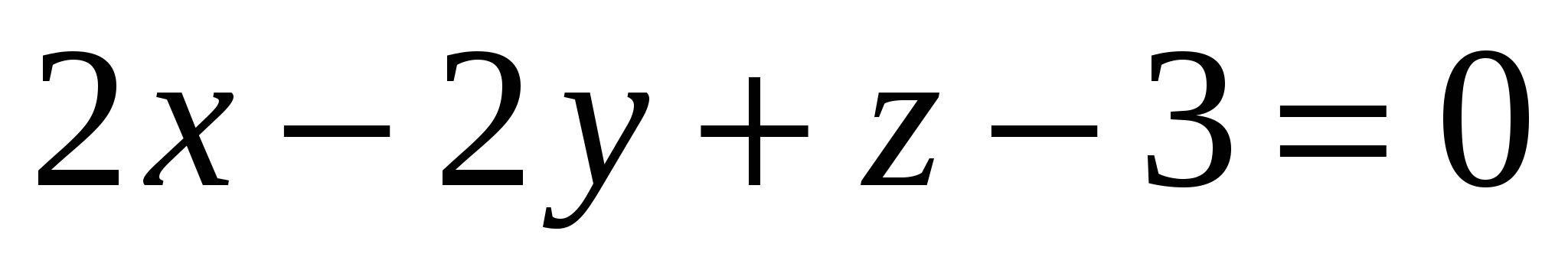 4. 4. 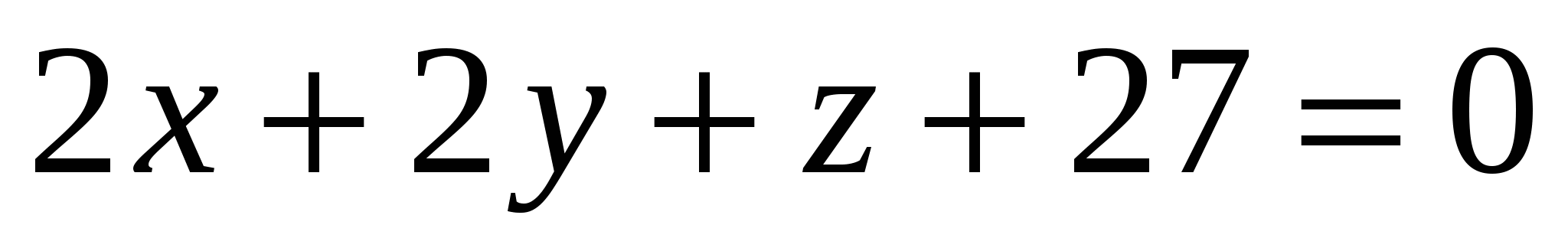
|
|
Какое из уравнений задает плоскость, проходящую через начало координат?
|
1. 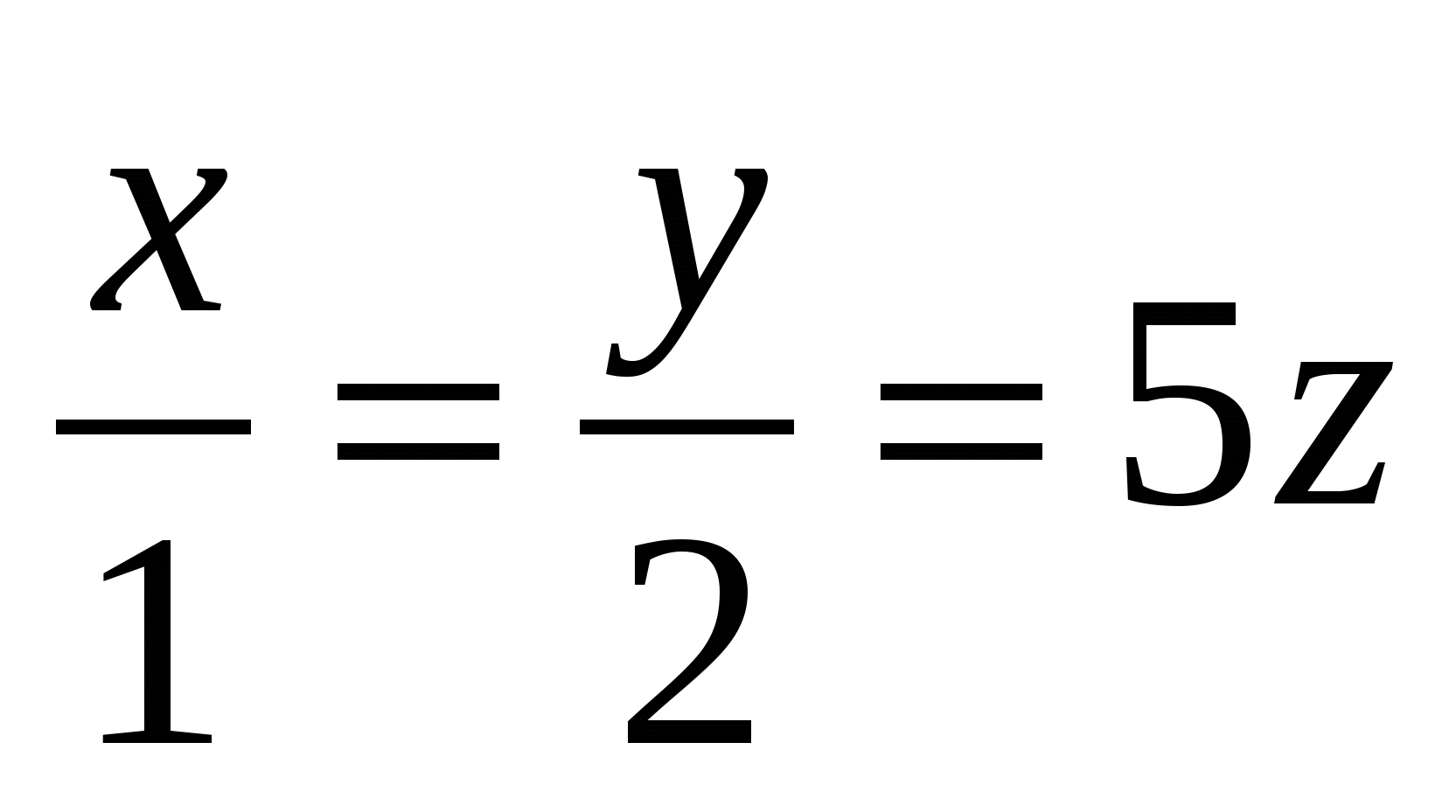 2. 2. 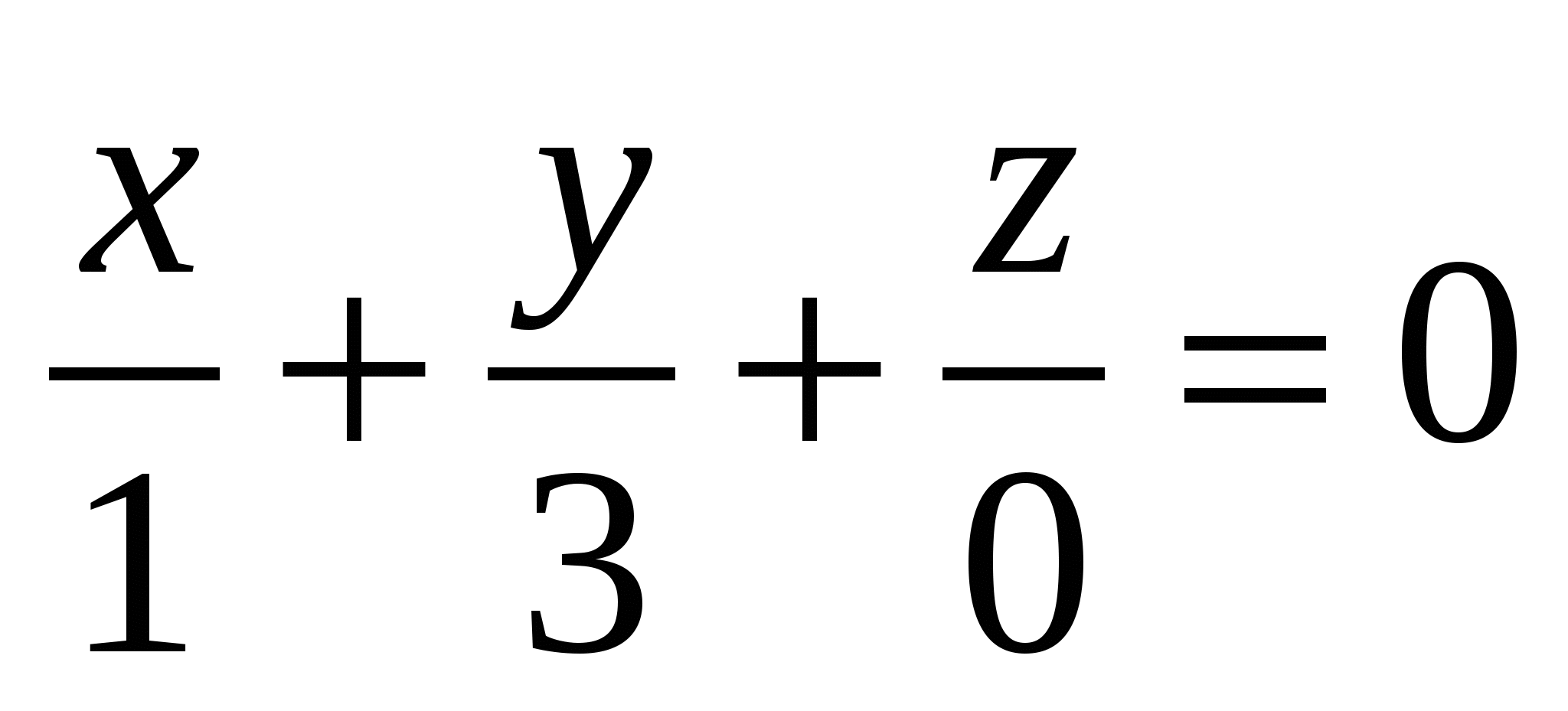
3. 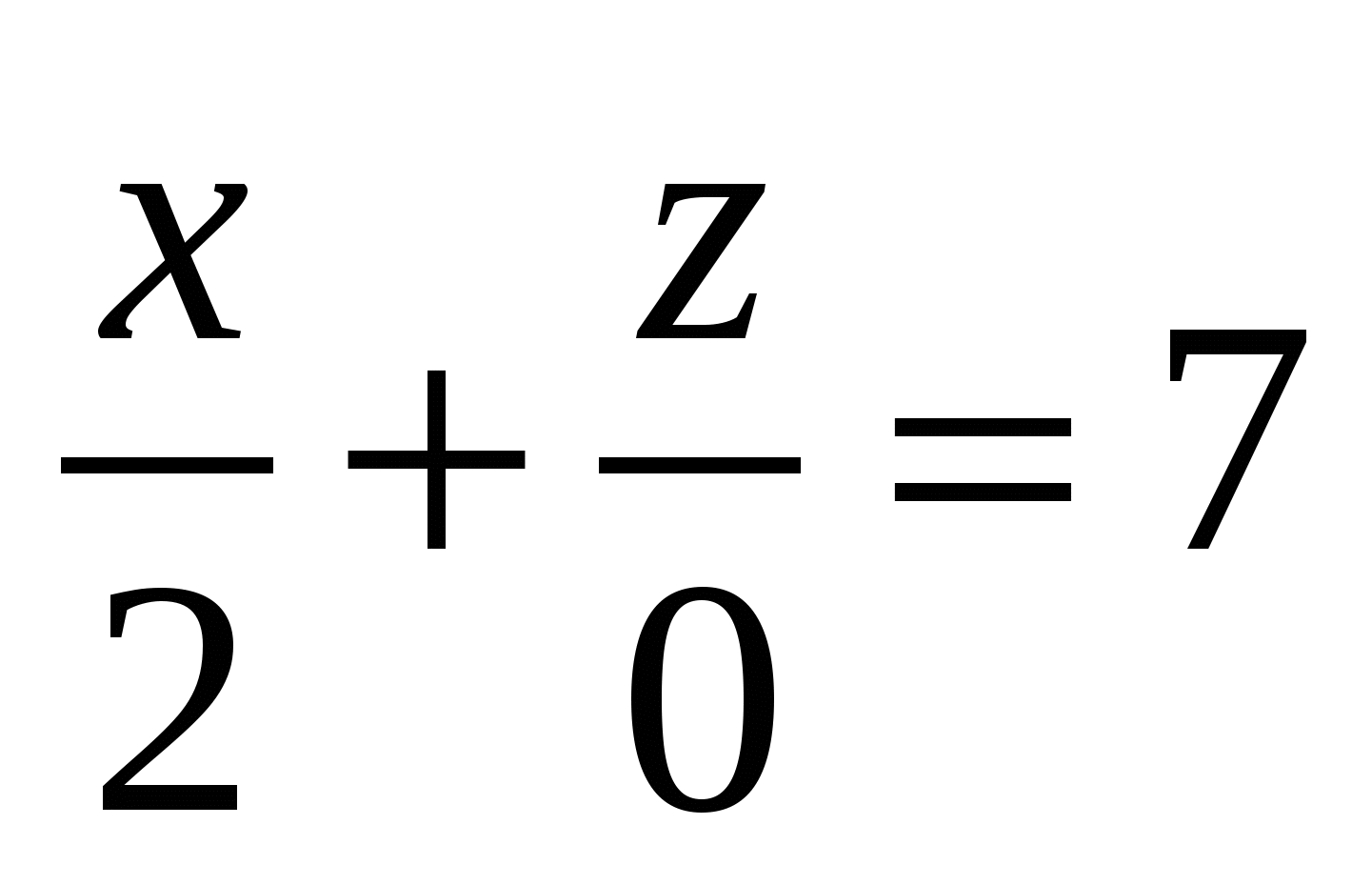 4. 4. 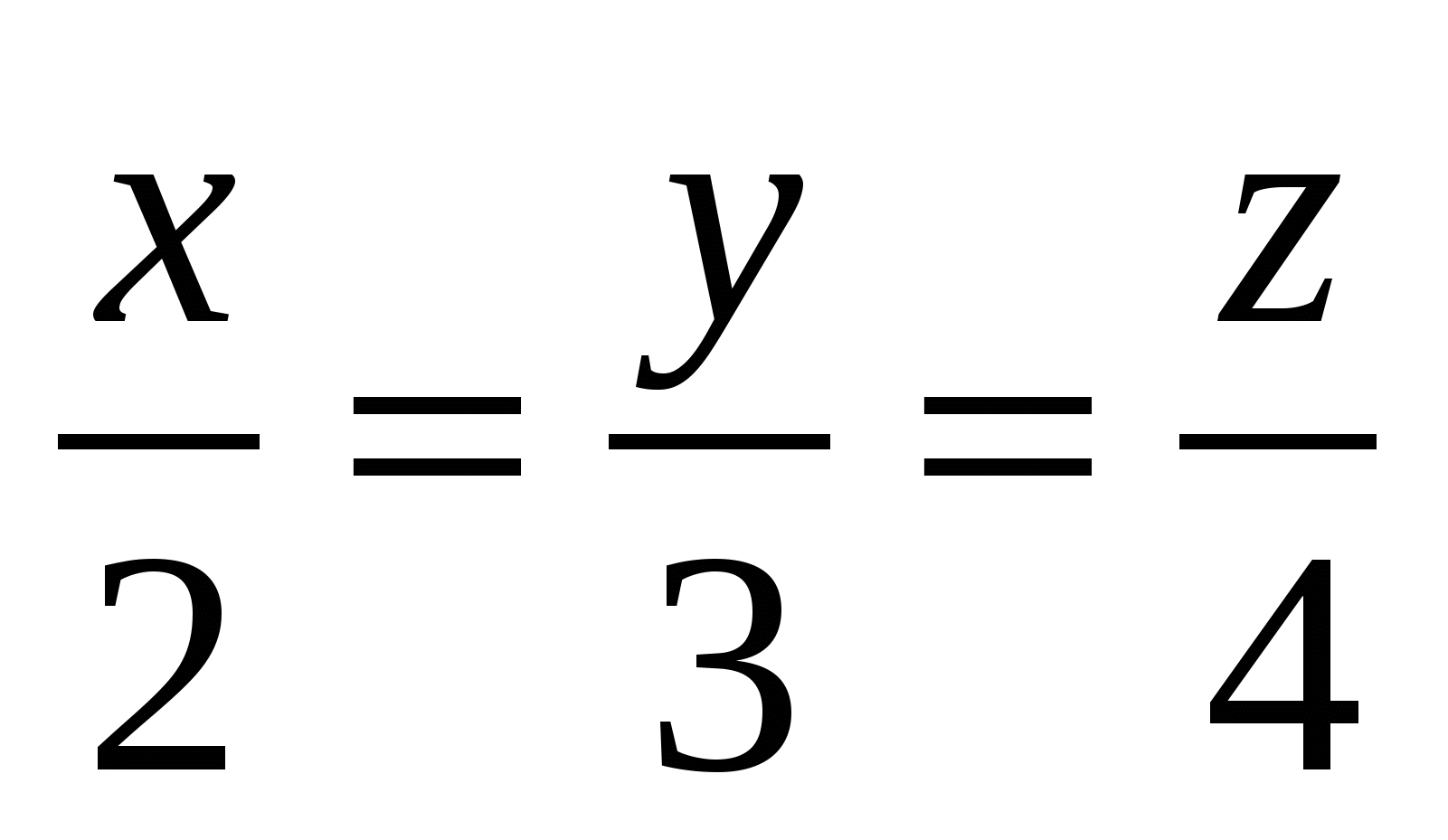
|
|
Укажите уравнения прямой, проходящей через начало координат
|
1.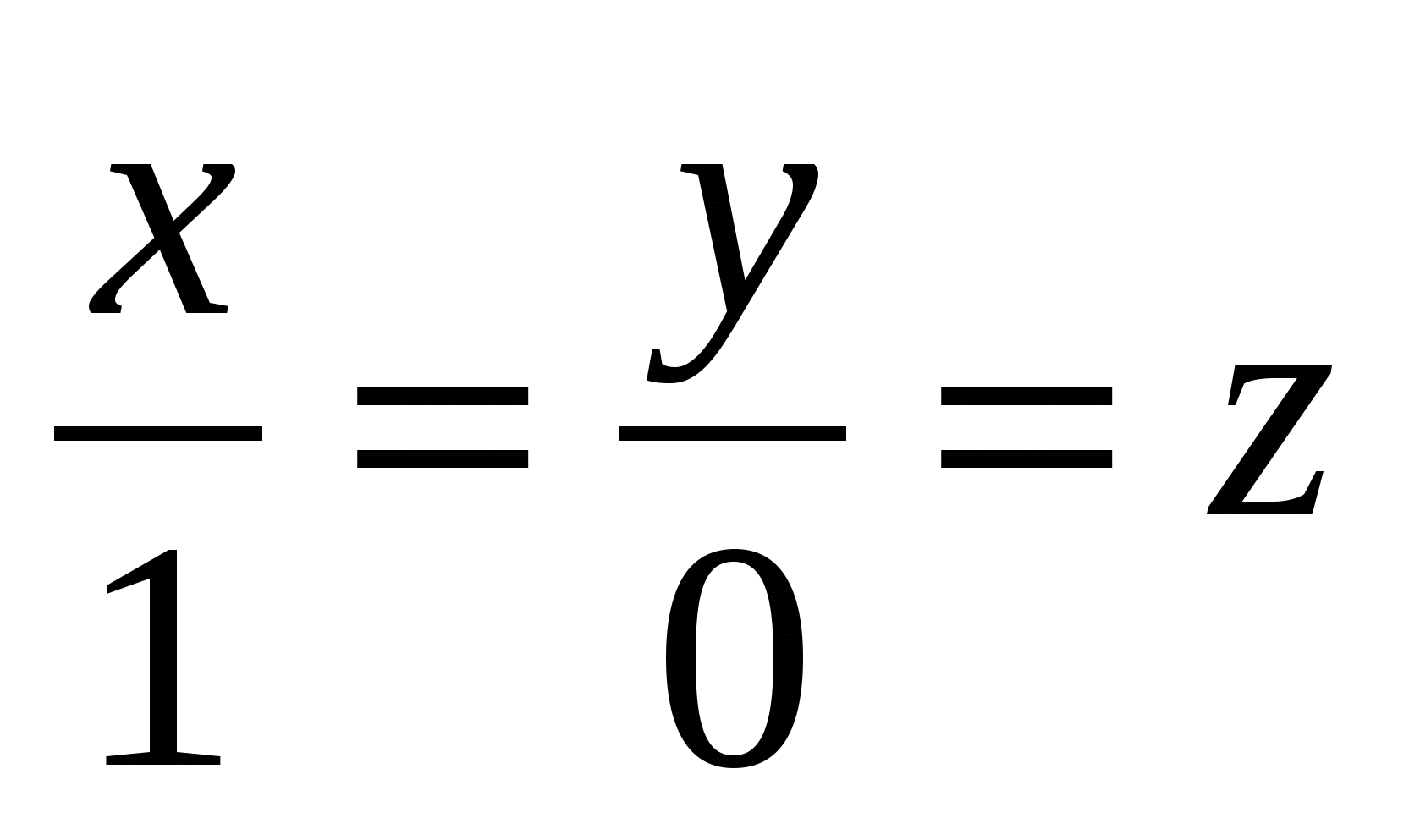
2.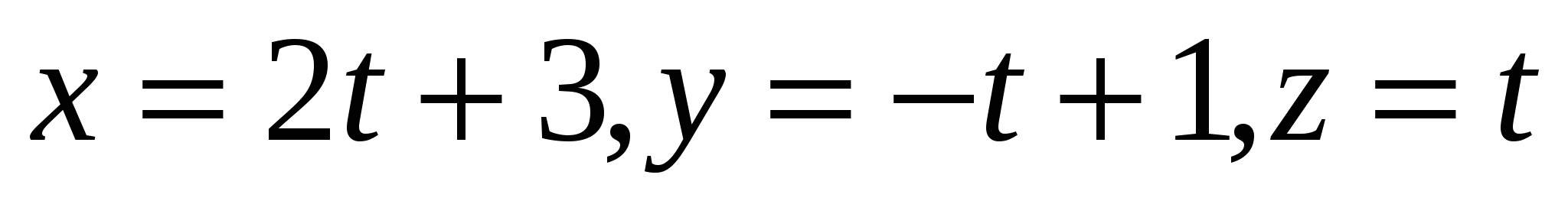
3.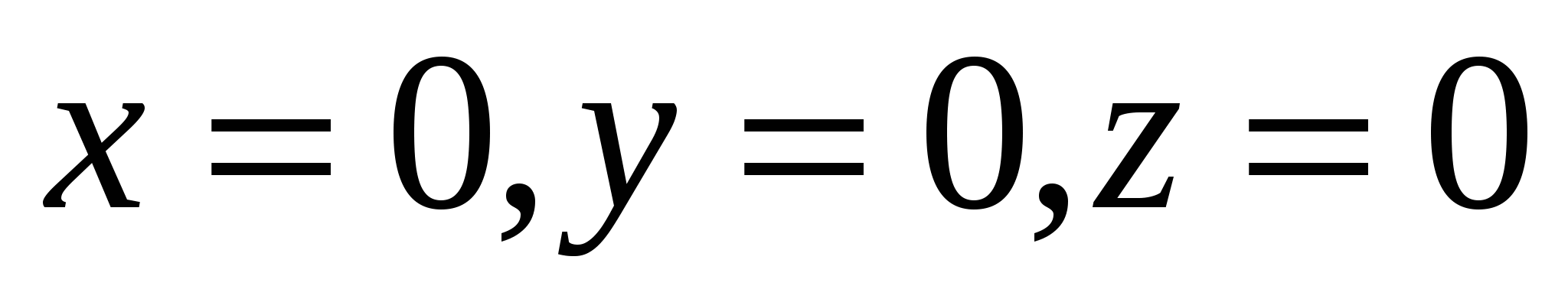
4. 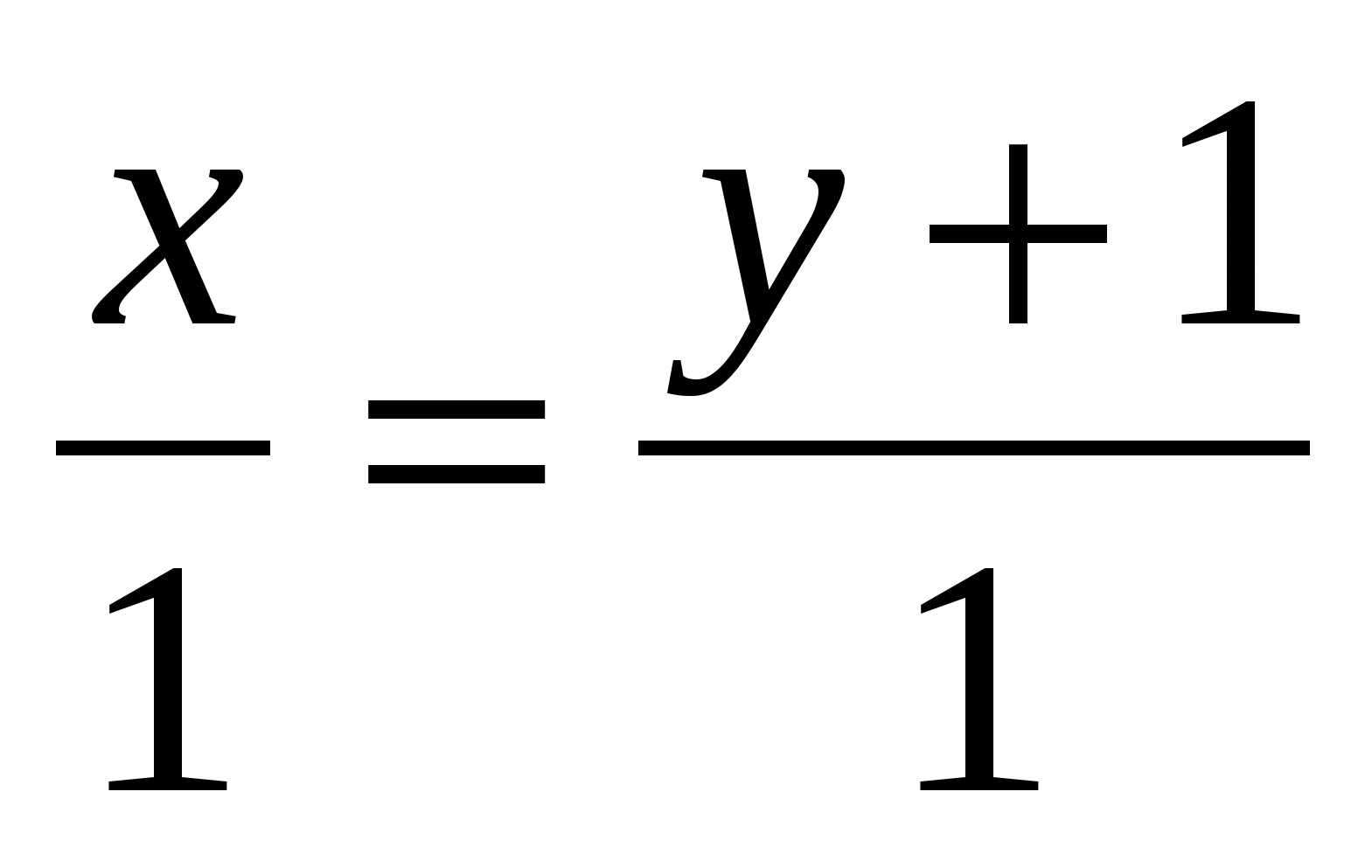
|
|
Канонические уравнения прямой, параллельной оси Ох, имеют вид
|
1. 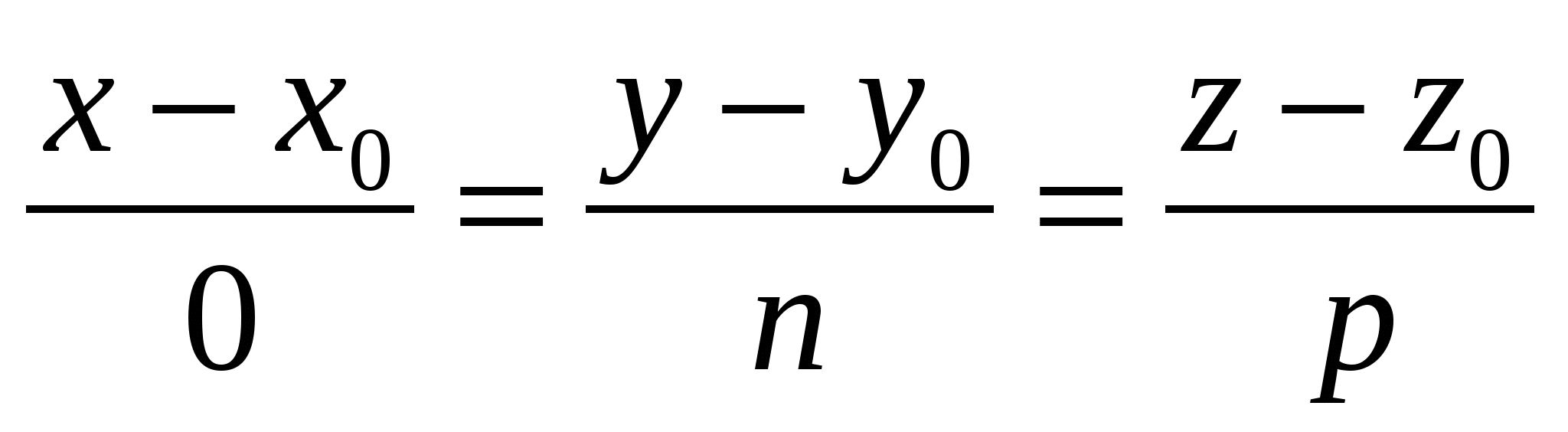
2. 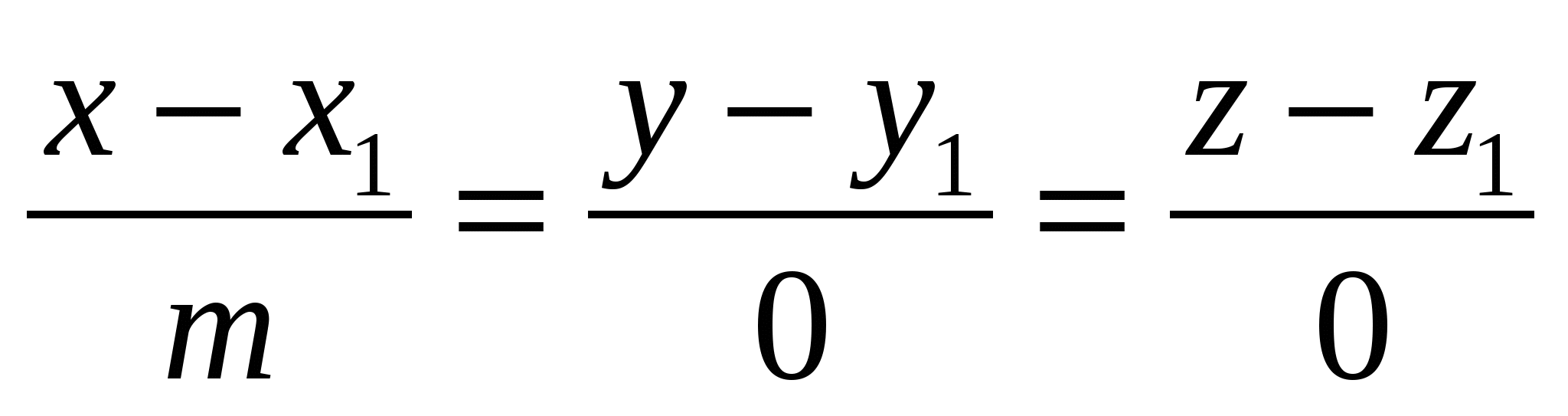
3. 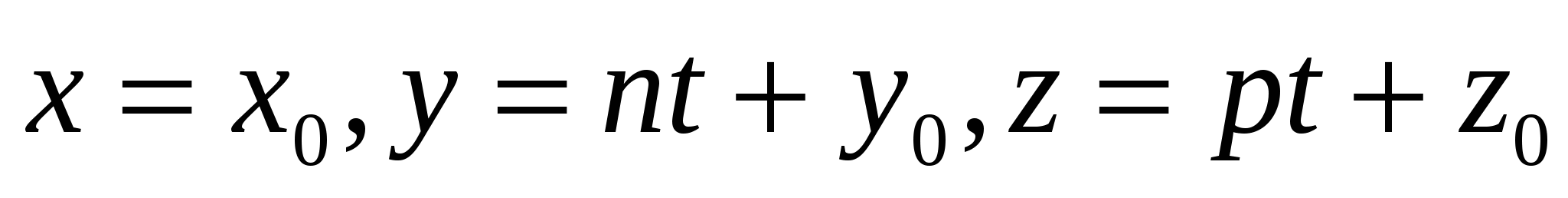
4. 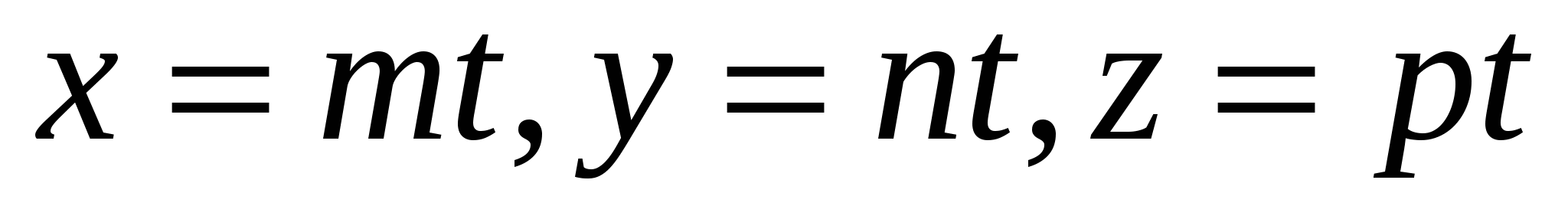
|
|
Угол между прямой между прямой 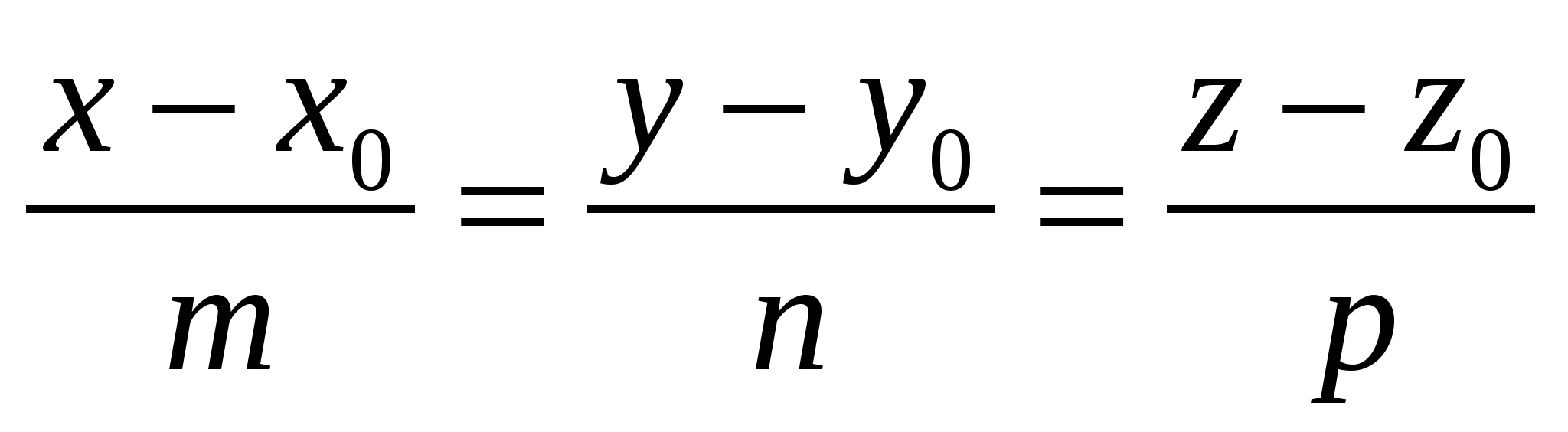 и плоскостью и плоскостью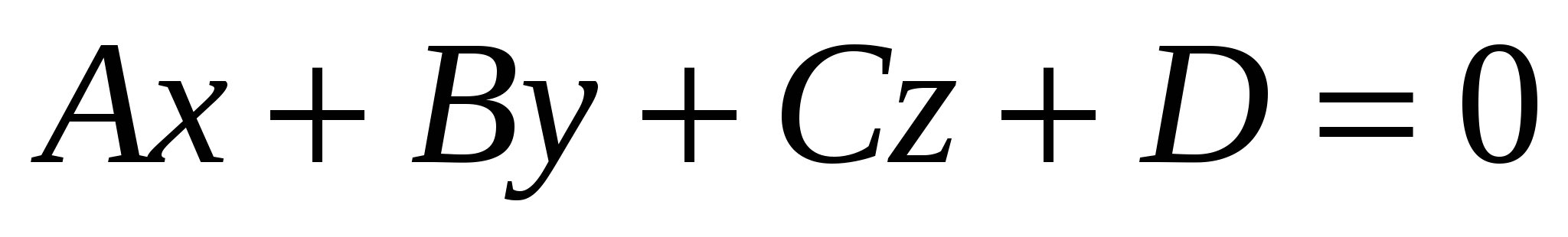 определяется с помощью формулы определяется с помощью формулы
|
1.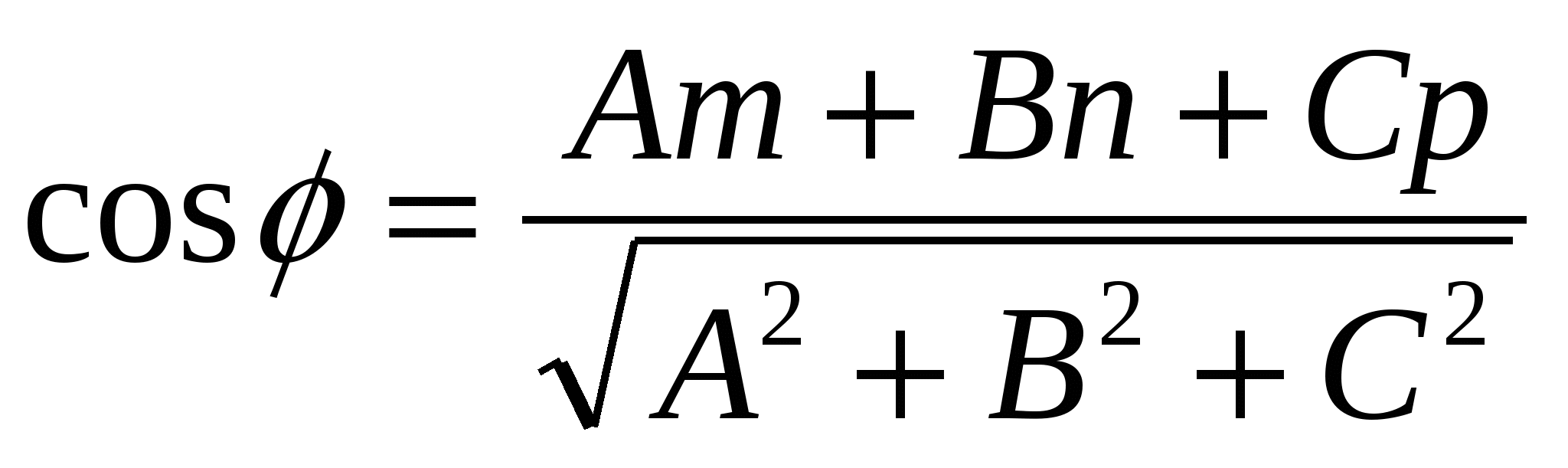
2. 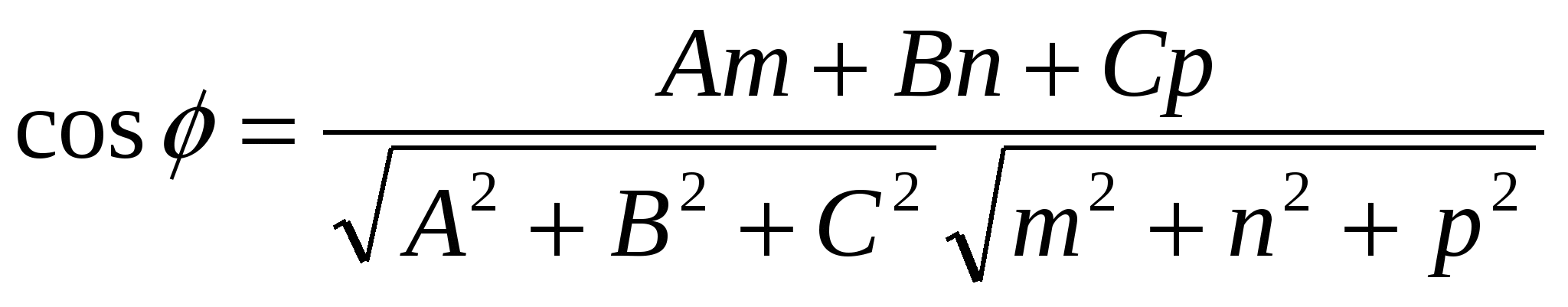
3. 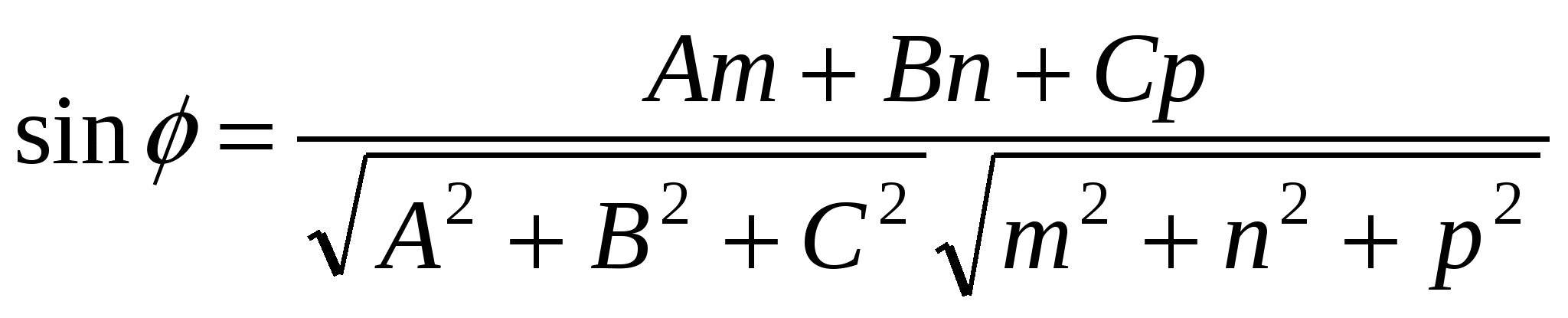
4. 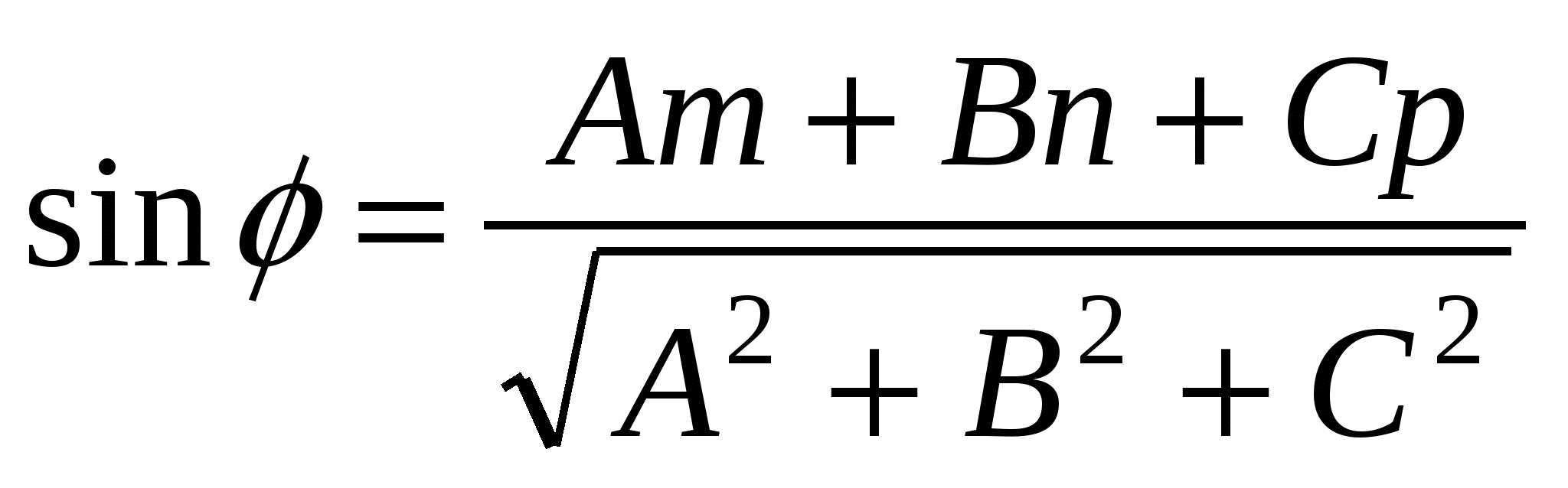
|
|
Какие из следующих уравнений задают ось ординат?
|
1. 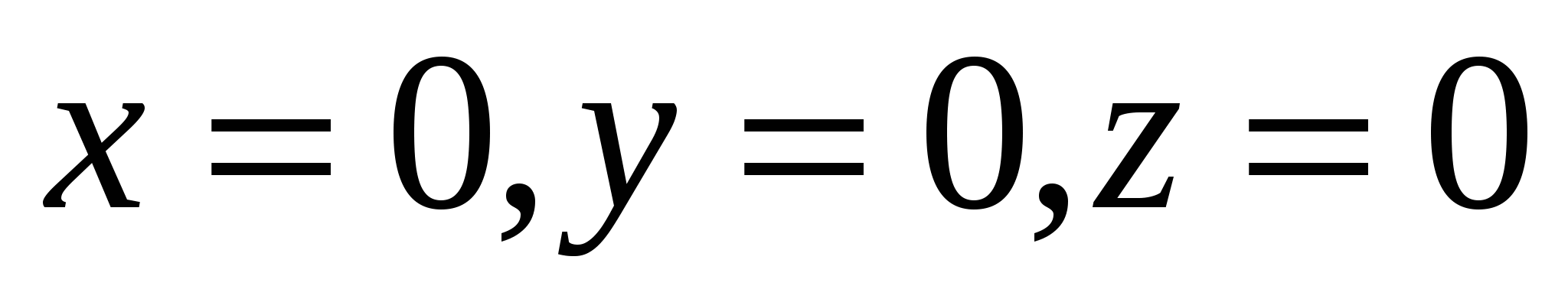
2. 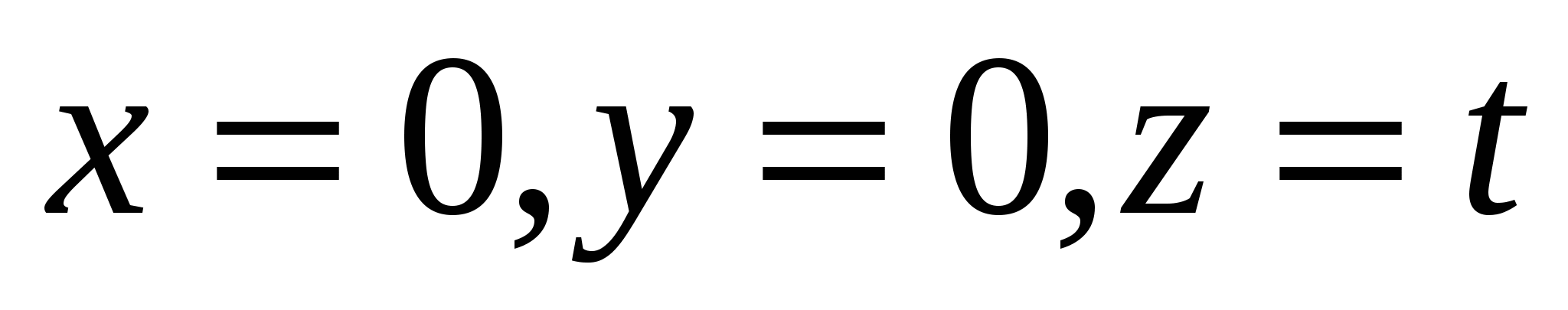
3. 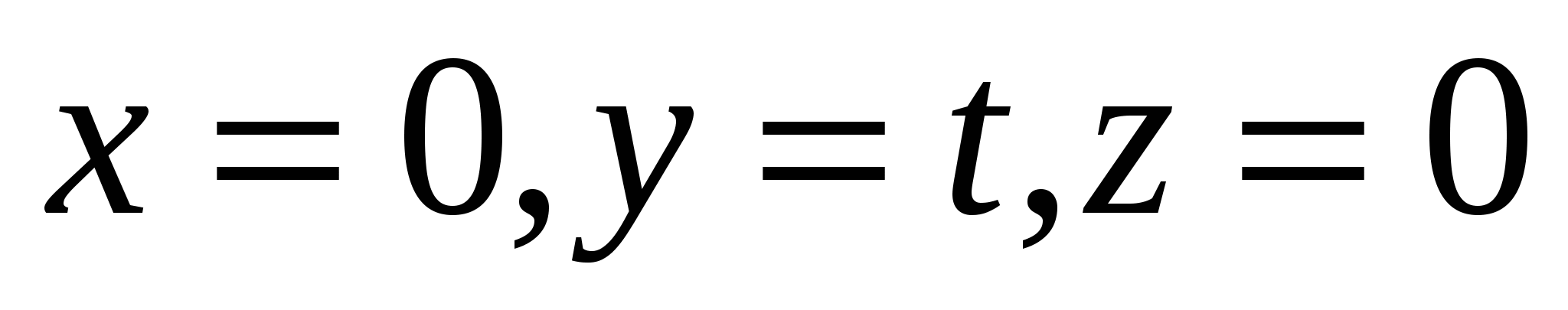
4. 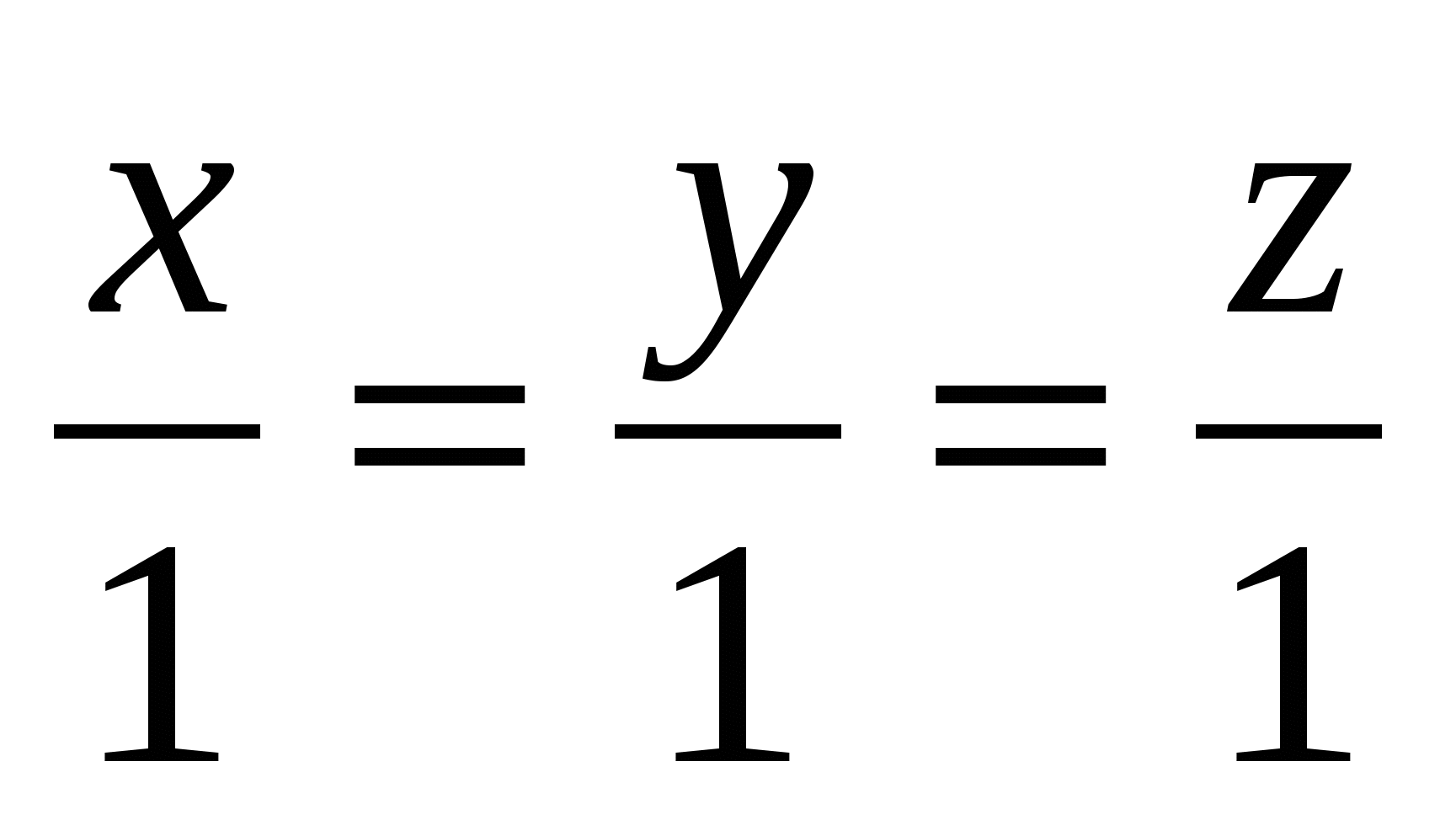
|
|
Какая из заданных прямых перпендикулярна прямой 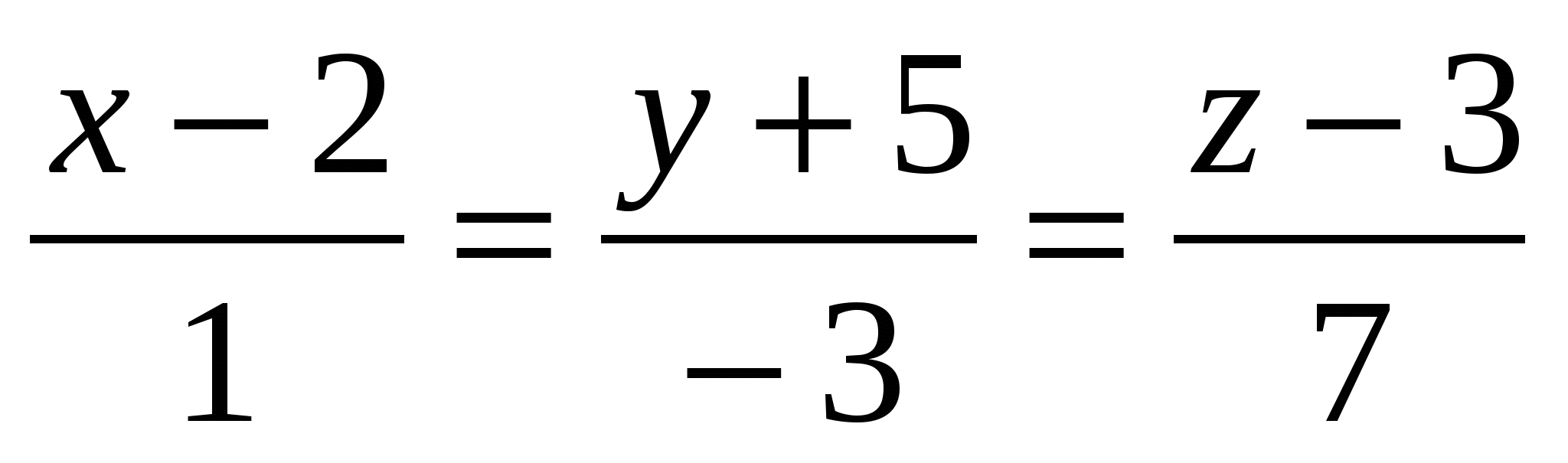
|
1. 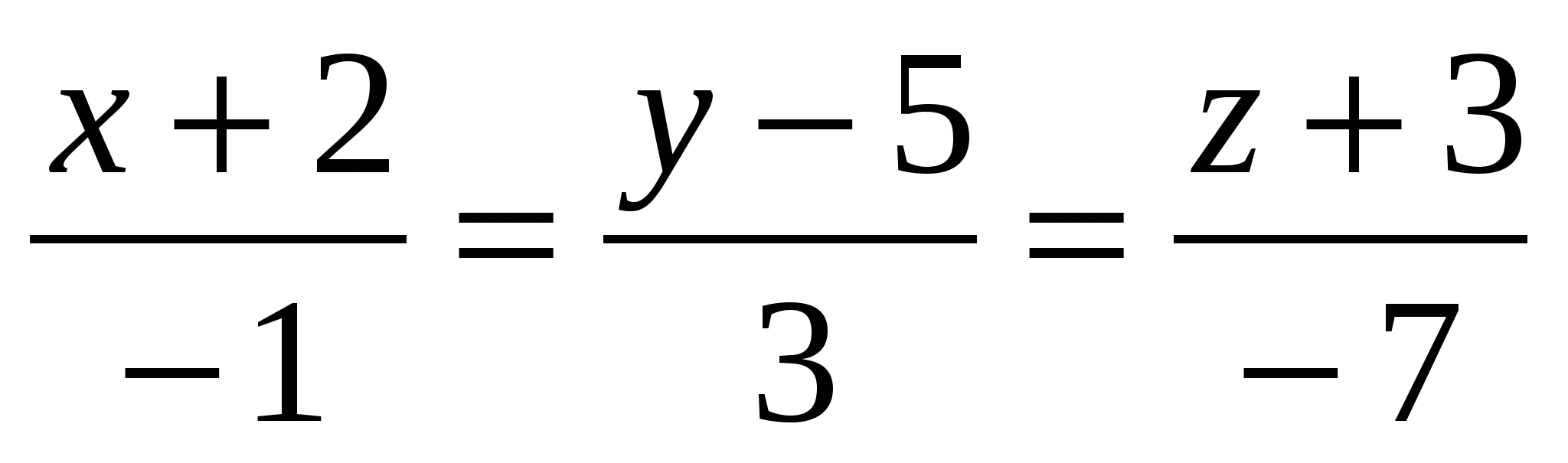
2. 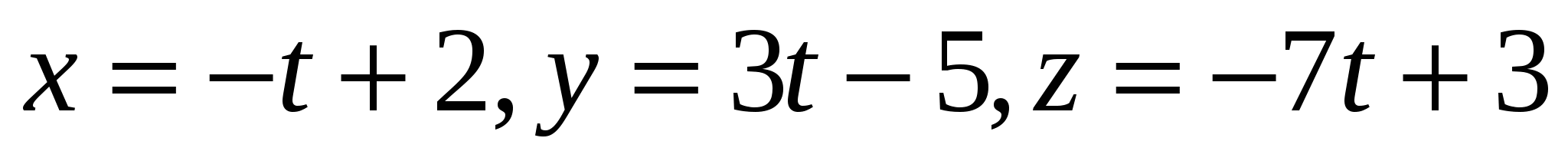
3. 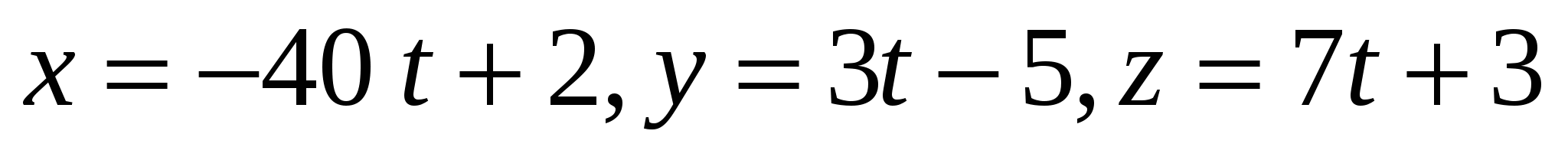
4. 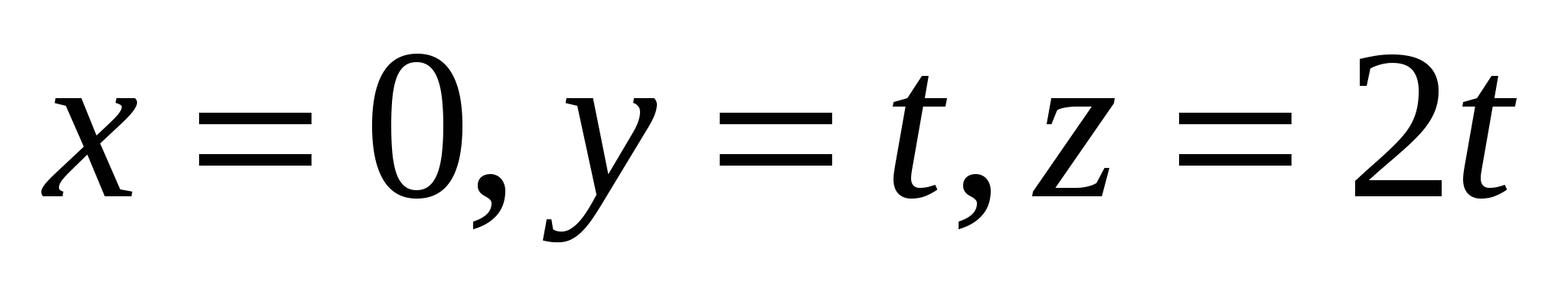
|
|
Угол между плоскостями 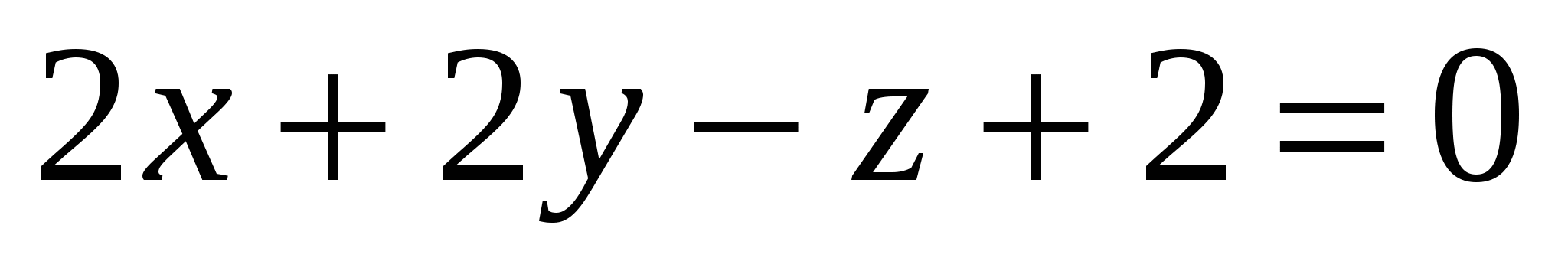 и и
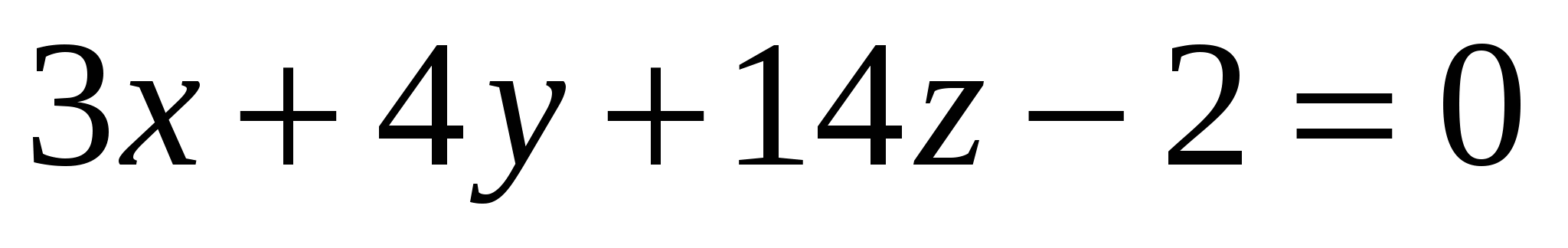 равен равен
|
1. 0
2. 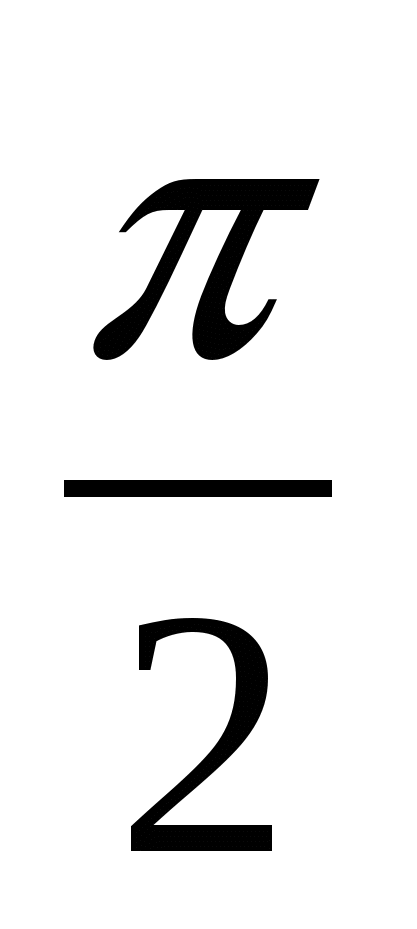
3. 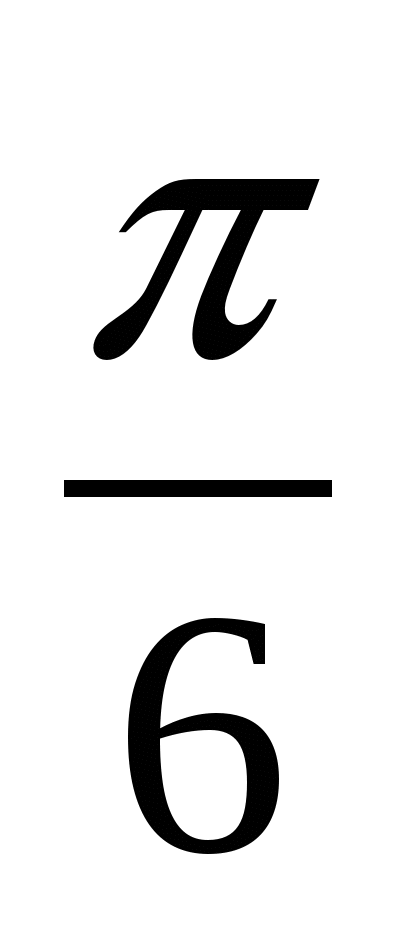
4. 
|
|
Какое из уравнений задает плоскость, параллельную оси Оу :
|
1. x + y z = 0 2. x z = 5
3. x + y z = 2 4. x + y = 6
|
|
Какое из уравнений задает плоскость, параллельную оси Оz:
|
1. 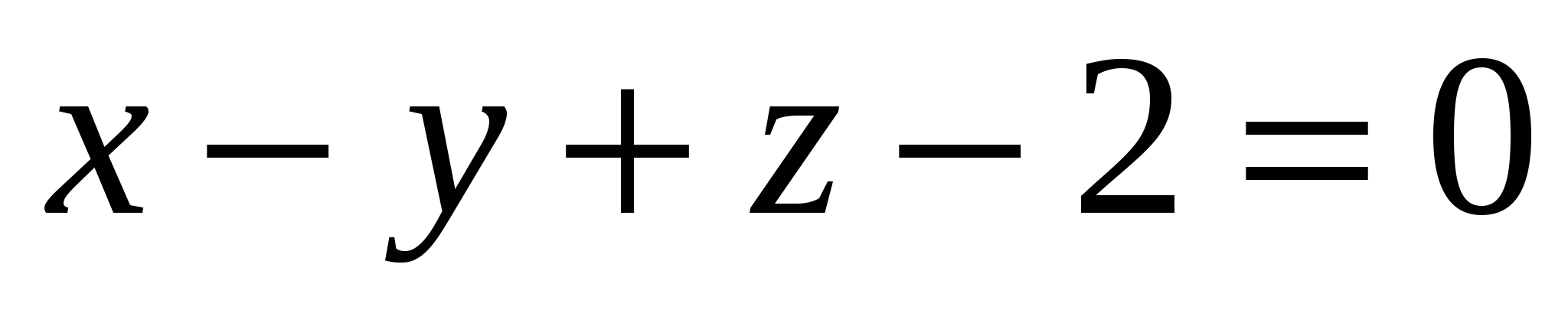
2. 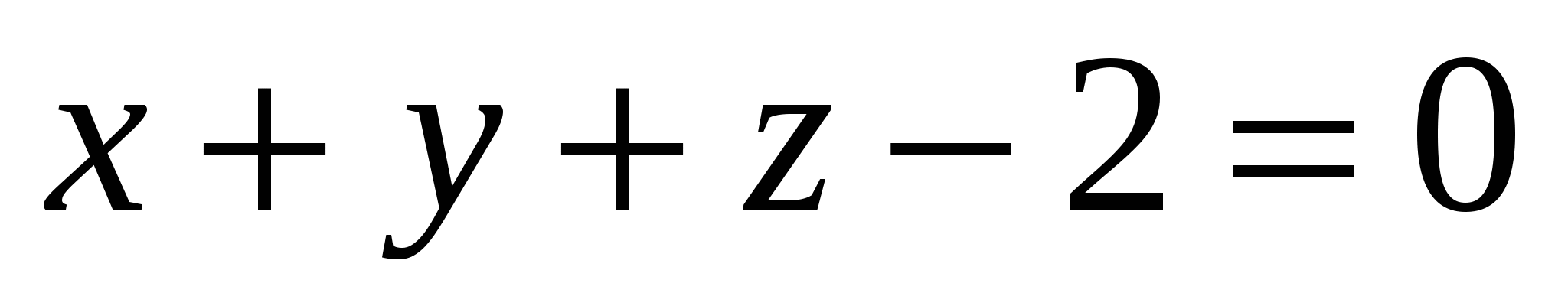
3. 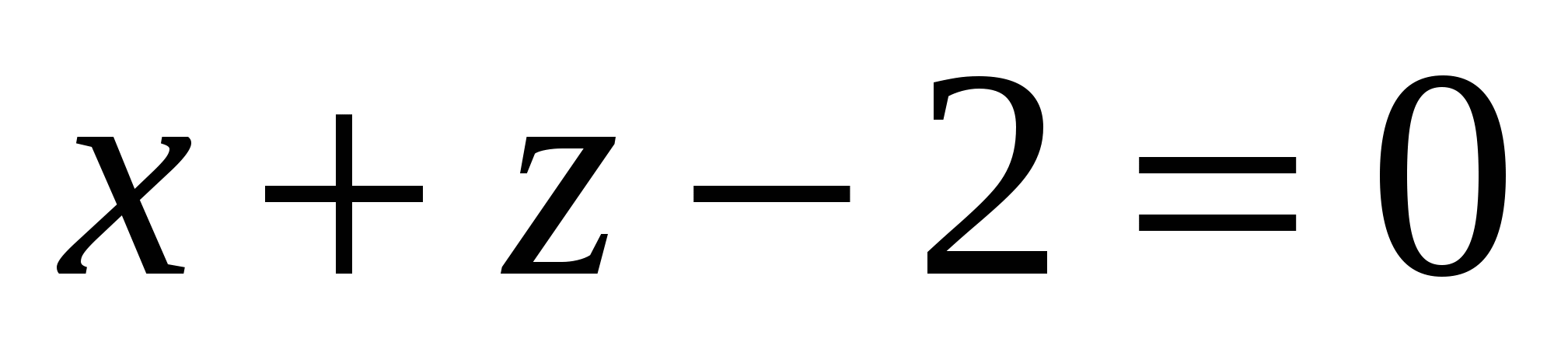
4. Правильного ответа в пп. 13 нет
|
|
Дано общее уравнение плоскости
Ax + By + Cz + D = 0.
Если в нем коэффициенты
A = 0, B = 0, C ≠ 0 и D ≠ 0,
то эта плоскость …
|
1. Параллельна плоскости Оxу
2. Параллельна плоскости Оyz
3. Параллельна плоскости Оxz
4. Параллельна оси Оz
|
|
Дано общее уравнение плоскости
Ax + By + Cz + D = 0.
Если в нем коэффициенты
A = 0, B ≠ 0, C = 0 и D ≠ 0,
то эта плоскость …
|
1. Параллельна плоскости Оxу
2. Параллельна плоскости Оyz
3. Параллельна плоскости Оxz
4. Параллельна оси Оу
|
|
Дано общее уравнение плоскости
Ax + By + Cz + D =0.
Если в нем коэффициенты
A ≠0, B = 0, C = 0 и D ≠ 0,
то эта плоскость …
|
1. Перпендикулярна оси Ох
2. Перпендикулярна оси Оy
3. Перпендикулярна оси Оz
4. Параллельна оси Ох
|
|
Дано общее уравнение плоскости
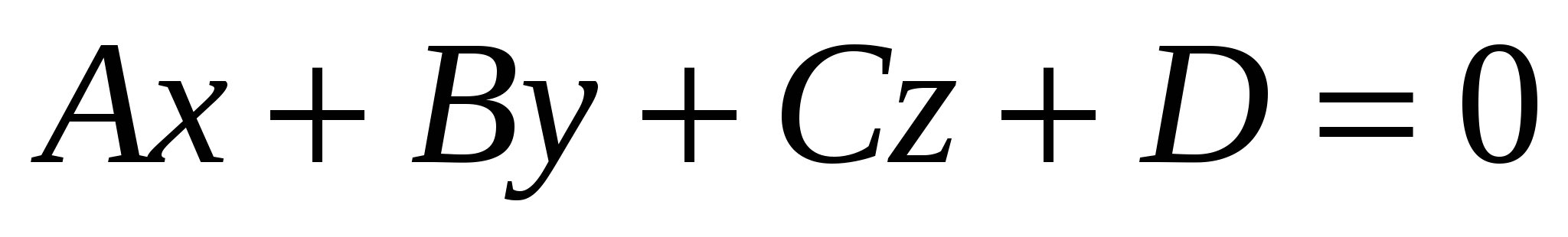 . .
Если в нем коэффициенты
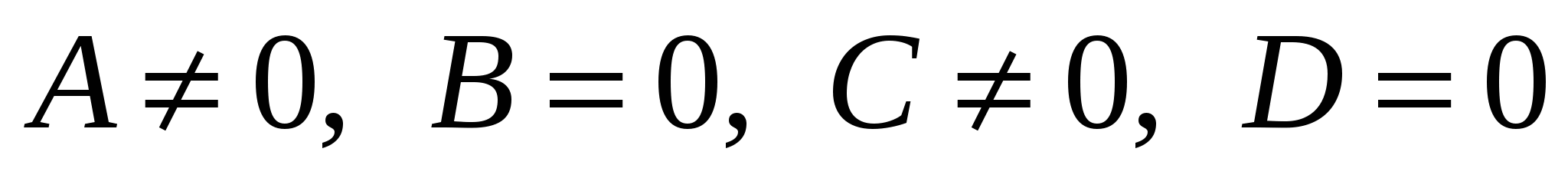 , ,
то эта плоскость …
|
1. Параллельна плоскости Оху
2. Перпендикулярна оси Оу
3. Содержит ось Оу
4. Правильного ответа в пп. 13 нет
|
|
Дано общее уравнение плоскости
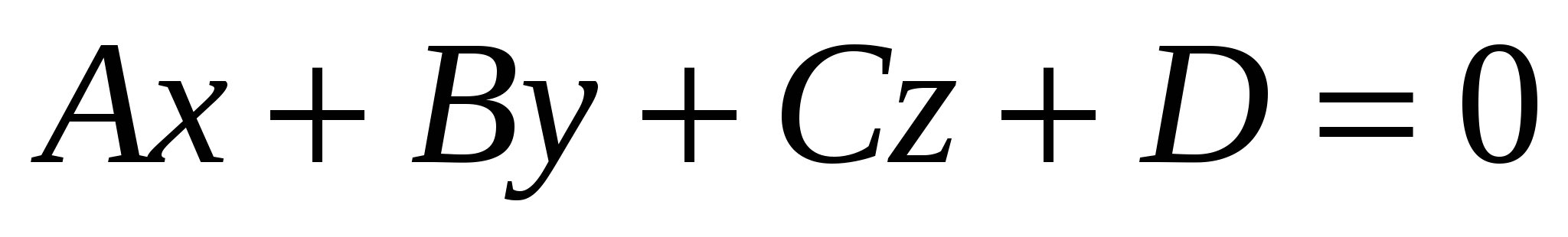 . .
Если в нем коэффициенты
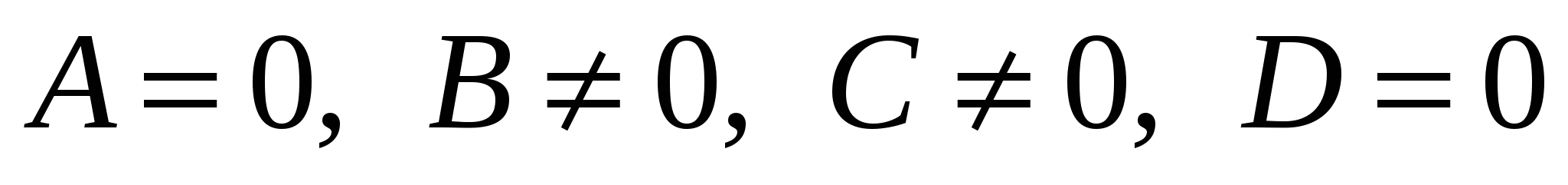 , ,
то эта плоскость …
|
1. Параллельна плоскости Оху
2. Параллельна плоскости Оуz
3. Параллельна плоскости Охz
4. Содержит ось Ох
|
|
Указать условие перпендикулярности двух плоскостей:
A1 x + B1 y + C1 z + D1=0
и
A2 x + B2 y + C2 z + D2=0:
|
1. A1 A2 + B1 B2 + C1 C2 + D1D2 = 0
2. A1 A2 + B1 B2 + C1 C2 = 0
3. 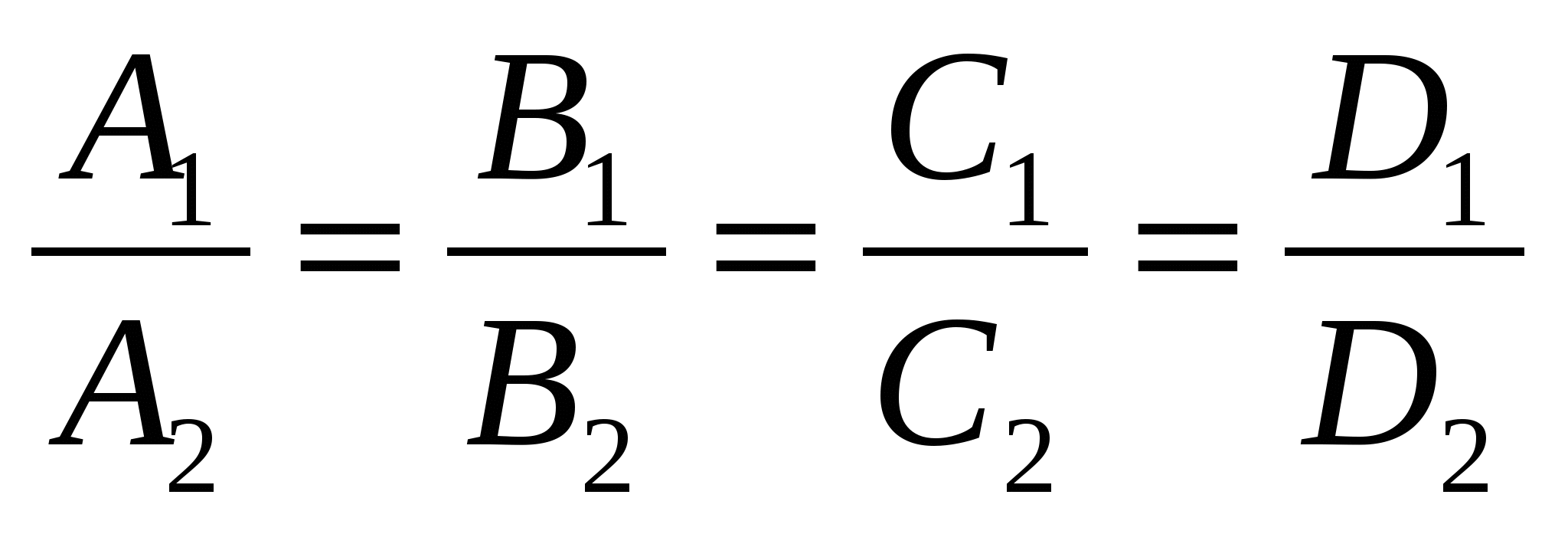
4. 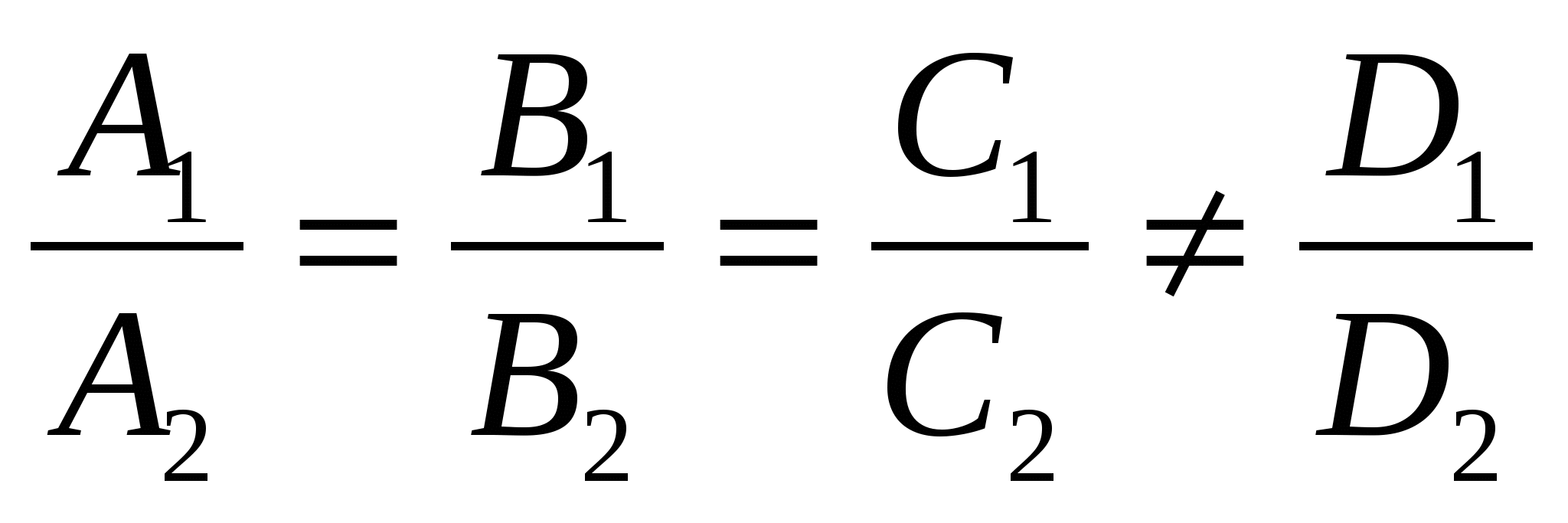
|
|
Укажите уравнения прямой, проходящей через начало координат:
|
1. x = y = z
2. x +1 = y 1 = z
3. x = y 5
4. x = 2t 1, y = 6, z = 8 3t
|
|
Какие из следующих уравнений задают ось ординат?
|
1. x = t, y = 0, z = 0 2. x = 0, y = 0, z = 0
3. x = 0, y = t, z = 0 4. x = t, y = t, z = t
|
|
Угол между прямыми
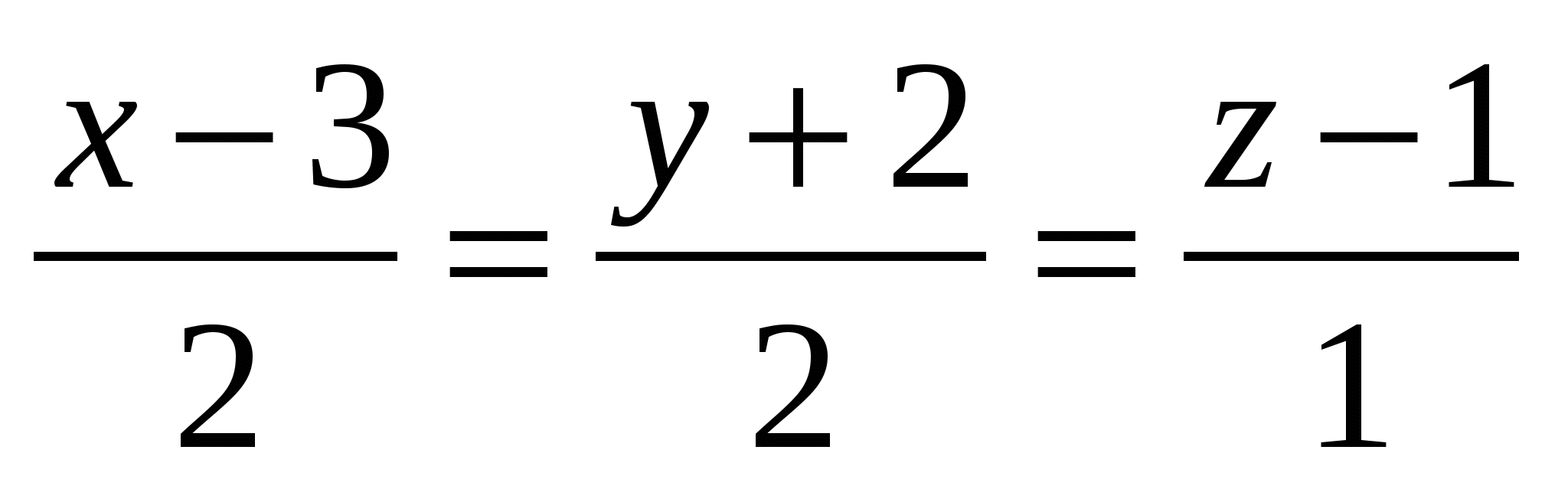 и и 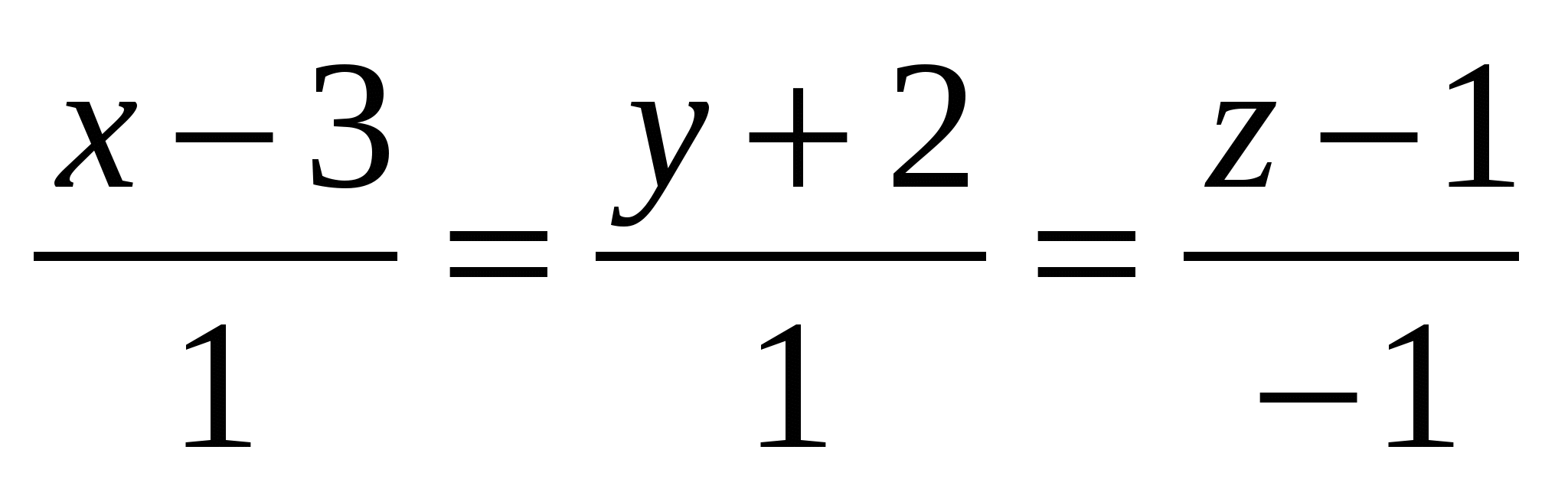
|
1. 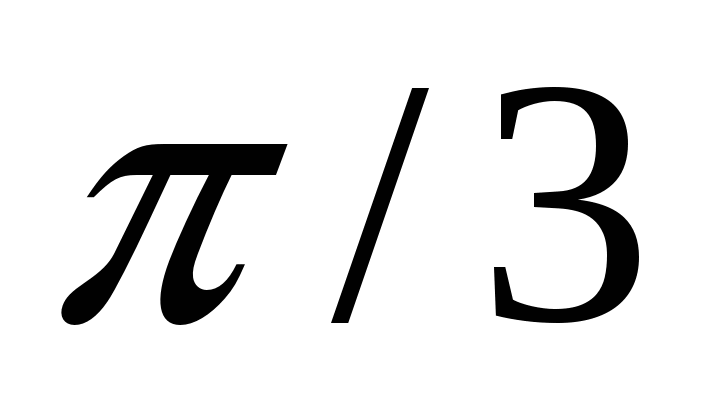
2. 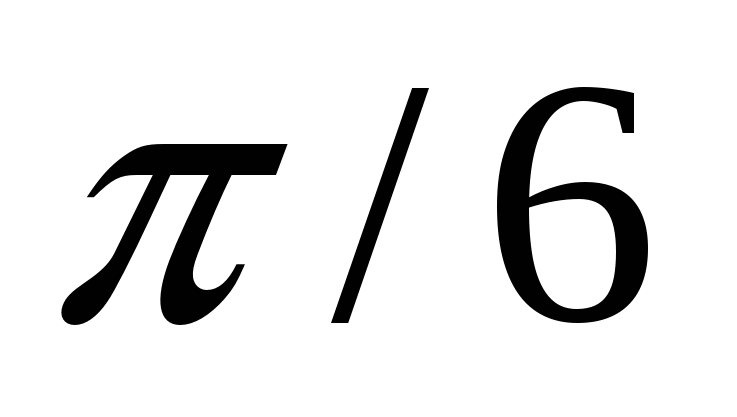
3 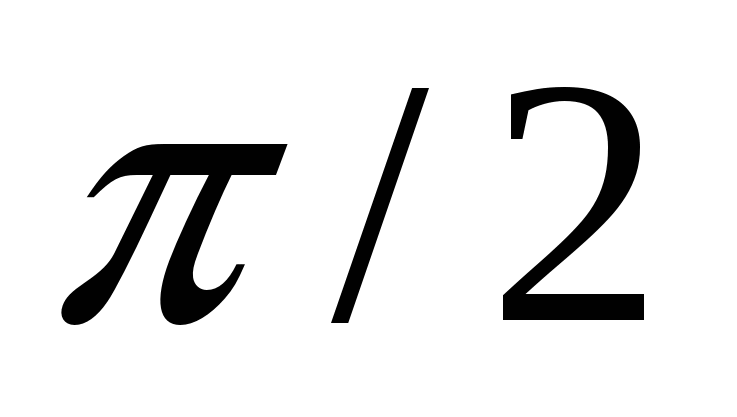
4. 0
|
|
В какой точке прямая
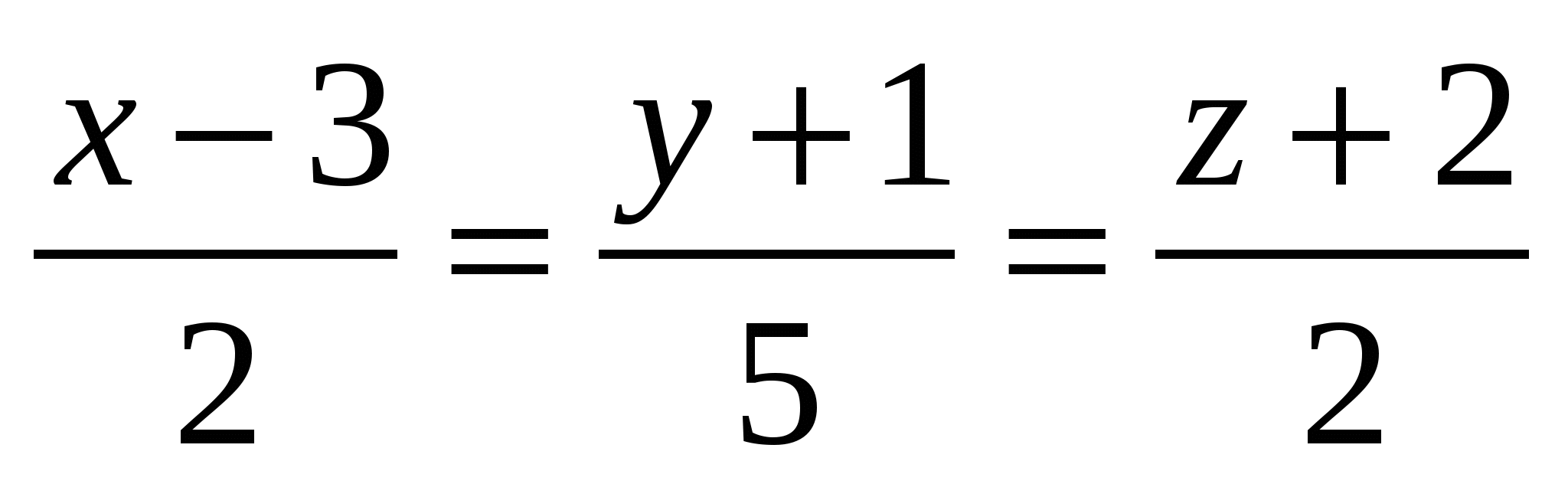
пересекает плоскость Охy:
|
1. (0; 0; – 2)
2. (-3; – 1; -2)
3. (5; 4; 0)
4. Эта прямая не пересекает плоскость Оху
|
|
Направляющие косинусы прямой
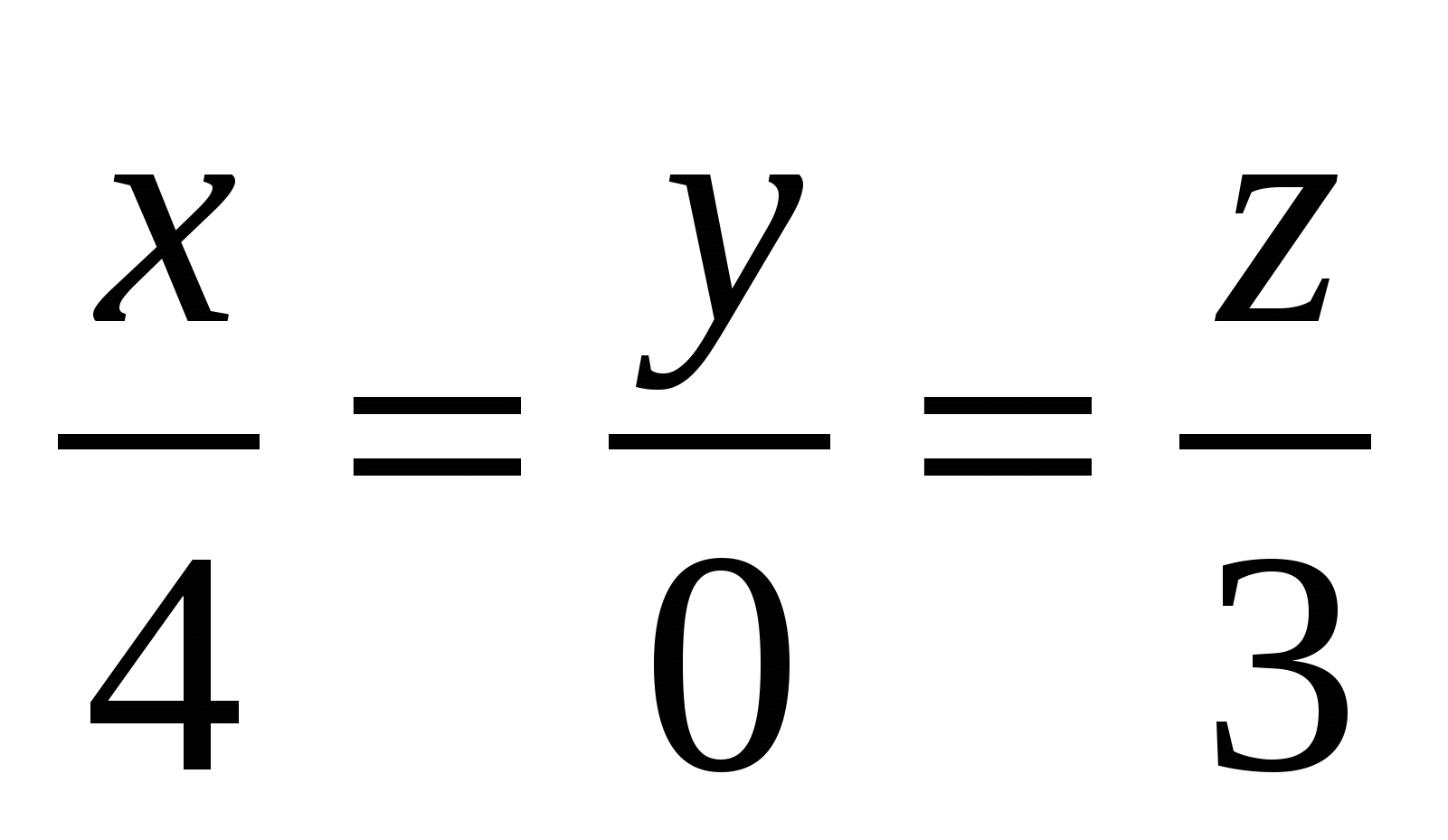 : :
|
1. 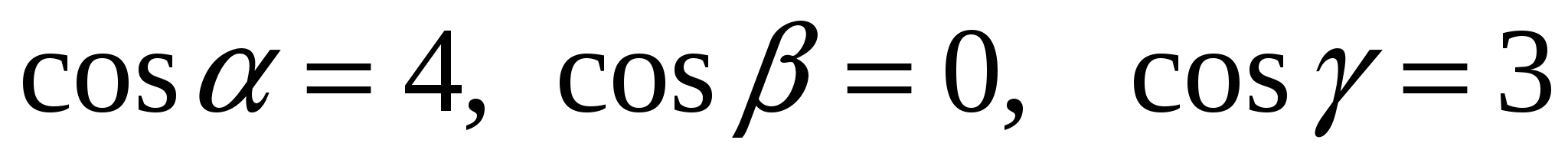
2. 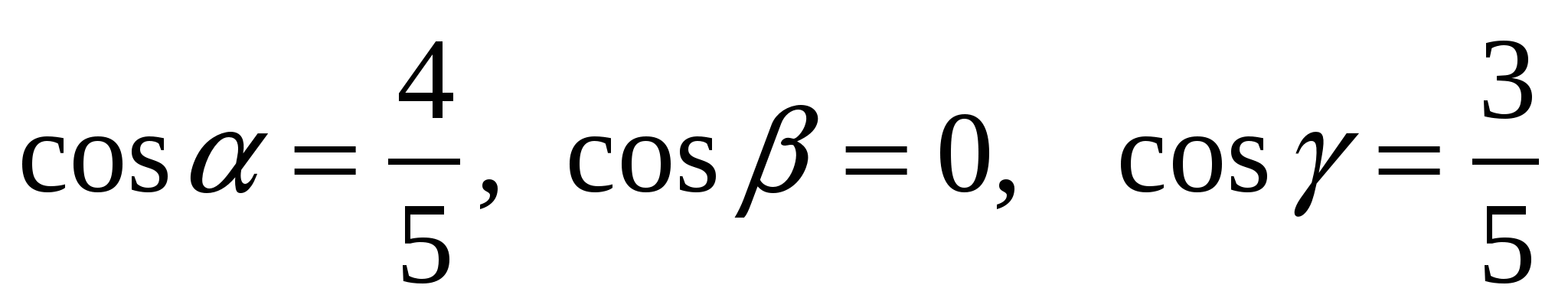
3. 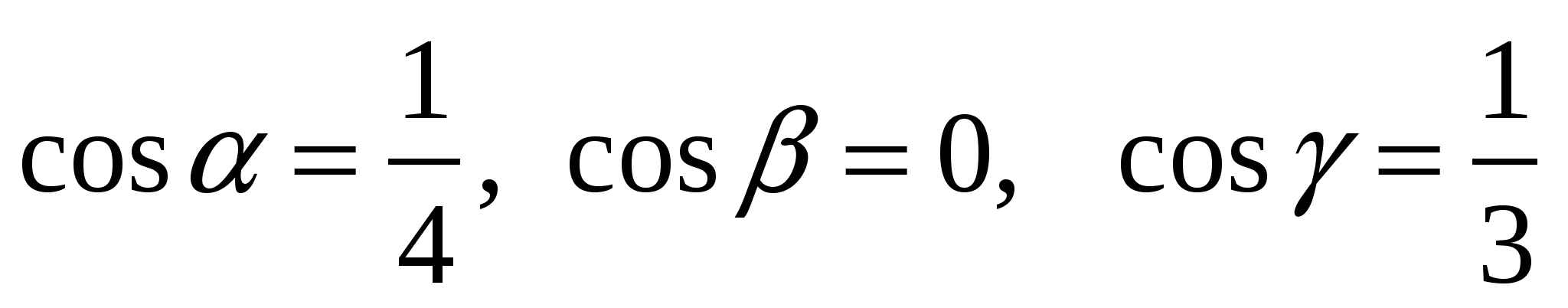
4. Правильного ответа в пп.1-3 нет
|
|
Уравнение 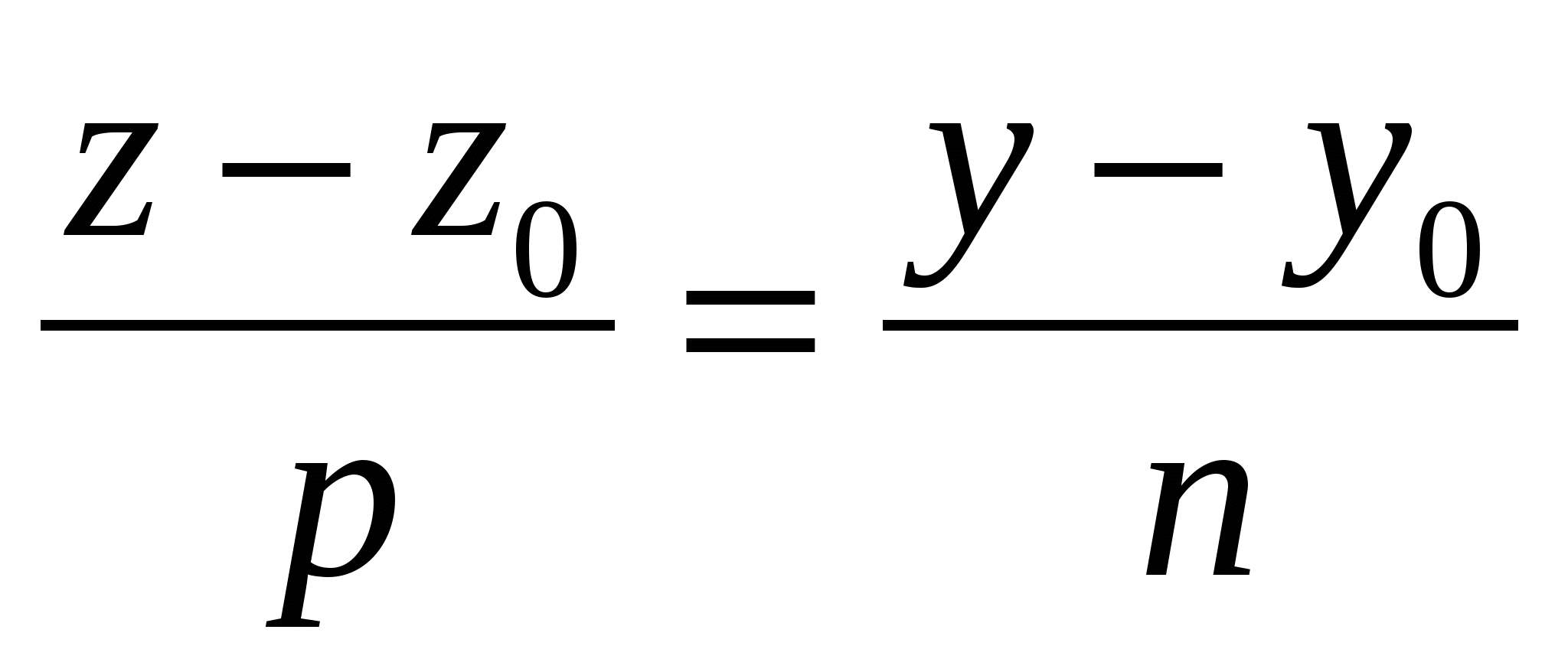 задает в пространстве … задает в пространстве …
|
1. Прямую, параллельную оси аппликат
2. Плоскость, параллельную оси ординат
3. Плоскость, параллельную оси абсцисс
4. Плоскость, параллельную осям Оу и Оz
|
|
Какая из пар плоскостей не задает прямую в пространстве
|
1. x +2y 3 z 18 = 0 и 2x +2y +3 z = 0
2. x +2y 3 z 18 = 0 и 2x + y + z +1 = 0
3. x +2y 3 z 18 = 0 и 2x + y +1 = 0
4. x +2y 3 z 18 = 0 и 2x +4y 6 z 1 = 0
|
|
Какая из заданных плоскостей перпендикулярна плоскости
x + 2y 3 z + 4 = 0 ?
|
1. 2x y + 124 = 0 2. 2x + 4y z = 0
3. x + 3y 5 z = 0 4. 2x + y z + 4 = 0
| |
 Скачать 377.5 Kb.
Скачать 377.5 Kb.