НИР. Обзор должен включать в себя введение, то есть

• Название: Обзор должен включать в себя введение, то есть
• Дата: 27.04.2022
• Размер: 221.01 Kb.
• Имя файла: 1.docx
• Тип: Обзор; #499940

Обзор должен включать в себя введение, то есть:

• 
  современное состояние исследований по научной проблеме, основные направления исследований в мировой науке;
  
• 
  актуальность решения обозначенной научной проблемы;
  
• 
  практическая значимость работы;
  
• 
  научная новизна исследования;
  
• 
  цель и задачи исследования;
  
• 
  методология и методы исследования.
  

Примерный план (может меняться по вашему усмотрению)
1. Обзор литературы

1. 
   Мёссбауэровская спектроскопия
   
   1. 
      Мёссбауэровский спектр
      

Основы мессбауэровской спектроскопии были разработаны в 1957 году Рудольфом Мёссбауэром, когда он обнаружил эффект, который сегодня носит его имя " Эффект Мёссбауэра " и который принес ему Нобелевскую премию по

физике в 1961 году. Этот вид спектроскопии стал общепризнанным методом

исследования физических свойств твердых тел, жидкостей и даже газов [17], последние два исследовались при низких температурах для получения твердой структуры. Мёссбауэровская спектроскопия, благодаря своей беспрецедентной по своим характеристикам разрешающей способности порядка 10⁻¹¹, позволяет сегодня использовать её не только в физике, но и в широких отраслях химии, биологии, геологии, промышленности и даже медицине.

Во-первых, заметим, что точно так же, как электронное окружение атома обладает энергетическими уровнями, так и ядра атомов испытывают различные переходы энергетических уровней, обычно связанные с излучением или поглощением гамма-излучения. На эти уровни энергии влияет их электрическое и магнитное окружение, которое может изменять или расщеплять эти уровни энергии. Таким образом, из этих изменений можно получить информацию о химическом окружении атомов в системе.

Эффект Мёссбауэра заключается в возбуждении атомного ядра гамма- излучением, излучаемым химическим элементом, у которого ядерные переходы (уровни атомной энергии) равны или достаточно близки к уровням энергии поглощающего атома. Резонансный процесс поглощения и излучения известен как ядерный резонанс. Для получения гамма-излучения с определенной энергией и создания резонансного эффекта необходимо, чтобы как в излучателе, так и в приемнике не было потерь энергии на отдачу, поэтому мёссбауэровскую спектроскопию можно использовать для исследования веществ и соединений, которые имеют достаточно высокую вероятность испускания и поглощения без потери энергии на отдачу. Эта вероятность высока для твердых тел. Таким образом, мессбауэровская спектроскопия основана на ядерном резонансном поглощении без отдачи и эмиссии гамма- излучения от ядер источника без потери энергии. [18].

Условие возникновения резонанса выполняется тогда, когда ядра поглотителя или источника имеют жесткую связь с окружающими его атомами

кристаллической решетки твердого тела (или молекулы). В этом случае

возникает отличная от нуля вероятность испускания или поглощения гамма квантов без потери энергии на отдачу, т.е. без возбуждения фононного спектра вещества. На рисунке 2 показан спектр эмиссии -лучей Ir¹⁹¹ с энергией 129 кэв,испускаемых ядрами в металлическом иридии при низкой температуре [19]. Узкий пик на спектре соответствует процессу испускания без отдачи.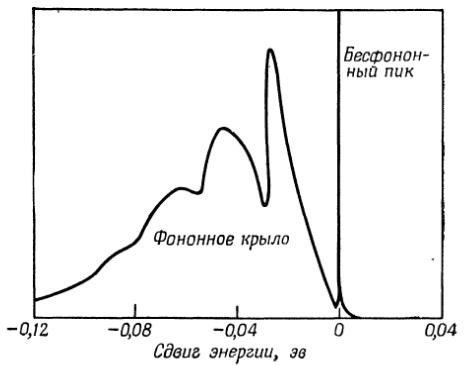



Рисунок 2 - Спектр эмиссии -лучей Ir¹⁹¹ с энергией 129 кэв, испускаемых ядрами в металлическом иридии при низкой температуре[18]

Мёссбауэровский спектр обычно регистрируется путем изменения энергии γ лучей источника и измерения резонансного поглощения (ядерного) как функции энергии γ лучей [50]. Мессбауэровский источник γ-лучей состоит из излучающих ядер в возбужденном состоянии, внедренных в кристаллическую матрицу, которая имеет относительное движение со скоростью 𝑣 по отношению к образцу. Это небольшое движение (мм/с) необходимо для того, чтобы можно было настроить энергию γ-лучей (Eγ) источника в резонанс с расщеплением ядерных уровней в поглотителе. Это изменение энергии получают с помощью небольшого доплеровского сдвига

𝜀 = (𝑣/𝑐)𝐸𝛾. Значения Eγ источника и образца совпадают при определенной скорости, резонансное поглощение достигнет максимума, а количество зарегистрированных гамма квантов, прошедших через поглотитель, достигает минимума. При более высоких или более низких скоростях резонанс будет уменьшаться до тех пор, пока скорость счета регистрируемых квантов не будет изменяться [51].

Самый простой вид мёссбауэровского спектра для ядер, имеющих только один резонансный переход, показан на рисунке 1.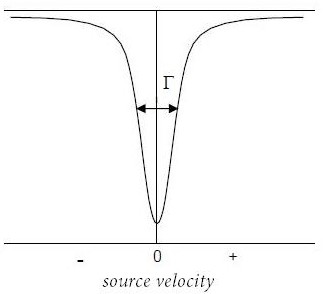



Рисунок 1 - Мёссбауэровский спектр поглощения в зависимости от допплеровского сдвига[18]

Форма линии поглощения легко определяется. Если вероятность излучения без отдачи источника – это f_{f, ,} а излучение имеет ширину линии Г, то число регистрируемых квантов около резонансной энергии Eγ рассчитывается по формуле Брейта-Вигнера:

𝑓𝑓Г 𝑑𝐸 𝑁(𝐸)𝑑𝐸 = 2𝜋 2 Г 2 (𝐸 − 𝐸γ) + (2)

( 1 )

Это распределение является распределением Лоренца, где 𝑁(𝐸) – число переходов между 𝐸 и 𝐸 + 𝑑𝐸. Точно такую же форму имеет вероятность резонансного поглощения, определяемая как:

Г 2 ( ) 𝜎(𝐸) = 𝜎0 2 2 Г 2 (𝐸 − 𝐸γ) + (2)

( 2 )

где 𝜎₀ - ядерная константа, называемая поперечным сечением резонансного поглощения, определяется по формуле:

ℎ𝑐 2 2𝐼 + 1 1 𝜎 = ( ) 𝑒 0 𝐸γ 2𝐼𝑏 + 1 1 + 𝛼

( 1 )

где 𝐼_𝑏 и 𝐼_𝑒 соответственно - ядерный спин основного состояния и возбужденного состояния, а α - это константа внутренней конверсии гамма- перехода [19].
Для применения мёссбауэровской спектроскопии необходимо учитывать, что анализируемый образец должен содержать химические элементы, которые имеют доступные мессбауэровские источники. Поэтому не каждый образец может быть проанализирован, если нет соответствующего мёссбауэровского источника. Например, если мы захотим проанализировать образец, содержащий железо, будет невозможным применение мёссбауэровского спектрометра, который использует радиоактивный источник олова (¹¹⁹Sn).

Для наблюдения эффекта Мёссбауэра должны быть выполнены несколько требований:

• 
  Энергия γ-квантов должна быть в энергетическом диапазоне от 10 до 150 кэВ, предпочтительно менее 50 кэВ, поскольку вероятность эффекта
  

Мёссбауэра f и сечение резонансный поглощения 𝜎₀ уменьшаются по мере роста Eγ.

• 
  Период полураспада первого возбужденного состояния ядра, определяющего ширину линии, должен составлять от 1 до 100 нс, потому что если она больше, то она будет очень узкой, и любая механическая вибрация может разрушить резонанс, если же, наоборот, она меньше, то линия настолько широка, что может скрыть сверхтонкие взаимодействия.
  
• 
  Для практического использования мёссбауэровский источник должен иметь радиоактивный изотоп с достаточно большим периодом полураспада за счет предшествующего распада (обычно, бета распад).
  

2. 
   Мёссбауэровские изотопы
   

Мёссбауэровский изотоп должен иметь как можно большую распространенность в природной смеси (для изотопа ⁵⁷Fe она порядка 2.19%).

В наиболее популярный в мёссбауэровской спектроскопии изотоп это

⁵⁷Fe. Радиоактивным источником для ⁵⁷Fe является изотоп ⁵⁷Co. Изотоп ⁵⁷Co

распадается за счет электронного захвата, в результате ядро оказывается в состоянии с энергией 116.6 кэВ возбужденного уровня ядра ⁵⁷Fe. Из этого состояния ядро переходит на уровень первого возбужденного состояния (𝐼_𝑒=1/2), а затем распадается до основного состояния (I_b = ½), испуская гамма-

фотон с энергией 11.1 КэВ [50] как показано на рисунке 1.



Рисунок 1 - Схема распада 57Co

Время жизни этого состояния составляет порядка τ = 100 наносекунд, поэтому ширина линии Г = 1.67 ∗ 10⁻⁹ эВ. Вследствие этого с помощью эффекта Мёссбауэра можно обнаружить сдвиг мёссбауэровской линии на половину экспериментальной ширины, т.е:

∆𝐸 Г/2 1.67x10−9(𝑒𝑉) = = = 0.12𝑥10−12 𝐸γ 𝐸γ 11.1𝑥101(𝑒𝑉)

( 1 )

Эта точность дает мёссбауэровской спектроскопии высокий потенциал в исследовании сверхтонких взаимодействий при анализе образцов.

3. 
   Сверхтонкое взаимодействие
   
   1. 
      Изомерный сдвиг
      

В мёссбауэровской спектроскопии используется практически монохроматический пучок излучения, позволяющий измерять очень малые смещения и расщепления уровней энергии, вызванные сверхтонкими взаимодействиями резонансного ядра с электронным окружением в исследуемом материале. Различают три основных взаимодействия:

1. 
   Кулоновское взаимодействие электронных и ядерных зарядов, а также сдвиг, порождаемый разницей в размерах ядра в основном и возбужденном состояниях [19]. В мёссбауэровском спектре это проявляется как сдвиг линии поглощения от нулевой скорости и называется изомерным сдвигом.
   
2. 
   Электрическое квадрупольное взаимодействие между ядерным квадрупольным моментом и тензором градиента электрического поля [12], созданным электронным окружением в ядре. Этот эффект приводит, в случае ⁵⁷Fe, к расщеплению линии резонанса на два пика.
   
3. 
   Магнитное дипольное взаимодействие между магнитным моментом ядра и внутренним или внешним магнитным полем [19]. В результате в спектре наблюдается расщепление резонансной линии на шесть линий в случае ⁵⁷Fe.
   

Изомерный сдвиг обусловлен кулоновским взаимодействие между электронами и ядром. В модели точечных зарядов, это взаимодействие не приводит к изменения энергии уровней, когда ядро распадается из возбужденного состояния в основное состояние [19, 11]. Однако, ядро имеет конечный размер, и если оно имеет разный значения для основного и возбужденного состояния, то это обстоятельство приводит к небольшому смещению линии поглощения по сравнению со случаем, когда размер ядра был бы одинаков в этих состояниях.

В мёссбауэровских экспериментах сравнивают энергетическую разницу ядерных переходов между источником и образцом, по этой причине наблюдаемый изомерный сдвиг определяется выражением:

1 𝛥𝑅 2 2 𝛿 = 𝑍𝑒2𝑅2 (|𝑇𝑠(0) | − |𝑇𝑠(0) | ) 5𝜀0 𝑅 𝐴 𝑓

( 5 )

где 𝑍 – атомный номер, 𝑒 – заряд электрона, 𝜀₀ – диэлектрическая

проницаемость вакуума, R – радиус ядра, |𝑇

² и |𝑇

2

| – плотности s (и

𝑠⁽0⁾_𝐴^|

𝑠⁽0⁾_𝑓

p1/2) электронов в источнике и поглотителе, соответственно.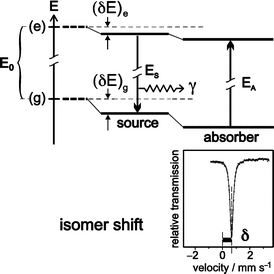



Рисунок 11 - Схема изомерного смещения для мёссбауэровских ядер[50]

Все ядра со спином (I) больше ½ состоят из несферического распределения электрического заряда [51]. Вследствие этого такие ядра обладают ядерным квадрупольным моментом. Взаимодействие квадрупольного момента ядра с градиентом электрического поля на ядре приводит к расщеплению уровней энергии. Распределение заряда характеризуется величиной, называемой градиентом электрического поля (∇ 𝐸).

𝜕2𝑉 ∇ 𝐸 = −𝑉𝑖𝑗 = 𝜕𝑥 𝜕𝑦 𝑖 𝑗

( 6 )

Когда параметр асимметрии (η) равен нулю, отсутствует разница между компонентом 𝑉_𝑥 и 𝑉_𝑦 градиента электрического поля. Энергия ядерных уровней определяется в этом случае выражением:

𝑒2𝑞𝑄 2 2 𝐸𝑄 = 1𝐼(2𝐼 − 1) (1𝑚𝑧 − 𝐼(𝐼 + 1) )

( 7 )

где 𝑄 – ядерный квадрупольный момент, 𝑒²𝑞𝑄 известен как константа квадрупольного взаимодействия, I – ядерный спин 𝑚_𝑧 – спиновое квантовое число, которое может принимать значения I , I-1,…, -I.

2. 
   Электрическое квадрупольное вз-е
   

На рисунке 8 показан пример мёссбауэровского спектра для ⁵⁷Fe. Возбужденное состояние (𝐼𝑒 = 1/2) расщепляется на два подуровня, создавая

частичное вырождения: один для 𝑚_𝑧

= ± ¹

2

(энергия +𝑒2𝑞𝑄/1) и другое для

𝑚_𝑧 = ± 1/2 (энергия −𝑒2𝑞𝑄/1 ). Следует отметить, что для основного состояния (𝐼𝑏 = 1/2) расщепление не происходит. По этой причине результирующий спектр представляет собой дублет, состоящий из двух линий, отстоящих друг от друга, на энергию, равную:

Δ𝐸 = 𝐸 (± 1⁄ ) − 𝐸 (± 1⁄ ) = 𝑒𝑄 𝑉𝑧𝑧 𝑄 𝑄 2 𝑄 2 2

( 8 )

Этот параметр называется квадрупольным расщеплением.


Рисунок 12 - Мёссбауэровский спектр ядра ⁵⁷Fe при наличии квадрупольного взаимодействия[18]
При наличии магнитного поля на ядре, магнитный момент ядерного спина взаимодействует с магнитным полем, что приводит к Зеемановскому расщеплению ядерных подуровней [51]. Магнитное поле может быть создано собственными электронами ядра, а также спинами окружающих его лигандов, участвующих в обменном взаимодействии. Магнитное поле на ядре можно также создать, накладывая сильное внешнее магнитное поле.

Гамильтониан, описывающий дипольно-магнитное взаимодействие, определяется выражением:

𝐇 = −𝜇. 𝐻 = −𝑔𝜇𝑁𝐼. 𝐻

( 9 )

где μ – ядерный магнитный момент, I – ядерный спин, g – ядерный коэффициент Ланде (𝑔 = 𝜇 / 𝐼 𝜇_𝑁) и 𝜇_𝑁 – ядерный магнетон Бора. Предполагая, что Hнаправлен вдоль оси z, собственные значения Гамильтониана определяются как:

𝜇. 𝐻𝑚𝑧 𝐸𝑚 = − 𝐼 = −𝑔𝜇𝑁𝐼. 𝐻𝑚𝑧

( 10 )

где 𝑚_𝑧 – собственное значение 𝐼_𝑧 (𝑚_𝑧 = I, I-1,…, -I); т.е. взаимодействие полностью разрушает вырождение и расщепляет уровень со спином I на 2I+1 подуровни. Правила отбора в случае магнитных дипольных переходов (𝑚𝑧 = 0, ±1), определяют количество наблюдаемых линий. Например, в случае ⁵⁷Fe, ядерные переходы между состояниями I_e=1/2 в I_b=1/2 может произойти только в шести из восьми возможных переходов (рисунок 11).



Рисунок 11 - Мёссбауэровский спектр для α-Fe[50]

3. 
   Магнитное сверхтонкое
   

2. 
   Роль железа в организме
   
   1. 
      Гемоглобин и прочие железосодержащие белки
      
   2. 
      Железо и его метаболизм
      
   3. 
      Цикл эритроцитов
      
   4. 
      Железодефицитная анемия
      
   5. 
      Препараты для поддержания статуса железа в крови (пищевые добавки и витамины)
      
      1. 
         Фумарат железа
         
      2. 
         Сульфат Железа
         
      3. 
         Хелаты железа
         

3. 
   Мёссбауэровская спектроскопия препаратов от анемии
   
   1. 
      Мёссбауэровские исследования фумарата железа (II)
      
   2. 
      Сульфатов
      
   3. 
      Хелатов