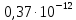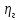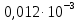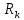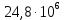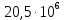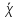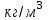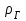Определить коэффициенты водонасыщенности и газоотдачи и их динамику с использованием функции БаклиЛеверетта
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ НЕФТИ И ГАЗА ИМ М. С. ГУЦЕРИЕВА Кафедра разработки и эксплуатации нефтяных и газовых месторождений Курсовая работа по дисциплине: «Подземная гидромеханика» на тему: «Определить коэффициенты водонасыщенности и газоотдачи и их динамику с использованием функции Бакли-Леверетта» Вариант № 4 Выполнил Валиева А.И. Проверил Борхович С. Ю Доцент к.т.н Ижевск, 2022 СОДЕРЖАНИЕ Введение…………………………………………………………………………...3 Теоретическая часть…………………………………………………………..4 Методика определения коэффициентов водонасыщенности и газоотдачи с использованием функции Бакли-Леверетта ………………4 Расчетная часть………………………………………………………………10 Задаться функциями для фазовой проницаемости в системе “газ-вода”…………………………………….....................................................11 Построить функцию Бакли-Леверетта, ее первую производную ………………………..................................................................................13 Определить искомые коэффициенты на конец безводной эксплуатации и на конец разработки залежи……………………………………………14 Выводы…………………………………………………………………………...15 Список использованной литературы…………………………………………...16 ВВЕДЕНИЕ Огромное значение при разработке месторождений углеводородов имеет понимание процессов, происходящих с течением времени в разрабатываемых пластах. Одним из таких процессов является процесс заводнения и чтобы прогнозировать показатели разработки необходимо помимо модели самого плаcта, использовать также гидродинамическую модель процесса заводнения пласта и затем применительно к конкретной системе разработки – расчетную схему для месторождения в целом или его элемента. Для большинства пластов при вытеснении из них нефти водой характерно возникновение в порах раздробленных, диспергированных глобул нефти. В местах пористых сред, где путь движению нефти преграждается плотными скоплениями зерен породы (в тупиковых зонах в поровых ловушках), остаточная нефть сохраняется в виде неподвижных глобул, не извлекаемых из пористой среды даже при ее бесконечной промывки. Возникновению неподвижных глобул способствуют также различие вязкостей нефти и воды и наличие у нефти неньютоновских свойств. Диспергирование нефти в пористых средах происходит недалеко от фронта вытеснения, позади него, где находятся одновременно нефть вода, так что за водный период из образцов рассматриваемых пористых сред добывают небольшое количество нефти. В таких случаях для описания процесса вытеснения нефти водой используют модель поршневого вытеснения. Если в пористой среде содержится сравнительно небольшое число тупиковых зон в единице объема, то нефть, будучи даже раздробленной позади фронта вытеснения ее водой, продолжает двигаться в этой среде и извлекаться из нее по мере закачки в образец воды. Существенное значение для разработки здесь имеет водный период добычи нефти, в течение которого в пористой среде происходит совместная (двухфазная) фильтрация нефти и воды. Для расчета показателей разработки в этом случае используется модель непоршневого вытеснения нефти водой, в основе которой лежат зависимости фазовых или относительных проницаемостей для нефти и воды от насыщенности пористой среды водой. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Методика определения коэффициентов водонасыщенности и газоотдачи с использованием функции Бакли-Леверетта По схеме Баклея - Леверетта предполагается в пласте движущийся фронт вытеснения. Перед фронтом вытеснения движется только нефть, позади него — одновременно нефть и вода со скоростями, пропорциональными соответствующим фазовым проницаемостям. Причем по мере продвижения фронта вытеснения скорости изменяются не только в зависимости от насыщенности в пласте, но и во времени. В момент подхода фронта к скважине происходит мгновенное обводнение до некоторого значения, соответствующего скачку нефтенасыщенности на фронте Sф , а затем обводненность медленно нарастает. 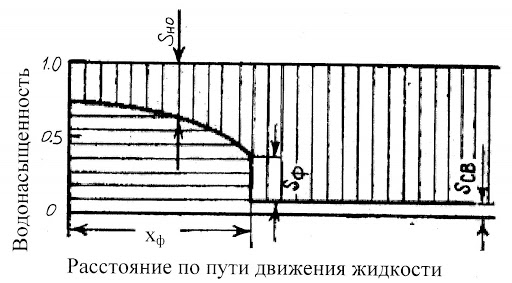 Рис. 1. Модель непоршневого вытеснения. Теория непоршневого вытеснения нефти основана на зависимости проницаемости породы для движущихся фаз от насыщенности порового пространства той или иной фазой. Баклей — Леверетт ввели понятие Которое является аналогом обводненности продукции скважин 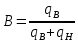 Функция Бакли – Леверетта f(σ) зависит от водонасыщенности σ, определяется следующим образом: 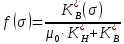  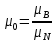 Функция f(σ) строится индивидуально для каждого типа коллектора (песчаников, алевролитов, известняков) 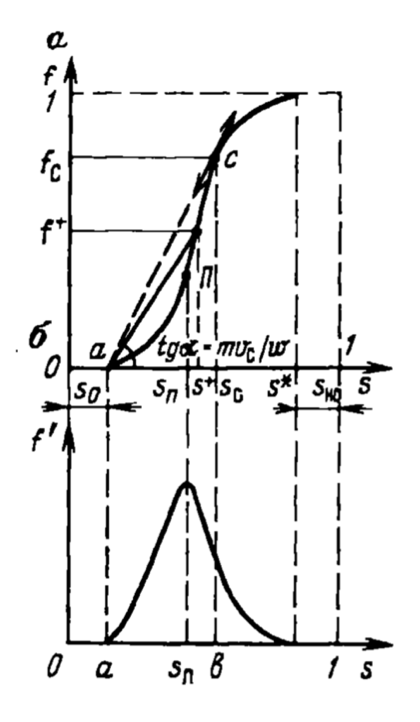 Рис. 2. Зависимость объемной доли вытесняющей фазы (воды) в потоке f(σ) и ее производной от насыщенности Модель Баклея-Леверетта Дифференциальное уравнение в частных производных первого порядка для определения насыщенности: 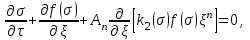 (1) (1)где п = 0,1/2 — соответственно для случаев прямолинейно-параллельного и радиального вытеснения. Без учета силы тяжести (Ап = 0 в (1)) двухфазная фильтрация для случая прямолинейно-параллельного вытеснения рассматривалась С. Баклеем и М. Левереттом в 1942 г., а позже независимо от них А. М. Пирвердяном, исследовавшим также случай более общего закона фильтрации при двухфазном течении. Задачи двухфазной фильтрации без учета капиллярных сил, основанные на решении уравнений типа (1) при соответствующих начальном и граничных условиях, известны как задачи (модель) Баклея—Леверетта. Задачи вытеснения такого типа в одномерной постановке изучены достаточно полно. В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание. Для обоих случаев одномерного потока (прямолинейно-параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта, описываемой однотипным уравнением для насыщенности σ вытесняющей фазы, которое получается из (1) при гравитационном параметре Ап = 0 и имеет вид 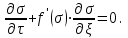 (2) (2)Здесь использовано преобразование 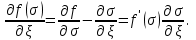 Безразмерные независимые переменные 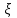 и и 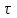 , можно представить в единой форме для обоих одномерных потоков и обобщить на случай, когда суммарный «удельный» расход qфаз зависит от времени. Имеем , можно представить в единой форме для обоих одномерных потоков и обобщить на случай, когда суммарный «удельный» расход qфаз зависит от времени. Имеем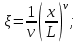 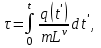 (3) (3)где L— характерный линейный размер; 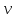 = 1,2 — соответственно для линейного и радиального течений, причем в последнем случае пространственная координата х = r(r— расстояние от точки пласта до скважины), a L = Rк; q (t) = = 1,2 — соответственно для линейного и радиального течений, причем в последнем случае пространственная координата х = r(r— расстояние от точки пласта до скважины), a L = Rк; q (t) = 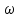 (t) или q(t) = Q(t)/(2 (t) или q(t) = Q(t)/(2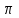 h) соответственно для линейного и радиального вытеснения; h) соответственно для линейного и радиального вытеснения; 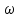 (t) — суммарная скорость фильтрации фаз; Q (t) — суммарный объемный расход; т и h— соответственно коэффициент пористости и толщина пласта. (t) — суммарная скорость фильтрации фаз; Q (t) — суммарный объемный расход; т и h— соответственно коэффициент пористости и толщина пласта.Хотя переменные 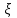 и и 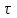 имеют смысл безразмерных объемов, будем для простоты называть их соответственно пространственной и временной переменными. Напомним, что функция f(σ), входящая в уравнение (2), определяется через относительные фазовые проницаемости ki(σ). имеют смысл безразмерных объемов, будем для простоты называть их соответственно пространственной и временной переменными. Напомним, что функция f(σ), входящая в уравнение (2), определяется через относительные фазовые проницаемости ki(σ).В рассматриваемом случае f(σ), называемая функцией Баклея— Леверетта или функцией распределения потоков фаз, имеет простой физический смысл. При Δр = 0 и р'к (σ) = 0 находим для скорости фильтрации 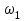 вытесняющей фазы соответственно в случае прямолинейно-параллельного и радиального вытеснения вытесняющей фазы соответственно в случае прямолинейно-параллельного и радиального вытеснения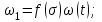 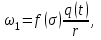 (4) (4)тогда имеем 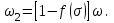 Отсюда следует, что f(σ), представляющая в силу (4) отношение скорости фильтрации 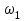 вытесняющей фазы к суммарной скорости вытесняющей фазы к суммарной скорости 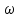 , равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз. , равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз.Функция Баклея—Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту. Задачи повышения нефте- и газоконденсатоотдачи в значительной степени сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f(σ) в направлении увеличения полноты вытеснения. Типичные графики функции f(σ)и ее производной 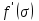 изображены на рис. 2. С ростом насыщенности f(σ) монотонно воз растает от 0 до 1. изображены на рис. 2. С ростом насыщенности f(σ) монотонно воз растает от 0 до 1.Характерной особенностью графика f(σ)является наличие точки перегиба σп, участков вогнутости и выпуклости, где вторая производная 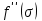 соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта. Зависимость функций f(σ) и соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта. Зависимость функций f(σ) и 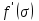 от отношения вязкостей фаз от отношения вязкостей фаз 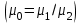 показана на рис. 3. показана на рис. 3.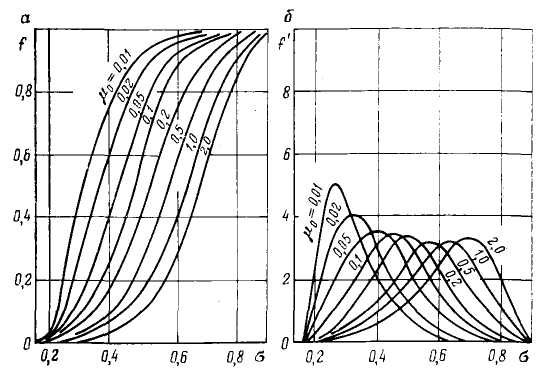 Рис. 3 - Графики функции Баклея—Леверетта (а) и ее производной (б) для различных отношений вязкостей 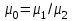 Для описания и расчета процесса вытеснения к уравнению (2) нужно добавить начальное и граничное условия при 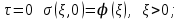 при 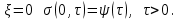 (5) (5)Первое из условий (5) означает, что в момент времени τ = 0 (до начала процесса вытеснения) в пласте имеется некоторое известное распределение насыщенности σ вытесняющей фазы, определяемое функцией 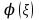 . Согласно второму условию (5), при τ > 0 в пласт через нагнетательную скважину или галерею, расположенную на «линии» . Согласно второму условию (5), при τ > 0 в пласт через нагнетательную скважину или галерею, расположенную на «линии» 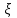 = 0, закачивается вытесняющая жидкость, насыщенность которой при = 0, закачивается вытесняющая жидкость, насыщенность которой при 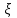 = 0 меняется со временем по заданному закону = 0 меняется со временем по заданному закону 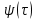 . В ряде случаев можно считать, что . В ряде случаев можно считать, что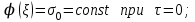 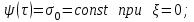 (6) (6)Это случай кусочно-постоянных начальных данных, имеющий важное значение для практических приложений. Величина начальной водонасыщенности σ0влияет на процесс заводнения и определяет структуру зоны вытеснения. РАСЧЕТНАЯ ЧАСТЬ
2.1 Задаться функциями для фазовой проницаемости в системе “газ-вода” Запишем основной закон фильтрации Дарси для прямолинейного движения в случае совместной фильтрации: 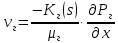 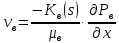 Вытеснение газа водой из пласта происходит в соответствии с вытеснением по модели непоршневого вытеснения. Относительные проницаемости для газа и воды, зависящие от водонасыщенности s, выражаются следующими формулами: 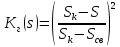 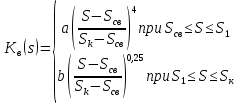 Прежде всего необходимо определить численные значения коэффициентов а и b, входящих в приведенные зависимости 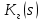 и и 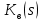 Так, значение коэффициента b находим из условия (см рис 1) 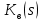 =1. Имеем =1. Имеем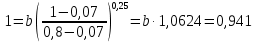 Значение коэффициента a установим из условия 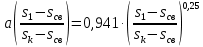 Отсюда 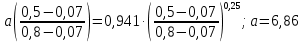 Таблица 1 - Зависимость относительных проницаемостей нефти kн(s) и воды kв(s), f(s) от водонасыщенности s
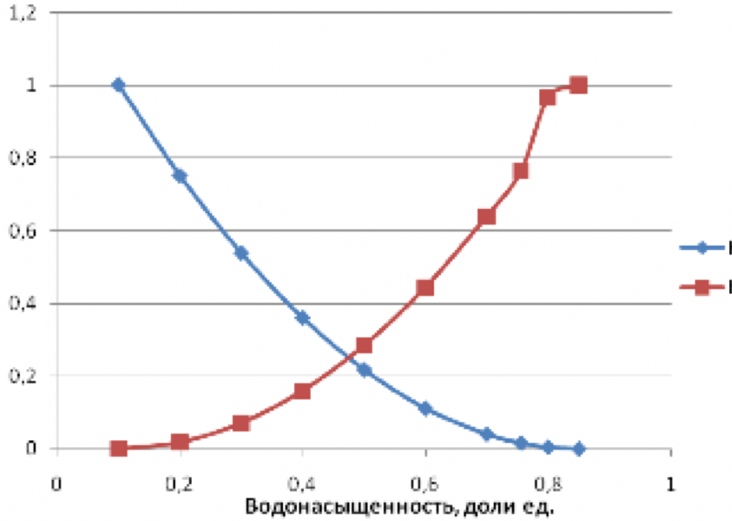 Рис. 4 - Зависимость относительных проницаемостей для нефти и воды от насыщенности 2.2 Построить функцию Бакли-Леверетта, ее первую производную В соответствии с теорией фильтрации неоднородных жидкостей распределение водонасыщенности в пласте при 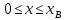 находят следующим образом находят следующим образом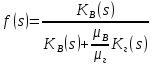 Водонасыщенность на фронте вытеснения нефти водой, т.е. при 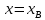 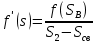 При этом 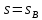 при x = 0. Из кривых относительных проницаемостей имеем также, что при x = 0. Из кривых относительных проницаемостей имеем также, что 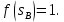 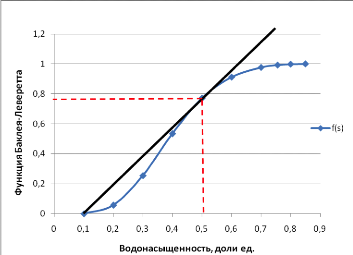 Рисунок 5 - Зависимость f(s) от s 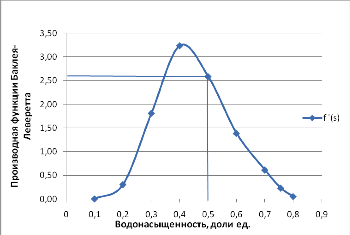 Рисунок 6 - Зависимость f’’(s) от s 2.3 Определить искомые коэффициенты на конец безводной эксплуатации и на конец разработки залежи Распределение водонасыщенности в пласте можно найти аналитическим путем из соотношений, подставив заданные относительные проницаемости в функцию f(s) Однако такой метод определения распределения насыщенности довольно сложный. Проще найти распределение насыщенности графоаналитическим методом. Так соотношение тангенс угла наклона касательной, проведенной из точки 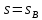 на графике, представленном на рисунке 5, к кривой f(s), т.е. на графике, представленном на рисунке 5, к кривой f(s), т.е.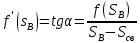 где f(Sв) - значение функции, определяемое по графику (рисунок 5); Sв - водонасыщенность на фронте вытеснения; Sсв - насыщенность связанной водой. Проведя касательную к кривой f(s) из точки 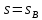 получим что получим что 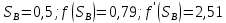 ВЫВОД Решением Бакли - Леверетта широко пользуются в нефтяной и газовой промышленности для расчета эффективных фильтрационных характеристик вытеснения нефти водой или газом. В ходе работы мы провели численное и аналитическое решение задачи и проверили адекватность численной реализаций модели Бакли – Леверетта двухфазной фильтраций одномерного течения несжимаемых несмешивающихся жидкостей. Результаты, полученные после проведения численных расчетов вполне соответствуют аналитическому решению и качественно соответствует моделируемым процессам . Можно сделать вывод что аналитические и численные решения для задачи Бакли - Леверетта вполне применимы и их значения приблизительно совпадают. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебник для вузов. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 480 с. Басниев К.С. и др. Подземная гидромеханика. М.: Недра, 1993 г., 172-179 с. Басниев К.С. и др. Подземная гидромеханика. М.:Недра, 1993 г., 131-151 с., 159-171 с. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: Учебное пособие для вузов. - М. - Ижевск: Институт компьютерных исследований, 2005, 544 с. Подземная гидромеханика: Учебно-методическое пособие / сост. С.Ю. Борхович, И.В. Пчельников, С.Б. Колесова – Ижевск: Издательский центр « Удмуртский университет» 2017 |

 103
103