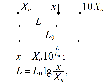Белодедов Построение графиков в Exel. Ось аргумента функции) и вертикальную (ось
 Скачать 1.09 Mb.
|
|
При подготовке научно-технических текстов практически у каждого автора возникает потребность графически представить ту или иную зависимость. В подавляющем большинстве случаев изображается зависимость значения некоторой функции (действительное число) от аргумента этой функции (действительное число). В естественно-научной среде принято представлять зависимости в виде графиков. График – это изображение на плоскости (обычно – на листе бумаги или на экране компьютера) множества точек (возможно, бесконечного множества точек), физические координаты которых несут информацию о значениях аргумента функции (то, от чего зависит) и значениях функции (то, что зависит). Физические координаты точек принято считывать в большинстве случаев – в декартовой системе координат, значительно реже – в полярной системе координат, практически никогда – в других специальных системах координат. В декартовой системе координат, как правило, рисуют две оси – горизонтальную (ось X, ось аргумента функции) и вертикальную (ось Y, ось значений функции). По оси X откладывают возможные значения аргумента функции. Эти значения откладываются в порядке возрастания слева направо. По оси Y откладывают возможные значения функции. Эти значения откладываются в порядке возрастания снизу вверх (иногда, в порядке исключения, допускается – в порядке возрастания сверху вниз). Соответствие между значением аргумента x и физической координатой деления оси l теоретически может быть любым. Однако «в рамках приличия» использовать два типа соответствия: 1. Линейная шкала. Физические координаты делений шкалы lсвязаны со значениями делений шкалы x линейной зависимостью:  . Значения шкалы выбираются равномерно – например, 0, 10, 20, 30, 40, …, или 1150, 1200, 1250, 1300, …, то есть каждое последующее деление превышает предыдущее на одно и то же значение. Это значение носит название «цена делений шкалы» и в приведённых примерах оно равно 10 и 50. Через каждое деление горизонтальной оси проводится вертикальная линия, набор этих линий составляет вертикальную сетку. Каждое деление шкалы имеет подпись – значение этого деления. Принято деления горизонтальной оси и цену деления выбирать круглыми значениями, как это сделано в приведённых примерах. Деления типа 312, 315, 318, 321, …– это дурной тон.Соседние деления линейной шкалыXn иXn+1, разность значений которых составляет цену деления, физически отстоят на графике на одинаковое расстояние. Помимо основных делений шкалы, описанных выше, иногда выполняется вертикальная сетка промежуточных делений. В этом случае промежуток между двумя соседними основными делениями равномерно разбивается на несколько интервалов (обычно – 2, 4, 5 или 10) и эти интервалы разделяются вертикальными линиями. Сетка промежуточных делений помогает точнее определить положение точки на графике. При использовании линейной шкалы связь между значением величины x и его физической координатой выглядит как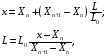 
По вертикальной оси графика в линейном масштабе точно так же откладываются основные и промежуточные деления и точно так же рисуется горизонтальная сетка графика. 2. Логарифмическая шкала. Физические координаты делений шкалы lсвязаны со значениями делений шкалы x линейной зависимостью: 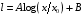 . Основание логарифма значения не имеет – оно влияет только на величину коэффициента A в приведённой формуле, поэтому в дальнейшем будем использовать десятичный логарифм.В отличие от линейной шкалы, у которой одинаковое расстояние разделяют соседние деления шкалы Xn иXn+1 с одинаковой разностью 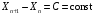 , в логарифмической шкале соседние деления шкалы, расстояние между которыми постоянно, имеют значениями Xn иXn+1, отношение которых постоянно: 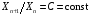 . Наиболее часто это отношение выбирают равным 10. В этом случае в логарифмической шкале связь меж-
Как и в случае линейной шкалы, при применении логарифмической шкалы на графике иногда допускаются промежуточные деления, причём их значения, как правило, обычно выбираются равными 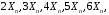 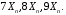 Следует отметить, что, в отличие от линейной шкалы, где промежуточные деления располагаются равномерно, в логарифмической шкале промежуточные деления располагаются сильно неравномерно. Подписи значений промежуточных значений шкалы ставить н принято ни при использовании линейной, ни при использовании логарифмической шкалы.Примеры осей с линейной шкалой и с логарифмической шкалой:
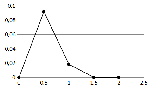
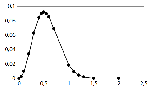
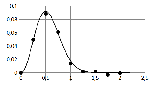
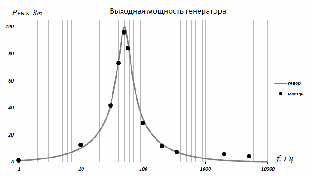
При построении графиков экспериментальных или теоретических зависимостей следует придерживаться равномерного ряда значений аргумента. В случае линейного масштаба это пожелание проблем не вызывает, в случае логарифмического масштаба равномерный ряд значений аргумента выглядит как 1, 10, 100, 1000, … (одна точка на декаду), либо 1, 3, 10, 30, 100, 300, … (две точки на декаду), либо 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000, … (три точки на декаду. Возможно также логарифмически-равномерный выбор значений из рядов: 1, 1,5, 2,2, 3,2, 4,5, 6,8, 10, 15, 22, 32, 45, 68, 100, … (ряд Е6), 1, 1,2, 1,5, 1,8, 2,2, 2,6, 3,2, 3,8, 4,6, 5,6, 6,8, 8,3, 10, 12, 15, 18, … (ряд Е12), и т.д. Каждое последующее значение ряда получается домножением предыдущего на 101/6 (ряд Е6), либо на 101/12 (ряд Е12), либо на 101/24 (ряд Е24), и т.д. Каждая ось должна быть подписана. Подпись располагается в самом конце оси (крайняя правая точка для горизонтальной оси и крайняя верхняя – для вертикальной) и должна содержать название величины, значения которой откладываются на шкале оси, и единицу измерения. Примеры подписей осей: f, кГц; K, дБ; з/пл., млн.руб.; U, 10-12 В. При этом подписи делений шкалы единицу измерения содержать не должны – только значение. Количество точек для построения не регламентируется. Точек должно быть, во-первых, столько, чтобы отразить все особенности графика, и, во-вторых, график не должен претерпевать резких изломов в своих точках. Если при построении графика обнаруживается излом в точках со значениями аргумента xn–1, xn,xn+1, следует добавить на график точки со значениями аргумента 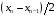 и 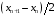 . И поступать подобным образом следует до тех пор, пока резкие изломы на графике не исчезнут. При построении графиков экспериментальных зависимостей следует отмечать каждую экспериментально полученную (измеренную) точку зависимости, после чего соединять эти точки отрезками прямых линий, без сглаживания. При построении графиков теоретических зависимостей следует вычислить значения как можно большего количества точек (вплоть до нескольких тысяч. После этого нужно каждую пару точек соединить отрезком прямой линии, не отмечая специально рассчитанные точки графика. Примеры выбора точек для построения графиков:
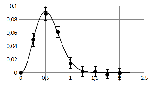
При графическом сравнении теоретической зависимости с результатами измерений на графике строится теоретическая зависимость (максимальное количество рассчитанных точек, точки не рисуются и соединяются отрезками прямых линий) и отдельно наносятся точки, соответствующие результатам измерений. На профессионально построенных графиках при этом принято отмечать погрешности измерений, как это показано на рисунке:
Рекомендуется на графиках линии различного назначения изображать различной яркости (толщины). Например, линия графика – наиболее ярко, оси – менее ярко, основная сетка – ещё менее ярко, дополнительная сетка – с наименьшей яркостью. На графике можно располагать текстовую информацию, как то: название графика, название отдельных зависимости, значения параметров, относящихся к разным зависимостям, и т.д. Сформулируем в итоге требования к графикам, выполняемым в ходе лабораторных работ: 1. График должен иметь две оси – горизонтальную (ось значений аргумента) и вертикальную (ось значений функции). 2. Каждая ось должна быть подписана. Подпись к оси должна располагаться в конце оси и должна содержать наименование величины и единицу её измерения. 3. На каждой оси должны быть основные деления с подписями их значений. Основные деления определяют основную сетку (по вертикали и по горизонтали), которая также должна быть на графике. Дополнительное требование к графикам, оформляемым к отчётам к лабораторным работам: График может быть выполнен в одном из двух вариантов: 1. На миллиметровой бумаге. Все линии и надписи выполняются от руки. Пишущий инструмент не регламентируется. Готовый график вклеивается в отчёт по лабораторной работе. 2. В виде компьютерной распечатки. Все линии и надписи выполняются при распечатке одновременно с выводом графика. Дописывания от руки не допускаются. Готовый график вставляется в текст отчёта по лабораторной работе. Программа, используемая для построения графика, не регла-ментируется. Построение графиков в программе MS Excel 7/10. В программе Excel предусмотрена возможность построения графиков. Графики в программе строятся по точкам. Координаты точек удобнее всего задавать в столбцах листа Excel. Если в одном столбце листа последовательно сверху вниз поместить значение аргумента точек графика, а в соседнем (справа) столбце – последовательно сверху вниз значения функции, то по этим координатам можно построить график. Для этого нужно выделить все введённые числа и выбрать действия Вставить/Диаграмма/Точечная. Полезное мнемоническое правило: Если Вы хотите построить график, ни в коем случае не выбирайте подпункт со словом «График»! При построении точечной диаграммы Excel предлагает варианты построения:
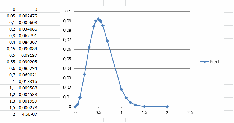
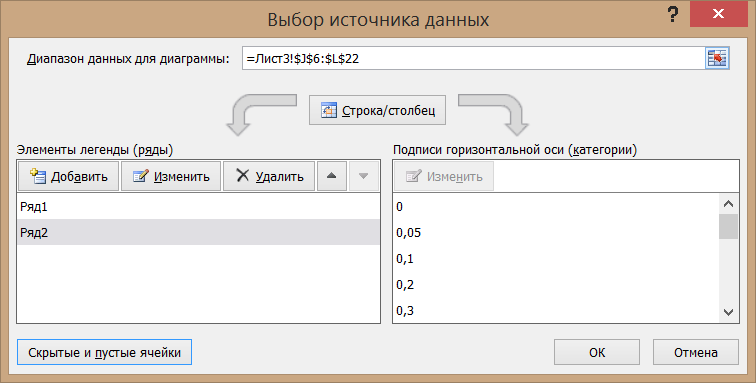
изменении размера области диаграммы деления осей и сетка автоматически изменяются, размер шрифта подписи делений остаётся неизменным. На графике обязательно должна присутствовать вертикальная сетка, которой нет по умолчанию. Чтобы её построить, достаточно выполнить правый клик по подписи любого деления оси и «Добавить основные линии сетки». Точно так же можно «Добавить промежуточные линии сетки». Легенда графика (… Ряд1) для графика, показывающего одну зависимость, является излишней, и её лучше удалить (правый клик/Удалить). Параметры построенной линии зависимости можно изменять. Для этого следует выполнить правый клик по маркеру или линии зависимости/Формат ряда данных. После этого в открывшемся диалоговом окне можно выбрать значения всех актуальных параметров: тип и цвет линии, тип и размер маркера, цвет границы маркера, цвет заливки маркера и многое другое. Очень часто в построенном графике нужно изменить параметры построения – минимальное и максимальное значения аргумента либо функции, шаг делений оси, наличие/отсутствие основных и промежуточных линий сетки, линейный/логарифмический масштаб построения и многое другое. Все эти настройки можно изменить, сделав правый клик по линии/маркеру и выбрав Формат ряда данных. Иногда возникает необходимость изобразить на одном графике несколько зависимостей. Это можно сделать двумя способами: 1. Зависимости содержат одинаковые количества точек с одинаковыми значениями аргумента. В этом случае следует в одном столбце расположить значения аргумента точек, в столбце справа – значения первой зависимости, в следующем справа столбце – значения второй зависимости, и т.д. При построении графика нужно выделить все заполненные столбцы и нажать пункт «Вставка» главного меню. 2. Зависимости содержат абсолютно независимые значения. В этом случае следует построить сначала одну зависимость стандартным методом, затем выполнить на диаграмме правый клик/Выбрать данные, в открывшемся окне нажать на «Добавить», и в новом диалоговом окне указать столбец, содержащий значения аргумента (X) и значения зависимости (Y). Кроме того, можно указать имя ряда, которое, например, будет использоваться, например, в легенде графика. Наименование и расположение данных каждого ряда можно редактировать с помощью кнопки «Изменить» справа от кнопки «Добавить». Можно также удалить зависимость кнопкой «Удалить» справа от кнопки «Изменить»:
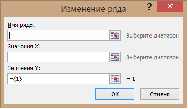
При нажатии на кнопку «Добавить» будет открыто окно «Изменение ряда», в которое необходимо внести имя нового ряда (оно будет использоваться
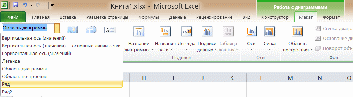
в легенде графика), колонку со значениями аргумента графика («Значения X», можно указать диапазон, можно выделить ячейки на листе вручную), и колонку со значениями функции графика («Значения Y», можно указать диапазон, можно выделить ячейки на листе вручную). После нажатия кнопки «ОК» ряд будет добавлен к графику. Все параметры всех элементов построенного графика можно редактировать. Доступ к ним открывается (при «фокусировке» на диаграмме) на вкладках «Конструктор», «Макет» и «Формат», названия всех элементов и действий с ними интуитивно понятно. Некоторую проблему иногда вызывает доступ к конкретному ряду значений на построенном графике (с целью, например, изменить цвет линии). Доступ у конкретному ряду можно получить, выполнив действия Макет/Текущий фрагмент:
и выбрав вместо «Область диаграммы» имя соответствующего ряда:
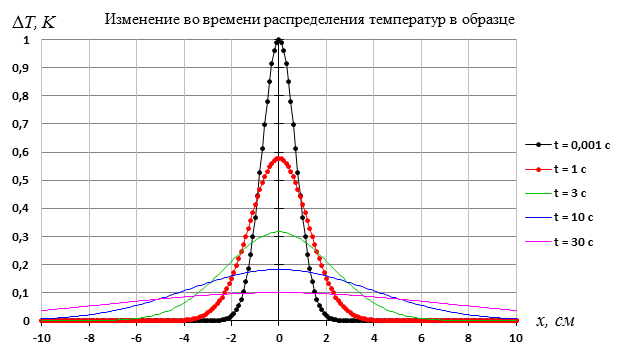
Примеры построения графиков:
|
и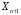 
– значения двух соседних делений оси, между которыми попадает точка на графике, x – значение точки, 
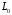– расстояние между ближайшим слева делением оси (в мм, см и т.д.), L – расстояние между соседними делениями оси (в мм, см и т.д.), как это изображено на рисунке.
