екекркер. Кодирование. Основы теории кодирования. Кодирование. Основные понятия

• Название: Основы теории кодирования. Кодирование. Основные понятия
• Анкор: екекркер
• Дата: 02.05.2022
• Размер: 0.93 Mb.
• Имя файла: Кодирование.doc
• Тип: Глава; #507638
• страница: 1 из 4

Глава 2. Основы теории кодирования.

2.1. Кодирование. Основные понятия.

Различные методы кодирования широко используются в практической деятельности человека с незапамятных времён. Например, десятичная позиционная система счисления – это способ кодирования натуральных чисел. Другой способ кодирования натуральных чисел – римские цифры, причем этот метод более наглядный и естественный, действительно, палец – I, пятерня – V, две пятерни – X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен способом кодирования основанном на позиционной десятичной системой счисления. Из этого примера можно заключить, что различные способы кодирования обладают присущими только им специфическими особенностями, которые в зависимости от целей кодирования могут быть как достоинством конкретного способа кодирования, так и его недостатком.

Широко известны способы числового кодирования геометрических объектов и их положения в пространстве: декартовы координаты и полярные координаты. И эти способы кодирования отличаются присущими им специфическими особенностями.

До XX века методы и средства кодирования играли вспомогательную роль, но с появлением компьютеров ситуация радикально изменилась. Кодирование находит широчайшее применение в информационных технологиях и часто является центральным вопросом при решении самых разных задач таких как:

– представление данных произвольной природы (чисел, текста, графики) в памяти компьютера;

– оптимальная передача данных по каналам связи;

– защита информации (сообщений) от несанкционированного доступа;

– обеспечение помехоустойчивости при передаче данных по каналам связи;

– сжатие информации.

С точки зрения теории информации кодирование — это процесс однозначного сопоставления алфавита источника сообщения и некоторой совокупнос­ти условных символов, осуществляемое по определенному правилу, а код (ко­довый алфавит) — это полная совокупность (множество) различных условных символов (символов кода), которые могут использоваться для кодирования исходного сообщения и которые возможны при данном правиле кодирования. Число же различных кодовых символов составляющих кодовый алфавит называют объемом кода или объёмом кодового алфавита. Очевидно, что объём кодового алфавита не может быть меньше объёма алфавита кодируемого исходного сообщения. Таким образом, кодирование — это преобразование исходного сообщения в совокупность или последовательность кодовых симво­лов, отображающих сообщение, передаваемое по каналу связи.

Кодирование может быть числовым (цифровым) и нечисловым, в зависимости от вида, в котором представлены кодовые символы: числа в какой-либо системе счисления или иные какие-то объекты или знаки соответственно.

В большинстве случаев кодовые символы представляют собой совокупность или последовательность неких простейших составляющих, например, последовательность цифр в кодовых символах числового кода, которые называются элементами кодового символа. Местоположение или порядковый номер элемента в кодовом слове определяется его позицией.

Число элементов символа кода, используемое для представления одного символа алфавита исходного источника сообщений, называют значностью кода. Если значность кода одинакова для всех символов алфавита исходного сообщения, то код называют равномерным, в противном случае — неравномерным. Число элементов входящих в кодовый символ иногда называют дли­ной кодового символа.

С точки зрения избыточности все коды можно разделить на неизбыточные коды и избыточные. В избыточных кодах число элементов кодовых символов может быть сокращено за счет более эффективного использования оставших­ся элементов, в неизбыточных же кодах сокращение числа элементов в кодо­вых символах невозможно.

Задачи кодирования при отсутствии помех и при их наличии существенно различны. Поэтому различают эффективное (статистическое) кодирование и кор­ректирующее (помехоустойчивое) кодирование. При эффективном кодировании ставится задача добиться представления символов алфавита источника сообщений минимальным числом элементов кодовых символов в среднем на один символ алфавита источника сообщений за счет уменьшения избыточности кода, что ведет к повышению скорости передачи сообщения. А при корректирующем (помехоустойчивом) кодировании ставится задача снижения вероятности ошибок в передаче символов исходного алфавита путем обнаружения и исправления ошибок за счет введения дополнительной избыточности кода.

Отдельно стоящей задачей кодирования является защита сообщений от несанкционированного доступа, искажения и уничтожения их. При этом виде кодирования кодирование сообщений осуществляется таким образом, чтобы даже получив их, злоумышленник не смог бы их раскодировать. Процесс такого вида кодирования сообщений называется шифрованием (или зашифровкой), а процесс декодирования – расшифрованием (или расшифровкой). Само кодированное сообщение называют шифрованным (или просто шифровкой), а применяемый метод кодирования – шифром.

Довольно часто в отдельный класс выделяют методы кодирования, которые позволяют построить (без потери информации) коды сообщений, имеющие меньшую длину по сравнению с исходным сообщением. Такие методы кодирования называют методами сжатия или упаковки данных. Качество сжатия определяется коэффициентом сжатия, который обычно измеряется в процентах и который показывает на сколько процентов кодированное сообщение короче исходного.

При автоматической обработке информации с использованием ЭВМ как правило используют числовое (цифровое) кодирование, при этом, естествен­но, возникает вопрос обоснования используемой системы счисления. Действительно, при уменьшении основания системы счисления упрощается алфавит элементов символов кода, но происходит удлинение символов кода. С другой стороны, чем больше основание системы счисления, тем меньшее число разрядов требуется для представления одного символа кода, а, следовательно, и меньшее время для его передачи, но с ростом основания системы счисления существенно повышаются требования к каналам связи и техническим средствам распознавания элементарных сигналов, соответствующих различным элементам символов кода. В частности, код числа, записанного в двоичной системе счисления в среднем приблизительно в 3,5 раза длиннее десятичного кода. Так как во всех системах обработки информации приходится хранить большие информационные массивы в виде числовой информации, то одним из существенных критериев выбора алфавита элементов символов числового кода (т.е. основания используемой системы счисления) является минимизация количества электронных элементов в устройствах хранения, а также их простота и надежность.

При определении количества электронных элементов требуемых для фиксации каждого из элементов символов кода необходимо исходить из практически оправданного предположения, что для этого требуется количество простейших электронных элементов (например, транзисторов), равное основанию системы счисления a. Тогда для хранения в некотором устройстве n элементов символов кода потребуется M элементов:

M =a·n. (2.1)

Наибольшее количество различных чисел, которое может быть записано в этом устройстве N:

N = aⁿ .

Прологарифмировав это выражение и выразив из него n получим:

n= ln N / ln a.

Преобразуем выражение (2.1) к виду

M= a ∙ ln N / ln a. (2.2)

Определим, при каком основании логарифмов aколичество элементов M будет минимальным при заданном N. Для этого продифференцируем по aфункцию M = f(a) и ее производную приравняем нулю:

= 0.

Очевидно, что для любого конечного a
ln N / ln² a ≠ 0

и, следовательно,

ln a -1 = 0,

откуда a = e ≈ 2,7.

Так как основание системы счисления может быть только целым числом, то а выбирают равным 2 или 3. Для примера зададимся максимальной емкостью устройства хранения N=10⁶ чисел. Тогда при различных основаниях систем счисления (а)количество элементов (M)в таком устройстве хранения будет, в соответствии с выражением (2.2), следующие (Таблица 2.1):

Таблица 2.1.

а	2	3	4	5	10	20
М	39,2	38,2	39,2	42,9	60	91,2

Следовательно, если исходить из минимизации количества оборудова­ния, то наиболее выгодными окажутся двоичная, троичная и четверичная системы счисления, которые близки по этому параметру. Но так как техническая реализация устройств, работающих в двоичной системе счисления, значительно проще, то наибольшее распространение при числовом кодировании получили коды на основе системы счисления по основанию 2.

2.2. Избыточность кодов.

Понятие избыточности означает, что фактическая энтропия кода или сообщения (Н) меньше, чем максимально возможная энтропия (H_max), т. е. число символов в сообщении или элементов в символе кода больше, чем это требовалось бы при полном их использовании.

Понятие избыточности легко пояснить следующим примером.

Выделение полезного сигнала на уровне помех — одна из основных проблем передачи информации. Одним из путей повышения надёжности передачи сообщений может быть передача дополнительных символов, т.е. повышение избыточности сообщений.

Действительно, по теореме Котельникова (§ 1.7), непрерывное сообщение (сигнал) можно передать последовательностью мгновенных отсчетов его значений с промежутками между ними :



где f_max – верхняя граничная частота в спектре сигнала.

При наличии помех промежутки между отсчетами (Δt_n) необходимо уменьшать, т.е.


В этом случае мы увеличиваем число отсчетов и, следовательно, увеличиваем избыточность сообщения и тем самым повышаем его помехозащищенность.

Пусть сообщение из nсимволов содержит количество информации I. Если сообщение обладает избыточностью, то его (при отсутствии шума) можно передать меньшим числом символов n₀(n₀< n). При этом, количества информации (I₁и I_1max), приходящиеся на один символ сообщения, будут связаны соотношением:

I₁ = I/n < I_1max = I/n₀

и, следовательно,

n ∙ I₁ = n₀∙ I_1max.

За меру избыточности принимается величина R: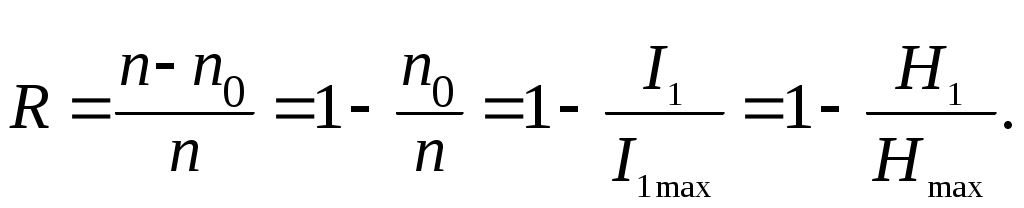

(2.3)

Таким образом, избыточность — это свойство, характеризующее возможность представления тех же сообщений в более экономной форме.

При кодировании избыточных сообщений возникает определенная исходная избыточность кодов. Наличие исходной избыточности уменьшает пропускную способность каналов и увеличивает формат сообщений. Вместе с тем в процессе передачи информации избыточность сообщений и кодов является средством, полезным для борьбы с внешними возмущающими воздействиями и помехами.

По наличию избыточности коды также делятся на избыточные и неизбыточные. Для неизбыточных кодов характерно то, что они позволяют просто определить различные символы сообщения. Переход от неизбыточного кода к избыточному осуществляется путем добавления позиций в кодовых симво­лах, которые можно получить либо путем различных логических операций, выполняемых над основными информационными позициями, либо путем ис­пользования алгоритмов, связывающих неизбыточный и избыточный коды. Например, если есть символы сообщения А₁; А₂; А₃; А₄, то их можно закодировать в двоичном неизбыточном коде:

А₁ = 00; А₂ = 01; А₃ = 10; А₄ = 11.

Для получения избыточного кода можно ввести еще одну позицию, значение которой будет определяться как сумма значений предшествующих символов по модулю два:

А₁ = 000; А₂ = 011; А₃ = 101; А₄ = 110.

Особенностью такого кода является то, что он позволяет обнаружить любую единичную ошибку (ошибку в одной из позиций кода), выявившуюся в процессе передачи кода.

2.3. Эффективное кодирование равновероятных символов сообщений.

Эффективное кодирование используется в каналах без шума, т.е. в таких каналах, где помехи отсутствуют, либо ими можно пренебречь. Основной задачей кодирования в таком канале является обеспечение максимальной скорости передачи информации, близкой к пропускной способности канала передачи (§3.4).

В случае, если все символы алфавита кодируемого сообщения независимы и их появление равновероятно, построение оптимального эффективного кода не представляет трудностей. Действительно, пусть Н(х) — энтропия исходного сообщения. Будем считать, что символы сообщения (х_i) равновероятны и объем алфавита исходного источника сообщений равен m. Следовательно, вероятность появления любого i-го символа данного сообщения (P(х_i)) будет одинакова, т.е.

, i=1,.., m,

а энтропия сообщения равна (Н(х)):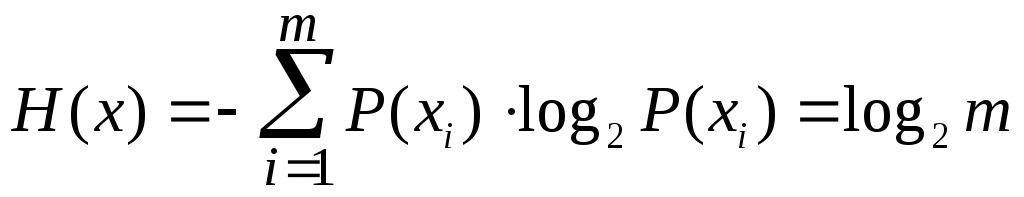

,

Если для кодирования используется числовой код по основанию k(объем алфавита элементов кодовых символов равен k), то энтропия элементов кодовых символов (Н₁), при условии, что элементы символов кода появляются равновероятно и взаимнонезависимо, определится из соотношения:

H₁ = log₂k .

Тогда длина эффективного равномерного кода, т.е. число элементов в кодовом символе (l_эфф.), может быть найдена из соотношения:

, (2.4)

где m = kⁿ.
2.4. Эффективное кодирование неравновероятных символов сообщений

В случае, если символы кодируемого сообщения неравновероятны, в общем виде правило получения оптимального эффективного кода неизвестно. Однако из общих соображений можно представить принципы его построения.

Очевидно, что эффективное кодирование будет оптимальным, если неравномерное распределение вероятностей появления символов алфавита источника сообщений с помощью определенным образом выбранного кода переводят в равновероятное распределение вероятностей появления независимых элементов кодовых символов. В этом случае среднее количество инфор­мации, приходящееся на один элемент символа кода, будет максимальным. Для определения вида кода, удовлетворяющего этому требованию, можно рассмот­реть «функцию стоимости» (цены передачи символов сообщения) в виде:

, (2.5)

где P(x_i) — вероятность появленияi-го символа алфавита исходного кодируемого сообщения;

m — объем алфавита;

W_i— стоимость передачи i-го символа алфавита, которая пропорциональна длине кодового слова.

Эффективный код должен минимизировать функцию Q. Если передача всех элементов символов кода имеет одинаковую стоимость, то стоимость кодового символа будет пропорциональна длине соответствующего кодового символа. Следовательно, в общем случае (при неравновероятных символах исходного сообщения) код должен быть неравномерным, поэтому построение эффективно­го кода должно основываться на следующих принципах:

1. 
   Длина кодового символа (n_i)должна быть обратно пропорциональна вероятности появления соответствующего символа исходного кодируемого сообщения (x_i);
   
2. 
   Начало более длинного кодового символа не должно совпадать с началом более короткого (для возможности разделения кодовых символов без применения разделительных знаков);
   
3. 
   В длинной последовательности элементы символов кода должны быть независимы и равновероятны.
   

Теоретическое обоснование возможности эффективного кодирования передаваемых по каналу сообщений обеспечивает теорема, доказанная К. Шенноном и которая носит название первая теорема Шеннона или основная теорема Шеннона о кодировании для каналов без помех. Эта теорема гласит, что если источник сообщений имеет энтропию Н бит/символ, а канал обладает пропускной способностью С бит/сек (пропускная способность характеризует максимально возможное значение скорости передачи информации), то всегда можно найти способ кодирования, который обеспечит передачу символов сообщения по каналу со средней скоростью

символ/сек,

где ε — сколь угодно малая величина.

Обратное утверждение говорит, что передача символов сообщения по каналу со средней скоростью V_ср. > Н невозможна и, следовательно,

символ/сек.

Эта теорема часто приводится в иной формулировке: сообщения источника сообщений с энтропией Н всегда можно закодировать последовательностями элементов кодовых символов с объемом алфавита m так, что среднее число элементов символов кода на один символ кодируемого сообщения (l _ср. ) будет сколь угодно близко к величине H/ log₂ m, но не менее ее.

Не вдаваясь в доказательство этой теоремы, отметим, что эта теорема показывает возможность наилучшего эффективного кодирования, при котором обеспечивается равновероятное и независимое поступление элементов символов кода, а следовательно, и максимальное количество переносимой каждым из них информации, равное log₂ m (бит/элемент) . К сожалению, теорема не указывает конкретного способа эффективного кодирования, она лишь говорит о том, что при выборе каждого элемента кодового символа необходимо чтобы он нес максимальное количество информации, а, следовательно, все элементы символов кода должны появляться с равными вероятностями и взаимнонезависимо.

Исходя из изложенных принципов, разработаны ряд алгоритмов эффективного кодирования как для взаимнонезависимых символов сообщения, так и для взаимнозависимых. Суть их состоит в том, что они сокращают среднюю длину кодовых символов путем присвоения кодовых символов минимальной длины символам исходного сообщения, которые встречаются наиболее часто.