динамика. Первый закон Ньютона. Инерциальные системы отсчета

• Название: Первый закон Ньютона. Инерциальные системы отсчета
• Дата: 30.09.2020
• Размер: 297.5 Kb.
• Имя файла: динамика.doc
• Тип: Закон; #140265

Динамикой называют раздел механики, в котором изучают различные виды механических движений с учетом взаимодействия тел между собой. Основы динамики составляют три закона Ньютона, являющиеся результатом обобщения наблюдений и опытов в области механических явлений, которые были известны еще до Ньютона и осуществлены самим Ньютоном.

Первый закон Ньютона. Инерциальные системы отсчета

К выводу о существовании явления инерции впервые пришел Галилей, а затем Ньютон. Этот вывод формулируется в виде первого закона Ньютона (закона инерции): существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на нею внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Следовательно, инерциальными являются такие системы отсчета, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем, а оси направлены на определенные "неподвижные" звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являются инерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющих глобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей, можно с достаточной точностью считать инерциальными. Инерциальными являются и системы отсчета, которые движутся равномерно и прямолинейно относительно какой-либо инерциальной системы отсчета (см. далее). Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности. Этот принцип был впоследствии развит А. Эйнштейном и является одним из постулатов специальной теории относительности.

Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета. В дальнейшем мы будем пользоваться только инерциальными системами (не упоминая об этом каждый раз).

Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными. К таким системам относится любая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета.

Сила. Второй закон Ньютона

Известно, что изменение скорости тела, т. е. появление ускорения, всегда происходит под действием на данное тело окружающих его тел. Для характеристики этих действий введено понятие силы.

Силой называют векторную величину, характеризующую такое действие на данное тело других тел (или полей), которое может вызвать ускорение и деформацию тела (здесь мы имеем в виду произвольное твердое тело, а не материальную точку).

Если на данное тело действует только одна сила, она обязательно вызывает и ускорение и деформацию тела. Если же на тело одновременно действуют несколько сил, то возможен и случай их компенсации (уравновешивания) и тело может не получать ускорения.

Поскольку сила способна вызывать и ускорение и деформацию тел, оба эти действия могут быть использованы для измерения силы и установления единицы ее измерения.

Динамометры и пружинные весы служат для измерения силы по производимой ею деформации. Использовав соотношение, существующее между силой, массой и ускорением, которое было впервые установлено Ньютоном и получило название второго закона Ньютона, можно определить силу по вызываемому ею ускорению. Наблюдения показывают, что если действовать одной и той же силой (например, силой упругости растянутой пружины) на тела различной массы, то модули ускорений, получаемых телами под действием этой силы, окажутся обратно пропорциональными массами этих тел, т. е.

a₁/a₂=m₂/m₁.


Из наблюдений следует также, что если на одно и то же тело поочередно действовать различными силами, то модули ускорений, получаемых телом под действием этих сил, окажутся пропорциональными модулям этих сил, т. е.

a₁/a₂=F₁/F₂.

Из последних двух формул видно, что а = F/m, следовательно, F=ma, или в векторной форме

F=ma.    

Эта формула выражает второй закон Ньютона, который формулируют так: сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этому телу силой.

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

Он играет большую роль в динамике системы материальных точек, как устанавливающий зависимость между действующими на эти точки внутренними

силами. При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ

Для решения многих задач динамики вместо непосредственного интегрирования дифференциальных уравнений движения оказывается более эффективным пользоваться так называемыми общими теоремами, которые являются следствием основного закона динамики.

Количество движения точки

Количеством движения материальной точки называется вектор, равный произведению массы точки на ее скорость .

Количество движения точки в физике часто называют импульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат равны:

, ,

Единицей измерения количества движения в СИ является –

Элементарный и полный импульс силы.

Действие силы на материальную точку в течении времени можно охарактеризовать элементарным импульсом силы .

Полный импульс силы за время , или импульс силы , определяется по формуле . (Полный интеграл за время от элементарного импульса).

В частном случае, если сила постоянна и по величине , и по направлению ( ), .

Проекции импульса силы на прямоугольные декартовы оси координат равны:



Единицей измерения импульса в СИ является –

Теорема об изменении количества движения точки.

Теорема. Производная по времени от количества движения точки равна действующей на точку силе.

Запишем основной закон динамики в виде . Так как масса постоянна, то внесем ее под знак производной.

Тогда , (*)

что и требовалось доказать.

В проекциях на координатные оси уравнение (*) можно представить в виде:



Теорема импульсов (в дифференциальной форме). Дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.

Умножим левую и правую части уравнения (*) на и получим

(**)

В проекциях на координатные оси получаем:

,

,

.

Теорема импульсов (в интегральной форме). Изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за этот же промежуток времени.

Интегрируя обе части уравнения (**) по времени в пределах от нуля до получаем:



В проекциях на координатные оси получаем:

,

,

Момент количества движения точки.

В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.

М оментом количеством движения материальной точки относительно некоторого центра О называется вектор, определяемый равенством

Момент количества движения точки называют также кинетическим моментом.

Момент количества движения относительно какой-либо оси , проходящий через центр О, равен проекции вектора количества движения на эту ось .

Если количество движения задано своими проекциями на оси координат и даны координаты точки в пространстве, то момент количества движения относительно начала координат вычисляется следующим образом:

Проекции момента количества движения на оси координат равны:







Единицей измерения количества движения в СИ является – .

Теорема об изменении момента количества движения точки.

Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.



Доказательство: Продифференцируем момент количества движения по времени

, , следовательно , (*)

что и требовалось доказать.

Теорема. Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси.

Для доказательства достаточно спроектировать векторное уравнение (*) на эту ось. Для оси это будет выглядеть так:

Следствия из теорем:

1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.

,

2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.

,

Работа силы. Мощность.

Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.

Э лементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.

. ,



Единицей измерения работы в СИ является –

При при

Частные случаи:





Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы.

Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.



Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.



Если сила задана своими проекциями ( ) на оси координат и элементарное перемещение задано своими проекциями ( ) на оси координат, то элементарная работа силы равна:

(аналитическое выражение элементарной работы).

Работа силы на любом конечном перемещении равна взятому вдоль этого перемещения интегралу от элементарной работы.



Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.

,

Мощность равна скалярному произведению силы на скорость.

Единицей измерения мощности в СИ является –

В технике за единицу силы принимается .

Пример 1. Работа силы тяжести.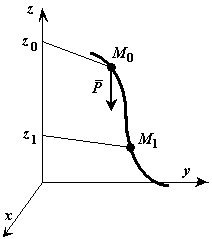

Пусть точка М, на которую действует сила тяжести Р, перемещается из положения в положение . Выберем оси координат так, чтобы ось была направлена вертикально вверх.

Тогда, , , и



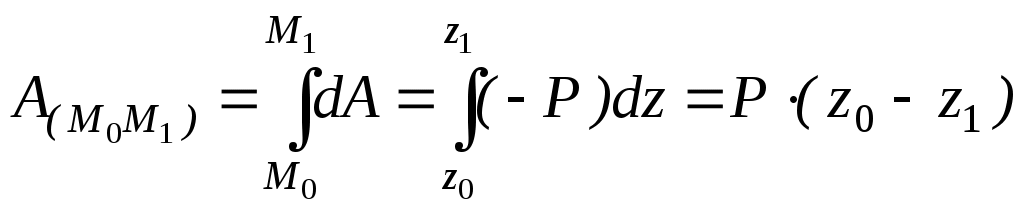Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.

Пример 2. Работа силы упругости.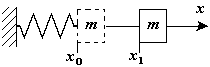

Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила) . Пусть точка М, на которую действует только сила упругости, перемещается из положения в положение . ( , ).



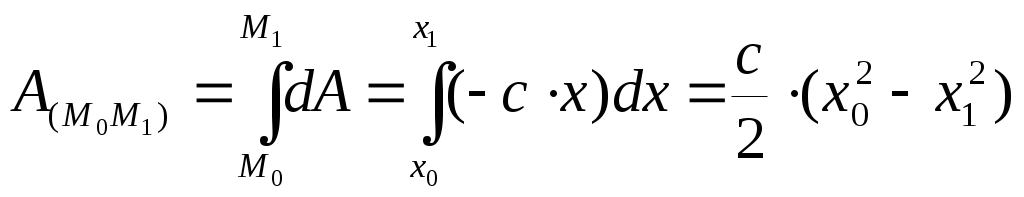Работа силы упругости равна половине произведения жесткости упругого элемента на разность квадратов начального и конечного удлинения (или сжатия) упругого элемента.

Работа силы упругости равна площади фигуры (трапеции) расположенной под кривой .

Пример 3. Работа и мощность пары сил.

П усть пара сил приложена к вращающемуся вокруг неподвижной оси телу. Элементарная работа пары сил равна . Полная работа пары сил равна

- угол поворота тела, - момент пары сил.

Мощность пары сил равна

Кинетическая энергия точки

Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.

Теорема об изменении кинетической энергии точки.

Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.



Доказательство: Основной закон динамики .

Умножим левую и правую части уравнения скалярно на справа, получаем . - элементарная работа.

- дифференциал от кинетической энергии.

, что и требовалось доказать.

Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.



Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.

Принцип Даламбера для материальной точки

Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:

,

- равнодействующая активных сил, - равнодействующая сил реакции связей.

Силой инерции материальной точки называют произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. .

Если использовать понятие силы инерции, то основной закон динамики принимает вид:

Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил.

Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.