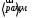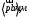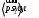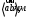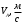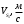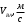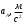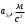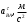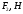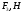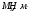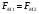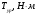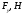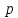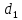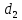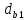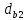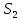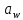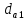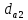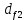Кинематический анализ и общее проектирование машинного привода от двигателя внутреннего сгорания». Курсовая по ТММ — копия. петербургский государственный университет путей сообщения императора александра i
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
 ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I» (ФГБОУ ВО ПГУПС) Факультет «Транспортные и энергетические системы» Кафедра «Наземные транспортно-технологические средства» Курсовая работа по дисциплине «Теория машин и механизмов» Вариант Выполнил студент: Группа: ПТМ Курс: Факультет: БФО Преподаватель: Санкт-Петербург 2023 ОглавлениеВведение 3 Исходные данные 4 2 Структурное исследование механизма 5 3 Кинематический анализ 8 3.1 Построение схемы механизма 8 3.2 Построение планов скоростей механизма 9 3.2 Построение планов ускорений механизма 11 4 Силовой расчет рычажного механизма 15 4.1 Определение сил и моментов, приложенных к механизму 15 4.2 Определение уравновешивающей силы методом Жуковского 16 5 Проектирование эвольвентного зацепления 18 Список литературы 21 Приложения 22 ВведениеОбъектом исследования является механизм двигателя внутреннего сгорания. Механизм двигателя внутреннего сгорания включает в себя различные механизмы, из которых исследованию подлежат – рычажный и зубчатый. Рычажный механизм служит для преобразования возвратно-поступательное перемещение поршня во вращательное движение кривошипа. От кривошипа вращательное движение передается через зубчатую передачу z1 и z2. В рычажных механизмах угловая скорость непостоянна и для более равномерного движения на валу кривошипа установлен маховик. В данной курсовой работе необходимо произвести: Провести структурный, геометрический, кинематический и силовой расчёт механизма и определить уравновешивающий момент 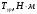 . .Выполнить кинематический расчёт редуктора. Определить размеры зубчатых колёс редуктора. Построить картину зубчатого эвольвентного зацепления. Исходные данные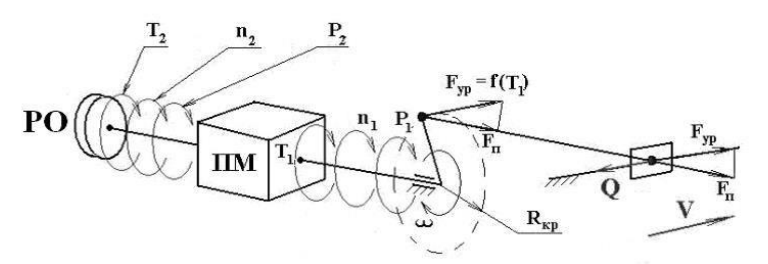 Рис.1.1. Схема механизма
2 Структурное исследование механизмаВыполним структурный анализ рычажного механизма, определим его подвижность и класс.  Рис. 2.1. Структурная схема рычажного механизма Проанализируем звенья механизма, а также вид совершаемого ими движения, кинематические пары, соединяющие эти звенья (рис. 2.1), все данные занесём в таблицы: Таблица 2.1 Звенья механизмов
Таблица 2.2 Кинематические пары механизмов
Т.к., данный механизм является плоским, то подвижность механизма определим по формуле Чебышева: 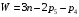 где  — число подвижных звеньев, в данном механизме их 3 (табл. 1.1); — число подвижных звеньев, в данном механизме их 3 (табл. 1.1);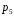 — число одноподвижных кинематических пар 5 класса, в данном механизме их 4 (табл. 2.2); — число одноподвижных кинематических пар 5 класса, в данном механизме их 4 (табл. 2.2); — количество двухподвижных пар 4 класса, в данном механизме их нет (табл. 1.2). — количество двухподвижных пар 4 класса, в данном механизме их нет (табл. 1.2). . .Схема любого плоского механизма может быть создана последовательным присоединением к ведущему звену и стойке кинематических цепей, которые не изменяют подвижность механизма. Разобьем данный рычажный механизм на структурные группы, т.е., на простейшие кинематические цепи с нулевой подвижностью относительно тех звеньев, с которыми входят в кинематические пары V кл. свободные элементы их звеньев, и не распадающиеся на более простые кинематические цепи с нулевой подвижностью. На рисунке 2.3 изображены структурные группы механизма. 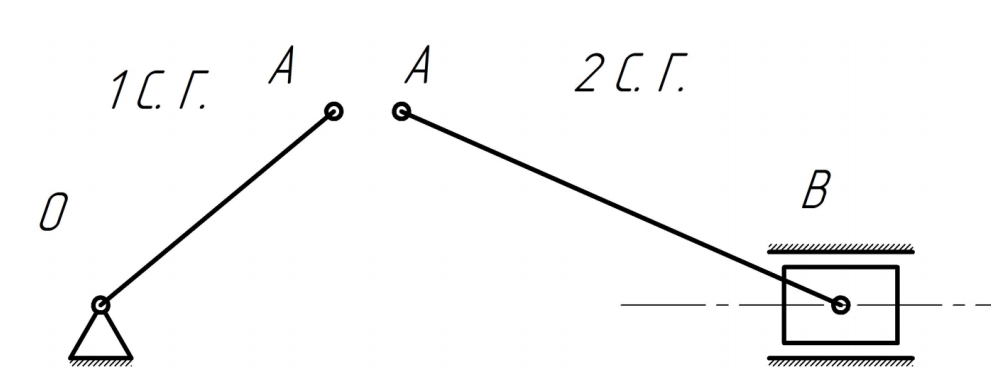 Рис. 2.2 Структурные группы механизма Запишем формулу строения механизма в порядке соединения: I(1,4)→II(2,3) Класс механизма определяется наивысшим классом входящих в него структурных объектов. Т.е., данный механизм является механизмом II класса. 3 Кинематический анализ3.1 Построение схемы механизмаПриняв на чертеже отрезок 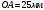 , находим масштаб механизма: , находим масштаб механизма: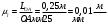 где 𝐿𝑂𝐴 — истинная длина звена в метрах, OA — изображение этого звена на чертеже в миллиметрах. Схема позволяет определить движение ведомых звеньев по заданному движению ведущих. Кинематические пары обозначают большими буквами латинского алфавита. Звенья обозначают арабскими цифрами, начиная с кривошипа. Планом механизма называется графическое изображение в масштабе кинематической схемы механизма, соответствующее определенному положению главного звена (в данном случае – кривошипа OA).  Рис 3.1 План положений механизма Для построения 8 положений звеньев механизма разделим траекторию, описываемую точкой А кривошипа, на 8 равных частей. В качестве нулевого принимаем то положение кривошипа, при котором точка В ползуна занимает крайнее верхнее положение. Из отмеченных на окружности точек А0, А1…А5 проводим дуги радиуса 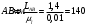 намечаем на линии движения ползуна B точки B0, B1…B7, и соединяем их соответствующим образом. намечаем на линии движения ползуна B точки B0, B1…B7, и соединяем их соответствующим образом.3.2 Построение планов скоростей механизмаОпределим частоту вращения кривошипа: 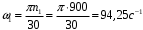 Определяем скорость точки А. 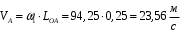 Примем длину вектора  , изображающего вектор скорости точки A, равной 50 мм. Тогда масштаб для плана скоростей: , изображающего вектор скорости точки A, равной 50 мм. Тогда масштаб для плана скоростей: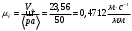 В векторной форме составим уравнение для скорости точки B: 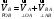 Под векторами указаны их направления. Далее, находим середину вектора 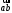 , изображающего скорость , изображающего скорость 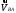 , и отмечаем точку , и отмечаем точку 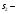 конец вектора конец вектора  , изображающего скорость центра тяжести шатуна , изображающего скорость центра тяжести шатуна 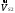 . Планы скоростей представлены на рис. 3.2. . Планы скоростей представлены на рис. 3.2.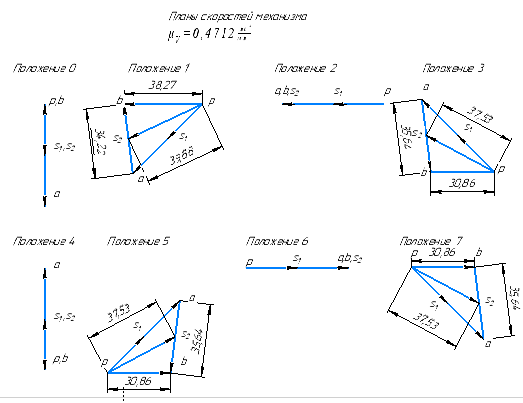 Рис. 3.2 Планы скоростей механизма Скорости нужных точек и звеньев для положения 5 находим по формулам: 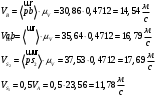 Угловая скорость звена 2: 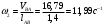 Построение планов скоростей заданных положений проводим аналогично. Результаты всех построений и расчетов представлены в табл. 3.1 и 3.2. Табл. 3.1 Отрезки с планов скоростей
Табл. 3.2 Значения точек скоростей точек механизма
Направление угловой скорости звена АВ определяется следующим образом. Переносим мысленно вектор bа с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А. 3.2 Построение планов ускорений механизмаПостроение плана ускорений рассмотрим для положения механизма №5 . Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А кривошипа будет иметь только нормальное ускорение, величина которого равна: 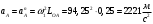 Ползун 3 совершает прямолинейное движение ,ускорение точки В будет равно 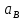 и направлено по ОВ. и направлено по ОВ.Векторное уравнение скорости точки В будет иметь вид: 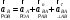 Под векторами указаны их направления. Для положения 5: 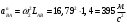 Вводим полюс плана ускорений 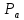 .Из полюса .Из полюса  откладываем вектор откладываем вектор 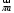 в выбранном масштабе и получаем точку «a» из этой точки откладываем вектор в выбранном масштабе и получаем точку «a» из этой точки откладываем вектор 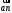 (направлен по АВ в сторону точки А). Из точки n проводим вектор (направлен по АВ в сторону точки А). Из точки n проводим вектор  (направлен перпендикулярно АВ). Из полюса (направлен перпендикулярно АВ). Из полюса  откладываем направление ускорения откладываем направление ускорения 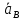 и точка пересечения векторов и точка пересечения векторов  и и 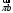 дает нам точку пересечения «b». Длина отрезка дает нам точку пересечения «b». Длина отрезка 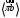 дает нам величину ускорения точки В, а длина отрезка дает нам величину ускорения точки В, а длина отрезка 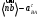 . Отмечаем на отрезке . Отмечаем на отрезке 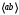 середину S2 и получаем ускорение центра тяжести звена 2. середину S2 и получаем ускорение центра тяжести звена 2.Примем длину вектора 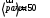 . Тогда, масштаб для плана ускорений: . Тогда, масштаб для плана ускорений: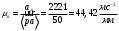 Рассчитаем 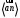 : :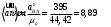 Ускорения нужных точек и звеньев находим по формулам: 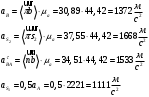 Угловое ускорение звена 2: 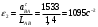 Направлена 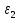 по по  из точки В. из точки В.Планы ускорений представлены на рисунке 3.3. 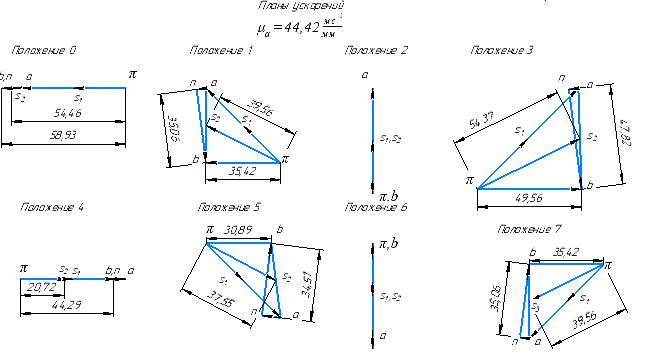 Рис. 3.3 Планы ускорений Для остальных положений все расчеты и построения ведутся аналогично. Результаты всех построений и расчетов сведены в таблицу: Таблица 3.1 — Значения ускорений в расчетных положениях
4 Силовой расчет рычажного механизма4.1 Определение сил и моментов, приложенных к механизмуПлан нагрузок механизма предусматривает нанесение на его схему векторов сил, действующих в его шарнирах и центрах масс, на основании которых в дальнейшем находится мгновенное значение уравновешивающей силы. При простейшем кинематическом анализе на план нагрузок наносятся вектора веса звеньев G, внешняя нагрузка Q, уравновешивающая сила FУР и инерционные нагрузки FИ. Вектора последних направляются противоположно ускорениям центров масс по плану ускорений. Планы нагрузок представлены в графической части курсовой работы. Центры тяжести звеньев (стержней)находятся на середины их длины. Центр тяжести ползуна совпадает с центров шарнира В. Вес звеньев определяется по формуле: 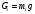 Где  – ускорения свободного падения. – ускорения свободного падения. Силы инерции звеньев вычисляются по формуле: 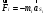 Где 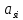 -ускорение центра масс i-ого звена. -ускорение центра масс i-ого звена.Знак «-» показывает, что силы инерции направлены противоположно ускорению центра масс звена. Моменты инерции звеньев относительно их оси вращения: 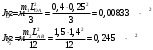 Вычислим силы инерции для 4 положений механизма (5,6,7,0): Табл. 4.1 — Силы инерции
4.2 Определение уравновешивающей силы методом ЖуковскогоСоотношение между силами, приложенными к механизму (включая и силы инерции), можно получить с помощью вспомогательного рычага Жуковского. Если какой-либо механизм под действием системы сил, приложенных к этому механизму, находится в равновесии, то повернутый на 90 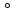 в сторону вращения уголовной скорости план скоростей, рассматриваемый как твердое тело, вращающегося вокруг полюса плана и нагруженное теми же силами, приложенными в соответствующих точках плана, также находится в равновесии. При этом, силы, приложенные к полюсу в сторону вращения уголовной скорости план скоростей, рассматриваемый как твердое тело, вращающегося вокруг полюса плана и нагруженное теми же силами, приложенными в соответствующих точках плана, также находится в равновесии. При этом, силы, приложенные к полюсу 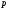 или пересекающие его не указываем, чтобы не загромождать рисунки. или пересекающие его не указываем, чтобы не загромождать рисунки.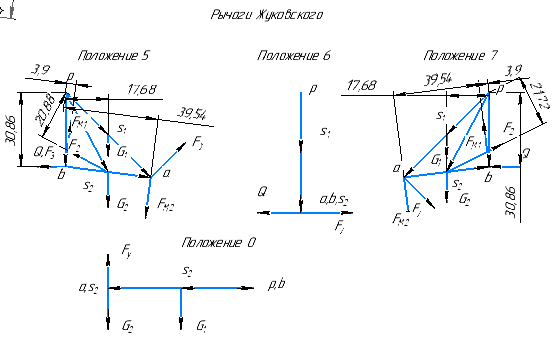 Рис. 4.1. Рычаги Н. Е. Жуковского. Раскладываем момент инерции звена 2 на пару сил: 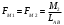 Табл. 4.2 Значение пары сил от момента инерции
Составим уравнения моментов сил относительно полюса 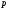 . .Положение 5: 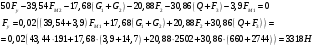 Положение 6: 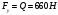 Положение 7: 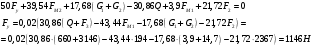 Положение 0:  Определяем уравновешивающий момент по формуле 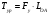 Все вычисления приводим в таблицу 4.4: Табл.4.4 Полученные результаты
Наибольшую нагрузку по модулю кривошип испытывает в положении 5, поэтому расчет редуктора производим по этому значению. 5 Проектирование эвольвентного зацепленияПо найденному максимальному значению уравновешивающей силы, приложенной к кривошипу, определяем вращающийся момент на входном валу привода: Мощность на валу кривошипа: 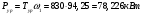 Определим мощность на валу РРО: 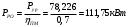 Передаточное отношение редуктора принимаем по рекомендациям для одноступенчатых прямозубых редукторов. Принимаем  . .Рассчитаем частоту вращения валов редуктора: 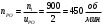 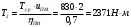 Рассчитываем межосевое расстояние:  Где 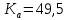 —коэффициент межосевого расстояния для цилиндрических зубчатых колес; —коэффициент межосевого расстояния для цилиндрических зубчатых колес;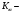 коэффициент ширины колес относительно опор; коэффициент ширины колес относительно опор; – передаточное число; – передаточное число;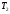 – вращающий момента на тихоходном валу редуктора; – вращающий момента на тихоходном валу редуктора; − допускаемое контактное напряжение колеса; − допускаемое контактное напряжение колеса; коэффициент неравномерности по длине зуба. коэффициент неравномерности по длине зуба.По ГОСТ 2185-66 выбираем ближайшее стандартное межосевое расстояние (ряд 1): Принимаем 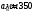 . .Определяем модуль зацепления: 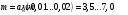 Значение модуля округляется до стандартного числа согласно ГОСТ 9563-60. Принимаем 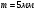 . .Определим суммарное количество зубьев шестерни и колеса: 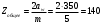 Примем  . .Число зубьев шестерни: 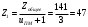 Число зубьев колеса: 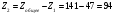 Уточнение передаточного числа: 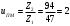 В каждом зубчатом колесе различают три окружности и, следовательно, соответствующие им диаметры: делительные диаметры шестерни и колеса: 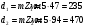 Диаметры окружностей вершин зубьев шестерни и колеса: 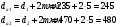 Диаметры окружностей впадин зубьев шестерни и колеса: 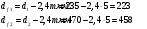 Диаметры основных окружностей: 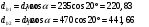 Толщина зуба по делительной окружности:  Расстояние между одноименными боковыми поверхностями двух смежных зубьев колеса называется шагом и рассчитывается по формуле: 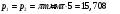 Вычислим значения геометрических параметров зубчатых колёс и занесём данные в таблицу: Уточним межосевое расстояние:  Табл. 5.1 Результаты расчета
Список литературы1. Артоболевский И.И. Теория механизмов и машин М., Наука. 1975. 2. Турбин Б.И., Карлин В.Д. Теория механизмов и машин. М.. Машиностроение. 1980. Дополнительная 3. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. М., Наука. 1975. 4. Баранов Г.Г. Курс теории механизмов и машин М. Машиностроение, 1990. ПриложенияФайлы построений: Зубчатый механизм.cdw – Файл построения эвольвентного зацепления; Зубчатый механизм.pdf – Сохранённая в формате ПДФ копия построения эвольвентного зацепления; Рычажный механизм.cdw – Файл расчётов рычажного механизма; Рычажный механизм.pdf – Сохранённая в формате ПДФ копия расчётов рычажного механизма. |