Петербургский государственный университет путей сообщения
 Скачать 1.17 Mb.
|
|
Федеральное агентство железнодорожного транспорта Государственное образовательное учреждение высшего профессионального образования ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ Кафедра физики ОБРАБОТКА РЕЗУЛЬТАТОВ ЛАБОРАТОРНОГОФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА(Учебное пособие для студентов всех форм обучения)Громова Е.С. Панюшкин А.В. Бодунов Е.Н. CАНКТ–ПЕТЕРБУРГ 2008 ВВЕДЕНИЕОсновная задача всякого физического эксперимента, в том числе и лабораторного, состоит в измерении физических величин. Измерить какую-либо физическую величину – значит сравнить ее с другой однородной физической величиной, условно принятой за единицу измерения. В результате каждого отдельного измерения (оно называется наблюдением) получают числовое значение измеряемой величины. Измерения принципиально не могут быть абсолютно точными. Никакие измерения не дают возможности получить истинное значение измеряемой величины, что объясняется как принципиально ограниченной точностью приборов, так и природой самих измеряемых объектов. Всегда имеется некоторая неопределенность в значении измеряемой величины. Эта неопределенность характеризуется погрешностью – отклонением измеренного значения величины от ее истинного значения. Многократно измеряя любую физическую величину, можно, вообще говоря, получить какие угодно результаты. Например, измеряя длину некоторого тела, получили значения 171, 172, 169, 173, 170, 169, 171 см, а также 170 мм и 169 дм. Результаты двух последних измерений могут быть и ошибочными, являясь, например, следствием небрежного ведения записей. Однако, их наличие подчеркивает то обстоятельство, что принципиально и результат измерений, и его погрешность могут быть любыми, и, следовательно, оценивать точность измерения указанием результата и его погрешности, неверно – они могут принимать любые значения. Вместе с тем из анализа вышеприведенного ряда результатов видно, что большие по величине погрешности (соответствующие, по-видимому, двум последним результатам) маловероятны. Отсюда следует, что для правильной характеристики точности результата необходимо указывать не только величину погрешности, но и соответствующее ей значение вероятности. Таким образом, при выполнении измерений и обработке их результатов каждый экспериментатор должен иметь в виду следующие обстоятельства. 1) Всякое измерение должно по возможности быть проверено путем многократного повторения. 2) При измерении может быть получен лишь приближенный результат. 3) Степень приближенности результата должна быть задана величиной погрешности. 4) Степень доверия к найденным границам погрешности выражается значением ее вероятности. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ Абсолютная погрешность   ого наблюдения какой–либо физической величины определяется разностью (1)где  – значение физической величины, найденное в ом наблюдении,  – истинное значение измеряемой величины, как правило, неизвестное. Абсолютная погрешность выражается в тех же единицах, что и сама измеряемая величина. Значения абсолютной погрешности могут быть как положительными, так и отрицательными. Для характеристики точности измерений недостаточно оперировать только значением абсолютной погрешности. Важно знать, какую долю составляет эта погрешность от значения измеряемой величины. Отношение  (2)называется относительной погрешностью ого наблюдения какой–либо физической величины и выражается в долях или процентах.Заметим, что выражения (1) и (2) определяют истинные значения абсолютной и относительной ошибок, которые не могут быть определены также как и истинное значение самой измеряемой величины. На практике вместо истинного значения величины используют ее наилучшее приближение.ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ И ДОВЕРИТЕЛЬНАЯ ПОГРЕШНОСТЬ При обработке результатов измерений любой физической величины возникают две задачи. Первая состоит в нахождении по набору данных наилучшей оценки измеряемой величины  , которую с наибольшим основанием можно принять за приближенное значение величины . Вторая – в определении точности полученного результата.Результат измерения физической величины представляют в виде   Приведенная запись означает, что существует определенная степень уверенности в том, что значение измеряемой величины находится в пределах рассчитанного по результатам наблюдений интервала  , называемого доверительным. Величина  называется доверительной погрешностью.Указание значения доверительной вероятности   означает, что при проведении большого числа наблюдений в  случаев результаты наблюдений измеряемой физической величины, выполненные с одинаковой тщательностью и одними и теми же измерительными приборами, попадут внутрь доверительного интервала.Значения доверительной погрешности и доверительной вероятности однозначно связаны друг с другом, а именно: чем больше погрешность, тем больше вероятность того, что результат измерений находится в указанных пределах, и наоборот. ВИДЫ ПОГРЕШНОСТЕЙ По характеру, происхождению, а также по способам оценки и исключения влияния на результат измерений погрешности делят на три основные группы: случайные, систематические и грубые (промахи). Систематические и грубые погрешности определяются факторами, чуждыми условиям и проведению эксперимента. Погрешности такого рода могут быть исключены путем тщательных проверок. Систематические погрешности связаны с ограниченной точностью прибора и метода измерений, а также округлением при считывании значения со шкалы. Когда причины, вызывающие эти погрешности, известны, их можно исключить, уточняя метод измерения и вводя поправки к показаниям приборов. Систематические погрешности не уменьшаются с увеличением числа измерений. Грубые погрешности (промахи) обычно связаны с отсутствием достаточной квалификации экспериментатора, неправильным отсчетом по прибору, неправильной записью результата наблюдения, невнимательностью и т.п. Обычно грубые погрешности хорошо заметны, т.к. при многократно проделанных измерениях соответствующие промахам результаты резко отличаются от остальных. Такие погрешности могут возникать в результате неустойчивой работы установки или отдельного прибора. Они могут быть устранены путем повторных измерений или снятием показаний другим экспериментатором. Случайные погрешности обусловливаются большим количеством трудноучитываемых факторов, влияющих как на измерительные устройства, исследуемый физический объект или процесс, так и на самого экспериментатора. Такими факторами могут быть, например, колебания температуры элементов установки, напряженностей электрического и магнитного полей, движение воздуха, вибрация зданий и приборов, трение в движущихся элементах, погрешности при отсчете делений шкалы и т.п. Исключить случайные погрешности отдельных измерений невозможно, но величину таких погрешностей можно оценить, проводя повторные (многократные) измерения. Оценка величины случайных погрешностей производится с помощью аппарата математической статистики и теории вероятностей. ПРЯМЫЕ И КОСВЕННЫЕ ИЗМЕРЕНИЯ По способу получения результата измерения делятся на прямые и косвенные. Если значение физической величины находят непосредственным отсчетом по шкале прибора, то такие измерения называются прямыми (измерения давления барометром, температуры – термометром, времени – секундомером, длины – штангенциркулем или линейкой, силы тока – амперметром и т.п.). Эти измерения могут быть однократными и многократными. Многократное измерение – повторение экспериментельной операции, в результате которой получается одно из значений измеряемой величины , называемых результатами наблюдений. Совокупность результатов наблюдений подлежит совместной обработке для получения результата измерения.Часто прямое измерение физической величины оказывается невозможным или слишком трудоемким. При косвенных измерениях результат определяется по формулам на основе результатов прямых измерений других величин (например, определение электрического cопротивления образца по измеренным силе тока и напряжению). Одну и ту же величину часто можно найти путем как прямых, так и косвенных измерений. Например, скорость автомобиля может быть определена по спидометру (прямое измерение) или найдена делением пройденного пути на время движения (косвенное измерение). При косвенных измерениях погрешность искомой физической величины накапливается из погрешностей прямых измерений величин, входящих в расчетную формулу. ПОГРЕШНОСТИ МНОГОКРАТНЫХ ПРЯМЫХ ИЗМЕРЕНИЙ(случайные погрешности) Пусть изучается физическая величина  и многократными измерениями получены  результатов наблюдений ,причем все измерения выполнены одним и тем же методом и с одинаковой степенью тщательности. Этот ряд значений величины называется выборкой. Предположим, что на результат измерений оказывают действие только случайные (неконтролируемые) факторы, а промахи и систематические ошибки отсутствуют. Задача экспериментатора состоит в том, чтобы найти наилучшую оценку и доверительную погрешность результата измерений для заданного значения доверительной вероятности. (При обработке экспериментальных результатов можно поступать и по–другому: произвольно задавать значение доверительной погрешности и вычислять соответствующее ей значение вероятности). Указанная задача строго решается с помощью теории вероятностей и математической статистики. В большинстве случаев случайные ошибки подчиняются установленному Гауссом нормальному закону распределения, вид которого может быть получен на основании следующих предположений: 1) величина случайной погрешности может иметь любое значение; 2) вероятность появления погрешности снижается с ростом ее величины – большие погрешности маловероятны; 3) погрешности, равные по величине, но разные по знаку, встречаются одинаково часто – равные по модулю погрешности равновероятны. Выведенный на основе указанных предположений закон нормального распределения случайных величин (распределение Гаусса) выражается формулой 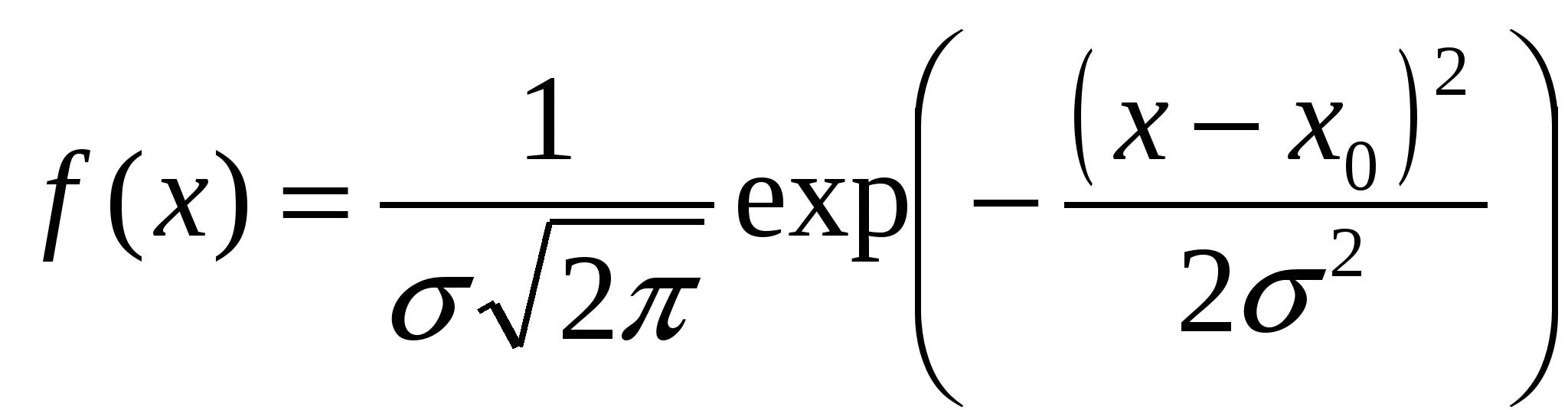 , (3)где – числовое значение определяемой величины ,  и  – параметры распределения;  – плотность вероятности (вероятность того, что значение принадлежит некоторому единичному интервалу значений), так что функция  определяет вероятность попадания значения в интервал от до  . Параметр , соответствующий максимуму плотности вероятности , называется математическим ожиданием случайной величины . Параметр называется средним квадратическим отклонением величины от ее математического ожидания и характеризует меру ее разброса относительно . Очевидно, что т.е. вероятность того, что случайная величина 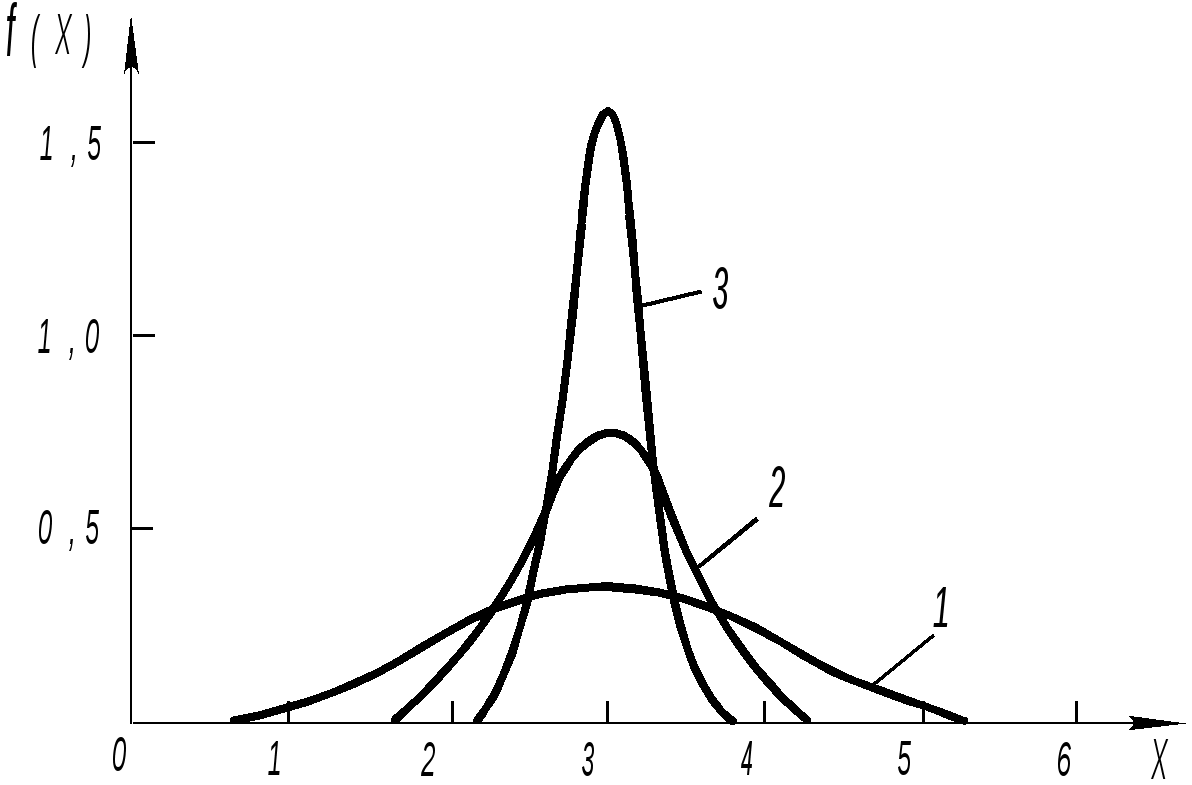вообще имеет какое–то значение, равна единице. Поскольку максимальное значение плотность вероятности принимает при  , то величину часто считают приблизительно равной истинному значению измеряемой величины. На рис.  представлен график этой функции. Из вышесказанного ясно, что площадь заштрихованной фигуры численно равна вероятности, с которой любой отсчет попадает в интервал от до  .Рис.1. Нормальное (гауссово) распределение (1 – , 2 – /2, 3 – /4) . Из теории следует, что наилучшей оценкой истинного значения  измеряемой случайной величины является среднее арифметическое (выборочное среднее) значение . (4)Заметим также, что с увеличением значения увеличивается разброс отсчетов, т.е. точность измерений понижается. В условиях реального эксперимента точное значение , как правило, неизвестно. По многократным измерениям  можно получить приближенную оценку этого параметра в виде среднеквадратичной погрешности  отдельного результата измерения , (5)которая характеризует ошибку каждого отдельного измерения и при неограниченном увеличении числа наблюдений (  ) стремится к истинной среднеквадратичной ошибке .Если произвести несколько серий многократных измерений, т.е. получить несколько выборок и для каждой вычислить выборочное среднее, то получим выборку для новой случайной величины  , которая также распределена нормально с математическим ожиданием  . Однако параметр  меньше, чем  : .Это означает, что выборочное среднее имеет приблизительно в  меньший разброс, чем единичное измерение . Поэтому для оценки лучше использовать выборочное среднее  и среднеквадратичную погрешность  среднего арифметического результата измерения, которая вычисляется по формуле , (6)В выражениях (5) и (6) обозначение среднеквадратичной ошибки заменено на обозначение  , чтобы подчеркнуть, что величины и  вычисляются на основе ограниченного числа наблюдений, т.е. являются эмпирическими оценками теоретических параметров  и .При проведении реальных технических измерений число отдельных измерений, как правило, невелико и лежит в пределах от  до  . В такой ситуации рассмотренный метод приводит к существенному искажению результатов. В теории погрешностей при малом числе измерений применяют специальный метод вычисления доверительного интервала, основанный на распределении Стьюдента. В 1908 г. английский математик У. Госсет (псевдоним ’’Стьюдент’’) доказал, что указанными соотношениями можно пользоваться и при небольшом числе наблюдений (  ), следует только на конечной стадии ввести в расчет специальный коэффициент, величина которого зависит от числа наблюдений и требуемого значения доверительной вероятности , – так называемый коэффициент Стьюдента  .Таблица 1 Коэффициенты Стьюдента .
Выполнение и обработку результатов прямых многократных измерений рекомендуется производить в следующем порядке. 1. Прямыми измерениями получить ряд значений измеряемой величины.2. Вычислить среднеарифметическое значение результата измерений  . 3. Вычислить отклонения отдельных результатов наблюдений от среднего  4. Вычислить значения  и сумму  .5. Для данных значений числа измерений и доверительной вероятности найти по таблице коэффициент Стьюдента  и вычислить случайную погрешность . (7)6. Округлив погрешность и предварительный результат, записать окончательный результат измерений в виде  Пример. Обработка результатов прямых многократных измерений диметра  некоторого вала штангенциркулем. Получены 6 значений  , которые внесены во 2–й столбец таблицы 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
