Лабораторная работа. Поддержание заданного уровня жидкости в резервуаре
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Отчёт по лабораторной работе
Цель работы: изучение процесса поддержания заданного уровня жидкости в накопительном баке, а также его характеристик Задачи: Исследовать зависимость величины установившегося значения уровня воды при постоянных значениях входного и выходного расхода от величины начального уровня воды. Установить значение диаметра бака равным 0,5 м. Регулировками значений входного расхода и выходного сечения трубопровода добиться стационарного значения уровня воды в диапазоне (7- 8) м Изменять начальный уровень в диапазоне от 0 до 9 м. Определить величину установившегося уровня и время достижения стационарного состояния. Повторить измерения для стационарного уровня в диапазоне (1-3) м. Результаты измерений занести в таблицу. По данным измерений построить соответствующие графические зависимости. Все графические зависимости отобразить на одном графике.. Исследовать зависимость значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода. Измерения провести для двух значений диаметра резервуара ( 0,5 м и 1,0 м) и трех значений сечения трубопровода (20, 40 и 80 отн.ед). Установить значение диаметра резервуара равным 0,5 м и сечение отводящего трубопровода равным 0,2 отн. ед. Пошагово изменять значение расхода поступающей воды от минимального значения до максимально возможного (в пределах срабатывания блокировок). Всего не менее 7 шагов. При каждом значении расхода измерять значение установившегося уровня и время выхода на стационарный режим. Повторить измерения для других значений сечения трубопровода и диаметра резервуара. Результаты измерений занести в таблицу. По данным измерений построить графики. По данным измерений и используя теоретические материалы, содержащиеся в данной лабораторной работе, определить величину гидравлического сопротивления трубопровода (коэффициент сужения струи положит равным = 0,75). Провести анализ полученных результатов и выявить закономерности, обнаруженные при исследовании процесса наполнения резервуара с водой. Объяснить обнаруженные закономерности. Убедиться, что увеличение периода сглаживания приводит к уменьшению флуктуация измеряемой величины, но с другой стороны может приводить к существенным ошибкам при достаточно быстром изменении условий. Например, в процессе заполнения резервуара и достижения стационарного режима. Для этого сравнить изменение во времени действительного значения уровня воды и значение, полученное в результате усреднения с использованием алгоритма «скользящее» среднее при нескольких значениях количества шагов усреднения. Например, N = 3, N=10, N = 30, N=100. Дать описание результатов наблюдений и объяснить наблюдаемую закономерность. Ход работы: Установим значение диаметра резервуара 0,5м. Регулируем значение входного расхода и выходного сечения так, чтобы стационарное значение уровня воды было в диапазоне 7-8 м. Опытным будем было выяснено, что значение уровня воды будет находиться в диапазоне 7-8м при входном расходе примерно 1,42 отн.ед. и при значении выходного сечения 50 отн.ед. Будем менять начальный уровень от 0 до 9 метров и определим для каждого значения начального уровня время достижения стационарного состояния и величину установившегося уровня воды в резервуаре. Данные занесем в таблицу 1. При этом стоит учесть, что данные для таблицы определяются при помощи осциллограммы вручную, так что значения могут быть отличны от реальных значений стационарного состояния. Таблица 1 – зависимость длительности достижения стационарного уровня от начального уровня воды в резервуаре при стационарном значении уровня воды в диапазоне 7-8 м
Теперь регулируем значение входного расхода и выходного сечения так, чтобы стационарное значение уровня воды было в диапазоне 1-3 м. Установим расход поступающей воды 1,9 отн.ед., а выходное сечение 80 отн.ед. Тогда стационарное значение уровня воды будет примерно равно 1,9. Так же будем менять начальный уровень воды от 0 до 9 м. Данные занесем в таблицу 2. При этом стоит учесть, что данные для таблицы определяются при помощи осциллограммы вручную, так что значения могут быть отличны от реальных значений стационарного состояния. Таблица 2 – зависимость длительности достижения стационарного уровня от начального уровня воды в резервуаре при стационарном значении уровня воды в диапазоне 1-3 м
Построим в одной плоскости графики по данным таблицы 1 и таблицы 2. Они представлены на рис 1.1  Рис 1.1 – график зависимости длительности достижения стационарного уровня от начального уровня воды в резервуаре при стационарном значении уровня воды в различных диапазонах Рассмотрев графики, мы можем сделать вывод, что чем сильнее начальный уровень воды приближен к стационарному значению, тем быстрее уровень жидкости приближается к стационарному значению. При этом чем сильнее начальный уровень будет отличаться от стационарного значения, тем дольше будет идти процесс выравнивания. Установим диаметр резервуара 0,5 м, сечение отводящего трубопровода 0,56 отн.ед. (сечение 0,2 поставить не удается). Будем менять значение расхода поступающей воды от минимально возможного, до максимального. При каждом значении будем записывать значение установившегося уровня и время выхода на стационарный режим. Результаты представлены в таблице 3. Таблица 3 – зависимость значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода 0,56 отн.ед. и диаметре резервуара 0,5 м
Можем заметить, что при сечении 0,56 отн.ед. установленный уровень не попадает в диапазон от 1 до 9 м. Могу предположить, что это происходит из-за того, что при небольшом значении сечения трубопровода достаточно быстро происходит переполнение бака (уровень воды быстро поднимается и полностью заполняет бак). При этом чем больше будет расход поступающей воды, тем быстрее будет происходить переполнение бака Установим сечение 20 отн.ед. Так же будем менять значение расхода поступающей воды от минимально возможного, до максимального. При каждом значении будем записывать значение установившегося уровня и время выхода на стационарный режим. Результаты представлены в таблице 4. Таблица 4 – зависимость значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода 20 отн.ед. и диаметре резервуара 0.5 м
Выполним те же действия для сечения 40 отн.ед. Результаты представлены в таблице 5 Таблица 5 – зависимость значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода 40 отн.ед. и диаметре резервуара 0.5 м
Повторим все то же самое для сечения 80 отн.ед. результаты представлены в таблице 6 Таблица 6 – зависимость значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода 80 отн.ед. и диаметре резервуара 0.5 м
По данным таблиц 3, 4, 5 и 6 в одной плоскости построим графики зависимости значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода и диаметре резервуара 0,5 м. Графики представлены на рис 2.1  Рис 2.1 – графики зависимости значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода и диаметре резервуара 0,5 м. Составим график зависимости времени выхода на стационарный режим от значения установившегося уровня. Он представлен на рис 2.2  Рис 2.2 – график зависимости времени выхода на стационарный режим от значения установившегося уровня при диаметре резервуара 0,5м Увеличим диаметр резервуара до 1 м и выполним те же самые действия, что и для резервуара диаметром 0,5 м. Построим графики зависимости значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода и диаметре резервуара 1 м. Графики представлены на рис 2.2  Рис 2.3 – график зависимости значения стационарного уровня (в диапазоне от 1,0 м до 9,0 м) от расхода поступающей воды при постоянном значении сечении выходного трубопровода и диаметре резервуара 1 м. Составим график зависимости времени выхода на стационарный режим от значения установившегося уровня при диаметре резервуара 1м. он представлен на рис 2.4  Рис 2.4 – график зависимости времени выхода на стационарный режим от значения установившегося уровня при диаметре резервуара 1м. Рассмотрев графики, мы можем заметить, что они являются идентичными. При увеличении диаметра резервуара изменилось только время выхода на стационарный режим (оно увеличилось, так как произошло увеличение объема резервуара с водой). Это означает, что диаметр резервуара не влияет на значение стационарного уровня от расхода поступающей воды при постоянном сечении выходного трубопровода. Он влияет только на время выхода на стационарный режим. Рассчитаем величину гидравлического сопротивления трубопровода для трубы сечение 20 отн.ед с расходом поступающей воды, отн. ед. равного 0.12, диаметр резервуара 0,5 м (для статистического режима): Из формулы расхода вытекающей воды, связанный с уровнем воды в резервуаре, выведем формулу для нахождения гидравлического сопротивления трубопровода: 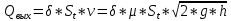 , (1) , (1) Где Qвых – объем воды, вытекающей из резервуара в единицу времени, т.е. объемный расход вытекающей воды; St – площадь проходного сечения трубопровода (или регулирующего вентиля);  - гидравлического сопротивления трубопровода; - гидравлического сопротивления трубопровода; - скорость течения жидкости (газа) в данном сечении трубопровода; - скорость течения жидкости (газа) в данном сечении трубопровода;g – ускорение свободного падения [м/с2]; h – высота столба жидкости относительно некоторого опорного уровня, [м];  - коэффициент сужения струи; - коэффициент сужения струи;Выразим гидравлическое сопротивление трубопровода из формулы (1):  , (2) , (2)Найдем  из формулы (1): из формулы (1): = 0,75 (по условию)  = 0,12 куб.м\мин. (из результатов расчета программы) = 0,12 куб.м\мин. (из результатов расчета программы) , (3) , (3)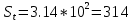   Найдем гидравлическое сопротивление трубопровода: h=1,66 м  = = 4. Установим начальный уровень воды в резервуаре 1м, диаметр резервуара 0,5м, расход поступающей воды 0,5 отн.ед. и выходное сечение 40 отн.ед. Будем менять скользящее среднее для того, чтобы убедиться, что увеличение периода сглаживания приводит к уменьшению флуктуации (любое случайное отклонение какой-либо величины) Установим 3 шага усреднения. Осциллограмма представлена на рис 4.1. Сравнение полученных результатов произведем непосредственно после того, как проведем все эксперименты  Рис 4.1 – осциллограмма процесса при среднем скользящем 3 шага Теперь поменяем количество шагов на 10. Остальные значения оставим неизменными. Осциллограмма представлена на рис 4.2  Рис 4.2 – осциллограмма процесса при среднем скользящем в 10 шагов Поменяем количество шагов на 30. Остальные значения оставим неизменными. Осциллограмма представлена на рис 4.3  Рис 4.3 – осциллограмма процесса при среднем скользящем в 30 шагов Поменяем количество шагов на 100. Остальные значения оставим неизменными. Осциллограмма представлена на рис 4.4  Рис 4.4 – осциллограмма процесса при среднем скользящем в 100 шагов Сравнив 4 осциллограммы, мы можем заметить, что чем больше мы ставим количество шагов, тем большее отклонение от уровня воды в баке будет иметь скользящее среднее в самом начале. Это может означать, что увеличение периода сглаживания может приводить к существенным ошибкам при достаточно быстром изменении условий Череповец 2020 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
