Понятие вектора
 Скачать 191.43 Kb. Скачать 191.43 Kb.
|
|
Понятие вектора. Линейные операции над векторами Понятие вектора. При изучении различных разделов физики, механики и технических наук встречаются величины, которые полностью определяются заданием их числовых значений. Такие величины называютсяскалярнымиили, короче,скалярами . Скалярными величинами, например, являются длина, площадь, объем, масса, температура тела и др. Помимо скалярных величин, в различных задачах встречаются величины, для определения которых, кроме числового значения, необходимо знать также их направление. Такие величины называютсявекторными. Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на нее сила. Векторные величины используются, например, и в климатологии. Рассмотрим простой пример из климатологии. Если мы скажем, что ветер дует со скоростью 10 м/с, то тем самым введем скалярную величину скорости ветра, но если мы скажем, что дует северный ветер со скоростью 10 м/с, то в этом случае скорость ветра будет уже векторной величиной. Векторные величины изображаются с помощью векторов. Векторомназывается направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая - за конец. ЕслиА - начало вектора иВ - его конец, то вектор обозначается символом Длина вектора Вектор называется нулевым(обозначается  Рис.24  Рис.25 Векторы Два вектора В этом случае пишут: Пример. Рассмотрим квадрат (рис. 25). На основании определения равенства векторов можем написать Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. Вектор, противоположный вектору 2. Линейные операции над векторами. Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. 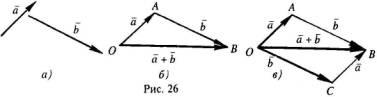 Определение. Пусть Отложим от точки О векторы Действительно, каждый из векторов Понятие суммы векторов, введенное для двух слагаемых векторов, можно обобщить на случай любого конечного числа слагаемых векторов. Пусть, например, даны три вектора Из рис. 27, б видно, что тот же вектор 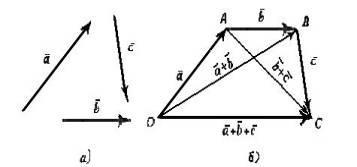 Рис.27 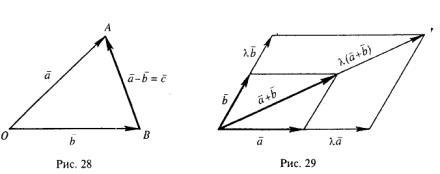 ( т.е. сумма векторов обладает сочетательнымсвойством. Поэтому сумму трех векторов Итак, сумму трех векторов можно получить следующим образом. Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго; к концу второго - начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов. Подобным же образом строится сумма любого конечного числа векторов. Если при сложении нескольких векторов конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нулевому вектору. Очевидно, что для любого вектора имеет место равенство Определение. Разностью Из определения суммы двух векторов вытекает правило построения вектора-разности (рис. 28). Откладываем векторы концы уменьшаемого вектора Определение. Произведением Так, западный ветер можно представить как отрицательный восточный ветер. Очевидно, что Пусть дан вектор т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует Очевидно, что и, обратно, из коллинеарности векторов Таким образом, два вектора Легко убедиться, что умножение вектора на число обладает +Справедливость, например, равенства (1) при Ранг матрицы и его свойства. Алгоритм вычисления ранга матрицы Ранг матрицы представляет собой важную числовую характеристику. Наиболее характерной задачей, требующей нахождения ранга матрицы, является проверка совместности системы линейных алгебраических уравнений. В этой статье мы дадим понятие ранга матрицы и рассмотрим методы его нахождения. Для лучшего усвоения материала подробно разберем решения нескольких примеров. Прежде чем озвучить определение ранга матрицы, следует хорошо разобраться с понятием минора, а нахождение миноров матрицы подразумевает умение вычисления определителя. Так что рекомендуем при необходимости вспомнить теорию статьи методы нахождения определителя матрицы, свойства определителя. Возьмем матрицу А порядка Определение. Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка Другими словами, если в матрице А вычеркнуть (p–k) строк и (n–k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы есть минор порядка k матрицы А. Разберемся с определением минора матрицы на примере. Рассмотрим матрицу 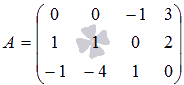 . .Запишем несколько миноров первого порядка этой матрицы. К примеру, если мы выберем третью строку и второй столбец матрицы А, то нашему выбору соответствует минор первого порядка Проиллюстрируем процедуру получения рассмотренных миноров первого порядка 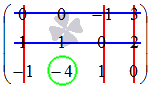 и и 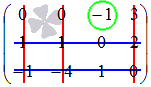 . .Таким образом, минорами первого порядка матрицы являются сами элементы матрицы. Покажем несколько миноров второго порядка. Выбираем две строки и два столбца. К примеру, возьмем первую и вторую строки и третий и четвертый столбец. При таком выборе имеем минор второго порядка 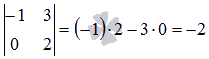 . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов. . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов.Другим минором второго порядка матрицы А является 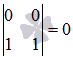 . .Проиллюстрируем построение этих миноров второго порядка 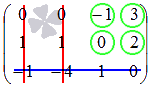 и и 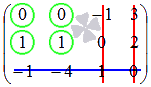 . .Аналогично могут быть найдены миноры третьего порядка матрицы А. Так как в матрице А всего три строки, то выбираем их все. Если к этим строкам выбрать три первых столбца, то получим минор третьего порядка  Он также может быть построен вычеркиванием последнего столбца матрицы А. Другим минором третьего порядка является  получающийся вычеркиванием третьего столбца матрицы А. Вот рисунок, показывающий построение этих миноров третьего порядка  и и  . .Для данной матрицы А миноров порядка выше третьего не существует, так как Сколько же существует миноров k-ого порядка матрицы А порядка Число миноров порядка k может быть вычислено как 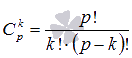 и и 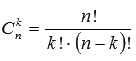 - число сочетаний из p по k и из n по k соответственно. - число сочетаний из p по k и из n по k соответственно.Как же построить все миноры порядка k матрицы А порядка p на n? Нам потребуется множество номеров строк матрицы Разберем на примере. Пример. Найдите все миноры второго порядка матрицы 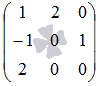 . .Решение. Так как порядок исходной матрицы равен 3 на 3, то всего миноров второго порядка будет 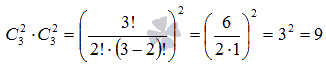 . .Запишем все сочетания из 3 по 2 номеров строк матрицы А: 1, 2; 1, 3 и 2, 3. Все сочетания из 3 по 2 номеров столбцов есть 1, 2; 1, 3 и 2, 3. Возьмем первую и вторую строки матрицы А. Выбрав к этим строкам первый и второй столбцы, первый и третий столбцы, второй и третий столбцы, получим соответственно миноры  Для первой и третьей строк при аналогичном выборе столбцов имеем  Осталось ко второй и третьей строкам добавить первый и второй, первый и третий, второй и третий столбцы:  Итак, все девять миноров второго порядка матрицы А найдены. Сейчас можно переходить к определению ранга матрицы. Определение. Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Ранг матрицы А обозначают как Rank(A). Можно также встретить обозначения Rg(A) или Rang(A). Из определений ранга матрицы и минора матрицы можно заключить, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы не меньше единицы. № 4.  Решим методом Гаусса. Для этого составим расширенную матрицу и приведем ее к ступенчатому виду путем умножения элементов строки на числа и сложения строк.    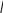   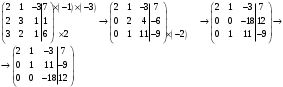 Система совместна и имеет единственное решение т.к. ранг расширенной матрицы равен рангу матрицы из коэффициентов и равен количеству неизвестных 3. Составим соответствующую систему уравнений и решим ее. 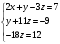  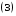 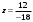 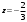 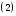 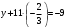 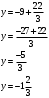 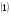 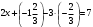 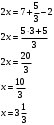 Ответ: 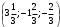 . . № 3. На прямой 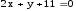 найти точку, равноудаленную от двух данных точек А(1; 1), В(3; 0). найти точку, равноудаленную от двух данных точек А(1; 1), В(3; 0).Решение: Искомую точку обозначим 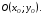 Найдём расстояния от точки О до точки А и до точки В. Найдём расстояния от точки О до точки А и до точки В.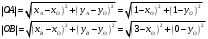 Так как точка О должна быть равноудалена от точек, то расстояния равны. 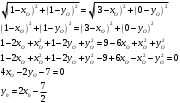 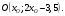 Так как точка 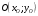 принадлежит прямой, то подставим её координаты в уравнение прямой. принадлежит прямой, то подставим её координаты в уравнение прямой.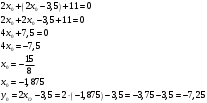 Ответ: 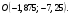 |
