Главная страница
Навигация по странице:

  • Список использованной литературы

    		•

    Системный анализ. Построим математическую модель полёта брошенного камня


    Скачать 4.24 Mb.
    НазваниеПостроим математическую модель полёта брошенного камня
    АнкорСистемный анализ
    Дата27.03.2023
    Размер4.24 Mb.
    Формат файлаdoc
    Имя файлаСистемный анализ.doc
    ТипЗакон
    #1017652

    Построим математическую модель полёта брошенного камня.

    Графическая иллюстрация рассматриваемого процесса представлена на рисунке 1

    Рисунок 1



    Необходимо разработать математическую модель движения камня, брошенного под углом к горизонту. Модель должна позволять определять координаты камня и

    его скорость в любой момент времени.

    Концептуальная постановка задачи: Определить закон движения материальной точки массой m, движущейся под действием внешних сил, если известны её начальные координаты ( x0 , y0 ), начальная скорость v0 и угол бросания a .

    Принятые гипотезы:

    · движение происходит в поле силы тяжести с постоянным ускорением свободного падения g;

    · сила сопротивления воздуха прямо пропорциональна скорости тела с коэффициентом пропорциональности k;

    · динамика объекта моделирования описывается уравнениями классической механики Ньютона;

    · скорость движения объекта моделирования много меньше скорости звука;

    · влияние ветра на движение объекта моделирования не рассматривается;

    · эффектами, вызванными собственным вращением камня вокруг центра масс, можно пренебречь;

    · земная поверхность считается плоской, а её уровень соответствует значению y = 0 .

    Для нахождения математических соотношений, описывающих рассматриваемый процесс, спроектируем уравнения второго закона Ньютона на оси неподвижной системы координат:


    Дополним полученные уравнения известными из кинематики соотношениями между скоростями и координатами:



    Начальные условия и ограничения будут иметь вид:



    Таким образом, исходная задача свелась к решению задачи Коши для следующей системы уравнений:



    Проведём анализ полученной системы уравнений. Для этого последовательно осуществим ряд проверок.

    1. Размерности правой и левой частей всех уравнений совпадают:



    2. Величины в правой части уравнения имеют схожие порядки.

    3. Характер полученных зависимостей соответствует физическому

    смыслу рассматриваемого процесса:

    · сопротивление воздуха тормозит движение во всех направлениях;

    · сила тяжести способствует уменьшению вертикальной составляющей скорости;

    · величина замедления прямо пропорциональна коэффициенту сопротивления воздуха;

    · величина замедления обратно пропорциональна массе.

    4. В пределе при k →0 (сопротивление воздуха не учитывается) получаемые зависимости имеют вид:


    Решение данной системы дифференциальных уравнений имеет вид:



    Полученные результаты совпадают с известными теоретическими положениями о характере движения тела без учёта сопротивления воздуха.

    5. Все граничные условия заданы.

    6. Существование и единственность решения задачи Коши для системы линейных дифференциальных уравнений показана теоретически.

    Таким образом, получена корректная математическая модель, описывающая рассматриваемый динамический процесс.
    Проведем исследование этой математической модели.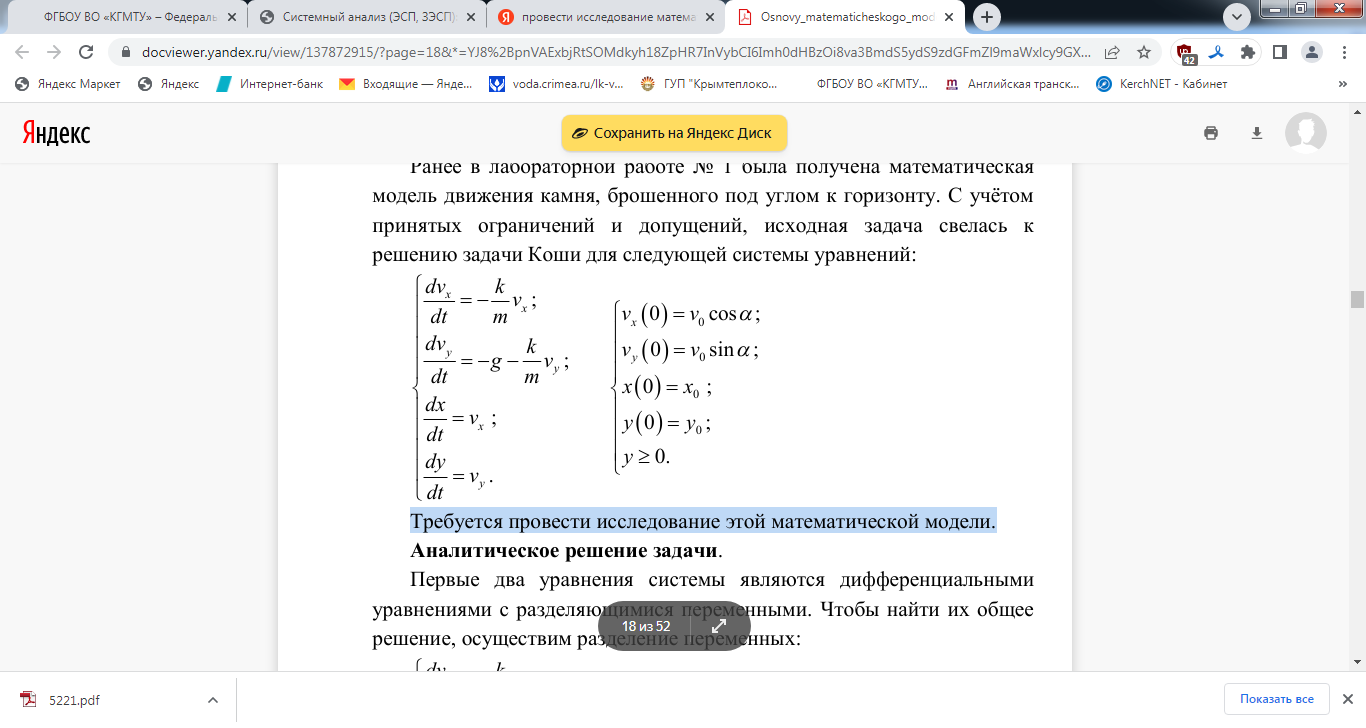



    Первые два уравнения системы являются дифференциальными уравнениями с разделяющимися переменными. Чтобы найти их общее решение, осуществим разделение переменных:



    Проинтегрируем обе части полученных уравнений:



    Здесь символами C1 и C2 обозначены некоторые константы интегрирования, конкретные значения которых определяются исходя изначальных условий.

    Выразим в явном виде уравнения для продольной и поперечной составляющих скорости:



    Определим константы интегрирования, подставив в полученные уравнения при t = 0 начальные значения скорости:


    Из полученной системы определим константы интегрирования:


    Подставив найденные значения в полученное ранее общее решение, получим:



    Подставим полученные значения в оставшиеся два уравнения исходной системы:

    Осуществим разделение переменных:



    Теперь проинтегрируем обе части полученных уравнений:


    Здесь символами C3 и C4 обозначены некоторые константы интегрирования, конкретные значения которых определяются исходя из начальных условий. Определим константы интегрирования, подставив в полученные уравнения при t = 0 начальные координаты тела:


    Из полученной системы определим константы интегрирования: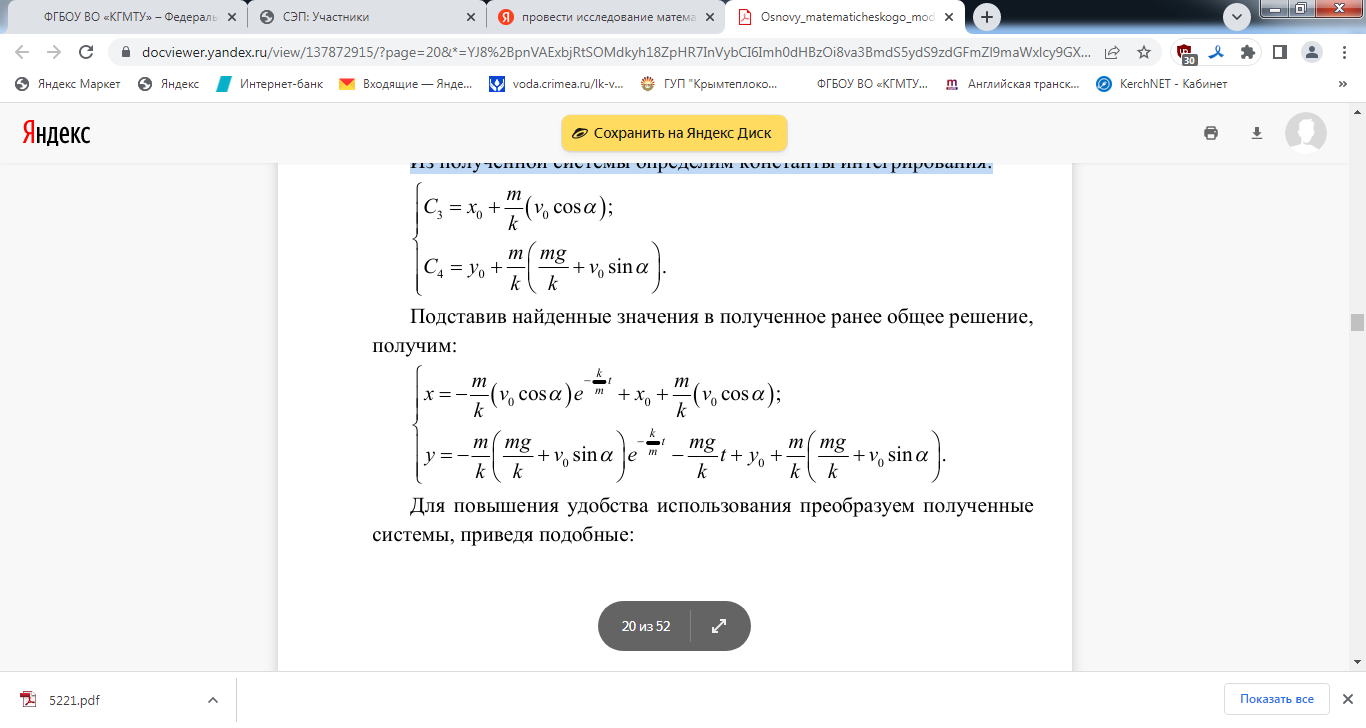



    Подставив найденные значения в полученное ранее общее решение, получим:


    Для повышения удобства использования преобразуем полученные системы, приведя подобные:



    Полученные соотношения в явном виде определяют зависимость от времени скоростей и координат движущейся материальной точки, т. е. подставляя в полученную формулу конкретное значение t, мы можем получить значение скорости и координаты в любой момент времени.
    Алгоритмическое решение задачи.

    В рассматриваемом случае применение имитационного моделирования не целесообразно, так как рассматриваемый процесс является сравнительно простым и описывается только уравнениями динамики материальной точки. Поэтому будем искать численное решение поставленной задачи с использованием методов вычислительной математики.

    Осуществим дискретизацию по времени, перейдя к рассмотрению исследуемого процесса только в некоторые фиксированные моменты времени, расстояние между которыми называется шагом дискретизации. При этом дифференциальные уравнения, описывающие динамику объекта, преобразуются в алгебраические уравнения. Воспользуемся для решения задачи Коши одним из простейших численных методов –методом Эйлера. При этом значение производной может быть приближенно заменено отношением:


    Здесь y(i) - значение функции в текущей точке, y(i +1) – значение функции в следующей точке, а величина h равна интервалу времени между двумя отсчётами и называется шагом интегрирования.
    Перейдя от дифференциальных уравнений к разностным, получим:


    Откуда в явном виде выразим значения функций в следующей точке:


    Полученные соотношения позволяют определить значения искомых функций в последующий момент времени, зная их значения в предыдущий момент времени.

    Определив аналитическое и/или алгоритмическое решение задачи, мы можем провести исследование динамики изучаемого процесса.
    Выберем для определенности следующие параметры процесса:

    1. начальная скорость 0 v =10 м/с;

    2. угол бросания a =30º;

    3. масса m =1 кг;

    4. коэффициент сопротивления воздуха k = 0,1 кг/с;

    5. начальные координаты 0 x =0, 0 y =0 (точка бросания

    располагается в начале системы координат);

    6. интервал времени между отсчётами h =0,01 с;

    7. ускорение свободного падения g =9,81 м/с2.
    Тогда формулы аналитического решения будут иметь следующий вид:


    Формулы численного решения могут быть представлены в следующем виде:


    Построим графики изменения рассматриваемых величин


    Рисунок 1 – Изменение скорости при h = 0,01 с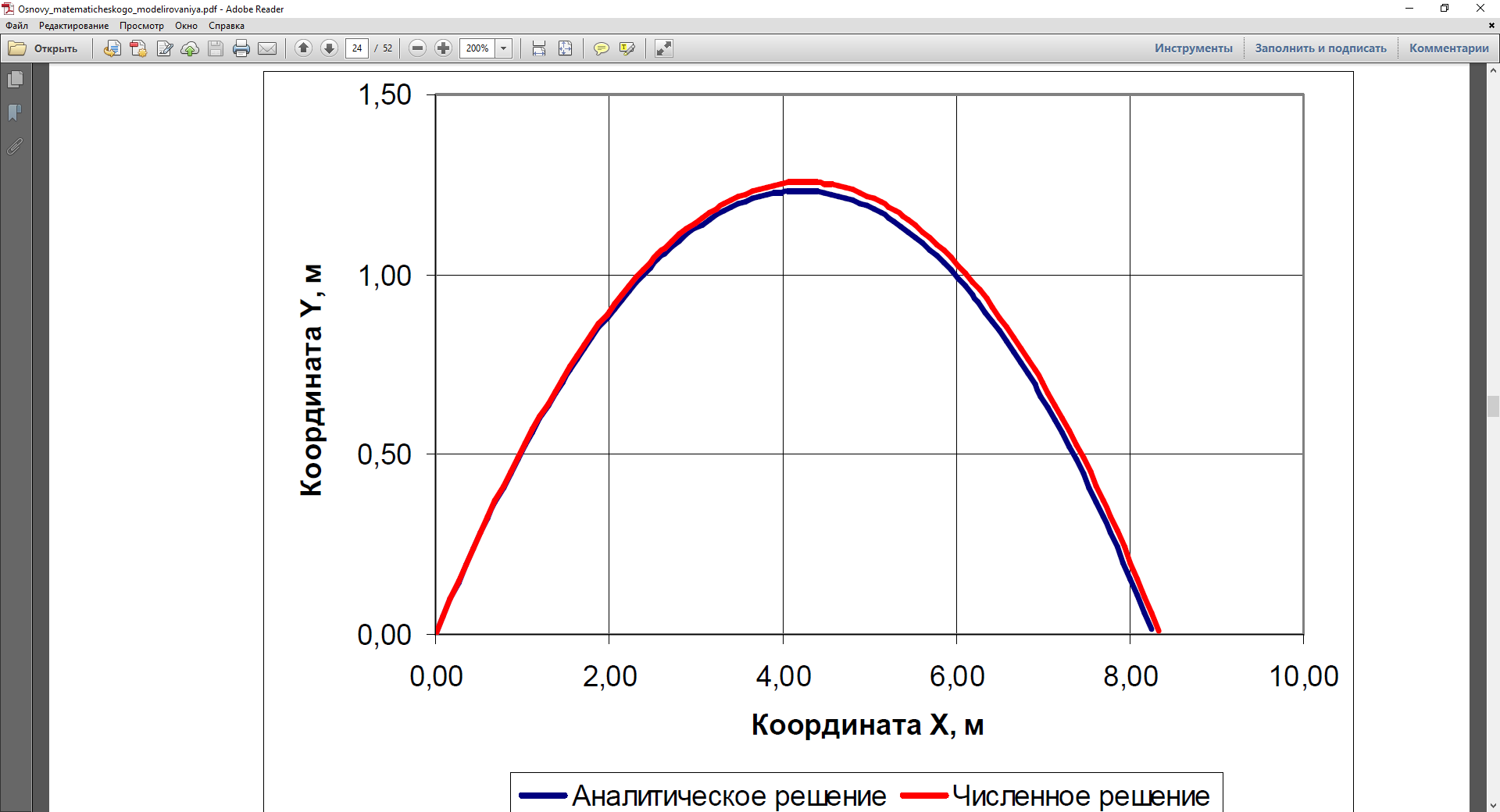



    Рисунок 2 – Траектории при h = 0,01 с
    Сравнение показывает, что графики аналитического и численного решения весьма близки друг к другу. При этом полученные результаты качественно совпадают с известными сведениями о движении тела, брошенного под углом к горизонту с малой начальной скоростью (траектория близка по своей форме к параболе). Если мы увеличим расстояние между соседними точками, и выберем величину шага h равной 0,05 с, то график аналитического решения останется прежним, а график численного решения изменится.

    На рисунке 3 показаны результаты моделирования с новым значением шага. Качественно траектории по-прежнему близки, но количественное различие между ними уже весьма существенно. Этот факт обусловлен тем, что точность численного решения зависит от выбранной величины шага – чем она меньше, тем решение точнее (и тем ближе оно к аналитическому решению).

    Рисунок 3 – Траектории при h = 0,05 с
    Для сравнения на рисунке 2.4 приведён результат моделирования при шаге 0,5 с. Показатели численного решения (дальность полёта, наибольшая высота подъёма) весьма существенно отличаются от результатов аналитического решения задачи.

    Рисунок 4 – Траектории при h = 0,5 с
    Следует отметить, что в ряде случаев некорректно выбранный шаг численного метода может привести к получению некорректных результатов: и качественно, и количественно полученные зависимости будут отличаться от аналитического решения и от реальной динамики изучаемых процессов. Более подробные сведения о численном решении систем дифференциальных уравнений содержаться в специальных разделах соответствующих дисциплин учебного плана.

    Так как форма траектории и характер зависимостей совпадает с известными теоретическими положениями и результатами экспериментов, можно утверждать, что полученная модель является адекватной.

    Исследуем зависимость получаемых решений задачи от сочетания параметров модели. Для проведения исследований будем использовать аналитическое решение задачи как более точное.

    Исследуем, как зависит траектория движения от угла бросания. На рисунке 5 показаны графики для трёх значений угла a =30º, a =45º, a =60º. Результаты моделирования соответствуют известному теоретическому положению о том, что наибольшая дальность полёта брошенного тела достигается при угле бросания 45º.


    Рисунок 5 – Траектории при различных углах бросания.
    Исследуем, как зависит траектория от других параметров. На рисунке 6 показаны графики для трёх значений массы m=0,1 кг, m=1 кг, m=10 кг. Результаты моделирования соответствуют известным сведениям из практики о том, что чем больше масса тела при

    неизменной начальной скорости и угле бросания, тем дальше оно улетит.

    На рисунке 7 показаны графики для трёх значений коэффициента сопротивления k = 0,01 кг/с; k = 0,1 кг/с; k = 1 кг/с. Результаты моделирования также соответствуют известным сведениям из практики и теоретическим положениям (чем выше сопротивление среды, тем меньше дальность и высота полёта)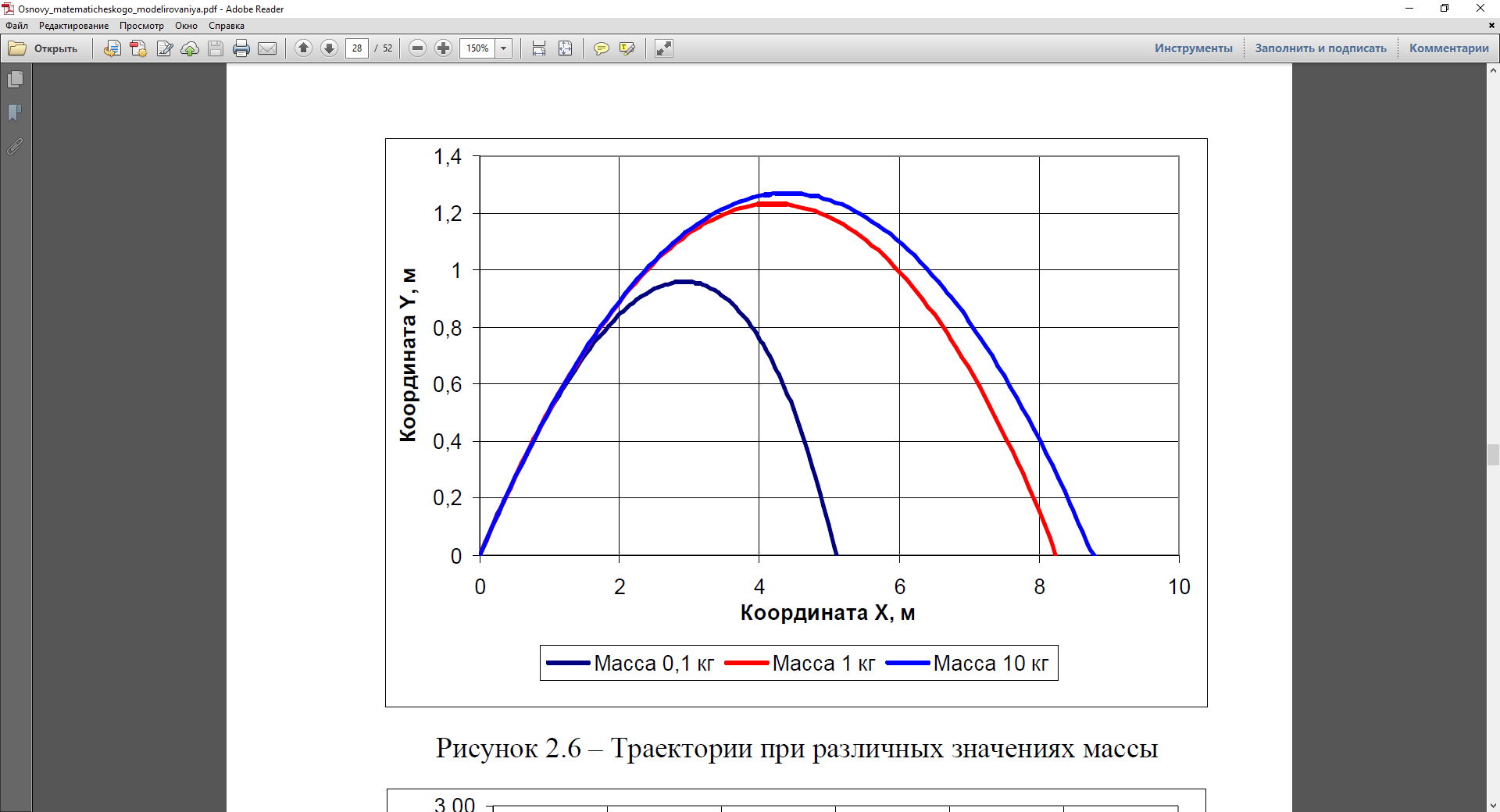


    Рисунок 6 – Траектории при различных значениях массы


    Рисунок 7 – Траектории при различных значениях k
    Таким образом, сформированная математическая модель может быть использована для прогнозирования динамики исследуемого процесса при интересующих нас сочетаниях параметров, а также для оптимизации параметров с целью достижения требуемых показателей (например, подбор оптимального угла бросания для попадания в заданную точку при наличии ограничения по максимальной высоте).

    Список использованной литературы

    1. Берталанфи Л. Фон. Общая теория систем: критический обзор / Берталанфи Л. Фон // Исследования по общей теории систем. – М. : Прогресс, 2009. – С. 23 – 82.

    2. Вдовин, В.М. Теория систем и системный анализ : учебник / В.М. Вдовин, Л.Е. Суркова, В.А. Валентинов. — 3-е изд. — Москва : Дашков и К, 2016. — 644 с. — ISBN 978-5-394-02139-8. — Текст : электронный // Электронно-библиотечная система «Лань» : [сайт]. — URL: https://e.lanbook.com/book/93352 .

    3. Волкова В.Н., Денисов А.А. Основы теории систем и системного анализа. - СПб : "СПбГТУ", 2001.-370 с.

    4. Волкова, В.Н. Системный анализ информационных комплексов : учебное пособие / В.Н. Волкова. — 2-е изд., стер. — Санкт-Петербург : Лань, 2016. — 336 с. — ISBN 978-5-8114-2291-3. — Текст : электронный // Электронно-библиотечная система «Лань» : [сайт]. — URL: https://e.lanbook.com/book/75506 .

    написать администратору сайта