ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ ПО СТАТИСТИЧЕСКИМ ДАННЫМ. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ. Практическая работа 2 Определение показателей безотказности невосстанавливаемых объектов по статистическим данным

• Название: Практическая работа 2 Определение показателей безотказности невосстанавливаемых объектов по статистическим данным
• Анкор: ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ ПО СТАТИСТИЧЕСКИМ ДАННЫМ
• Дата: 25.04.2023
• Размер: 87.03 Kb.
• Имя файла: ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ.docx
• Тип: Практическая работа; #1087457

<sub>Практическая работа № 2

«Определение показателей безотказности

невосстанавливаемых объектов

по статистическим данным»</sub>

Цель работы:

1. 
   Закрепить теоретические знания, полученные в разделе «Единичные показатели надежности» по вопросу «Показатели безотказности».
   
2. 
   Освоить методику определения показателей безотказности по статистическим данным о надежности неремонтируемых изделий на определенном промежутке времени.
   
3. 
   Получить практические навыки построения и анализа зависимостей показателей безотказности во времени
   

1. 
   МЕТОДИКА определения показателей безотказности на определенном промежутке времени
   

На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.

Показатели безотказности определяются для каждого интервала в следующей последовательности:

1. 
   Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле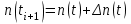
   

(2.1)

2. 
   Определяем количество работоспособных изделий 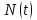на конец каждого периода по формуле
   

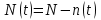, (2.2)

где n(t) – количество отказавших изделий на конец рассматриваемого периода за период от 0 до t.

3. 
   Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле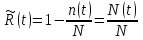
   

. (2.3)

4. 
   Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле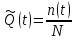
   

. (2.4)

5. 
   Определяем статистическую оценку плотности вероятности отказов по формуле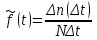
   

, (2.5)

где Δn(Δt) – количество отказавших изделий в данном временном интервале Δt.

6. 
   Определяем значение интенсивности отказов по формуле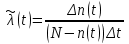
   

, (2.6)

2. 
   ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
   

1. 
   Изучить методику расчёта показателей безотказности за определенный промежуток времени
   
2. 
   Проанализировать условия задачи и определить исходные данные для расчета показателей безотказности
   
3. 
   Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.
   
4. 
   Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.
   
5. 
   Результаты расчета отразить на графиках.
   
6. 
   Ответить на контрольные вопросы.
   

3. 
   Оформление результатов работы
   

Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 1000 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 2.1.

Задание:

1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.

2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

3. Результаты расчета отразить на графиках.

Решение.

1. 
   Согласно условию задачи длина рассматриваемых периодов Δt равна 100 часам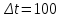
   

час.

2. 
   В начальный период времени изделия должны находиться в работоспособном состоянии и количество отказавших изделий на время t=0 равно 0, следовательно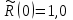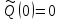
   

.

.

3. 
   Определяем количество работоспособных изделий на конец первого периода по формуле (2.2)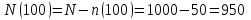
   

шт.

4. 
   Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле (2.3)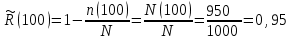
   

.

5. 
   Определяем количество отказавших деталей нарастающим итогом на конец первого периода по формуле (2.1)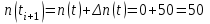
   

6. 
   Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле (2.4)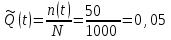
   

.

7. 
   Определяем статистическую оценку плотности вероятности отказов по формуле (2.5)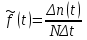
   

.

8. 
   Определяем значение интенсивности отказов по формуле (2.6)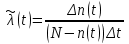
   

9. 
   Аналогично проводим расчеты для всех остальных периодов и результаты расчета для удобства сводим в таблицу 2.1
   

Таблица 2.1 – Результаты расчета статистических оценок показателей безотказности

Временной интервал Δt, час	Количество отказов за данный интервал Δn(t)	Количество работоспособных изделий на конец периода N(t)	Количество отказавших изделий на конец периода n(t)	Вероятность безотказной работы R(t)	Вероятность отказа Q(t)	Плотность вероятности отказов f(t), ·10-2	Интенсивность отказов λ(t), ·10-2
		2406
0 – 100	36	2370	36	0,985	0,015	0,00015	0,00015190
100 – 200	45	2325	81	0,966	0,034	0,00019	0,00019355
200 – 300	90	2235	171	0,929	0,071	0,00037	0,00040269
300 – 400	590	1645	761	0,684	0,316	0,00245	0,00368663
400 – 500	339	1306	1100	0,543	0,457	0,00141	0,00259571
500 – 600	392	914	1492	0,380	0,620	0,00163	0,00428884
600 – 700	396	518	1888	0,215	0,785	0,00165	0,00764479
700 – 800	90	428	1978	0,178	0,822	0,00037	0,00210280
800 – 900	92	336	2070	0,140	0,860	0,00038	0,00273810
900 – 1000	55	281	2125	0,117	0,883	0,00023	0,00195730

10. 
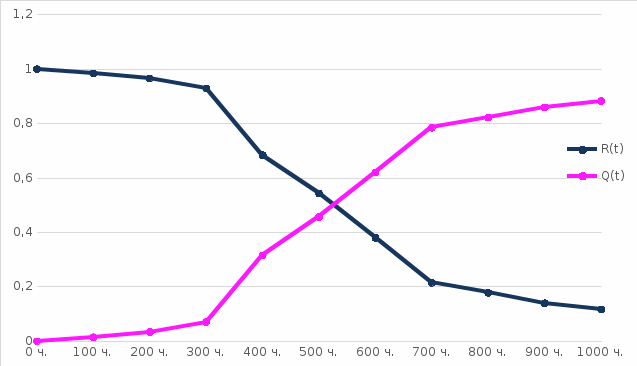
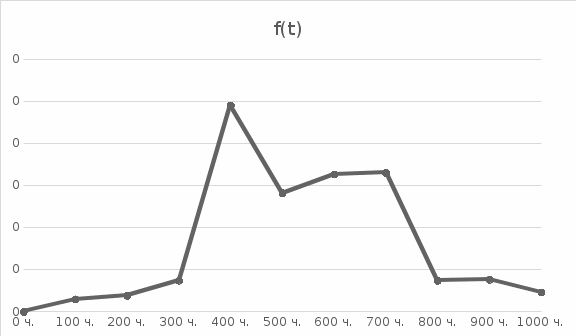
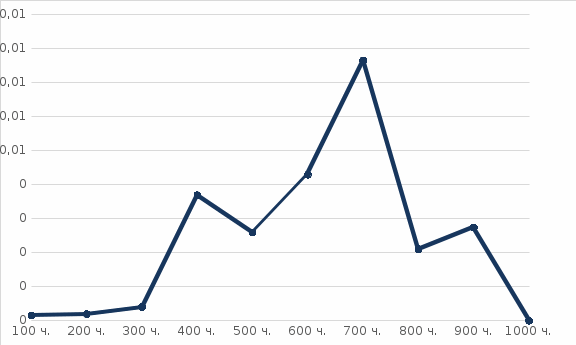
    По данным расчета строим графики зависимости расчетных величин по времени (рисунки 2.1, 2.2, 2.3)
    

Рисунок 2.1 – График зависимости вероятности безотказной работы и вероятности отказа от времени

Время, t

Интенсивность отказов

Рисунок 2.2 – График зависимости плотности распределения отказов во времени

Рисунок 2.3 – График зависимости интенсивности отказов от времени

4. 
   
   

4. 
   Задания для самостоятельной работы
   

Исходные данные: На испытание поставлено N изделий. Испытания проводятся в течение 1000 часов. Результаты испытаний представлены в таблице 2.2.

Задание:

1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.

2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

3. Результаты расчета отразить на графиках.
Таблица 2.2 – Исходные данные для выполнения домашнего задания по практической работе № 2

Номер варианта	Общее кол-во изделий	Количество отказавших изделий за интервал времени ti, шт.
		0 – 100	100 – 200	200 – 300	300 – 400	400 – 500	500 – 600	600 – 700	700 – 800	800 – 900	900 – 1000
1	3007	49	99	88	554	594	542	580	86	87	40
2	2379	68	41	37	434	501	282	471	74	77	99
3	2754	75	97	65	554	305	410	407	83	96	82
4	2415	67	56	81	346	405	442	490	57	35	60
5	2785	51	89	98	383	497	575	501	35	92	60
6	2303	63	73	94	263	261	493	484	52	64	87
7	2430	44	62	44	299	482	362	436	49	84	68
8	2337	99	44	75	299	575	411	217	36	46	55
9	2217	66	43	57	395	218	355	510	67	90	58
10	1940	61	66	71	232	376	226	305	72	37	81
11	1913	60	50	100	259	363	438	250	58	58	73
12	2511	72	84	100	377	533	374	520	75	52	44
13	2460	40	94	40	363	426	541	435	86	83	47
14	2306	35	80	37	318	575	387	493	54	35	37
15	1919	37	35	80	340	374	403	215	77	58	96
16	2406	36	45	90	590	339	392	396	90	92	55
17	2654	47	68	77	326	584	470	570	62	74	70
18	2581	83	52	93	431	303	567	345	93	81	89
19	2554	51	48	58	432	218	595	353	99	89	63
20	2626	65	99	73	591	220	550	544	47	60	88

5. 
   Контрольные вопросы:
   

1. 
   Свойства функции вероятности безотказной работы?
   
2. 
   Свойства функции вероятности отказа?
   
3. 
   Каким образом определяется плотность распределения наработки во времени?
   
4. 
   Кривая зависимости интенсивности отказа во времени.
   
5. 
   Кривая плотности распределения отказов во времени.
   

Ответы:

1. Функция вероятности безотказной работы имеет следующие свойства:

- P(0) = 1, то есть вероятность отсутствия отказов в начальный момент времени равна 1.

- 0 ≤ P(t) ≤ 1 для любого t, то есть вероятность безотказной работы всегда находится в диапазоне от 0 до 1.

- P(t) убывает при увеличении времени, что означает, что вероятность безотказной работы уменьшается с течением времени.

- P(∞) = lim P(t) = 0, то есть вероятность безотказной работы стремится к 0 при бесконечном времени работы системы.

2. Функция вероятности отказа имеет следующие свойства:

- Q(0) = 0, то есть вероятность отказа в начальный момент времени равна 0.

- 0 ≤ Q(t) ≤ 1 для любого t, то есть вероятность отказа всегда находится в диапазоне от 0 до 1.

- Q(t) возрастает при увеличении времени, что означает, что вероятность отказа увеличивается с течением времени.

- Q(∞) = lim Q(t) = 1, то есть вероятность отказа стремится к 1 при бесконечном времени работы системы.

3. Плотность распределения наработки во времени определяется как отношение вероятности отказа в момент времени t к интенсивности отказов в момент времени t: f(t) = Q(t) / λ(t). Таким образом, плотность распределения наработки во времени описывает вероятность возникновения отказа в определенный момент времени при заданной скорости отказов.

4. Кривая зависимости интенсивности отказа во времени может иметь различные формы в зависимости от типа системы и ее эксплуатационных условий. Одним из часто встречающихся видов кривой является кривая "модели износа", которая представляет собой увеличивающуюся во времени кривую, отражающую рост интенсивности отказов с увеличением наработки системы.

5. Кривая плотности распределения отказов во времени также может иметь различные формы в зависимости от типа системы и ее эксплуатационных условий. Одним из часто встречающихся видов кривой является кривая "экспоненциального распределения", которая представляет собой убывающую во времени кривую плотности распределения, отражающую вероятность отказа в последующий момент времени при заданной вероятности отказа в текущий момент времени.