Практическая работа 5 Центр тяжести

• Название: Практическая работа 5 Центр тяжести
• Дата: 12.01.2022
• Размер: 0.65 Mb.
• Имя файла: _prakticheskaya_rabota_no5.doc
• Тип: Практическая работа; #329446

Камина В.Н.

Практическая работа №5
Центр тяжести.
Иметь представление о системе параллельных сил и центре системы параллельных сил, о силе тяжести и центре тяжести.

Знать методы для определения центра тяжести тела и формулы для определения положения центра тяжести плоских фигур.

Уметь определять положение центра тяжести простых геометрических фигур, составленных из стандартных профилей.
Сила тяжести.
Сила тяжести – равнодействующая сил притяжения к Земле, распределенных по всему объёму тела. Силы притяжения, приложенные к частицам твердого тело, образуют систему сил, линии действия которых сходятся в центре Земли (рис.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.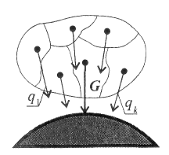



Рис.1.
Точка приложения силы тяжести.
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.

Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис.2).

Тело состоит из частей, силы тяжести которых g_k приложены в центрах тяжести (ЦТ) этих частей.

Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центра С.

x_C , y_C и z_C – координаты центра тяжести С.

x_k, y_k и z_k – координаты центров тяжести частей тела.

Из теоремы Вариньона следует:



Рис.2.

В однородном теле сила тяжести пропорциональна объёму V:

G = γV;

где -γ вес единицы объёма.

Следовательно, в формулах для однородных тел: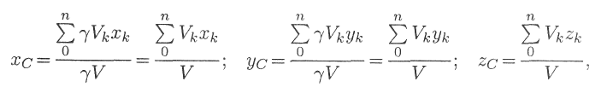



где – V_k – объем элемента тела; V – объём всего тела.
Центр тяжести однородных плоских тел

(плоских фигур).

Очень часто приходится определить центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать : V = Ah, где А – площадь фигуры, h – ее высота.

Тогда после подстановки в записанные выше формулы получим: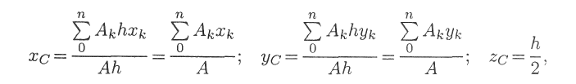



где A_k – площадь части сечения; x_k , y_k – координаты ЦТ частей сечения.

Выражение называют статическим моментом площади (S_y).

Координаты центра тяжести сечения можно выразить через статический момент:



Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.

Определение координат центра тяжести

плоских фигур.
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис.3: а) – круг; б) – квадрат, прямоугольник; в) – треугольник; г) – полукруг).


Рис.3.

Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.

Центр тяжести стержня находится на середине высоты.

При решении задач используются следующие методы:

1. 
   метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
   
2. 
   метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
   
3. 
   метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
   

Примеры решения задач.

Пример 1. Определить положение центра тяжести фигур,

представленной на рис. 4.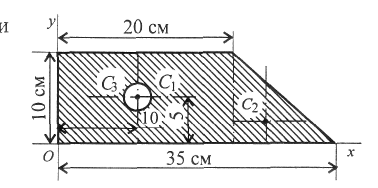


Рис.4.

Решение
Разбиваем фигуру на три части:

1 – прямоугольник, А₁ = 10·20 = 200см²;

2 – треугольник, А₂ = 1/2·10·15 = 75см²;

3 – круг, А₃ =π R²; A₃ = 3,14·3² = 28,3см².

ЦТ фигуры 1: x₁ = 10cм; y₁ = 5см.

ЦТ фигуры 2: х₂ = 20 + 1/3·15 = 25см; у₂ = 1/310 = 3,3см.

ЦТ фигуры 3: х₃ = 10см; у₃ = 5см;

x_C = [200·10 + 75·25 – 28,3·10] : [200 + 75 – 28,3] = 14,5см.

Аналогично определяется у_C = 4,5см.
Пример 2. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис.5).

Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.

Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих справочниках.



Рис. 5.
Решение
I. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:

1 – швеллер №10 (ГОСТ 8240 – 89); высота h = 100мм; ширина полки b = 46мм; площадь сечения А₁ = 10,9см²;

2 – двутавр №16 (ГОСТ 8239 – 89); высота 160мм; ширина полки 81мм; площадь сечения А₂ = 20,2см²;

3 – лист 5×100; толщина 5мм; ширина 100мм; площадь сечения

А₃ = 0,5·10 = 5см².

II. Координаты центров тяжести каждой фигуры можно определить по чертежу.

Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата x_C = 0

Швеллер 1: у₁ = а + h₂ + z_o; y₁ = 0,5 + 16 + 1,44 = 17,54см.

Двутавр 2: у₁ = а + h₂/2; y₂ = 0,5 + 16/2 = 8,5см.

Лист 3: у₃ = а/2 = 0,25см.

III. Определение центра тяжести составного сечения:
y_C = [A1y1+ A2y2 + А3у3] : [A1 + A2 + A3],
y_C = [10,9·17,5 + 20,2·8,5 + 5·0,25] : [10,9 + 20,2 + 5] = 10см.
Практическое занятие

Центр тяжести.
Знать методы определения центра тяжести тела и плоских сечений, формулы для определения положения ЦТ плоских сечений.

Уметь определять положение центра тяжести сложных геометрических фигур, определять положения центра тяжести фигуры, составленных из стандартных профилей.
Основные формулы и предпосылки расчета.
Центры тяжести простейших сечений (рис.6).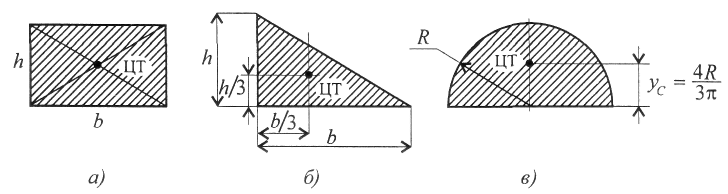



Рис.6

Геометрические характеристики стандартных прокатных профилей в Приложении

Методы расчета:

1. 
   метод симметрии;
   
2. 
   метод разделения на простые части;
   
3. 
   метод отрицательных площадей.
   

Координаты центров тяжести сложных и составных сечений: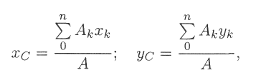


где А – площади частей сечения х; у – координаты ЦТ частей сечения; А – суммарная площадь сечения,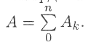
Упражнения при подготовке к самостоятельной работе.

1. 
   Определить положение центра тяжести каждой из фигур, составляющих сечение (рис. 7). Размеры на чертеже указаны в мм.
   
2. 
   Определить координату х изображенного сечения (рис.8).
   

Замечание. Сечение расчленить на три части.



Рис.7. Рис.8.

3. 
   Сколько координат центра тяжести нужно определить расчетным путем для каждого из изображенных сечений (рис.9)?
   
4. 
   По таблицам ГОСТ определить необходимые параметры сечений (рис.10).
   

Рис.9. Рис.10.

5. 
   Определить координату у фигуры (рис.10).
   
6. 
   Какая характеристика сечения определяется по указанной формуле?
   

Расчетно – графическая работа.
Задание 1. Определить координаты центра тяжести заданного сечения.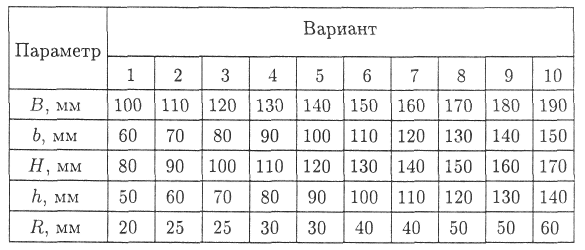




Задание 2. Определить координаты центра тяжести составного сечения. Сечения состоят из листов с поперечным размерами а х б и прокатных профилей по ГОСТ 8239-89, и ГОСТ 8509-86. Уголок выбирается наименьшей толщины.

Размеры стандартных профилей в Приложении .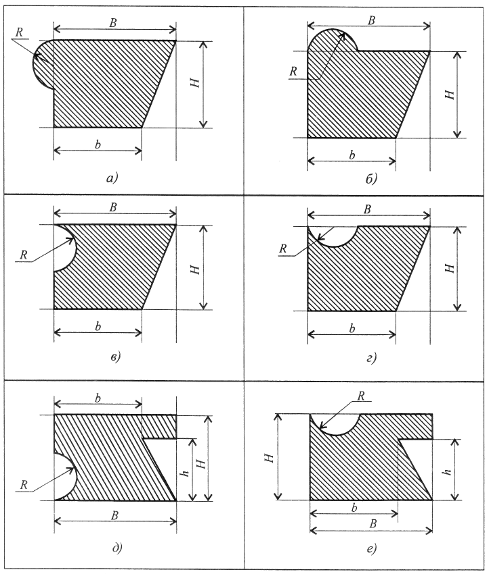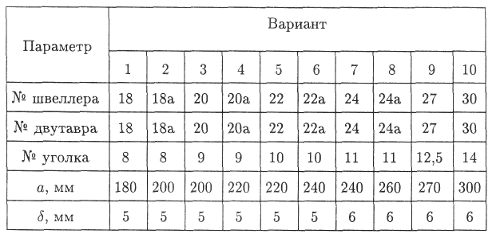





При защите работ ответить на вопросы тестового задания.


2013